Духин А.А. Теория информации
Подождите немного. Документ загружается.


61
§ 2.
ТЕОРЕМЫ
ШЕННОНА
ЛАЯ
ИСТОЧНИКОВ
БЕЗ
ПАМЯТИ
ВТОРАЯ
ТЕОРЕМА
ШЕННОНА.
Для
класса МДА) высоковероятностных
по-
следовательностей, реализованных
на
источ-
нике
без
памяти [A,p(S)], определяемого
за-
данным уровнем
а,
(0
<а
<
1),
имеет место
/
0
G|M,(G)l
l
l
Z
}
еН
~
(2-2.8)
где
Нда
=
-y^PjfogPj
-
энтропия источника.
Доказательство.
В
зависимости
от
величины
р(с^)
класс
С/
разделим
на
три
подкласса:
Q = Kj +
К2
+К3
следующим образом:
К,={с,:р(с
/
)*а-<<
Н
«-
|
1>},
(2-2.9)
где
а
>
1
-
основание логарифмов,
т] > 0
-
постоянная, фигурирующая
в
формулировке первой теоремы
Шеннона (2.2.1).
с, :а^<
Н
-^> <р(с,)<а^
(Н
-^
)
}, (2.2.10)
с,:р(с,)<а^
Н
-^}.
Согласно такому разбиению множества всех последовательностей
К
2
=С'Д
а К, иК
3
=С". Следовательно, при
£
-»оо
суммарная вероятность
последовательностей, вошедших
в
первый
и
третий классы, стремится
к
нулю:
(
\
К
?
=
К
3
=
Ит
I Р(<^) +
ZP(C^)
=
0.
Значит,
в
класс
МДа)
войдут последовательности
из Kj и,
частично,
из К
2
.
Первую последовательность
из К
2
, не
вошедшую
в
МДа), обозначим
сДа).
Приведём ряд очевидных неравенств:
|МДа)|а^
(Ноо+Т1)
< Ер(с^)<а + р(сДа))<а +
а^
(Ноо
~
Т1)
.
М^(а)
Отсюда получаем:
log\M
f
(a)\
JOGG
+
a-^-^)
<
* .
'4-HEN
+Т|.
1
См.
следствие
из
первой
теоремы
Шеннона.

62
ГЛАВА
П.
ИСТОЧНИКИ
СООБЩЕНИЙ
Устремляя £
->
СЮ,
г| -> 0, получаем:
log\MAa)\
п
lim sup—
х
—
^йИ».
(2.2.11)
Г)->00
Имеет место неравенство:
iM^A^^^^A-P^,),
(2.2.12)
где PCKj) обозначает суммарную вероятность всех
последовательностей
из
класса
К
г
.
Из (2.2.12) получаем:
1о
§
\М
е
(а)\^1о
ё
{а-¥(К
г
))
in
£
£
00 Ь
Устремляя £
-*
со,
т]
-> 0, получаем:
/t'
nM
V^
H
-
(2213)
Из неравенств (2.2.11)
и
(2.2.13) получаем доказательство теоремы 2.2.2.
А
Приведём носящую приближённый характер геометрическую интерпрета-
цию распределения вероятностей
на
множестве реализаций
С
е
источника без
памяти. Вероятности последовательностей
с
е
е С
£
расположим
по
убыванию
их величины
и
занумеруем натуральными числами
от 1 до к/. В
класс
Kj
войдут
все
последовательности
с
аномально повышенными вероятностями.
Так
как К
2
= , то
класс
К
2
образован последовательностями, имеющими
примерно одинаковые вероятности (р(с
Г
£)~а~"
ш
°°), удовлетворяющими
закону больших чисел. Класс МДа) составлен
из
всех последовательностей
К
г
и,
частично,
из
последовательностей
К
2
.
Подавляющее число последова-
тельностей, составляющих класс
К
3
,
имеет аномально малые вероятности.

63
§
2.
ТЕОРЕМЫ
ШЕННОНА
ДЛЯ
ИСТОЧНИКОВ
БЕЗ
ПАМЯТИ
4
P(c
f
)
'л
N
Рис.
2.1.
Распределение вероятностей реализаций источника
[А,р($)]
2
Информационная устойчивость, которой обладают последовательности
cJeC',,
означает,
что
собственная информация
для
любой последовательнос-
ти
из
этого класса есть величина постоянная.
Это же
свойство можно трак-
товать
как
свойство равнораспределённости,
то
есть вероятности последова-
тельностей
из
класса
С\
приближенно равны а~
н
°°*. Отсюда получаем
|С',|
=
а
н
^
Из второй теоремы Шеннона (2.2.8) также следует,
что
|МДа)|
= а
Но0
^.
Следовательно, число высоко вероятных последовательностей, вошедших
в
класс
Kj,
пренебрежимо мало
по
сравнению
с |К
2
| или
|МДа)|.
В
то
же
время имеет место:
Um
Щ=1ш
P\=lim
= Вт
.<№<>•**•>.
Так
как <
logn, причём равенство возможно только
при
равномерном
распределении
на А, то
искомый предел равен нулю. Число последователь-
ностей, удовлетворяющих (2.2.4), исчезающе мало
по
сравнению
с
общим
числом последовательностей.
Пример
2.1.
Рассмотрим источник
без
памяти
[A,p(s)j
следующего вида:
А
=
{0Д},
р(0)
=
р(1)Л.
Положим основание логарифмов
а = 2.
2
Для
удобства
восприятия масштаб
по
оси
ординат
и
участок
на
оси
абсцисс,
соответствующий
классам
^ и К
2
,
искусственно
увеличены.
64
ГЛАВА
II. Источники
СООБЩЕНИЙ
Тогда н = -
Источник порождает двоичные последовательности:
=(б
Ь
...,вг),
е>=0,1;
р(с^) = ^.
2
Для т|>0 для любой последовательности с^еС^ выполняется:
2-«
н
«
+т
»<р(с^)<2^
(Н
^
л)
1
то есть С, = С,, С? = 0.
Пример 2.2. Рассмотрим источник без памяти [A,p(s)j следующего вида:
A
= {o,l},
p(0)
= q,
р(1)
=
р,
p + q
= l, р£0, q^O.
Пусть в последовательности е С
е
имеется т
0
нулей и т
2
единиц; т
0
+ т, = £
у
пусть 5>0. Тогда, согласно (2.2.4), в класс
С\ войдут те последовательности, для которых
Imi
т
0
<8,
<8.
Приведённые неравенства означают, что С\ состоит из последовательнос-
тей, абсолютные частоты появления букв в которых находятся в 8-окрестнос-
ти математического ожидания.
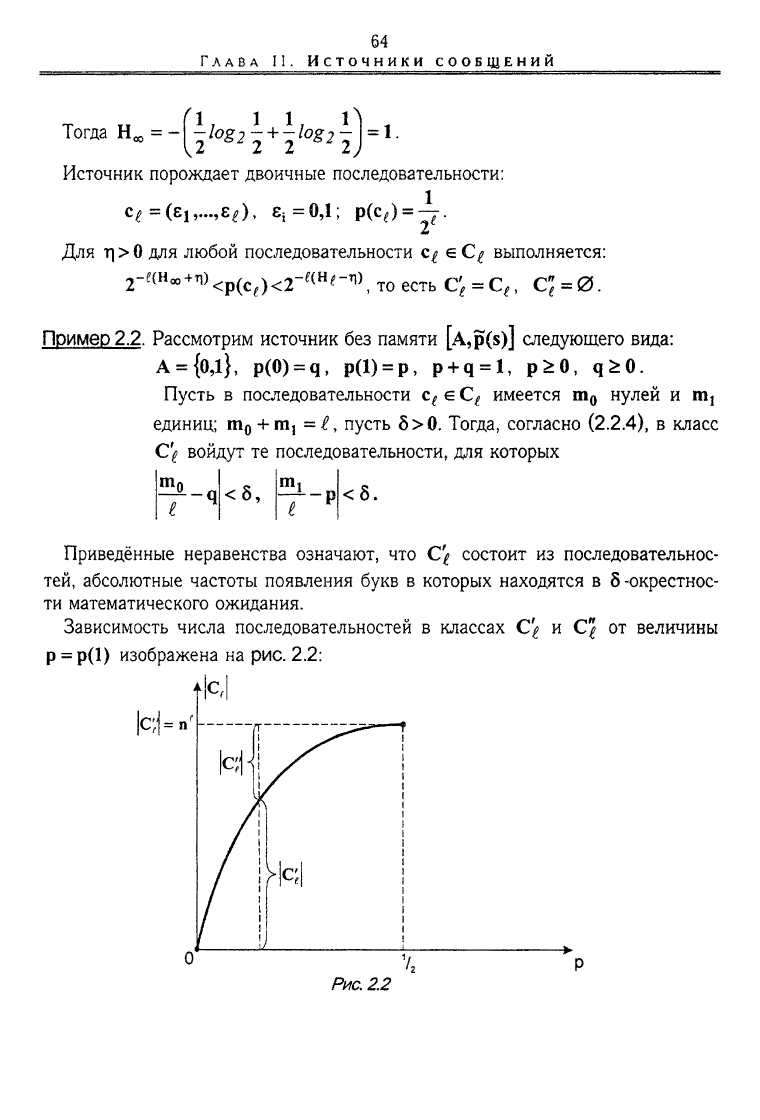
Зависимость числа последовательностей в классах С'^ и CJ от величины
р = р(1) изображена на рис. 2.2:
Рис.
2.2

§3
Результаты, полученные в предыдущем параграфе, распространяются на
марковские источники, в том числе и на марковские источники порядка т.
Определение
3.1.
Дискретный стационарный источник
[A,p(s)] называется марковским
источником порядка т, если для любого
£(£
2*
ш) и любой последовательности
с( = (а^ ,...,а;^) выполняется:
p(
a
i^
/
a
i^i v^ajj )= р(а^ /а^
,...,а^_
т+1
).
(2.3.1)
Из определения следует, что последовательности {с^} являются реализа-
циями конечной стационарной цепи Маркова с глубиной зависимости т. Ни-
же будем предполагать, что цепь Маркова неразложимая и ациклическая.
Определение
3.2.
Величина
Н
(Ю
=
_ y
p
(a
ll1M
.,a
ik
)tog p(a
ik
/а^^а^)
1
{cr}
называется шаговой энтропией мар-
ковского источника порядкак.
(2.3.2)
Определение
3.3.
Величина
Н
к
=-J-Ур(а|,,...,а|
к
)^ p(a
ilV
..,a
ik
)
называется энтропией источника на\
один знак.
(2.3.3)
Рассмотрим соотношение:
р(
а
ч >~>Ч )
=
р(
а
и )p(
a
i
2
/a
h )p(
a
i
3
7
^2
a
ii
) P(
a
ik
/a
ik-i '->
а
ч )•
1
Здесь и ниже символ означает, что суммирование проводится по всем последователь-
{с
к
}
ностям 6 •
МАРКОВСКИЕ ИСТОЧНИКИ

66
ГЛАВА
11. И ст
очники
СООБЩЕНИЙ
Логарифмируя
его,
усредняя
по
множеству
{С
к
},
умножая
на -
—,
полу-
к
чаем связь шаговой энтропии
и
энтропии
"на
знак":
Н
к
= ~~ Е
P(
a
ij
,-,а
1к
)
togp^,,)-
i У
рСа^
,...,a
ik
)fogp(a,
2
/а^
) -
-™
,1
P(
a
ii
^a
ik
)/agp(a
ik
/a
ik t
,...,
а|1
£H
(|)
.
R
{c
k
}
k
i=l
Покажем,
что
последовательность
H
(k)
k = l, 2,.,.
является невозрастаю-
щей,
то
есть для любого
к € N
Н*
к+1)
^ Н
(к)
.
Действительно:
Н
(к+,)
=-Vp(a
llf
.^a
lk+1
)fogp(a
lk+1
/а,
к
,...,а
и
)
=
=
H
(
a
i
k+
1
'
a
i
k
-
a
i! H(a
ik+1
/a
iR
,...a
l2
н(а
1к
/а
1м
„.л^
) = Н<
к
>
Последовательность
Н
к
также является невозрастающей:
к
к+1
<к
+
1)Хн<
!
>-кХн<'>
Н
к
- Н
к+1
= Ы И =
-J_V(
Н
('>
-
Н
(К+1)
Ъ:
0.
к
к 1
к(к
+
1) k(k
+
l)~
v
'
Определение 3.4.
Величина
lim Н
(к)
= Н
к
= > 0 -
назы-
к-¥со к-¥<в
вается энтропией марковского источника.
(2.3.4)
Первый предел существует
в
силу теоремы Вейерштрасса, второй
- как
сред-
нее арифметическое членов последовательности
{н
(к>
},
имеющей конечный
предел.
В проведённых рассуждениях зависимость марковского типа могла рас-
пространяться
на
произвольную глубину
т.
Рассмотрим некоторые частные
случаи.
m
- 0.
Зависимость между отдельными знаками отсутствует. Марковский
ис-
точник является источником
без
памяти.
Н
(к)
=
Н
к
= Н, = , где Я
х
= - £
Pi
log
Pl
.
i=l
т
= 1.
Появление очередного знака
в
последовательности зависит
от
предыду-
щего знака.
Н
(к)
=
Н
(2
\ при к>2.

67
§ 3. МАРКОВСКИЕ
ИСТОЧНИКИ
lim
Н
(к)
=
Н
(2)
=
Н
00
=- У p(a
iiai2
)togp(a
l2
/aj.
{С
2
}
Энтропия на знак для этого случая представляется выражением:
Н
к
=-[н
(1)
+(к-1)Н
(2)
]. lim =
Пусть зависимость между знаками в последовательностях
{с^
}
распростра-
няется на глубину т. Тогда Н
(к)
= Н*
т
\ при к>т.
(2.3.5)
lim Н
(к)
= Н<"" = Н
да
=
к ->•«>
,{т)_
- I р(ч, ' ~'
а
*т
Kp(
a
im
/a
im-l '-'
а
Ч )
{Сщ}
Hk=-
т-1
]Гн
(0
+(к--т
+ 1)Н
(т)
. lim Нь = Н
(т)
= Н
а
Рассмотрим источник сообщений
[A,p(s)J,
порождающий символы алфави-
та А согласно простой, стационарной и эргодической цепи Маркова с конеч-
ным числом состояний. Обозначим так же, как и в § 2, посредством - {с^}
совокупность всевозможных последовательностей длины £, порождённых
этим источником.
Теорема 3.1 (Первая теорема Шеннона для марковских источников порядка
m = 1). Для любых е >
О,
> 0 существует £
0
такое, что
при £>£
0
все реализации длины £ источника [A,p(s)j
могут быть разбиты на два класса:
=
С
^
-1-
с ^.
Для любой последовательности с'
£
е С\ имеет место:
I
I
II,
1
|
<Т
Ь (2.3.6)
Jog
Н
0
где H
w
= -
Тр,р
ц
fog
р
ц
=-Ур(ц)
log р
ц
- энтропия ис-
точника сообщений.
Суммарная вероятность последовательностей из класса
С" меньше е.
Доказательство.
1°.
Зададимся произвольными е>0, т|>0. Множество всевозможных после-
довательностей С^,. порождённых рассматриваемым источником, разделим

68
ГЛАВА
II. Источники
СООБЩЕНИЙ
на два класса. Отнесём к первому классу С\ те и только те последователь-
ности, для которых выполнено неравенство:
!
m
u - ^PiPtjj <*8, У =
1,...,п,
(2.3.7)
где - абсолютная частота встречаемости биграммы (а
4
ар. Ко второму
классу С" отнесём все последовательности, для которых неравенство
(2.3.7) не выполнено, по крайней мере, для одной пары (ij).
Условие (2.3.7) равносильно выполнению системы неравенств:
^PiPij
™
^<п1ц<Ф*Ру
+
^8.
i,
j
=
l,...,n.
Эта система эквивалентна следующему представлению абсолютных час-
тот rn,j появления биграмм (a^j):
m
ij=^PiPij+^
8e
ij>
(|в
Ц
|<1,
i,j = l
v
..,n).
Тогда вероятность порождения последовательности с'
£
е равна:
Р(«г)-Р|111Рц
(М)
Логарифмируя равенство, получаем:
fog-77r = -togpi
-2)WpiP
M
+^8e
u
)fogp
4
=
Р(с<)
(Ц)
Далее, оцениваем, сверху модуль разности:
hog
1
Р(с'/)
1
<- log +
<
t Pi,
(2.3.8)
bYjog-.
При i
>
£
0
и достаточно малом 5 из неравенства (2.3.8) следует первое
утверждение теоремы:
1
<Т), где П
ж
= -]£PiPij log ру.
P(cJ)
-H
0
2°.
Ко второму классу С" отнесём все последовательности, для которых нера-
венство (2.3.7) не выполнено, по крайней мере, для одной пары (ij).
Для доказательства второго утверждения теоремы следует оценить сверху
сумму
Ip(k,-*p,pJ>«).
(2.3.9)
(i,j)

69
§ 3. МАРКОВСКИЕ ИСТОЧНИКИ
Зафиксируем пару (ij). В силу эргодичности рассматриваемой цепи
Мар-
кова для произвольного е' > 0 при достаточно большом £ будет выпол-
няться закон больших чисел:
'{к
ГП::
Ш:
—
Pi
1
2
(2.3.10)
для абсолютных частот встречаемости символов и биграмм.
Из неравенств (2.3.10) получаем:
—
~Pi
Ш:
<^>1-2Б'.
Учитывая включение случайных событий
П1:
"
Pij
Г
2 Г V
n
"
Pijmi
'
<
2
Ш
Ч~
]Г
П
"
РцЩ
*
<
2
^С^Шу-РцШ,^!^,
получаем оценку:
р||
т|
- ф
§
| < |т
м
-р
цт1
|
<
|*
j >
1
- 2е'.
Случайное событие
j|mi-^p
s
|<^j
эквивалентно событию
||miPij-'PiPu|<|'P«}-
что для последне
iPij -
*Р|Рц|
< |^Pijj С
||т,р
ц
-
*р,р„|
<
|*J
i
для случайных событий
A = ||m
i
p
ij
-^p
i
p
lj
|<|^| и B = ||m
ij
-p
ij
m
i
|<|^J
Очевидно, что для последнего события имеет место включение
г
Поэтому для случайных событий
справедлива оценка:
р
=
||«П|Р
Ц
-
^PiPij|
< |т
у
-р
4
Ш||
< |*J >
1
- 2б'.
Преобразуем введённые случайные события:
В = jniiPij - ^£ < т
ц
< m
iPij
+ .
}•
2
g
A = <jm
i
p
ij
--^p
i
p
ij
<m,p
u
+^l

70
ГЛАВА
11.
Источники
СООБЩЕНИЙ
f
8 5
=
[~
m
.P»j
+ 2
1 >
^Р«РУ
>
"
га
«Ри
=
|-
m
iPij
-
-t
<
-^p
iPiJ
<
-m
iPij
+ -I
Откуда получаем:
A
+
В
=
{-8^ < my -^р^у <
8^}= {jmy
-
^
Pi
py| <
8^}.
p(|my
-
^PiPy
I
< 8^)>
1
-
2e'.
Вероятность дополнительного события оценивается сверху таким
образом:
р{|ту-ф|ру|^8^}^
2е\
Следовательно,
для
суммы (2.3.9) получаем:
iPJImy
-^PiPijl^5^}< 2s'n
2
<е,
(ч)
если 8
Р
выбрать меньшим,
чем —~.
2п
2
Далее,
из
очевидного соотношения получаем:
£р<с2)
* 1Р(К -
^PiPijI
*
8
•
(23.11)
cJeCJ
(ij)
чем
и
завершается доказательство теоремы
2.3.1.
А
Распространим доказательство первой теоремы Шеннона
на
случай мар-
ковских источников порядка
т.
2
В
сделанных предположениях относительно
цепи реализации источника порядка
m
удовлетворяют закону больших чисел.
Для любых 8
> 0,
в >
0 и
достаточно большой длине
I
последовательности
Г1!у-р(М
1>8|<е,
(2.3.12)
где
т
г
-
абсолютная частота встречаемости буквы
a
s
в
последовательности
С^.
m
P(
a
Jl V'
a
]m)
Jm
(2.3.13)
где
mj
bwi
j
m
-
абсолютная частота встречаемости
m-граммы
(а^
v
..,aj
m
),
Jiv-Jm =lv^n,B последовательности
c^.
Вероятность реализации последовательности
Cg
может быть представлена
следующим образом:
2
См. Библиографию [1].
