Духин А.А. Теория информации

Подождите немного. Документ загружается.

§ 3. ВЗАИМНАЯ СОБСТВЕННАЯ УСЛОВНАЯ

ИНФОРМАЦИЯ

ВЕРОЯТНОСТНЫХ

СХЕМ

Так как выражение (1.3.5) представляет взаимную информацию исходов

,Ь

{

и в то же время оно не зависит от исхода b

, то величину log — рас-

сматривают как собственную информацию, содержащуюся в исходе а

{

[Определение 3.3: Величина I(a

)=/og— называется

собственной информацией,

содержащейся в исходе а^А.

(1.3.6)

Собственная информация, содержащаяся в исходе a

является функцией

только вероятностного распределения схемы А. Она изменяется от нуля в слу-

чае реализации достоверного исхода до бесконечности, когда р(а

) = р

->0.

Величину I(a

) интерпретируют как априорную неопределённость события щ

либо как количество информации, необходимое для разрешения этой неопре-

делённости. Между взаимной информацией двух исходов I(a

;bj) и собст-

венной информацией исхода I(aj) имеется принципиальное различие, состоя-

щее в том, что первое понятие может быть распространено на произвольные,

в том числе и непрерывные, вероятностные схемы. Величина 1(а

) определена

только для дискретных схем.

Случайная величина

Л..,1(аД...

Ia(»i)

имеет математическое ожидание, величина которого определяется по фор-

муле:

-"ZPi

^Pi'

Определение 3.4: Величина EI

(ai) называется средней

собственной информацией.

Очевидно, что Е1

(а|) = Н(А) - средняя собственная информация равна

средней неопределённости при реализации исходов вероятностной схемы А.

На объединенной вероятностной схеме АВ рассмотрим условное

распределение {р^

,...,pj

ГЛАВА

I. ЭНТРОПИЯ и ИНФОРМАЦИЯ ВЕРОЯТНОСТНЫХ

СХЕМ

Определение

3.5:

Величина!^; 1Ъ;)= log — называется

I—"

Pji

условной собственной информацией,

содержащейся в исходе a

, при условии

реализации исхода bj.

(1.3.7)

Условная собственная информация l(aj /bj) также является случайной ве-

личиной, заданной на объединённой вероятностной схеме АВ. Математичес-

кое ожидание её равно:

Е1(а,/Ь,) =

Ep(ij)I(a

)

= -Ep(ij)tog

Pji

= Н(А/В>

(ij) «»

Средняя условная собственная информация равна условной энтропии.

Рассмотрим соотношения, связывающие величины I(aj/bj), I(aj), I(bj),

I(aj/bj),

I(bj/aj).

l(a

bj)= log log

Pjl

+ log -=l(a.) - l(a, /bj)=

(1.3.9)

Pi Pi

= log ^

log

Pij

+ log - = l(bj) - l(a,

/b^.

Усредняя равенство по объединённой вероятностной схеме, получим:

1(А;В)=

Н(А)-Н(А/В) = Н(В)-Н(В/А). (1.3.10)

Отсюда следует, что

1(А;В)

Н(А), 1(А;В) <Н(В).

Для исходов (ajbj) объединённой вероятностной схемы введём понятие

собственной информации.

[Определение3.6:

Величина I(a{b|) = log —— называется

~~^

р(Ш

собственной информацией, содержа-

щейся в исходе (ajbj).

1(1.3.11)

Нетрудно увидеть, что EI(ajbj) =

Н(АВ).

Установим связь между взаимной и собственной информацией исходов

объединённой схемы АВ.

l(<a,bj)) = tog ^~=log -i- = l(a,)+l(b

)=l(b

)+l(a

PijPi Pji4)

§ з. ВЗАИМНАЯ СОБСТВЕННАЯ УСЛОВНАЯ ИНФОРМАЦИЯ ВЕРОЯТНОСТНЫХ

СХЕМ

Подставим величину l(bj /а;) либо l(aj/bj), найденную из соотношения

(1-3.9).

l((a,bj)) =

1(^)4-1^)-%;^).

(1.3.12)

Усредняя (1.3.12) по объединённой вероятностной схеме АВ, получим:

ЩАВ) =Н(А) + Н(В)- 1(А;В), (13.13)

1(А;В) = Н(А) + Н(В) - Н(АВ)

Из теоремы 1.2.1 об условной энтропии получаем, что

1(А;В) > 0.

Для наглядности приведём диаграммы Вена для двух зависимых вероят-

ностных схем А,В:

I(A;B)

В этом случае условной энтропии

ЩА/В) отвечает множество

Н(АВ)\Н(В).

Аналогично:

Н(В/А)=Н(АВ)\Н(А).

' 1(А;В) = Н(А)\Н(А/В) = Н(В)\Н(В/А).

н(А/в;

Н(В/А)

Для независимых вероятностных схем:

Н(А)=Н(А/В;

DQ.

Рис. 3.1

Н(В)=Н(В/А)

Н(АВ)=Н(А) + Н(В).

ЩА/В) = Н(А).

Н(В/А) = Н(В).

1(А;В) =

Н(А)

- ЩА/В) = 0

Распространим введённые понятия на случай трёх вероятностных схем

А,

В,

С. Задаваясь объединённой вероятностной схемой ABC, можно получить ве-

роятность исходов {a b

с},

{а

Ь}, {а},

условные вероятности:

p(ab/c)=^,p(c)*0.

Р(с)

р(Ьс/а)= Р^>,р(а)*0.

Р(а)

p(b/ac)=

P^ES),

р(ас)^0.

р(ас)

ГЛАВА

ЭНТРОпия

и ИНФОРМАЦИЯ ВЕРОЯТНОСТНЫХ

СХЕМ

Определение 3.7: Условной взаимной информацией

l((b;c)/a) между исходами b еВ,с € С,

при фиксированном исходе ае А на-

зывается величина:

l((b;c)/a)= fogfi^^ = I(b/a)-I(b/ac).

p(b/c)

(1.3.14)

(1.3.15)

Используя определение 1.3.1, введём взаимную информацию между парой

(ab) € АВ и исходом се С.

l((ab);c)= log ^^-I(ab)-l((ab)/c).

p(ab)

С учётом соотношений

I(a,b) = I(a) + I(b/a), l((ab)/c)==I(a/c) + I(b/ac) (13.

)

получаем:

l((ab);c)=I(a) + I(b/a)~I(a/c)-I(b/ac) = I(a;c) + l((b;c)/a). (1.3.17)

Можно получить симметричное выражение:

l((ab);c)=I(b;c)+l((a;c)/b). (13.18)

Полученные равенства (1.3.17), (1.3.18) выражают свойство аддитивности

информации.

Определение 3.8: Средней взаимной информацией

между схемами А и В отно-

сительно исхода с € С называется

величина: l((A;B)/c) = El((a;b)/c) =

Ip((ab)/c)l((a;b)/c)

(ab)

= Ip((ab)/c)^^.

(ab) P(

a/c

)

(1.3.19)

§ з. ВЗАИМНАЯ СОБСТВЕННАЯ УСЛОВНАЯ

ИНФОРМАЦИЯ

ВЕРОЯТНОСТНЫХ

СХЕМ

Усредняя эту случайную величину по вероятностной схеме С, получим:

Определение3.9: Средней взаимной информацией

между схемами А и В отно-

сительно вероятностной схемы С

называется величина:

l((A;B)/c)

El((A;B)/c)

= Ep(abc)/^^.

(abc)

р(а/с)

(1.3.20)

Для рассматриваемой вероятностной схемы ABC определено количество

взаимной информации l((ab);c) между исходом (ab) и исходом с. Усредним

эту информацию по схеме ABC

l(AB;C)=EI

ABC

((ab);c)= £p(*bc)fog^^.

(ABC) P(ab)

Из свойства аддитивности информации (1.3.18) получим:

l(AB;C) = I(A;C) + l((B;C)/A)=I(B;C) + l((A;C)/B).

Учитывая (1.3.10), получаем:

(1.3.21)

l(AB;

С) = Н( АВ) - Н(АВ / С) = Н(С) - Н(С / AB). (1.3.22)

Одно из важнейших свойств средней взаимной информации состоит в том,

что 1(А;В) не увеличивается при преобразованиях вероятностных схем. Для

того чтобы сформулировать и доказать это свойство, введём в рассмотрение

отображение:

ЧкА->С. (1.3.23)

Будем предполагать, что <р - сюръективное (возможно биективное) отоб-

ражение.

Задана конечная вероятностная схема АВ и средняя взаимная информация

1(А;В).

Отображение

определяет схему СВ со следующим распределением:

р(с,Ь)=

]Гр(а,Ь).

(1.3.24)

а:ф(а)=с

Средняя взаимная информация 1(С;В) определена для каждого отображения

принимает значения в зависимости от выбора ср.

Теорема 3.1: Для любого сюръективного отображения

ф:

А -> С имеет

место:

1(А;В)>1(С;В) (1.3.25)

Равенство в (1.3.25) имеет место в случае биективного

отображения

ф.

ГЛАВА

ЭНТРОПИЯ

ИНФОРМАЦИЯ ВЕРОЯТНОСТНЫХ

СХЕМ

Доказательство. Рассмотрим схему ABC.

Так как при

выбранном исходе

исход

с € С

однозначно определён

и не

зависит

от

исхода

b е

В,

то

рас-

пределение вероятностей

на

исходах (abc) удовлетворяет условию:

p(c/ab)

p(c/a).

(1.3.26)

С учётом

(1.3.26)

получаем:

p(abc) = p(ab)p(c/ ab)

p(ab)p(c/a),

так

как

p(c/ab)

р(с/а)

1, если

с =

ср(а),

p(c/ab)

p(c/a)

= 0,

если

ф(а).

Из соотношения

(1.3.26)

вытекает:

l((b;c)/a)= bg&£^

tog 1=0. (1.3.27)

р(с/а)

Следовательно, l((B;C)/A)=0.

ПО

свойству

(1.3.21)

аддитивности средней

информации получаем:

I(AC;B) = I(A;B) + l((B;C)/

А)=

1(А;В).

.28)

АС;

В)

1(С;

В)

+1((

А;

В)

/ ф

1(С;

В).

Последнее неравенство имеет место

силу неотрицательности средней

взаимной информации l((A;B)/c).

Сравнивая правые части соотношений

(1.3.28) и (1.3.29),

получаем доказа-

тельство первого утверждения теоремы.

Выражение

(1.3.25)

обратится

равенство, если l((A;B)/c).

Математическое ожидание случайной величины, принимающей неотрица-

тельные значения, равно нулю тогда, когда

все

значения этой случайной

величины нулевые.

нашем случае, когда

яДя

всех исходов

(abc) е

АБС:

р(а/Ьс)

р(а/с).

Последнее условие означает,

что при

выбранном исходе

с € С

исход

а е А

статистически

не

зависит

от b е В. Это

условие всегда выполняется, если

ис-

ход с однозначно определяет исход

а, то

есть если исходы

а и с

однозначно

оп-

ределяют друг друга. Следовательно, отображение

<р

биективно.

Формально, понятие взаимной информации может быть распространено

на

любое конечное число исходов конечных вероятностных схем. Пусть рассмат-

риваются вероятностные схемы

А^.^А^.

ВЗАИМНАЯ СОБСТВЕННАЯ УСЛОВНАЯ ИНФОРМАЦИЯ ВЕРОЯТНОСТНЫХ

СХЕМ

Определение 3.10: Величина: Ца^ ;a

;...;a

) =

(M,s,t)

(к,Лт)

где в числителе дроби помещены произ-

ведения вероятностей всевозможных

т-грамм чётной длины, а в знамена-

теле - нечётной длины, называется

взаимной информацией ис-

ходов

а^а^;...^^

(1.3.30)

Из формулы (1.3.30) следует:

I(a

;...;a,

) =

£l(a

)

-Z*(

i*>

Е^ЛЧ»Ь~

k (Itf) (k£m)

Усредняя это соотношение по объединённой вероятностной схеме, можно

получить формулу, выражающую среднюю взаимную информацию через энт-

ропии частных вероятностных схем.

Основываясь на понятии количества взаимной информации, ниже опреде-

лим пропускную способность канала связи (гл. V, § 1). Будет доказано, что по

каналу можно передавать двоичные сигналы со скоростью, не превышающей

пропускную способность с любой заданной точностью (гл. V, § 3).

Результаты теоремы 1.3.1 используются в доказательстве обратной теоремы

кодирования для двоичного симметричного канала (гл. V, § 3).

§4

Здесь рассмотрено важное свойство выпуклости средней взаимной информа-

ции, на котором будут построены доказательства ряда теорем о свойствах

канала связи (см. гл. V).

Рассмотрим s конечных вероятностных схем Aj,...,A

с одинаковым

множеством исходов:

..,a

и вероятностными распределениями:

Pi(A)

)v-.,Pi(a

)),...,Ps(A)

(p,(ai),.-.»Ps(&m))-

Пусть

..,a

- неотрицательные числа, удовлетворяющие соотношению:

=1.

Введём в рассмотрение вектор:

Ро(А) = £а

(А), 0-4.1)

1=1

также задающий некоторое вероятностное распределение на исходах схемы А.

Пусть матрица

P=|p

|(mxn) (1.4.2)

удовлетворяет условию:

>0,

5^p

Для каждого из распределений

v=l

(A), k =

0,...,s,

найдём распределение

(B),

заданное на исходах схемы

= (b|

,...,Ь

используя для этого матрицу Р.

(B)-p

(A)P, k =

0,...,s.

(1.4.3)

В координатной записи это соотношение принимает вид

Pk(b

)

XPk(

u)Puv>

k=0,s,v=l,n

(143»)

Согласно

(1.3.10)

средняя взаимная информация для любой пары распреде-

лений

(А),р

(В),

k =

..,s,

равна

(А;В)

(В)-Н

(В/А), (1.4.4)

где

(В)

= -]Tp

)/0g

v=l

(B/A) = -

)p(b

gp(b

k = 0,l,...,s.

u=lv=l

ВЫПУКЛОСТЬ СРЕДНЕЙ ВЗАИМНОЙ ИНФОРМАЦИИ

ВЕРОЯТНОСТНЫХ СХЕМ

§ 4. ВЫПУКЛОСТЬ СРЕДНЕЙ

ВЗАИМНОЙ

ИНФОРМАЦИИ

ВЕРОЯТНОСТНЫХ

СХЕМ

Теорема

4.1.

Для произвольных распределений {р

(А)},к =

..,s

произвольных a

..,cc

, a

>0,

J]ot

=1, выполняется

к=1

неравенство:

]JT

(А; В) <

(А;

В).

Доказательство. Рассмотрим разность:

А1(А;В) = £a

(A;B)-

(А;В)

(1.4.5)

(1 4.6)

k=1

= Z

k [H

(В) - H

(B / А)]-

[н

(В)

- Н

(В / А)1

К=1

Получим представление для условной энтропии

(В/А):

(B/

А)

- ££Р

(а„)P(b

/ К)

log

p(b

/а

) =

u=l v=l

u=l

£p(b

/а

)log p(b

/а„) = £a

(B/ A).

V=l

kPk(

Отсюда получаем после подстановки в (1.4.6):

AI(A;B)=^a

(B)-H

(B).

k=l

Преобразуем величину А1(А;В):

S П

А1(А;В) = - £a

) log p

) +

k=l

k-1 v«

(1.4.7)

(1.4.8)

v=l

kPk(b

)

.k=!

log

)= £a

)log

k-l v=l Pkl

Для оценки сверху log

**°Фу)

используем неравенство In

\<>x~-l

(x>0);

Pk(

AI(A;B)<£a

£p

)

Окончательно получаем:

Ро(Ь

)

Pk(b

)

log e = 0.

£a

(A;B)<I

(A;B). A

k=1

Соотношение (1.4.5) показывает, что средняя взаимная информация как

функция m переменных p

(aj)

..,p

) (вероятности р

(Ь!),...,р

(Ь

) выс-

ГЛАВА I. ЭНТРОПИЯ И

ИНФОРМАЦИЯ

ВЕРОЯТНОСТНЫХ

СХЕМ

тупают в роли линейно зависимых переменных) выпуклая на m-мерном сим-

плексе.

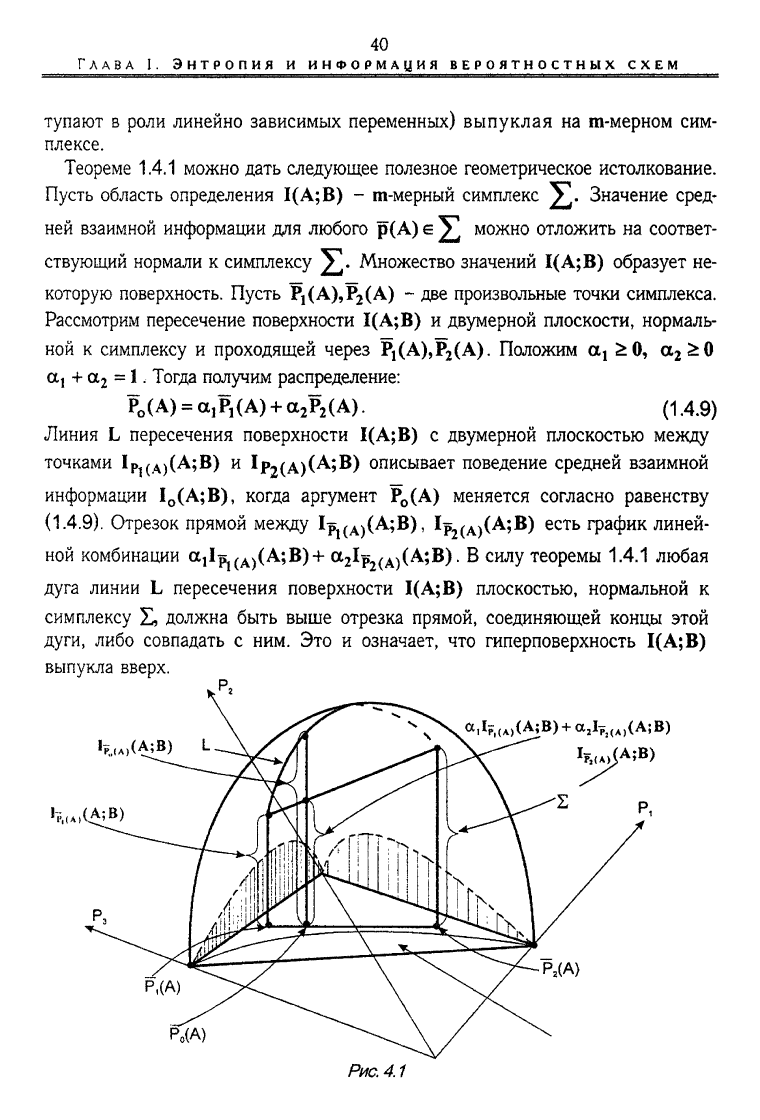
Теореме 1.4.1 можно дать следующее полезное геометрическое истолкование.

Пусть область определения 1(А;В) - m-мерный симплекс Значение сред-

ней взаимной информации для любого р(А) е ]Г можно отложить на соответ-

ствующий нормали к симплексу ]|Г. Множество значений 1(А;В) образует не-

которую поверхность. Пусть Р

(А),Р

(А) - две произвольные точки симплекса.

Рассмотрим пересечение поверхности 1(А;В) и двумерной плоскости, нормаль-

ной к симплексу и проходящей через Pj(A),P

(A). Положим оц £0,

£0

+ а

= 1. Тогда получим распределение:

( А) = а, Р,(А) + а

(А). (1.4.9)

Линия L пересечения поверхности 1(А;В) с двумерной плоскостью между

точками 1р

1(А)

(А;В) и

1р

(А)(А;В)

описывает поведение средней взаимной

информации

(А;В),

когда аргумент Р

(А) меняется согласно равенству

(1.4.9).

Отрезок прямой между Ip

l(A)

(A;B), Ip

2(A)

(A;B) есть график линей-

ной комбинации а^р^д^Аф)* а

1р

2(А)

(А;В). В силу теоремы 1.4.1 любая

дуга линии L пересечения поверхности 1(А;В) плоскостью, нормальной к

симплексу £, должна быть выше отрезка прямой, соединяющей концы этой

дуги, либо совпадать с ним. Это и означает, что гиперповерхность 1(А;В)

выпукла вверх.

Рис.

4.1