Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics

Подождите немного. Документ загружается.

1303

Atoms in Dens

86. Atoms in Dense Plasmas

When plasma densities are high enough that inter-

particle separations are comparable to atomic

dimensions, there are important “environmental”

consequences for atomic structure and atomic

processes. Such conditions are found not only

within stars and giant planets but, nowadays,

also in the laboratory – especially in experiments

related to the quest for inertial conﬁnement

fusion. After introducing important plasma

concepts, we examine these consequences in

regard to several issues: modiﬁcation of atomic

bound states, ionization balance, equation of

state, and radiative and collisional processes

that regulate transport coefﬁcients and the

spectral emission of non-equilibrium plasmas.

Finally, we describe modern simulation methods

that are being used to tackle various many-

body problems in this subject. For nearly

every issue we raise there is a need for better

86.1 The Dense Plasma Environment ............1305

86.1.1 Plasma Parameters....................1305

86.1.2 Quasi-Static Fields in Plasmas..... 1305

86.1.3 Coulomb Logarithms

and Collision Frequencies...........1307

86.2 Atomic Models and Ionization Balance ..1308

86.2.1 Dilute Plasma Models ................ 1308

86.2.2 Dense Plasma “Chemical” Models1309

86.2.3 Dense Plasma “Physical” Models. 1310

86.3 Elementary Processes ...........................1311

86.3.1 Radiative Transitions and Opacity 1311

86.3.2 Collisional Transitions ................1312

86.4 Simulations.........................................1313

86.4.1 Monte Carlo..............................1313

86.4.2 Molecular Dynamics...................1313

86.4.3 The Deuterium EOS Problem........1315

References .................................................. 1316

understanding and for more, and more precise,

data.

Ionized gases, or plasmas, are the predominant form of

matter throughout the universe, and physical conditions

in laboratory and cosmic plasmas vary greatly. No sin-

gle experimental methodology or theoretical construct

sufﬁces to explore all aspects of the plasma state.

Systematic study of plasmas began early in the 20

century, but until recently the physics of atoms in plas-

mas has been largely synonymous with the physics of

isolated ions. This perspective is valid as long as the in-

terparticle spacing is very much larger than the relevant

atomic dimensions, typically a few to a few tens of Bohr

radii. For example, ions are isolated in this sense in inter-

stellar space where the electron density n

≈ 1cm

−3

,or

even in a tokamak, where n

≈ 10

−3

. For neutral

and moderately charged atoms, data such as energy lev-

els, oscillator strengths, and collision cross sections have

long been obtained from traditional kinds of experiments

and quantal calculations, as discussed elsewhere in this

book. Progress in these areas continues to be made, with

the X-ray spectrum of highly-charged Fe [86.1]andthe

Lamb shift in U

+91

[86.2] being noteworthy examples

of the kinds of accurate measurements that can now be

made using electron beam ion traps and storage rings.

The focus of the present chapter is partially ionized

matter in which important atomic phenomena are in-

ﬂuenced by a dense plasma environment. As Fig. 86.1

(which is discussed in detail below) reveals, the densi-

ties in many laboratory and astrophysical plasmas are

high enough to invalidate the presumption of isolated

systems. The interaction of intense laser or particle

beams with solid matter produces rapidly evolving, hot,

and dense plasmas [86.3] that mimic some of the most

extreme conditions in nature, including the thermonu-

clear environment of stellar interiors; these plasmas, as

well as some produced in z-pinch implosions [86.4],

are the basis of world-wide inertial conﬁnement fu-

sion (ICF) efforts. Dense plasmas also can be transient

gain media for ampliﬁed spontaneous emission at X-ray

wavelengths [86.5]. Additional impetus for the study

of atoms in dense plasmas now comes from exper-

iments involving irradiation of solids by ultra-short

(sub-picosecond) laser pulses [86.6]. The moderate tem-

peratures (tens of eV) but high (near-solid) densities

typical of this so-called warm dense matter (WDM)

regime [86.7] produce severely perturbed bound ionic

states.

Part G 86

1304 Part G Applications

210–1–2

18 21 24 27 30

log[T

(K)] log[R

)]

log[Θ

(eV)]

log[n

(cm

–3

)]

= 1 Mbar

NIF main fuel

Sun

Jupiter

White dwarf

Warm dense

matter

= 1

Fig. 86.1 Plasma conditions discussed in the text are identiﬁed on this temperature-density plane. Plasmas below the line

= 1 are strongly coupled, and those below the line Υ = 1 contain degenerate electrons. The HEDP regime, which

lies above and to the right of the line marked P = 1 Mbar, includes some conditions characteristic of warm dense matter.

Also plotted are tracks representing conditions (as a function of radius) within the Sun, Jupiter and a typical white dwarf

star; time-dependent conditions are also shown – from early compression through ignition – within the main (DT) fuel of

a prototype target capsule for the National Ignition Facility

Dense cosmic plasmas – speciﬁcally, the interiors of

stars and giant planets – are very large and have very long

lifetimes. Their thermodynamic variables change only

slowly with position or time and, hence, macroscopic

regions can be considered as statistical systems evolving

through a succession of states in local thermodynamic

equilibrium (LT E). The equation of state (EOS), and the

radiation and heat transport coefﬁcients, viz. the opacity

and thermal conductivity, are key to understanding the

behavior of LTE plasmas. A recent monograph [86.8],

plus comprehensive articles by More et al. [86.9], by

Rogersand Iglesias[86.10], and by Saumonet al. [86.11]

discuss many of the high density consequences for the

opacity and for EOS.

In contrast, the short lifetimes of dense plasmas cre-

ated by intense beam irradiation or by explosive pinch

devices often preclude the establishment of a thermal

distribution of atomic level populations; in extreme

cases, there is not even enough time to establish

a Maxwellian distribution of particle velocities. Pop-

ulations in highly nonequilibrium (non-LTE) laboratory

plasmas, which must be found by solving rate equa-

tions [86.12, 13], are essential information for using

X-ray line emission to diagnose conditions in ICF tar-

gets, or for identifying likely gain media for X-ray

lasing. And, as we discuss in Sect. 86.3, the dense

plasma environment modiﬁes transition rates them-

selves, further complicating the interplay of numerous

collisional and radiative processes in such atomic kinet-

ics calculations.

The topics addressed here are needed for under-

standing non-LTE situations, as well as LTE ones. After

characterizing the perturbing plasma environment in

Sect. 86.1, we summarize well-known prescriptions for

atomic structure and ionization balance in Sect. 86.2,and

then discuss modiﬁed transition rates in Sect. 86.3 for

ions in dense plasmas. Finally, we review in Sect. 86.4

how simulations are now being used to address a wide

array of issues needed to accurately describe atoms in

dense plasmas.

There are several periodic meetings devoted to vari-

ous aspects of this subject, and especially relevant ones

include: Atomic Processes in Plasmas; Radiative Prop-

erties of Hot, Dense Matter; Spectral Line Shapes; and

Strongly Coupled Coulomb Systems. Printed proceed-

ings of these conferences are an excellent guide to recent

developments in the topics discussed here, as well as

numerous other, related ones. Additionally, three re-

cent textbooks [86.14–16] provide detailed treatments

of many of the subjects surveyed here.

The present topic is an important part of what

is now being termed “high energy-density physics”

Part G 86

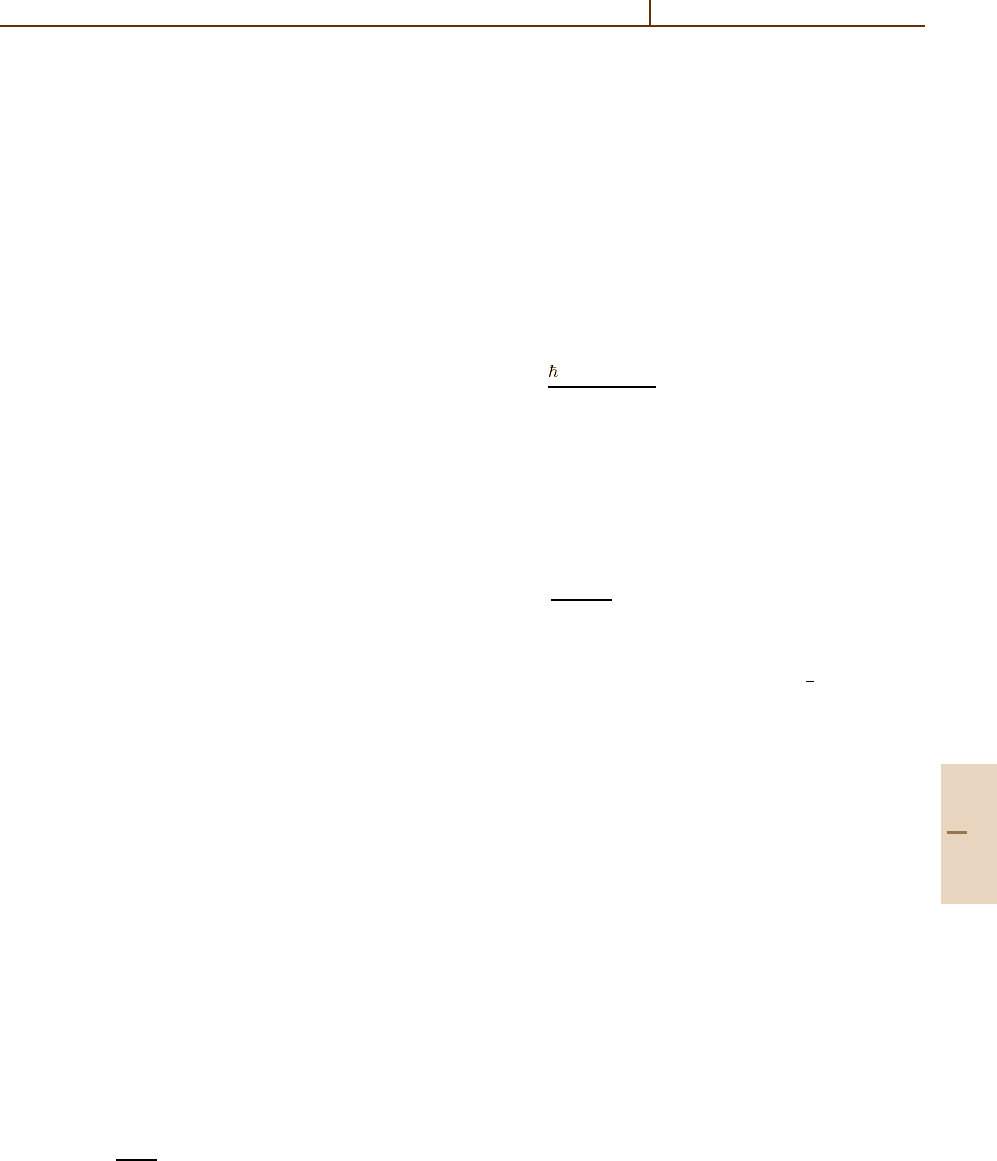
Atoms in Dense Plasmas 86.1 The Dense Plasma Environment 1305

(HEDP). Conventionally this interdisciplinary subject,

which involves collective and/or non-linear phenomena

in many-body systems, is deﬁned as the study of matter

in regimes where the total (matter plus electromagnetic

ﬁeld) pressure exceeds one megabar; this boundary is

also marked in Fig. 86.1. Reference [86.17]isare-

cent National Research Council report on key issues

and opportunities in HEDP.

86.1 The Dense Plasma Environment

Most plasmas are charge neutral, so the mean number

densities n

and n

of constituent ions (charge Z

e,mass

) and electrons (charge −e,massm

) satisfy



= 0 , (86.1)

where the sum ranges over all particle species. Moreover,

plasma conditions usually change slowly enough that

each of the species is able to establish a thermal distri-

bution of velocities, ﬁxed by its temperature Θ

= k

(in energy units). Here, we assume these conditions hold.

86.1.1 Plasma Parameters

A few key quantities characterize the plasmas under

consideration. Derivations, and discussions of the roles

of these and other auxiliary quantities can be found in

standard plasma physics texts [86.18, 19], as well as

a recent tutorial article [86.20].

1. The plasma frequency





4πn



1/2







1/2

(86.2)

deﬁnes a timescale



∼ ω

−1



for the particle oscilla-

tions in response to a non-equilibrium charge density

in the plasma.

2. The Debye length





4πn

/Θ



−1/2





−2



−1/2

(86.3)

is the distance beyond which plasma particles effec-

tively screen any localized charge imbalance.

3. The ion-sphere (or electron-sphere) radius



4πn



1/3

(86.4)

deﬁnes a spherical volume associated with a single

particle and is a measure of interparticle spacing

(among particles of species “a”).

4. The Fermi energy



3π



2/3

(86.5)

characterizes the highest occupied energy level in

a zero temperature system of electrons. A dimen-

sionless measure of degeneracy is Υ = Θ

/Θ

Velocity distributions are either Maxwellian or

Fermi–Dirac in the limits Υ  1orΥ  1,

respectively.

5. The Coulomb coupling parameters

(86.6)

give the average ratio of potential to kinetic en-

ergies between species a and b. The reduced

ion-sphere radius and temperature are R

) and Θ

=(m

)/(m

), respec-

tively. When Γ

is greater (less) than 1, that species

is said to be strongly (weakly) coupled. And, when

the number of particles a in a sphere of radius D

(a Debye sphere),



4πn



= 1/(3Γ

)

3/2

,is

small, discreteness of the charge density can be

important in describing certain plasma phenomena.

Figure 86.1 shows that dense plasmas can be strongly

or weakly coupled; further, some of these plasma condi-

tions involve degenerate electrons while others do not.

And, in WDM, one encounters the situation where Υ ∼1

and Γ

∼ 1, which is particularly difﬁcult to treat theo-

retically because several effects are competing amongst

each other. In this ﬁgure, we plot the run of (n

, Θ

)

values for the sun, for Jupiter, and for a typical white

dwarf star (0.6 solar mass, pure C/O core, H/He outer

layers). Also plotted is the track of DT fuel conditions

in an imploding ICF capsule designed for the National

Ignition Facility. Note that all of these systems sample

wide portions of parameter space, and therefore an ac-

curate description of each requires some very different

plasma models.

Part G 86.1

1306 Part G Applications

86.1.2 Quasi-Static Fields in Plasmas

A simple, yet useful description of the plasma en-

vironment is given by the one-component plasma

(OCP) model [86.22], in which particles of a single

kind (Z

) move against a smooth background of

matter having on average the opposite charge den-

sity, ρ(r) =−Z

. Most plasma phenomena can be

described within the context of either this or the two-

component model (electrons and their parent ions, with

= n

). In the more realistic, two-component pic-

ture, electron screening of the (slower moving) ions is

established on a timescale ω

−1

ω

−1

, so it makes sense

to speak of screened, quasi-static ionic ﬁelds.

When there are many electrons in each Debye

sphere, the electrostatic potential Φ(r) near a test charge

Ze placed in an otherwise uniform, neutral plasma is

exponentially reduced from the Coulomb expression,

viz.,

(r) =

exp

(

−r/D

)

(86.7)

(A more elaborate version of this formula, for partially

ionized atoms, has recently been proposed [86.23].) This

“Debye screening” obtains only in weakly coupled plas-

mas and applies only to a test charge at rest. The faster

the charge Ze moves, the less effective is the plasma

at screening it, since only plasma particles with higher

velocities can form the shielding cloud [86.18, 24].

In the opposite limit of large Γ -values, quasi-static

screening is better described by the ion-sphere (IS) pic-

ture [86.19], in which each stationary ion of charge

e is surrounded by Z

electrons, uniformly distributed

throughout a sphere of radius R

, to produce the potential

(r) = Z



1/r −(1/2R

)



3 −r



(86.8)

inside the sphere, and zero potential outside.

Consideration of a plasma’s electric microﬁeld illus-

trates these concepts. Moreover, microﬁelds are a key

ingredient in calculations of spectral line broadening in

plasmas – an important subject discussed in Chapts. 59,

19 and in [86.14–16].

Local ﬂuctuations in the density of any species about

its mean value n

create a microscopic electric ﬁeld

(r, t). There is a probability distribution P(

) that

characterizes the strengths of these microﬁelds, which

are quasi-static within time intervals short compared

with the ﬂuctuation timescale, 1/ω

. Holtsmark ﬁrst cal-

culated this distribution at an arbitrary position in an

inﬁnite, isotropic gas of noninteracting particles, and

Chandrasekhar [86.25] gives a thorough account of this

famous stochastic problem. Holtsmark’s formula is

(ε) = (2ε/π)

∞



x sin(εx) exp



−x

3/2



dx ,

(86.9)

where ε =



(8π/25)

1/3



is the scaled ﬁeld, and

=|Z

|e/R

. The mean Holtsmark ﬁeld is ε2.99,

and for ε 1, P

(ε) is well approximated by the distri-

bution of ﬁelds due to a single nearest-neighbor in the

gas,

(ε)  3/



2ε

5/2



(86.10)

Both of these distributions ignore the interactions among

charged particles that become increasingly important

as Γ

grows, because particle positions then tend to

be correlated. Quasi-static ion microﬁelds – at the

position of an ion – therefore become weaker, on av-

erage, as the coupling increases. Figure 86.2 illustrates

this point and shows distributions computed with the

2.0

1.5

1.0

0.5

0.0

0123 4

P( )

Γ = 2.0

Γ = 0.2

Fig. 86.2 The probability distribution P(ε) of scaled mi-

croﬁeld strengths ε for different plasma conditions. The

curve marked H represents the Holtsmark distribution,

which applies to an idealized case of non-interacting par-

ticles (i. e., Γ = 0). The other two curves, with Γ = 0.2

and Γ = 2.0, represent distributions determined by the

APEX model for interacting ions (charge Z = 1) that

are Debye-screened by plasma electrons. In these latter

two cases, the ion density and temperature are, respec-

tively, 1.0×10

−3

and 1.15 eV, and 2.6×10

−3

and 16 eV. After [86.21]

Part G 86.1

Atoms in Dense Plasmas 86.1 The Dense Plasma Environment 1307

APEX method [86.26, 27], which uses a parameterized,

two-particle distribution function “tuned” to yield the

exact second moment





for the distribution func-

tion of ﬁeld strengths experienced by any one ion in

a plasma whose ions are all Debye-screened by electrons

only.

The potentials and microﬁelds discussed above are

based on classical statistical mechanics, even though

dense plasmas are inherently quantum many-body sys-

tems. Reference [86.28] provides a careful discussion of

the merits and limitations of this approach.

86.1.3 Coulomb Logarithms

and Collision Frequencies

It is well known that the total cross section for

elastic scattering of two charged particles, Z

e and

e, diverges at any collision energy E ,asaconse-

quence of the inﬁnite range of the Coulomb interaction.

Plasma transport coefﬁcients (e.g., electrical con-

ductivity and thermal conductivity), however, which

depend ultimately upon momentum transfer in this

elementary process, are ﬁnite. This comes about be-

cause scattering at small center-of-mass angles φ,

or, correspondingly, at large impact parameters b,is

diminished by plasma screening, as in (86.7)and

(86.8).

Following Spitzer [86.29], we argue that there is

some minimum effective scattering angle φ

min

. And,

since the analysis will be based on classical formulae,

there is some maximum scattering angle φ

max

beyond

which quantum effects are important. Between these

limits the Coulomb interaction is taken to be unscreened

and Rutherford’s differential cross section σ

(φ) is ap-

plicable. By assuming that φ

max

also is small, it follows

that the momentum transfer cross section can be approx-

imated as

(E ) = 2π

max



min

dφ

[

sin φ

(

1 −cos φ

)

(φ)

]

≈ πa



max

min



(86.11)

where a =



/E is a characteristic length. The

familiar result (a/2b) = tan(φ/2) ≈ (φ/2) gives σ

terms of minimum and maximum impact parameters,

min

= a (from φ

max

= 1) and b

max

= λ

Finally, if the actual collision energy in the argument

of the logarithm, (λ

/a), is replaced by its mean value,

E =

Θ, the momentum transfer cross section takes the

simple form

(E ) = π





ln Λ ; (86.12)

for a two-component, electron-ion plasma, the argument

of this Coulomb logarithm is

Λ ≈ 1/2Γ

3/2

≈ (# particles in Debye sphere).

(86.13)

Spitzer’s result for σ

yields the simplest expression for

the frequency ν

of electron-ion collisions in a two-

component plasma, deﬁned [86.18] as the mean value

of the reciprocal of the time between collisions,

√



2Θ



3/2

ln Λ. (86.14)

Equation (86.12) is commonly used to determine trans-

port coefﬁcients in weakly coupled plasmas, where

ln Λ 1. In the dense plasma regime, however, the

Coulomb logarithm can be small or even negative at

high enough density, which yields meaningless results

for the cross section. Physically, a small ln Λ arises

from a small λ

(high density and/or low tempera-

ture), which means that collisions can only occur at

very small separations where the Coulomb potential is

largest. Strong collisions can be included in the above

analysis simply by not making a small-angle approxi-

mation in the evaluation of the cross section; the result

is [86.30]

(E ) =







1 +Λ



(86.15)

In obtaining this result – which no longer yields a neg-

ative cross section – no assumption need be made

about the value of φ

max

. One must still choose, how-

ever, b

max

, which will not generally be given by λ

since Debye screening is invalid in the dense plasma

regime. Strong collisions at small separations also bring

in the effects of quantal scattering. These issues are

best circumvented by obtaining the cross section di-

rectly from a quantal calculation involving the chosen

screened potential [86.30, 31]. (Note that the formulae

in [86.31] actually describe the scattering of one un-

screened charge by another charge that is screened, so

they are most relevant to the scattering of fast electrons

by slow ions.)

Eventually, even this formulation will fail when

plasma kinetic processes affect the collision. For

example, hard collisions can alter the velocity dis-

tribution function and collective modes can modify

Part G 86.1

1308 Part G Applications

the static screened interaction potential. Furthermore,

strong coupling introduces ionic structure that corre-

lates the collisions. Accurate calculations must consider

the collision process in the context of an appro-

priate kinetic equation [86.30, 32–34]. When such

a process is carried out, the result can be inverted

to yield “effective” or “generalized” Coulomb loga-

rithms that typically are process dependent [86.18].

Li and Petrasso [86.32] obtained high-order cor-

rection terms for the Fokker–Planck equation, for

example, and Boercker et al. [86.33] generalized the

collision term in the Lenard–Balescu quantum ki-

netic equation to include strong coupling effects.

Additionally, Berkovsky and Kurilenkov [86.34]ex-

tended the strong coupling description to also include

“strong” collisions (those poorly treated within the Born

approximation).

The physics of collisions is directly measured by

resistivity experiments, which employ some method to

heat a solid and attempt to tamp the high-pressure plasma

that is formed. The resistivity is then measured either by

the reﬂectivity or directly through current and voltage

probes. A review of these methods has recently been

given by Benage [86.35].

86.2 Atomic Models and Ionization Balance

A pervasive issue in the study of both laboratory and

astrophysical plasmas is ionization balance: What is

the distribution of charge states Z

of atomic ions in

a particular plasma? Answers impact subjects as di-

verse as cosmic abundances deduced from astrophysical

spectra, and the temporal behavior of laser-heated foils.

Table 86.1 lists the charge-state dependence of several

plasma quantities [86.36]. Here,





and





denote the

mean and mean square ionic charge, respectively, viz.,







ions



ions

(86.16)

For a dense plasma, experimental determination

of actual charge-state distributions, or even





,has

proven difﬁcult. Traditional spectroscopic methods (as

described in the next section) require large atomic data

bases and sophisticated kinetics models, which typically

are run several times to ﬁnd the best match to measured

line shapes and intensities. Recently, however, an X-ray

scattering method (based on the Compton effect) has

been developed to determine





in rapidly evolving

plasmas [86.37]. Instead of detailed atomic data, this

method requires accurate knowledge of the plasma’s

dynamic structure factor [86.18], which in general must

Table 86.1 Some plasma quantities that depend on its ion-

ization balance

Quantity Z-scaling (ﬁxed nucleon density)

(Ideal) gas pressure ∼(





+1)

Electrical resistivity ∼









Thermal conductivity ∼









Ionic viscosity ∼ 1/





Bremsstrahlung ∼









be obtained from a molecular dynamics simulation (as

discussed in Sect. 86.4).

86.2.1 Dilute Plasma Models

Consider a nondegenerate plasma in thermal equilib-

rium at a temperature Θ (for instance, some region of

a star’s interior). The time independent ionization bal-

ance for each element is given by the Saha–Boltzmann

formula [86.38]

Z+1



Z+1



2π



3/2

exp(−I

/Θ) ,

(86.17)

for the density ratio of successive charge states, where

and I

are, respectively, the partition function and

ionization potential for the Z-times ionized atom.

The solution of (86.17) is shown in Fig. 86.3 (top

panel) for the case of solid density aluminum over

a wide range of temperatures. The partition functions

were determined from atomic states of the ground con-

ﬁguration only. The aluminum plasma is predominantly

neutral at temperatures in the few electron volt range

and ionizes stage by stage until it is nearly fully ion-

ized just above one kilovolt. Of course, real aluminum

is not an insulator at solid density and low temperatures,

as Fig. 86.3 would suggest. Major corrections to (86.17)

are evidently needed to incorporate the physics of WDM

(Γ ∼ 1, Υ ∼ 1), especially corrections for partial elec-

tron degeneracy. We will return to this problem in later

subsections.

When conditions change too rapidly for LTE to be es-

tablished, the plasma may evolve through a succession of

“steady states” in which the relative abundances of dif-

Part G 86.2

Atoms in Dense Plasmas 86.2 Atomic Models and Ionization Balance 1309

ferent ion stages are determined by a balance of certain

ionization and recombination rates. Then, in order to an-

swer the straightforward question of what are the relative

abundances of atomic ionization stages, one needs a vast

data base of atomic energy levels, plus collisional and

radiative rates. A set of rate equations must be solved to

determine the populations n

(α) for each quantum state

α of each ion stage Z. Each equation involves transitions

to and from all other states [86.12, 13].

The balance of photoionizations and dielectronic

plus radiative recombinations in low-density, steady-

state plasmas is termed nebular equilibrium, because

these are the conditions appropriate to astrophys-

ical nebulae – regions of ionized gas surrounding

hot stars [86.39]. The balance of collisional ioniza-

tions and dielectronic plus radiative recombinations

in low-density, steady-state plasmas is termed coronal

equilibrium, because these are the conditions appropri-

1.0

0.8

0.6

0.4

0.2

0.0

Temperature (eV)

1 10 100 1000

Temperature (eV)

Charge state fraction

Ideal Saha

+11

<Z>

Thomas-Fermi

Ideal Saha

Saha + CL

Fig. 86.3 The top panel shows fractional abundances of

different charge states of aluminum in thermal equilibrium

at solid density over a range of temperatures, as computed

with the ideal Saha–Boltzmann equation (86.17). The cor-

responding mean charge





isshowninthelower panel,in

addition to the result from Thomas–Fermi theory, as given

by (86.18). Also shown is a modiﬁed Saha formulation that

includes continuum lowering shifts

ate to the solar corona. Most tokamak plasmas also are

in coronal equilibrium. Under coronal conditions, essen-

tially all ions are in their respective ground states and

the ionization balance is a function only of the plasma

temperature [86.40]. As the plasma density increases,

three-body collisions become important, and the result-

ing steady-state ionization balance, which depends on

density as well as temperature, is termed collisional-

radiative equilibrium [86.12]. This situation exists in

most ICF experiments.

Finally, conditions in sub-picosecond laser-plasma

experiments can change so rapidly that none of the

above simpliﬁcations apply. Ionization is strongly time-

dependent, and may involve multiphoton processes.

As we describe below, a dense plasma environ-

ment vastly complicates the determination of ionization

balance. In LTE cases, energy levels are changed and

partition functions are truncated by the phenomenon of

continuum lowering. In non-LTE cases these effects still

occur, but, in addition, radiative and collisional rates

themselves are altered.

86.2.2 Dense Plasma “Chemical” Models

There are two distinct strategies taken to extend the re-

sults of the previous section. One strategy, known as

the “chemical picture”, formulates the Saha–Boltzmann

equation in terms of a free energy F(T, V, {n

}),where

the species populations {n

} are to be determined, and

various corrections due to couplings and degeneracy

can be added to yield a thermodynamically consistent

equation of state that includes atomic physics [86.41].

Because plasma screening attenuates the Coulomb

interaction at long range, atoms and ions no longer have

an inﬁnite number of bound (Rydberg) states, and atomic

partition functions are truncated in a natural way. The

simplest chemical picture is that the onset of continuum

energies has been “lowered” by some amount ∆ I (rel-

ative to the atom’s ground state). When ∆ I is a ﬁxed

quantity, continuum lowering eliminates bound states

whose (unscreened) ionization potentials were less than

∆I, and moves all remaining states closer to the con-

tinuum by this same amount. Thus, levels get shifted

but spectral lines do not. Schemes that use an effec-

tive, single-particle potential to determine a spectrum of

modiﬁed eigenstates produce distinct plasma shifts for

different levels and, hence, spectral line shifts. Experi-

ments show, however, that almost all such predictions

have been inaccurate: actual plasma-induced shifts are

very small and, for most applications, ignorable ([86.14,

Sect. 4.10], [86.15, Sect. 3.5]).

Part G 86.2

1310 Part G Applications

A variety of arguments has been put forth to quantify

continuum lowering, including in particular:

1. determine ∆I from the last distinct spectral line near

a series limit (the Inglis–Teller formula [86.42]);

2. determine ∆I from the atom’s dipolar interaction

with the plasma’s microﬁeld [86.41];

3. determine ∆ I from the binding energy of the ground

state in some speciﬁed, screened Coulomb poten-

tial [86.43, 44];

4. determine ∆I from a rigorous, statistical mechanical

treatment of the atomic partition functions [86.45].

Figure 86.3 (lower panel) illustrates the effect of

continuum lowering on the average ionization state





; here, we solve (86.17) for solid density aluminum

with the ionization potentials shifted by an amount

determined by electron screening in the Debye approx-

imation, ∆I =





. Although we do not plot





for this case when the number of particles in a Debye

sphere is less than ten, it is obvious that a somewhat

higher degree of ionization exists when continuum low-

ering is accounted for.

A recent experiment [86.46] suggests that the Inglis–

Teller prescription for line merging accurately describes

the disappearance of the uppermost members of a spec-

tral series. But simply truncating the number of bound

states and, hence, the internal partition function, does

not yield a self-consistent thermodynamic description

of the plasma [86.41, 47]. In this regard, the true situa-

tion in dense plasmas is far more complicated for two

reasons, and both give rise to a gradual disappearance

of high-lying bound states.

First, excited ionic states can be strongly per-

turbed by one or more nearby ions, which means

that (as the density increases) bound, quasi-molecular

states form and eventually evolve to a conduction

band. Models with names such as “incipient Ryd-

berg states” [86.48], “quasi-localized states” [86.45],

“cluster states” [86.49], “negative-energy continuum

states” [86.50], and “collectivized states” [86.51]have

been developed to capture the complicated physics of

this intermediate regime. Second, space- and time-

dependent density ﬂuctuations give rise to different

perturbing conﬁgurations, which means that the plasma

is more accurately described by the average of an en-

semble of perturbed ionic states than by the individual

states of an ion experiencing the mean (usually spher-

ical) perturbation. In the chemical picture, the most

common approach [86.41, 51, 52] reduces the effec-

tive statistical weight of each (unperturbed) ionic state

by a factor representing the probability that the plas-

ma’s microﬁeld is sufﬁciently strong to Stark ionize

it.

The actual inclusion of dynamical plasma screen-

ing effects on ionic bound states requires a much

more elaborate model [86.53] that, as yet, has not

been incorporated into computer codes simulating high

energy-density plasma experiments. Other computa-

tional studies, involving simple continuum lowering

prescriptions [86.54,55], indicate that an accurate treat-

ment of this phenomenon is essential for understanding

non-LTE,aswellasLTE, situations.

86.2.3 Dense Plasma “Physical” Models

An alternative strategy abandons the distinction be-

tween atomic and plasma electrons; this is known as

the “physical picture” [86.47]. The simplest model

that accomplishes this is that of a nucleus centered in

a charge-neutral, spherical cell of radius R

. An elec-

tronic structure calculation for the total electron density

(r) at temperature Θ, subject to the boundary condi-

tion dn

)/dr =0, is carried out and, once the density

is known, various physical quantities can be obtained.

The advantage of this approach is that effects such as

continuum lowering and degeneracy are naturally and

self-consistently incorporated. Models of this kind are

referred to as either “statistical” models or as “average

atom” (AA) models depending on the manner in which

the electronic structure is determined. The accuracy of

the approach depends on both the sophistication with

which the density is computed and the validity of the

spherical cell boundary condition.

The simplest way to obtain the electronic density

is with a statistical model, such as the ﬁnite-

temperature Thomas–Fermi approximation and its

various extensions to include exchange (“Thomas–

Fermi–Dirac”) and gradient corrections (“Thomas–

Fermi–Dirac–Weizsacker”); these models are covered

in detail in Chapt. 20 for free atoms at Θ = 0. Brieﬂy,

the Thomas–Fermi (TF) model describes atomic charge

densities by treating all electrons as a partially degen-

erate Fermi gas subject to a spherical, self-consistent

electrostatic potential Φ

(r) resulting from the nuclear

charge Z

e and the electrons themselves. Given the sim-

plicity of the TF model, agreement with experiment

(for binding energies) is surprisingly good, usually well

within a factor of two for the thousands of ions in the

periodic table.

Feynman and coworkers [86.56]weretheﬁrstto

use such models to describe hot, compressed atoms and

their thermodynamic properties. Quantities such as the

Part G 86.2

Atoms in Dense Plasmas 86.3 Elementary Processes 1311

internal energy, free energy, and pressure are readily

computable. Extended Thomas–Fermi models are use-

ful for describing properties of matter in dense, cold

stars [86.57], for example. As we have emphasized,

a quantity of particular interest is the average ioniza-

tion state





of the plasma, which can be determined

from the electronic density that extends from cell to cell,

viz.,





4π

). (86.18)

The deﬁnition (86.18) is not unique, however, and some

authors prefer to deﬁne bound electrons as all those in

negative energy states [86.58,59].

It is interesting to note that this intuitive deﬁni-

tion of





,(86.18), is considerably different from that

used in the Saha formulation. This





generally will

have a nonzero value even at Θ = 0, a phenomenon

known as “pressure ionization,” because the ionization

occurs solely due to the ﬁnite value of R

. More [86.59]

published a convenient prescription for ﬁnding ion-

ization potentials and total energies, as predicted by

the TF model, of ions with net charge Z

e between

0.1Z

eand0.9Z

e. In the lower panel of Fig. 86.3 we

show





based on the More/TF result. There is gen-

eral agreement with Saha at high temperatures, where

ionic bound states are much smaller than the interpar-

ticle spacing, but important differences occur at low

temperatures.

Average atom models extend the statistical mod-

els by directly employing the Schrödinger equation

for the electron structure. Typically, a self-consistent

electronic structure calculation is carried out such that

the single-particle levels are thermally populated ac-

cording to a Fermi–Dirac distribution. These models

describe atomic shell structure, which is absent in

the statistical models. Modern versions of AA are

detailed quantum mechanical calculations based on, usu-

ally, ﬁnite-temperature density functional theory (DFT),

with some approximation for the exchange-correlation

potential. A good review of the ﬁnite-temperature

DFT approach has been given by Gupta and Ra-

jagopol [86.60], and [86.61] contains several numerical

comparisons. This approach was pioneered by Rozs-

nyai [86.62, 63], who employed a TF approximation for

the free electrons, and by Liberman [86.64] who con-

structed an AA based on a self-consistent ﬁeld model

with a thermal population of Dirac orbitals for all

states.

There are two major weaknesses of the AA method.

First, the spherical cell neglects asymmetrical ionic con-

ﬁgurations in the plasma and assumes that no ion can

penetrate within the radius R

. And, the AA does not

straightfowardly yield the distribution of ionic stages,

which is important for opacity and transport calcula-

tions. Ying and Kalman [86.65] have introduced a model

that addresses the





issue while also incorporat-

ing strong ionic correlations from neighboring ions.

A DFT-based model that describes both strong coup-

ling and the distribution of ionic stages also has been

published [86.66].

86.3 Elementary Processes

In a truly equilibrium plasma, atomic transitions do not

modify the plasma’s physical state. However, the evolu-

tion of LTE and nonequilibrium plasmas is regulated by

the time rate of change of quantities such as Θ and n

and these in turn depend on transport coefﬁcients such

as the radiative opacity and the thermal conductivity.

The processes controlling these coefﬁcients are in-

duced by various radiative and collisional interactions.

Indeed, so many processes can occur that a major

task is the identiﬁcation of those which are most

important in a particular situation. The plasma envi-

ronment may also alter rates applicable to isolated

atoms, through the perturbation of the atomic states

involved and/or the screening of long-range Coulomb

forces. Further complicating the usual two-body colli-

sion picture is the close proximity of many scattering

centers in a dense plasma. Presently, analysis of any

of these many-body problems requires considerable

simpliﬁcation.

86.3.1 Radiative Transitions and Opacity

For a radiative transition between atomic states α and

β, the absorption and emission rates are proportional to

quantities of the form (∆E)

|α|d|β|

summed over

degenerate substates, where d is the electric dipole op-

erator Chapt. 10,andn =1or3fortheEinsteinB and A

coefﬁcients, respectively. In a dense plasma, changes in

these radiative quantities are due primarily to changes in

the atomic wave functions. Theory predicts that plasma

screening reduces line strengths, and that the reduc-

tion factor increases toward the series limit [86.67, 68].

Part G 86.3

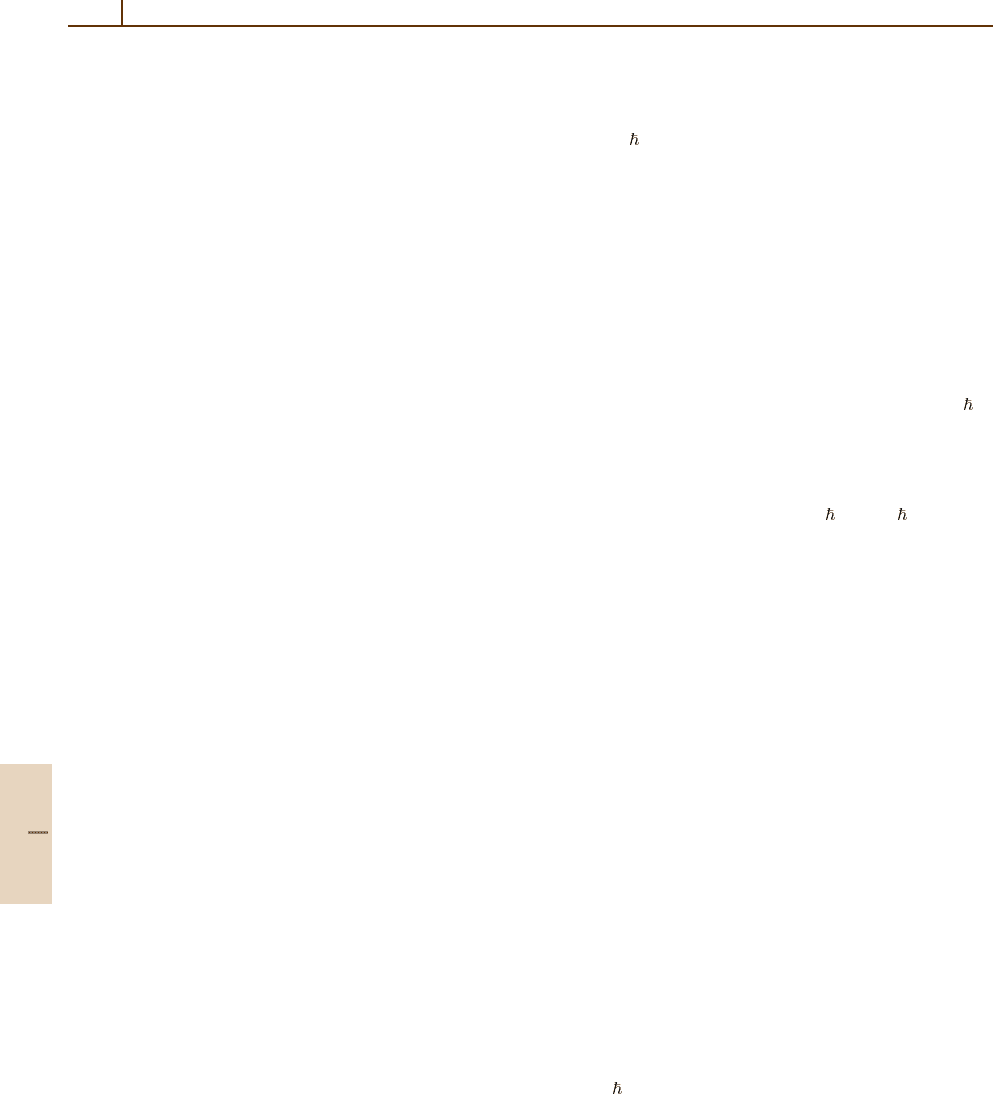
1312 Part G Applications

Also, the cross section for photoejection of an electron

bound by any screened Coulomb potential must vanish

at threshold – in marked contrast to the nonzero pho-

toionization cross sections of isolated atoms and ions.

Since the oscillator strength sum rule still holds, any

diminution of the total bound-bound oscillator strength

must be offset by an increase in the bound-free contribu-

tion; continuum lowering partly accounts for this latter

increase.

Spectroscopic observations of the reduction of decay

rates by plasma screening have been reported [86.69].

But, the plasma densities evidently were too low for this

effect to clearly manifest itself, and alternative expla-

nations have since been given [86.70, 71]. In addition,

there is the more fundamental question of whether static

screening models are even appropriate for the descrip-

tion of radiative processes. As discussed below, this

issue also arises in connection with inelastic collision

processes in dense plasmas.

Several large-scale computer codes are in wide

use to calculate the opacity of hot, dense matter (in

LTE ). Among these, we note the code HOPE [86.62],

which is based on the average atom model; the code

LEDCOP [86.72], which uses accurate (Hartree–Fock)

atomic term data; and the code OPAL [86.73], which

uses detailed conﬁguration accounting and parametric,

(static) screened potentials to compute wave functions

and energy levels. Also, there are some published

results from the new code IDEFIX [86.74], which

is based on a non-spherical (di-center) screened po-

tential arising from the radiating ion and its nearest

neighbor. When making comparisons among these

models, it should be realized that the codes use

quite different line-broadening and continuum lowering

prescriptions.

86.3.2 Collisional Transitions

Various screened Coulomb interactions also can be

used to study plasma effects on inelastic scattering.

References [86.31, 75] and citations therein use either

Debye or ion-sphere potentials, and Born, distorted-

wave, or close coupling approximations, to investigate

excitation processes in plasmas; however, bound states

were left unperturbed. More elaborate static potentials

and perturbed bound states were treated by Davis and

Blaha [86.76, 77], but they did not self-consistently

screen the interaction between projectile and target. For

excitations involving a small transition energy ∆ E, Ki-

tamura [86.78] has recently published a self-consistent

treatment of both (1) the quasi-static perturbations of

the target ion by the microﬁeld, and (2) the dynamically

screened electron-target interaction.

The use of static screening models is invalid when

∆E 

because the collision duration is too short

for any average description of the plasma’s screening

to apply. In such cases, ionization being a particular

example, one must consider the response of the target to

electrodynamic disturbances [86.79]. Reference [86.80]

gives a thorough discussion of this issue, and presents

numerical examples of the effects of projectile and target

screening in ionizing collisions.

Bremsstrahlung is another important plasma colli-

sion process for which static screening models have

been extensively used [86.81–83]. Unfortunately, most

bremsstrahlung radiation emanating from hot plasmas

represents free–free transitions in which ∆E 

(lower frequency emission being attenuated), and in

these situations static screening models are suspect. In

contrast, the formation of laser plasmas occurs mainly

through inverse bremsstrahlung (free–free absorption)

under conditions such that ∆ E =

laser

 ω

,making

static screening models relevant here.

More sophisticated treatments of bremsstrahlung in

dense plasmas [86.84–86] include one or more of the fol-

lowing: strong coupling effects among the plasma ions

(introduced via radial distribution functions [86.22]),

dynamic screening effects involving the electrons (in-

troduced via frequency-dependent dielectric response

functions [86.18]), possible degeneracy effects (in-

troduced via Fermi–Dirac distribution functions for

occupation probabilities of initial and ﬁnal states), and

only partial screening of the nuclear charge by the tar-

get ion’s bound electrons (introduced via a form factor

for the target (Chapt. 56)). Calculations for plasmas with

moderate coupling parameters (Γ ≤ few) reveal that the

ﬁrst three of these effects tend to reduce free-free emis-

sion and absorption rates, while the last effect tends to

enhance the rates. At larger Γ -values, strong ion-ion

coupling tends to drive these rates back up [86.87].

Advances in simulation capability (which we discuss

next) are yielding ever more realistic descriptions of the

dense plasma environment, but what is proving difﬁcult

to improve upon is the ubiquitous use of the Born ap-

proximation to treat all electron-ion scattering events

(see, however, Berkovsky and Kurilenkov [86.34]).

Strong collisions, i. e., those in which the photon en-

ergy

ω is comparable with the relative kinetic energy

of the collision, are particulary important for radiative

losses from plasmas, but these also are just the colli-

sions most likely to be poorly described by the Born

approximation.

Part G 86.3