Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics

Подождите немного. Документ загружается.

Aeronomy 84.1 Basic Structure of Atmospheres 1263

Table 84.4 Composition of the lower atmospheres of

Jupiter and Saturn

Species Mixing Ratio

Jupiter Saturn

0.864

0.94

He 0.136

0.06

0.001 81

0.0045

< 0.002

(0.5–0.2 ppm

)

O 520 ppm

5 ppm

7.0 ppm

0.6 ppm

1.4 ppm

0.02 ppm

0.3 ppm

Ne ≤ 26 ppm

Ar ≤ 9 ppm

Kr ≤ 3.2 ppb

132

Xe ≤ 0.38 ppb

After Strobel [84.25]

After Niemann et al. [84.26]

After Lodders and Fegley [84.27]

probably about 600 K. Because the Voyager data have

not been fully analyzed, the value of T

∞

is uncer-

tain [84.12]. The compositions of the lower atmospheres

of Uranus and Neptune are given in Table 84.5.

Titan, which is a satellite of Saturn, has an N

/CH

atmosphere of intermediate oxidation state. The mix-

ing ratios of components of the lower atmosphere are

giveninTable84.6. The surface P and T are 1.496 bar

and 94 K, respectively. T decreases above the surface

to about 71 K at the tropopause, which occurs at an

altitude of 42 km and a pressure of 128 mbar. A re-

Table 84.5 Composition of the lower atmospheres of

Uranus and Neptune

Species Mixing Ratio

Uranus Neptune

≈ 0.825 ≈ 0.80

He ≈ 0.152 ≈ 0.19

≈ 0.023 ≈ 0.01–0.02

HD ≈ 148 ppm ≈ 192 ppm

D ≈ 8.3 ppm ≈ 12 ppm

≈ 1–20 ppb ≈ 1.5 ppm

≈ 10 ppb ≈ 60 ppb

CO < 40 ppb 2.7 ±1.8 ppm

< 100 ppb < 600 ppb

O 5–12 ppb 1.5–3.5 ppb

After Lodders and Fegley [84.27], except as noted

Courtin et al. [84.28]

Table 84.6 Composition of the lower atmosphere of Titan

Species Mixing Ratio

0.90–0.98

0.01–0.03

2.0×10

−3

CO 60–150 ppm

20 ppm

4 ppm

2 ppm

0.4 ppm

HCN 0.2 ppm

Titan’s atmosphere may also contain up to 14% Ar [84.10]

From [84.29], except as noted

From [84.9]

analysis of the Voyager 1 solar occultation experiment

showed that, above the tropopause, the temperature in-

creases to a peak value of about 176 K at an altitude of

about 300 km. The temperature then decreases to a T

∞

of 153–158 K [84.9]

Triton is a satellite of Neptune. It also has an N

at-

mosphere with small amounts of methane, CO, H

,and

other species. The mixing ratios at 10 km are given in Ta-

ble 84.7. The surface P is about 14–19 µbar. Methane in

the troposphere is in equilibrium with a surface methane

frost at about 38–50 K. The tropopause temperature is

about 36 K, and occurs in the 8 to 12 km region. The

middle atmosphere is isothermal with a temperture of

about 52 K from 25 to 50 km, increasing to 78 K near

150 km [84.30]. T rises to an T

∞

of about 100 K.

Io and Europa are satellites of Jupiter. Both have

transient atmospheres, with mean lifetimes of 2–3 days.

The radius of Io is about 1821 km, and its atmosphere is

Table 84.7 Composition of the atmosphere of Triton

Species Mixing Ratio Comments

0.99 ± 0.01 Below ≈ 200 km

CO 0.0001–0.01 Uncertain

113 ppm

75 ppm

N 3.8×10

−5

ppm

N 290 ppm 100 km (near peak)

H 0.092 ppm

H 1 ppm 30 km (near peak)

3.9×10

−4

ppm

2.9×10

−2

ppm 26 km (near peak)

From [84.15]. Values are at 10 km, except as noted

Part G 84.1

1264 Part G Applications

mostly SO

, which is produced by volcanic plumes. One

model predicts that the average column density of SO

about 10

−3

, and is larger at the equator than at the

poles [84.31]. The atmospheric temperatures range from

100 to 2000 K, and the exospheric temperature is about

1800 K. The altitude of the exobase is about 1400 km.

A plot of the number density and temperature as a func-

tion of altitude is shown in Figure 80–9 k. Europa is

characterized by a radius of 1596 km. The atmosphere

is mostly O

with column density of 5 × 10

−2

and

a scale height of 145 km. The O

is produced by sput-

tering of the ice-covered surface, and is removed in

sputtering by torus thermal ions [84.32]. The ionosphere

is produced by impact of electrons in Jupiter’s magneto-

sphere, and the maximum density of electrons is about

4×10

−3

[84.33].

Mercury does not have a troposphere, mesosphere,

or stratosphere; The pressure at the surface is on the

order of a picobar; thus the surface of the planet is the

exobase. Nevertheless, several atomic species have been

identiﬁed in ﬂuorescence. They are listed in Table 84.8.

Among the possible sources of atmospheric species are

evaporation, ion sputtering, meteoroid bombardment,

and photon-stimulated desorption. Ions produced by

photoionization of neutrals may be picked up by the

solar wind and lost from the atmosphere.

Pluto and its satellite Charon form what is sometimes

referred to as a double planet system. The radius of

Table 84.8 Number densities of species at the surface of

Mercury

Species Number density (cm

−3

)

H 230

hot H 23

He 6×10

O < 4.4×10

(1.7–3.8) × 10

5×10

from Hunten et al. [84.34]

Variable spatially and temporally

Pluto is 1150–1200 km, and that of Charon is about

600 km. The atmosphere of Pluto is mostly N

, with

small amounts of methane, CO, H

, and H. Only upper

limits are available for the mixing ratio of CO. The

surface pressure and temperature are in the ranges 1

to 10 µbar and 35 to 57 K, respectively. Although the

pressure at the surface is approximately the same as

that of the base of the thermosphere on most planets,

the thermal structure of the atmosphere is inﬂuenced

by the large thermal escape ﬂux at the top of the at-

mosphere and by adiabatic cooling. T maximizes near

1200–1260 km radius at about 100 K due to absorption

of solar UV radiation. Above that radius, T decreases

asymptotically to a value of about 80 K [84.35,36].

84.2 Density Distributions of Neutral Species

84.2.1 The Continuity Equation

The density distribution of a minor neutral species j in

an atmosphere is determined by the continuity equation:

∂n

∂t

+∇· Φ

= P

−L

, (84.7)

where Φ

is the ﬂux of species j,andP

and L

are

the chemical production and loss rates, respectively. If

only the vertical direction is considered, the divergence

of the ﬂux becomes ∂Φ

/∂z,andΦ

= n

,where

is the vertical velocity of the species and n

is its

number density. In one-dimensional models, transport

due to turbulence and other macroscopic motions of air

masses is often parametrized like molecular diffusion,

using an eddy diffusion coefﬁcient K in place of the

molecular diffusion coefﬁcient D

. The total transport

velocity w

is then the sum of the diffusion velocity w

and the eddy diffusion velocity w

= w

. (84.8)

If there are no net ﬂows of major constituents, w

and

satisfy the equations

=−D



(1+α

)



(84.9)

=−K



avg



(84.10)

In these expressions, α

is the thermal diffusion fac-

tor (the ratio of the thermal diffusion coefﬁcient to the

molecular diffusion coefﬁcient), and the pressure scale

height H

avg

for a mixed atmosphere is given by (84.5)

with m = m

avg

, the average molecular mass.

Part G 84.2

Aeronomy 84.3 Interaction of Solar Radiation with the Atmosphere 1265

For a stationary atmosphere, if molecular diffusion

greatly exceeds eddy diffusion and if photochemistry

can be neglected, then w

= 0. The resulting number

density distribution is called diffusive equilibrium, and

is given by

(z) = n

)







1+α



exp





−









(84.11)

When mixing processes dominate and w

= 0, the dis-

tribution is given by (84.6), with H = H

avg

84.2.2 Diffusion Coefﬁcients

In the thermosphere of a planet, above the homopause,

the major transport mechanism is diffusion, or trans-

port by random molecular motions. The characteristic

time τ

for molecular diffusion is approximately

. The diffusion coefﬁcient for a species j in

a multicomponent mixture is usually taken as a weighted

mean of binary diffusion coefﬁcients D



k=j

, (84.12)

where f

is the mixing ratio of species k. The binary

diffusion coefﬁcient can be expressed as

16n

Ω

, (84.13)

where µ

is the reduced mass

(84.14)

and n

= n

is the total number density. The colli-

sion integral Ω

is given by

Ω

2π

1/2





5/2

∞



(v)v

exp



−µv

/2k



(84.15)

where v is the relative velocity of the particles, Q

(v)

is the diffusion or momentum transfer cross section

(v) = 2π



(θ, v)(1 −cos θ) sin θ dθ,

(84.16)

and σ

(θ, v) is the differential cross section for elas-

tic scattering of species j and k through angle θ.In

practice, D

is often expressed as b

where n

the total number density and b

is the binary colli-

sion parameter, which is usually given in tabulations

in the semi-empirical form b = AT

.HereA and s

(0.5 ≤s ≤ 1.0) are parameters that are ﬁt to the data.

The binary collision parameter appears, for example, in

the expression for the diffusion limited ﬂux of a light

species to the exobase of a planet (Sect. 84.7).

84.3 Interaction of Solar Radiation with the Atmosphere

84.3.1 Introduction

The source for all atmospheric processes is ultimately

the interaction of solar radiation, either photons or par-

ticles, with atmospheric gases. Since visible photons

arise from the photosphere of the sun, which is character-

ized by T ≈ 6000 K, the solar spectrum in the visible and

IR is similar to that of a black body at 6000 K. At longer

(radio) and shorter (UV and X-ray) wavelengths, the

photons arise from parts of the chromosphere and corona

where the temperatures are higher (10

to 10

K). Thus

the photon ﬂuxes differ substantially from those which

would be predicted for a 6000 K black body. Photons

in the extreme and far UV regions of the spectrum are

absorbed in the terrestrial thermosphere and X-rays in

the lower thermosphere and mesosphere. The solar Ly-

man α line at 1216 Å penetrates through a window in

the O

absorption cross sections to about 75 km. Near

UV photons are absorbed by ozone in the stratosphere,

and visible radiation is not appreciably attenuated by the

atmosphere.

The wavelength ranges that are most important for

aeronomy are the UV and X-ray regions. A solar spec-

trum in the UV and soft X-ray regions at low solar

activity is presented in Fig. 84.2a, and the ratio of a high

solar activity photon ﬂuxes to those at low solar ac-

tivity is shown in Fig. 84.2b. The ratio is near unity

at wavelengths longward of 2000 Å, but increases to

factors that range between 2 and 3 over much of the

extreme UV. At wavelengths between about 100 and

Part G 84.3

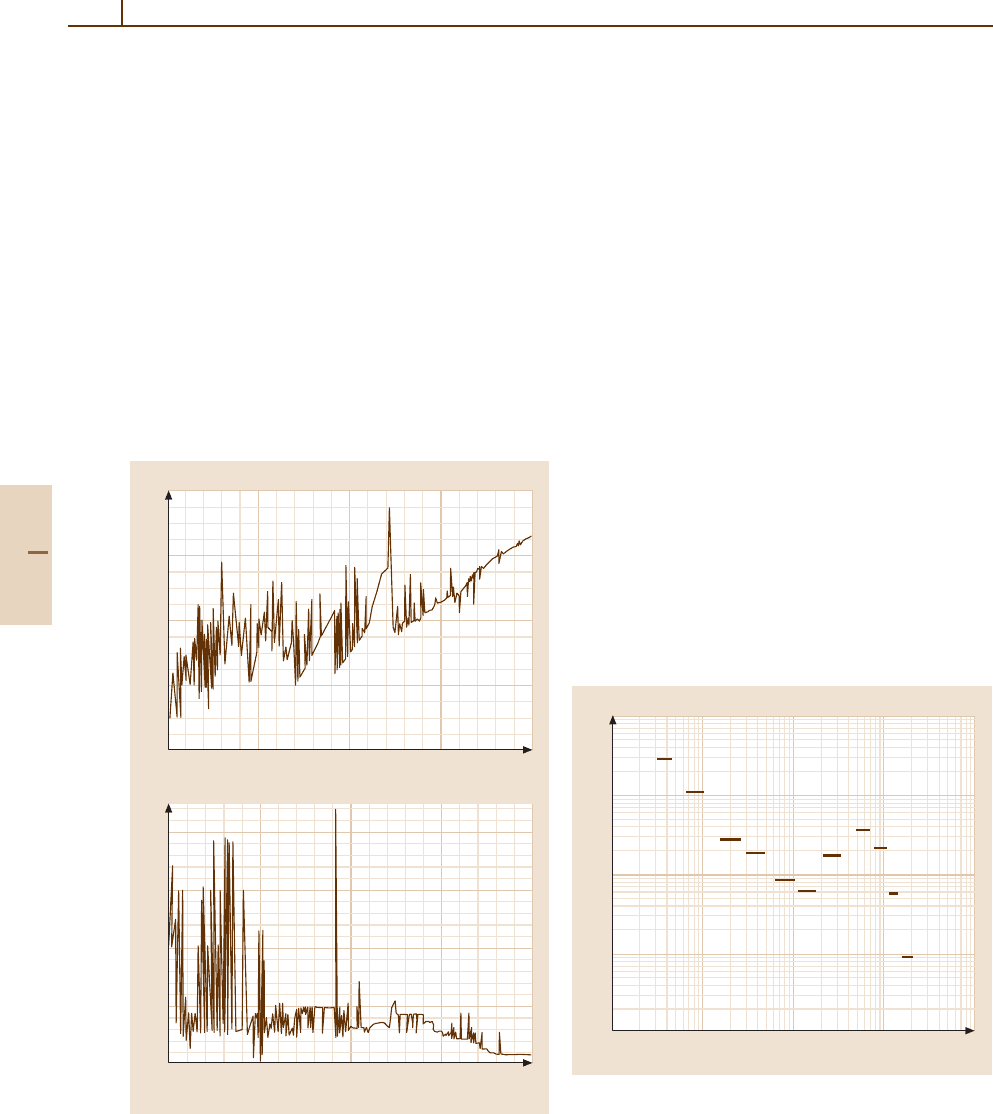
1266 Part G Applications

550 Å, the ratio of high to low solar activity ﬂuxes

reaches values as high as 100. The ﬂuxes at X-ray

wavelengths arise principally from solar ﬂares and can

increase by orders of magnitude from low to high solar

activity.

The sun also emits a stream of charged particles,

the solar wind, which ﬂows radially outward in all

directions, and consists mostly of protons, electrons,

and alpha particles. The average number density of

solar wind protons is about 5 cm

−3

, and the average

speed is about 400–450 km/s at Earth orbit (1 AU). The

interaction of these particles with the magnetic ﬁeld (ei-

ther induced or intrinsic) of a planet, and ultimately

with the atmosphere, is the source of auroral activity.

Terrestrial auroras arise mostly from precipitation of

electrons with energies in the kilovolt range, although

measured spectra vary widely. An example of a pri-

0 500 1000 1500 2000

–2

1.5

0.5

0 500 1000 1500 2000

Wavelength (Å)

log photon flux (10

–2

–1

)

log F

low

Fig. 84.2 (a) Solarspectrumat1AU for 18–2000 Å.

(b) Ratio of the ﬂux at high solar activity to low solar

activity. Plotted with data from Tobiska [84.37]

mary electron auroral spectrum is shown in Fig. 84.3.

Terrestrial auroral emissions maximize in the midnight

sector, but dayside cusp auroras are produced by lower

energy electrons, and diffuse proton auroras are also

observed.

Since charged particles are constrained to move

along magnetic ﬁeld lines, for planets with intrinsic

magnetic ﬁelds, auroras usually occur in an oval near

the magnetic poles, where the dipole ﬁeld lines en-

ter the atmosphere. For Venus, which has no intrinsic

magnetic ﬁeld, auroras are seen as diffuse and vari-

able emissions on the nightside of the planet. On

Earth, low latitude auroras, which arise from heavy

particle precipitation, have also been observed. The

primary particles that are responsible for Jovian au-

rora may be heavy ions originating from its satellite

Io, protons, or electrons. Due to charge transfer, heavy

particles spend part of their lifetime as neutral species,

and their paths may then diverge from magnetic ﬁeld

lines. In any case, a large fraction of the effects of

auroral precipitation is due to secondary electrons, re-

gardless of the identity of the primary particles. In

addition to producing emissions of atmospheric species

in the visible, UV and IR portions of the spectrum,

auroral particles ionize and dissociate atmospheric

species and contribute to heating the neutrals, ions and

electrons.

Flux (eV

–1

–2

–1

) Downward flux

Energy (eV)

Fig. 84.3 Downward electron ﬂux as a function of en-

ergy measured by electron spectrometers on board a rocket

traversing an auroral arc near Poker Flat, Alaska. Af-

ter [84.38] with kind permission from Elsevier Science Ltd.,

Part G 84.3

Aeronomy 84.3 Interaction of Solar Radiation with the Atmosphere 1267

84.3.2 The Interaction of Solar Photons

with Atmospheric Gases

The number ﬂux of solar photons in a small wavelength

interval around λ at an altitude z can, for the most part,

be computed from the Beer–Lambert absorption law

(z) = F

∞

exp[−τ(λ, z)] , (84.17)

where F

∞

is the solar photon ﬂux outside the atmos-

phere, and τ(λ, z) is the optical depth which, in the plane

parallel approximation, is given by

τ(λ, z) =



∞





)σ

(λ) sec χ dz



. (84.18)

Here, σ

(λ) is the absorption cross section of species j

at wavelength λ, and the solar zenith angle χ is the angle

of the sun with respect to the local vertical.

For χ greater than about 75

◦

, the variation of the so-

lar zenith angle along the path of the radiation cannot be

neglected; the optical depth must be computed by nu-

merical integration along this path in spherical geometry.

For χ ≤ 90

◦

the optical depth is

τ(λ, z) =



∞





)σ

(λ)



1−







sin



−0.5



(84.19)

For χ larger than 90

◦

, the optical depth is given by

τ(λ, z) =





∞





)σ

(λ)



1−







sin

◦



−0.5



−

∞





)σ

(λ)



1−







sin



−0.5





(84.20)

where z

is the tangent altitude, the point at which the

solar zenith angle is 90

◦

for the path of solar radiation

through the atmosphere.

In a one-species atmosphere, the rate of absorption

of solar photons of wavelength λ is

(λ) = F

(λ)n . (84.21)

For an isothermal atmosphere in which H(z) ≈ const.,

the absorption maximizes where τ(λ, z) = 1. This is

a fairly good approximation even for regions of the

atmosphere where the H(z) is not constant. The alti-

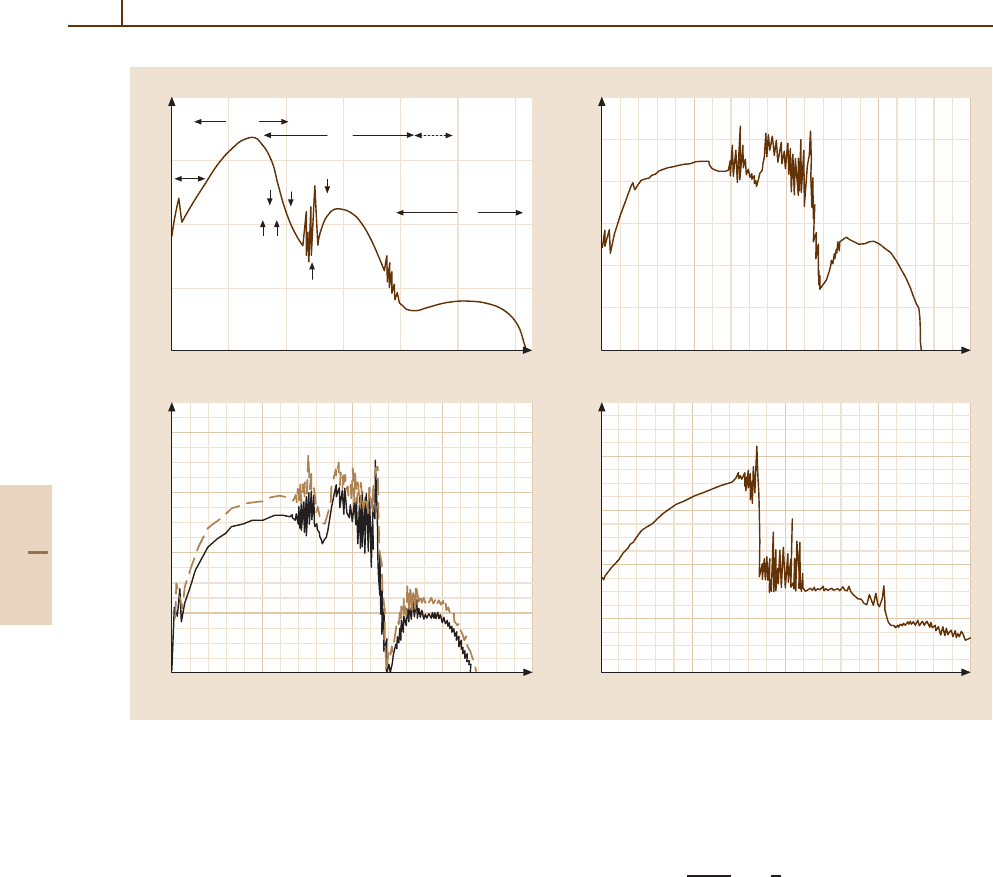
tude of unit optical depth is shown for wavelengths

from X-rays to the near UV for overhead sun in

the terrestrial atmosphere in Fig. 84.4a. Similar plots

for Venus, Mars and Jupiter are shown in Fig. 84.4b,

Fig. 84.4c, and Fig. 84.4d, respectively. N

does not ab-

sorb longward of about 100 nm, so in the terrestrial

atmosphere, O

and O

are the primary absorbers be-

tween 100 and 220 nm, while ozone dominates the

absorption for wavelengths in the range 220–320 nm.

On Venus and Mars, CO

is the main absorber of FUV

and EUV radiation, although at wavelengths less than

about 100 nm, N

, CO, and O also contribute. On Titan,

methane is the primary absorber of UV radiation be-

tween 1400 Å and the absorption threshold of N

, near

1000 Å.

The interaction of UV photons with atmospheric

gases produces ions and photoelectrons through pho-

toionization, which may be represented as

X +hν → X

−

, (84.22)

and photodissociative ionization

AB +hν → A

+ B+ e

−

. (84.23)

In these equations, X represents any atmospheric

species; A is either an atom or a molecular fragment

and AB a molecule. The energy of the photoelectron in

reaction (84.22)isgivenby

= hν − I

− E

(84.24)

and in reaction (84.23)is

= hν − E

− I

− E

, (84.25)

where I

is the ionization potential of species j, E

the dissociation energy of molecule AB,andE

is the

internal excitation energy of the products. Neutral frag-

ments, which may be reactive radicals, are also produced

in photodissociation

AB +hν → A+ B . (84.26)

Part G 84.3

1268 Part G Applications

Lyman α

AIR

0 50 100 150 200 300250

Altitude (km)

Wavelength (nm) Wavelength (Å)

200

150

100

160

150

140

130

120

110

100

160

140

120

100

1000

800

600

400

200

0 500 1000 1500 2000 0 500 1000 1500 2000

0 500 1000 1500 2000

Altitude (km)

Altitude (km) Altitude (km)

Wavelength (Å)Wavelength (Å)

Mars Lo

Fig. 84.4a–d The altitude where τ = 1 versus wavelength (a) Earth [84.39] (b) Venus (c) Mars [84.40] (d) Jupiter (Y. H.

Kim, unpublished)

The rate of ionization of a species j by a photon of

wavelength λ at an altitude z is given by

(λ, z) = F

(z)σ

(λ)n

(z), (84.27)

where σ

(λ) is the photoionization cross section. The

rate for photodissociation is given by a similar expres-

sion, with the photoionization cross section replaced

by the photodissociation cross section. The expression

above must be integrated over the solar spectrum to give

the total rate. In addition, it is often necessary to take

into account ionization and/or dissociation to different

ﬁnal internal states of the products, so the partial cross

sections or yields are needed.

In the atmospheres of magnetic planets, photoelec-

trons may travel upward along the magnetic ﬁeld lines

to the conjugate point, where the ﬁeld line re-enters the

atmosphere. In order to model this effect, the differential

(with respect to angle) cross sections for photoionization

(λ, θ) are necessary. The differential cross section is

sometimes expressed as

(λ, θ) =

(λ)

4π

[1−

β(λ)P

(cos θ)] , (84.28)

where θ is the angle between the incident photon beam

and the ejected electron, P

is a Legendre polynomial,

and β is an asymmetry parameter.

84.3.3 Interaction of Energetic Electrons

with Atmospheric Gases

Suprathermal electrons, which are denoted here e

∗−

,and

include both photoelectrons and auroral primary elec-

trons, can also ionize species through electron-impact

ionization

X +e

∗−

→ X

−



−

(84.29)

Part G 84.3

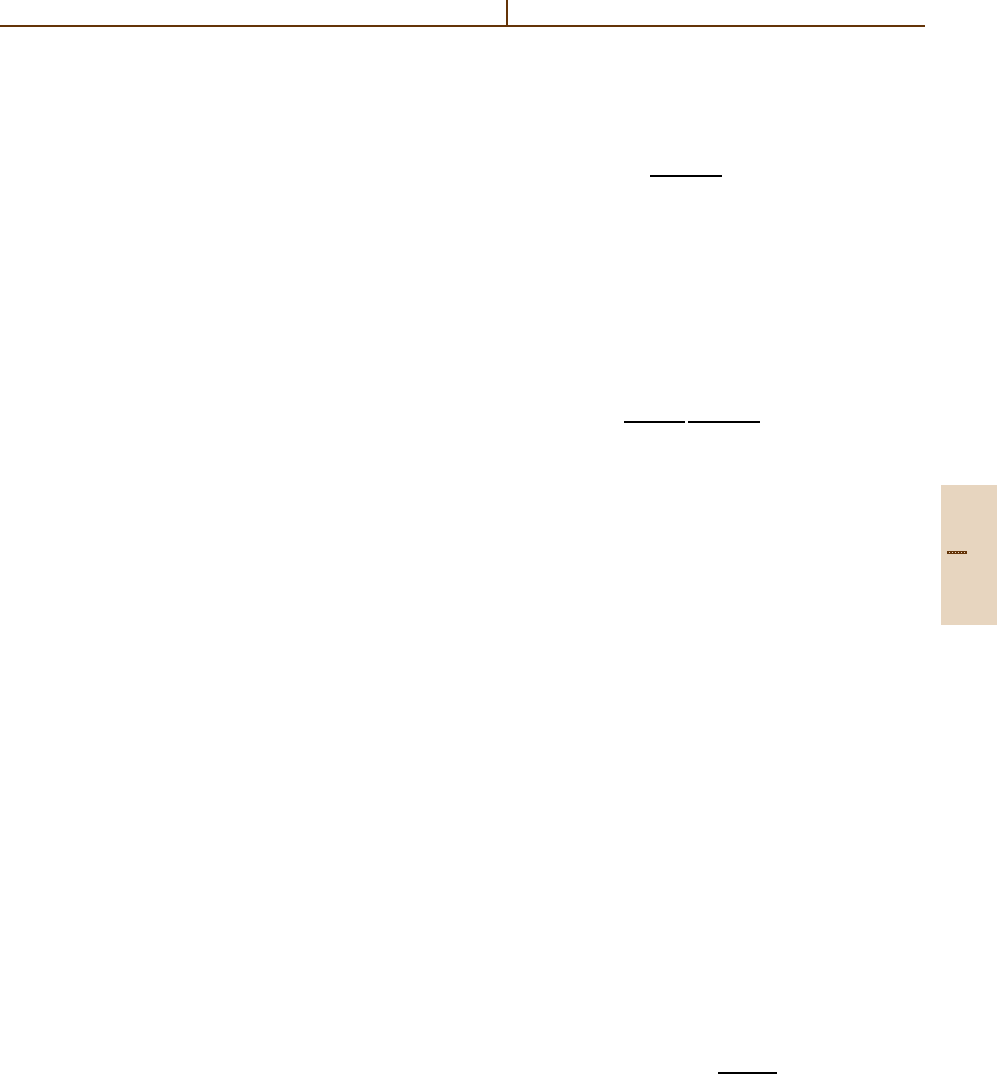
Aeronomy 84.3 Interaction of Solar Radiation with the Atmosphere 1269

and electron-impact dissociative ionization

AB +e

∗−

→ A

+ B+e

−



−

. (84.30)

In these reactions, e

−

represents the energy degraded

photoelectron or primary electron, and e

−

the secondary

electron. The energy of the secondary electron E



in an

electron-impact ionization process (84.29)isgivenby



= E

− I

− E

, (84.31)

where E

is the energy of the primary or photoelectron,

is the energy of the degraded primary or photoelec-

tron, and E

is the internal excitation energy of the

product ions and/or neutral fragments. For the dissocia-

tive ionization process (84.30) the dissociation energy

of the molecule must also be subtracted as well.

Energetic electrons can also dissociate atmospheric

species. In this process

AB +e

∗−

→ A+ B +e

−

(84.32)

the energy of the degraded electron is

= E

− D

− E

, (84.33)

where D

is the dissociation energy of molecule AB.

Collisions with suprathermal electrons can also promote

species to excited electronic, vibrational or rotational

states:

AB +e

∗−

→ AB

†

−

, (84.34)

where the dagger denotes internal excitation. The energy

lost by the electron is thus the excitation energy of the

species.

In determining the rate of ionization, dissociation

and excitation by photoelectrons, the local energy loss

approximation, that is, the assumption that the electrons

lose their energy at the same altitude where they are

produced, is fairly good near the altitude of peak photo-

electron production. The mean free path of an electron

near 150 km is about 30 m. Substantially above the alti-

tude of peak production of photoelectrons, transport of

electrons from below is important, and use of the local

energy loss assumption causes the excitation, ionization,

and dissociation rates to be underestimated. For keV au-

roral electrons, the computation of the energy deposition

of the electrons must consider their transport through the

atmosphere. Thus the elastic total and differential cross

sections for electrons colliding with neutral species must

be employed, as well as the inelastic cross sections, and

the angles through which the electrons scatter must be

taken into account.

In general, the excitation rate q

(z) of a species j

to an excited level k with a threshold energy E

at an

altitude z by electron impact is given by:

(z) = n

(z)

∞



(E)

dF(z, E)

dE ,

(84.35)

where σ

(E) is the excitation cross section at elec-

tron energy E,anddF(z, E)/dE is the differential ﬂux

of electrons (between energies E and E + dE). The ion-

ization rate q

(z) of a species with ionization potential I

due to electron impact is given by

(z)

= n

(z)

∞



(E−I

)/2



dσ

(E)

dF(z, E)

dE ,

(84.36)

where dσ

(E)/ dW

is the differential cross section for

production of a secondary electron with energy W

a primary electron with energy E. The integral over

secondary energies W

terminates at (E−I

)/2 because

the secondary electron is by convention considered to

be the one with the smaller energy. Since the average

energy of photoelectrons is less than 20 eV, the error

incurred in cutting off the integrals in equations (84.35)

and (84.36) at 200 eV or so, rather than (E − I

)/2is

not serious, although for high energy auroral electrons

a larger upper limit may be required.

An estimate of the number of ionizations in a gas pro-

duced by a primary electron with energy E

is E

where W

is the energy loss per ion pair produced,

which approaches a constant value as the energy of

the electron increases. Empirical values are available

for W

for many gases, and usually fall in the range

30–40 eV [84.41].

The total loss function or stopping cross section for

an electron with incident energy E in a gas j is given by

the expression

(E) =



(E)W

(E−I

)/2



)

dσ

(E)

(84.37)

where W

is the energy loss associated with excitation

of species j to excited state k. The differential cross

Part G 84.3

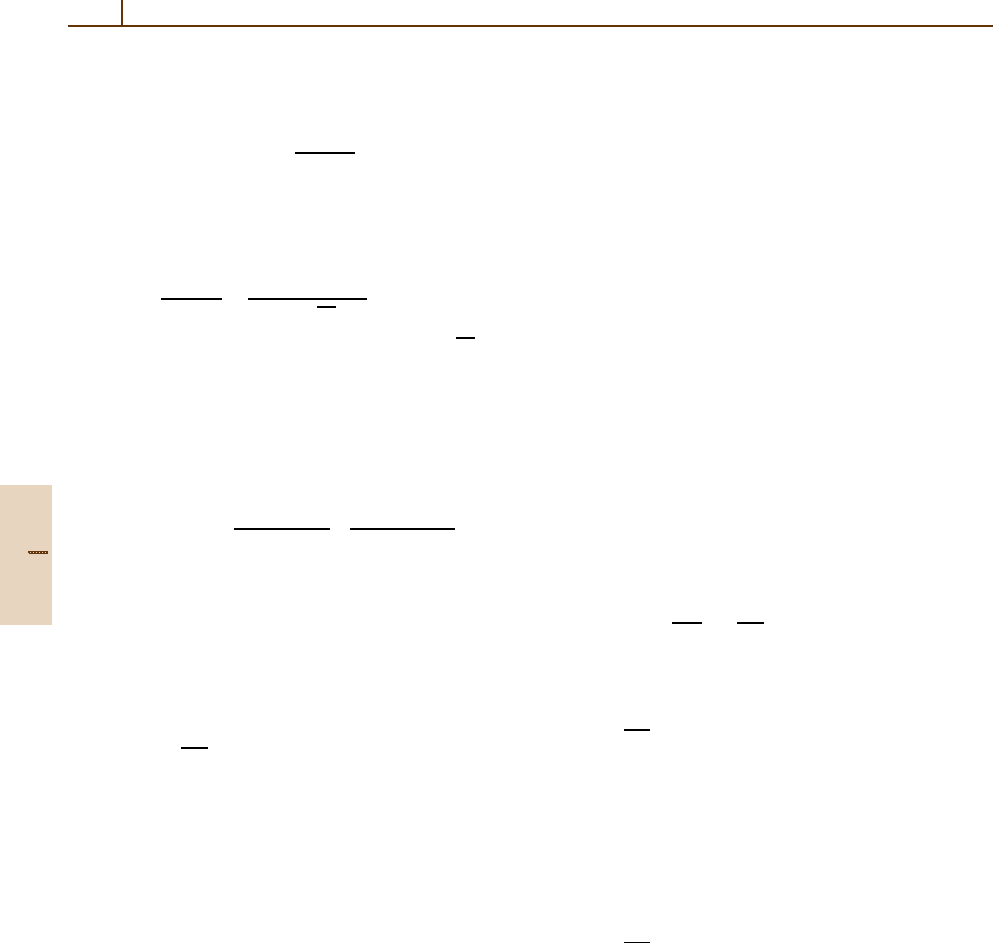
1270 Part G Applications

section is usually adopted from an empirical formula

that is normalized so that

(E) =

(E−I

)/2



dσ

(E)

, (84.38)

where σ

(E) is the total ionization cross section at pri-

mary electron energy E. One formula in common use is

that employed by Opal et al. [84.42]toﬁttotheirdata:

dσ

(E)

A(E)





2.1

, (84.39)

where A(E) is a normalization factor and W is an em-

pirically determined constant, which has been found to

be equal to within a factor of about 50% to the ionization

potential for a number of species.

For energy loss due to elastic scattering by thermal

electrons, an analytic form of the loss function such as

that proposed by Swartz et al. [84.43] may be used:

(E) =

3.37×10

−12

0.94

0.03



E −k

E −0.53k



2.36

(84.40)

where T

is the electron temperature and n

is the number

density of ambient thermal electrons.

For high energy auroral electrons, the rate of energy

loss per electron per unit distance over the path s of the

electrons in the atmosphere can be estimated using the

continuous slowing down approximation (CSDA)as

−



(z)L

(E) sec θ +n

(z)L

(E) sec θ,

(84.41)

where θ is the angle between the path of the primary

electron s and the local vertical. In the CSDA, all the

electrons of a given energy are assumed to lose their

energy continuously and at the same rate. The rate of

energy loss (−dE/ ds) is integrated numerically over

the path of the electron, which degrades in energy un-

til it is thermalized. In this approximation, inelastic

processes are assumed always to scatter the electrons

forward, so cross sections that are differential in angle

are not required. Because electrons actually lose energy

at different rates, however, and because elastic and in-

elastic scattering processes do change the direction of

the electrons, the CSDA gives an estimate for the rates

of electron energy loss processes that is increasingly

inaccurate as the energy of the electron decreases.

In practice, discrete energy loss of electrons can

be easily treated numerically if the local energy loss

approximation is valid. The spectrum of electrons is di-

vided into energy bins that are smaller than the energy

losses for the processes, and the integrals in (84.35, 36)

are replaced by sums over energy bins. Since elastic

scattering of electrons by neutrals changes mostly the

direction of the incident electron, and not its energy,

only inelastic processes need be considered. In order to

compute excitation and dissociation rates, only integral

cross sections are required; the scattering angle is unim-

portant. For ionization, of course, the energy distribution

of the secondary electrons must be considered, but not

the scattering angles of either the primary or secondary

electrons. Below the lowest thresholds for excitations,

energetic electrons lose their energy in elastic collisions

with thermal electrons. The process of energy loss to

thermal electrons is often approximated as continuous,

rather than discrete.

The collision frequency ν

for a discrete electron-

impact excitation process k of a species j is given by

(E) = n

(z)v

(E)σ

(E). (84.42)

For energy loss due to elastic scattering from ther-

mal electrons, a pseudo-collision frequency ν

may be

deﬁned as

(E) =

∆E



−



(84.43)

where ∆E is the grid spacing in the calculation, and the

energy loss rate is

−

= v

(E)n

(E), (84.44)

where L

is taken from (84.40).

Since the energy bins should be smaller than the

typical energy loss in order to obtain accurate rates for

the excitation processes, it is often convenient to treat

rotational excitation also as a continuous process, with

a pseudo-collision frequency similar to that for elastic

scattering from ambient electrons (84.43) with

−

= v

(E)n

rot

(E), (84.45)

where the loss function for rotational excitation is given

rot

(E) =





J,J



(E)W

J,J



. (84.46)

In this expression, η

is the fraction of molecules

jmeasured or computed cross section for electron-

impact excitation of species j from rotational state J

to rotational state J



,andW

J,J



is the associated energy

loss.

Part G 84.3

Aeronomy 84.4 Ionospheres 1271

The slowing down of high energy auroral primary

electrons or photoelectrons arises from both elastic and

inelastic scattering processes, and cannot be treated us-

ing the local energy loss approximation. In solving the

equations for electron transport, theangle through which

the primary electron is scattered, as well as the change in

energy of the primary electron and the production of any

secondaries, must be taken into account. Thus differen-

tial cross sections for the elastic and inelastic scattering

of electrons by neutral species are required. The detailed

equations for electron transport have been presented by,

for example, Rees [84.44].

Several methods for approximating the energy de-

position of auroral electrons are currently in use. The

CSDA has already been discussed, but it provides

only a rough approximation to the depth of penetra-

tion of the electrons, and the rates of excitation, ion

production, and other energy loss processes. In the

two-stream approximation, the electrons are assumed

to be scattered in either the forward or backward di-

rection [84.45]. Implementation of this method requires

only the backscattering probabilities, rather than com-

plete differential cross sections. The method has been

generalized to multi-stream models, in which the solid

angle range of the electrons is divided into 20 or more

intervals, so more or less complete differential cross sec-

tions are required [84.46,47]. Monte Carlo methods have

also been used to model auroral precipitation [84.48].

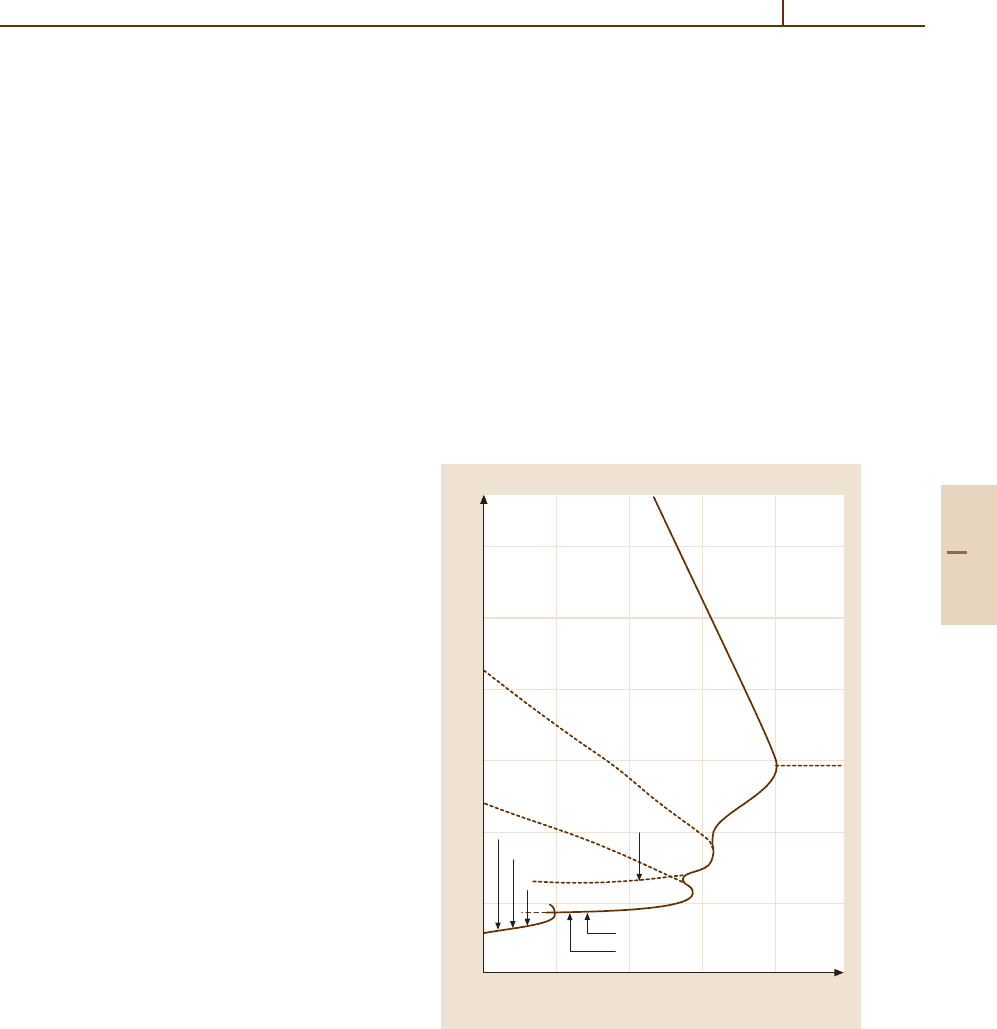
84.4 Ionospheres

84.4.1 Ionospheric Regions

The division of the ionosphere into regions is based

on the structure of the terrestrial ionosphere, which

consists of overlapping layers of ions. These layers

are the result of changes both in the composition of

the thermosphere and in the sources of the ioniza-

tion, and are shown schematically in Fig. 84.5.The

major molecular ion layer is the F

layer, which is

produced by absorption of EUV (100–1000 Å) pho-

tons by the major thermospheric species, and occurs

where the ion production maximizes. The E layer is

below the F

layer and is produced by shorter and

longer wavelength photons that are absorbed deeper

in the atmosphere: soft X-rays and Lyman β,which

can ionize O

and NO (Fig. 84.4a). In the D region,

the densities of negative ions ecome appreciable and

large densities of positive cluster ions appear. These

ions are produced by harder X-rays, with λ

 10 Å, and

Lyman α, which penetrates to about 75 km, where it

ionizes NO. The highest altitude peak in the terres-

trial ionosphere is the F

peak, which occurs near or

slightly below 300 km, where the major ion is O

.The

peak density occurs where the chemical lifetime of the

ion is equal to the characteristic time for transport by

diffusion (∼ H

/D).

84.4.2 Sources of Ionization

As discussed in Sect. 84.3, ionization can be pro-

duced either by solar photons and photoelectrons during

the daytime or by energetic particles and secondary

electrons during auroral events. Photoelectrons have suf-

600

500

400

300

200

100

Electron density (cm

–3

)

Altitude (km)

Topside

ionosphere

Bottomside

ionosphere

–

EUV

UV Lyβ 1026Å

Lyα 1216Å

X-Rays (10–100Å)

X-Rays <10Å

Cosmic rays

Fig. 84.5 Ionospheric regions and primary ionization

sources. After Bauer [84.49]

ﬁcient energy to carry out further ionization if they are

produced by photons with λ

 500 Å. These photons

penetrate further and exhibit larger solar activity vari-

ations than longer-wavelength ionizing photons. Thus

Part G 84.4

1272 Part G Applications

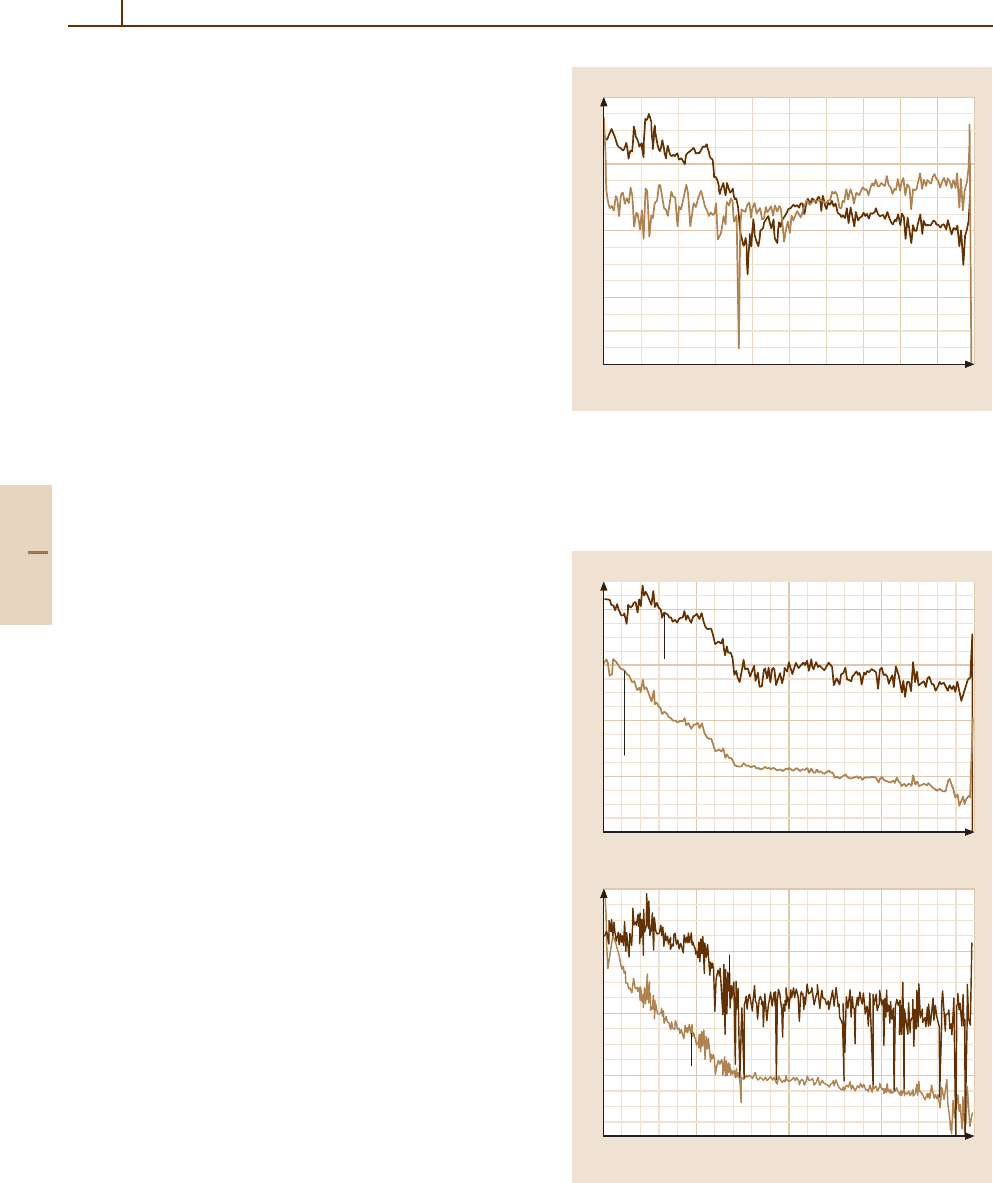
the ionization rate due to photoelectrons peaks below

the main photoionization peak. Primary ﬂux spectra of

photoelectrons produced near the F

peak (172 km) and

below the ion peak (100 km) are shown in Fig. 84.6.The

primary spectrum at the ion peak consists mostly of low

energy electrons, whereas at 100 km, the low energy pri-

maries are depleted, and there are relatively larger ﬂuxes

of electrons with E

 50 eV. Figure 84.7 shows the pri-

mary and steady-state photoelectron spectra near the ion

peaks on Venus and Titan.

The major ions produced in the ionospheres of the

earth and planets are usually those from the major

thermospheric species: N

,andO

on Earth; CO

,andCO

on Venus and Mars; and H

,and

on the outer planets; N

,andCH

in the iono-

sphere of Titan, and N

,andC

in the ionosphere

of Triton. In the presence of sufﬁcient neutral densities,

however, ion–molecule reactions transform ions whose

parent neutrals have high ionization potentials to ions

whose parent neutrals have low ionization potentials.

This is a rigorous rule only for charge transfer reactions,

but it applies more often than not in other ion–molecule

reactions as well.

Because of transformations by ion–molecule reac-

tions, the major ions in the F

regions of the ionospheres

of Earth, Venus and Mars are O

and NO

, in spite of

the large differences in composition between the thermo-

sphere of the earth and the thermospheres of Venus

and Mars. A diagram illustrating the ion chemistry in

the ionospheres of the terrestrial planets is shown in

Fig. 84.8. The vertical positions of the ions in this ﬁgure

represent the relative ionization potentials of the par-

ent neutrals. In regions where there are sufﬁcient neutral

densities the ionization ﬂows downward.

Table 84.9 shows ionization potentials (I

) for sev-

eral major and minor species present in planetary

thermospheres. Major atmospheric species generally

have I

 12–13 eV (λ<900–1000 Å). Only a few

species can be ionized by the strong solar Lyman al-

pha line (1216 Å, 10.2 eV), including NO, and a few

small hydrocarbons and radicals, such as CH

and C

Metal atoms, which are produced in the lower thermo-

spheres and mesospheres of planets from ablation of

meteors, have very low ionization potentials, and some

can be ionized by photons with wavelengths longer than

2000 Å.

Fig. 84.7 Computed primary and steady-state spectra for

photoelectrons near the F

peak on Venus at 1 eV resolution

(top), and Titan at 0.5 eV resolution (bottom). The steady-

state spectra are averaged over three intervals in both plots

160 180 2000 20 40 60 80 100 120 140

Energy (eV)

log electron flux (cm

–2

–1

)

Earth

172km

100 km

Fig. 84.6 Primary photoelectron spectrum for the terres-

trial atmosphere at 172 km (near the F

peak) and at 100 km.

The spectrum at 100 km is signiﬁcantly harder than that at

172 km

Energy (eV)

0 50 100 150 200

Energy (eV)

0 50 100 150 200

log electron flux (cm

–2

–1

)

Venus 140 km

Initial

Steady-state

log electron flux (cm

–2

–1

)

Titan 1000 km

Initial

Steady-state

Part G 84.4