Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics

Подождите немного. Документ загружается.

Quantized Field Effects 78.5 Quasi-Probability Distributions 1149

Expectation values of those s-ordered products are

easily derived from the characteristic function

χ(ξ, ξ

∗

, s) = Tr



ρD(ξ, ξ

∗

, s)



(78.74)

via differentiation



∂

∂ξ





−

∂

∂ξ

∗



χ(ξ, ξ

∗

, s)



ξ=ξ

∗

={(a

†

)

}

 . (78.75)

The Fourier transform of χ yields the quasi-probability

distribution of Cahill and Glauber [78.23]

W(α, s) =



ξχ(ξ, ξ

∗

, s) e

αξ

∗

−α

∗

, (78.76)

where d

ξ = d Re(ξ) dIm(ξ). With this distribution one

is able to calculate the expectation value of any s-ordered

operator product





†









(α

∗

)

W(α, s) d

α. (78.77)

We concentrate now on three important quasi-

probability distributions, namely the cases s = 1, s =0,

and s =−1, corresponding to the Glauber–Sudarshan

distribution, the Wigner function, and the Q function re-

spectively. A detailed discussion of these three functions

can be found in [78.24].

78.5.2 The P Function

The quasi-probability function P(α) was intro-

duced [78.25, 26] as a diagonal representation of the

density operator

ρ =



P(α)|αα| d

α (78.78)

in terms of coherent states |α,(78.26). It is related to

the Cahill–Glauber function W(α, s) via

P(α) = W(α, s =1).

(78.79)

The expectation value of any normally ordered operator

product



†







(α

∗

)

P(α)d

α (78.80)

has a particularly simple form in terms of P(α).

From (78.78)theP function of a coherent state |α



becomes

P(α) =δ

(2)

(α −α

) (78.81)

= δ



Re(α) −Re(α

)





Im(α) −Im(α

)



Quantized ﬁelds for which the P function is positive do

not show nonclassical effects such as squeezing and anti-

bunching. For nonclassical states, such as number states

or squeezed states, the P function only exists in terms of

generalized functions, such as delta functions and their

derivatives, which have a highly singular character.

The positive P-representation P(α, β) for a nondiag-

onal decomposition of a density operator is [78.27,28]

ρ =



α d

|αβ

∗

β

∗

|α

P(α, β) .

(78.82)

The function P(α, β) is a direct generalization of the

Glauber–Sudarshan function P(α),(78.78). P(α, β) ex-

ists for any physical density operator ρ [78.27]andis

given by

P(α, β) =

4π

exp



−

|α −β

∗





(α +β

∗

)



(α +β

∗

)



. (78.83)

Here the state |1/2(α +β

∗

) denotes a coherent state

with the complex amplitude 1/2(α +β

∗

). Note that

P(α, β) is always positive.

78.5.3 The Wigner Function

This quasi-probability was ﬁrst introduced by Wig-

ner [78.29] and may be deﬁned as the distribution

function for a symmetrically ordered operator product

which is obtained in the case s =0. The Wigner func-

tion plays an important role in other branches of physics,

such as quantum chaology, and in particular in any semi-

classical phenomenon when one considers the transition

from quantum mechanics to classical mechanics.

Consider the Wigner function of a quantum mechan-

ical particle of position

x =



2mω



a +a

†



(78.84)

and momentum

p = i



m ω



†

−a



. (78.85)

The Wigner function may be written in terms of position

and momentum variables

W(x, p) =

∞



−∞

dy e

−2i py/

x +y|ρ|x − y ,

(78.86)

where |x ±y denotes position eigenstates. The s =0

Cahill–Glauber deﬁnition and the above deﬁnition of

the Wigner function are related by

W(x, p) =



α =

mωx +i p

√

2m ω

, s = 0



. (78.87)

Part F 78.5

1150 Part F Quantum Optics

The position and momentum distributions of a particle,

or equivalently the quadruture distributions in the case

of a quantized ﬁeld mode, are

Pr (x) =

∞



−∞

W(x, p) d p , (78.88)

Pr ( p) =

∞



−∞

W(x, p) dx . (78.89)

Furthermore, the scalar product

|ψ

|ψ

|

= 2π



dx d pW

|ψ



(x, p)

× W

|ψ



(x, p) (78.90)

of two quantum states is expressed by the phase space

overlap of the two corresponding Wigner functions.

Consequently, any Wigner function W(x, p) has to obey

the necessary condition



dx d pW(x, p)W

|ψ

(x, p) ≥ 0 (78.91)

for all W

|ψ

representing a pure state. For a normalized

state |ψ,



dx d p



|ψ

(x, p)



2π

. (78.92)

Instead of solving the Schrödinger equation for the

dynamics of a massive particle in a potential V(x),we

can try to solve the equation

∂W

∂t

=−

∂W

∂x



r=1,3,..





r−1

∂

∂x

∂

∂p

(78.93)

for its Wigner function W(x, p, t). Note that here only

the odd derivatives of the potential V enter. This equation

is the quantum analogue of the classical Liouville equa-

tion, to which it reduces in the limit of

→ 0. However,

the initial distribution W(x, p, t = 0) has to be a Wigner

function in the sense of (78.86).

Furthermore the Wigner function of an energy eigen-

function in the potential V(x) may be obtained from the

equations



+V(x) −

∂

∂x

−

∂

∂x

∂

∂p



W(x, p)



r=4,6,..





∂

∂x

∂

∂p

= EW(x, p),

(78.94)

and



−

∂

∂x

∂V

∂x

∂

∂p



W(x, p)



r=3,5,..





r−1

∂

∂x

∂

∂p

= 0 . (78.95)

The Wigner function has negative parts for most

quantum states. For example, the Wigner function of

a Fock state |n,

|n

(

p) =

(−1)

−





(78.96)

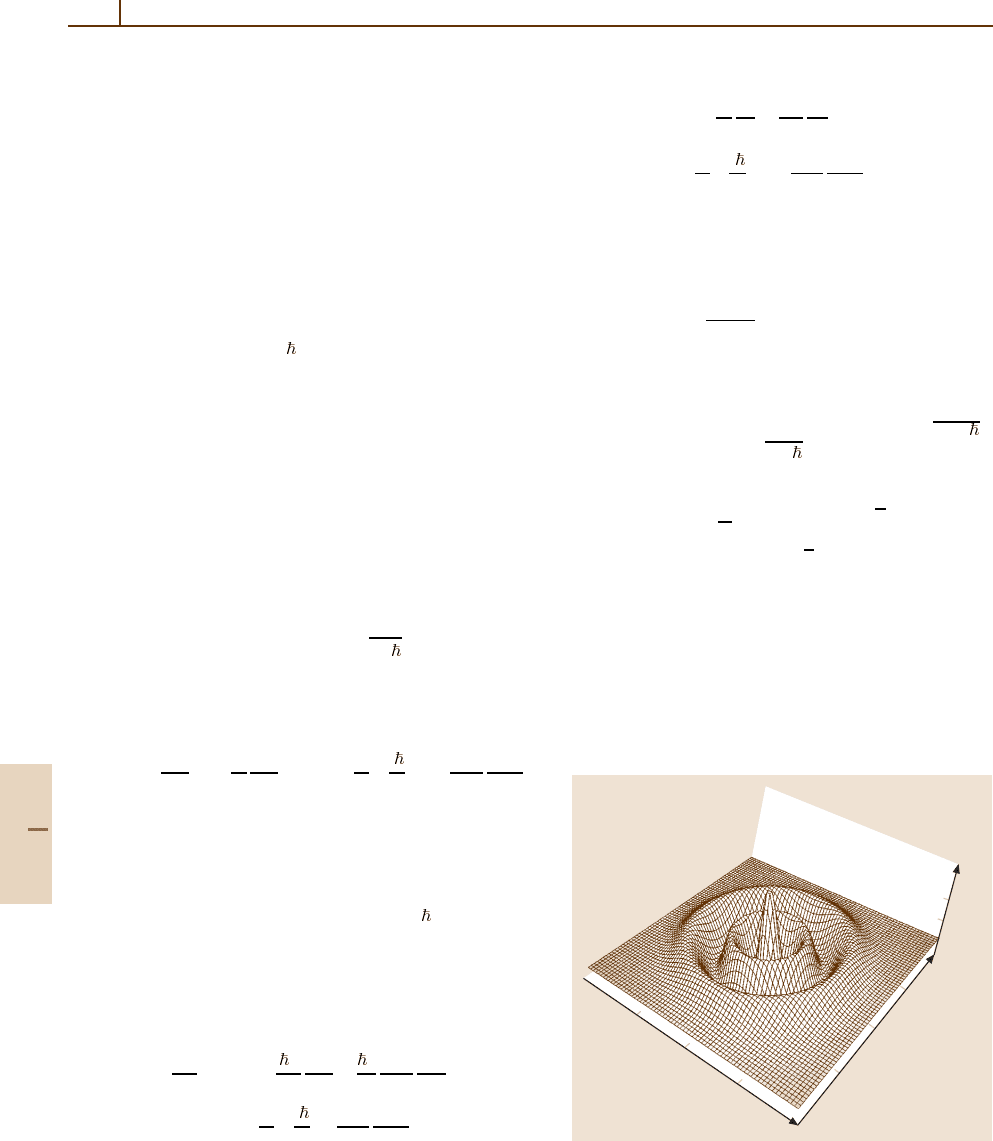
clearly becomes negative due to the oscillating Laguerre

polynomial L

as shown in Fig. 78.4. Note that we have

introduced the dimensionless position

x =

√

mω/ x

and momentum

p = 1/

√

mω p.

On the other hand, the Wigner function

|α,r

(

p) =

exp



− e



x −

√

2Re(α)



− e

−2r



p −

√

2Im(α)





(78.97)

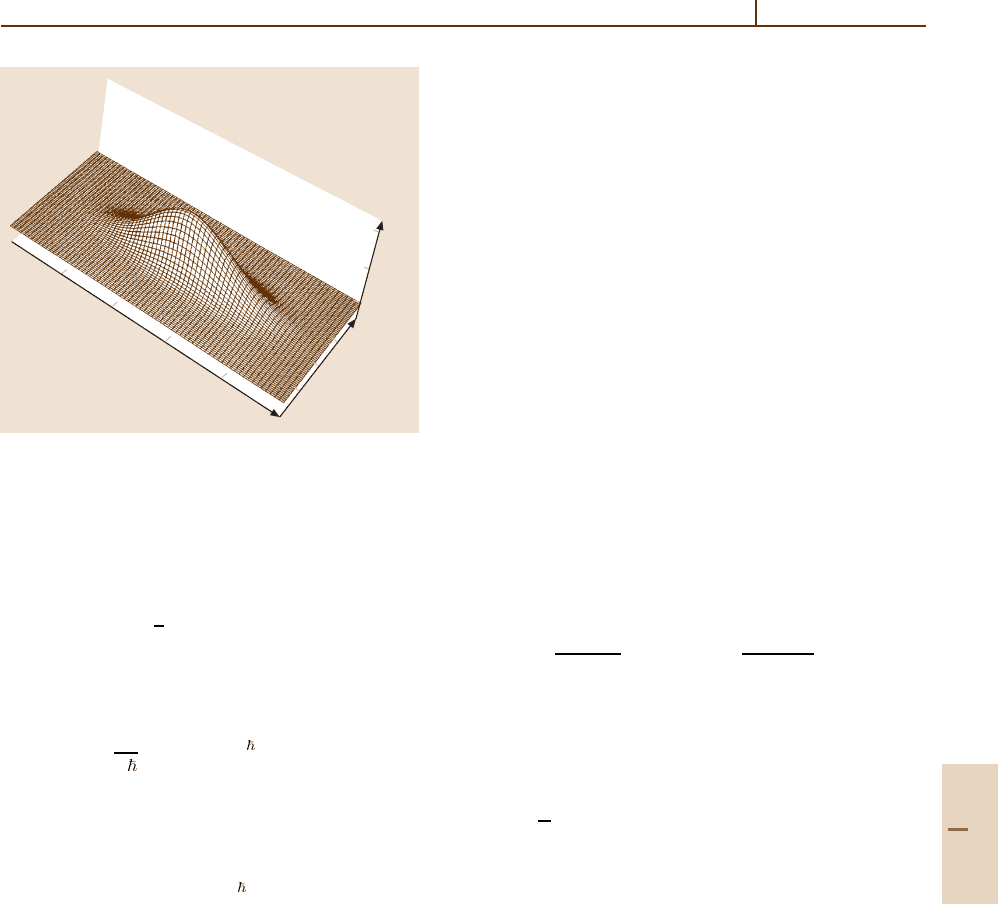
of a squeezed state (78.35) is always positive as shown

in Fig. 78.5. It is a long thin ellipse in phase space

(i. e. a Gaussian cigar). Concerning the negative parts

of the Wigner function, the Hudson theorem [78.30]

states that a necessary and sufﬁcient condition for the

Wigner function of a pure state |ψ to be nonnegative

is that it can be described by a wave function of the

–2

0.2

0.1

W(x, p)

Fig. 78.4 The Wigner function (78.96)ofaFockstate

|n =4. The negative parts can be seen clearly

Part F 78.5

Quantized Field Effects 78.6 Reservoir Theory 1151

–2

0.2

W(x, p)

0.4

–1

Fig. 78.5 The Wigner function of a squeezed state |α, r

with coherent amplitude α = 1 and squeezing e

= 0.25.

For these values the phase space ellipse is oriented along

the x-axis and squeezed in the p-direction. Note that this

function is positive everywhere

form

x|ψ=exp



−

(ax

+bx +c)



. (78.98)

Here a, b and c denote some constants with Re(a)>0.

Finally, the Kirkwood distribution function

K(x, p) =

∞



−∞

dy e

−2i py/

x|ρ|x −2y (78.99)

is a phase space function that resembles the Wigner

function. In the case of a pure state ρ =|ψψ| this

function reduces to

K(x, p) = ψ(x)

ψ(p)e

−ixp/

, (78.100)

where

ψ(p) denotes the Fourier transform of ψ(x).

78.5.4 The Q Function

The Q function is deﬁned by the diagonal matrix elem-

ents

Q(α) =α|ρ|α/π

(78.101)

of the density operator ρ,where|α denotes a coher-

ent state. The Q(α) function is always a positive and

bounded function, which exists for any density oper-

ator ρ.TheQ function is also known as Husimi’s

function. It allows one to calculate expectation values

of antinormally ordered operator products of the form





†







αα

(α

∗

)

Q(α) . (78.102)

Moreover, since the Q function corresponds to the case

s =−1 of the Cahill–Glauber distribution,

Q(α) = W(α, −1).

(78.103)

78.5.5 Relations Between

Quasi-Probabilities

In general, the relation

W(α, s) =

π(s



−s)



β exp



−

2|α −β|



−s



× W(α, s



) (78.104)

holds between two Cahill–Glauber distributions with

the parameters s



> s. In particular, the non-negative

Q function

Q(α) =



β exp[−2|α −β|

]W(β, s =0)

(78.105)

turns out to be a smoothed Wigner function W(β, s = 0).

It is this smoothing process that washes out possible

negative parts in the Wigner function.

78.6 Reservoir Theory

Reservoir theory treats the interaction of one system

with a few degrees of freedom, called the system, with

another system with many degrees of freedom, called

the reservoir. A typical application of reservoir theory

is a microscopic theory of damping: the system inter-

acts with a reservoir, called the heat bath. The system

dissipates energy into the heat bath whereas the heat

bath introduces additional ﬂuctuations to the system.

Since the present chapter focuses on quantized ﬁeld

effects, the reservoir consists of the many modes of

the radiation ﬁeld in free space. Such a reservoir is

modeled by a large number of independent harmonic

Part F 78.6

1152 Part F Quantum Optics

oscillators





†



(78.106)

where b

and b

†

are the annihilation and creation

operators for the ith harmonic oscillator of the reser-

voir. For convenience the interaction with the system

is frequently approximated by a Hamiltonian of the

form

int





†

∗

†



(78.107)

where A is an operator of the small system and

is the coupling strength of this system to the

ith oscillator of the reservoir. For example, A may

be an annihilation operator if the system is a har-

monic oscillator or a Pauli spin matrix in the case of

a two-level atom coupled to the free space radiation

ﬁeld.

Reservoir theory has important applications, and

a detailed discussion can be found in various books,

for example [78.17,20, 27, 28, 31–33].

78.6.1 Thermal Reservoir

The most commonly used reservoir is the thermal reser-

voir or thermal heat bath. Its characteristic properties

are

b

=



†



=b

=



†



= 0 ,

(78.108)



†



. (78.109)

Here

exp

(

)

−1

(78.110)

is the average number of photons at frequency ω

, T is

the temperature of the reservoir, and k

denotes the

Boltzmann constant.

78.6.2 Squeezed Reservoir

Another example of a reservoir is a squeezed vac-

uum or squeezed reservoir. If, for example, multiwave

mixing is used to squeeze the radiation ﬁeld, conju-

gate pairs of the reservoir operators b are correlated.

Therefore, the expectation values b

 and



†



may be nonvanishing. Apart from the average num-

ber

of photons at frequency ω

, which take into

account nonvanishing expectation values



†



, addi-

tional complex squeezing parameters are needed to

describe the reservoir [78.28, 33, 34]. The characteri-

zation of a squeezed reservoir based on noise operators

is discussed in Sect. 78.10.

78.7 Master Equation

In quantum mechanics, density operators are used to

describe mixed states, and are discussed in Chapt. 7.

Here we introduce the concept of the reduced density

operator

= Tr

(

)

(78.111)

which is the density operator ρ

of the complete system

traced over the degrees of freedom of the reservoir. The

equation of motion for ρ

in the Schrödinger picture

(t) =−

{

[

,ρ

(t)

]

}

. (78.112)

In the Born–Markov approximation the trace over the

reservoir can be evaluated and leads to an equation of

motion for ρ

which no longer contains reservoir opera-

tors. This equation of motion is usually called the master

equation. The Born–Markov approximation consists of

two different parts:

1. Born approximation: The coupling to the reservoir

is assumed to be sufﬁciently weak to allow a per-

turbative treatment of the interaction between the

reservoir and the system.

2. Markov approximation: The correlations of the

reservoir are assumed to decay very rapidly on

a typical time scale of the system, or equiva-

lently, the reservoir has a very broad spectrum.

This approximation involves the assumption that

the modes of the reservoir are spaced closely to-

gether, so that the frequency ω

is a smooth function

of i.

Since a general treatment is rather technical, we con-

sider two typical examples. A more general discussion

can be found in [78.17, 20, 27, 28, 31–33]

Part F 78.7

Quantized Field Effects 78.7 Master Equation 1153

78.7.1 Damped Harmonic Oscillator

The universally accepted Hamiltonian in nonrelativistic

QED for a harmonic oscillator of frequency ω coupled

to a reservoir consisting of a large number of harmonic

oscillators is given by the total Hamiltonian [78.35, 36]

= ω



†

a +







†



+ H

, (78.113)

with the linear coupling term





a +a

†



†



(78.114)

and the self-interaction term





a +a

†



. (78.115)

The approach used in quantum optics is to drop the term

and to make the rotating-wave approximation, that

is,todropthetermsab

and a

†

, see also Chapt. 68.

Then the approximate total Hamiltonian reads

= ω



†

a +







†







†



(78.116)

Despite the problems with this approximate Hamiltonian

(see Sect. V.D of [78.35,36] for a discussion) we adopt it

in the present context because it leads to the widely used

master equation for the damped harmonic oscillator. We

consider two reservoirs: a thermal bath and a squeezed

bath.

Harmonic Oscillator in a Thermal Bath

Within the Born–Markov approximation the master

equation is

ρ =

(

n +1

)



2aρa

†

−a

†

aρ −ρa

†





†

ρa −aa

†

ρ −ρaa

†



(78.117)

where

ρ(t) = e

iωa

†

a(t−t

)

(t)e

−iωa

†

a(t−t

)

(78.118)

is the reduced density operator in the interaction picture.

The damping constant γ is given by

γ = 2πD(ω)|g(ω)|

, (78.119)

where g(ω) denotes the coupling strength at fre-

quency ω. The number of thermal photons at frequency ω

n =

exp

(

ω/k

)

−1

(78.120)

Thus the Born–Markov approximation replaces the dis-

crete reservoir modes by a continuum of modes with

a density D(ω).

Harmonic Oscillator in a Squeezed Bath

Within the Born–Markov approximation, the reduced

density operator (78.118) in the interaction picture sat-

isﬁes the master equation

ρ =

(

n +1

)



2aρa

†

−a

†

aρ −ρa

†





†

ρa −aa

†

ρ −ρaa

†



−



†

ρa

†

−a

†

ρ −ρa

†



−

∗

(

2aρa −aaρ −ρaa

)

(78.121)

Here γ is again given by (78.119). The squeezed reser-

voir is characterized by a real number

n and a complex

number

m. Physically n is the number of photons at

frequency ω, i. e., similar to the thermal reservoir, it

measures the average energy at frequency ω.Thecom-

plex number

m determines the amount of squeezing. In

general, the positivity of the density operator requires

≤ n (n +1). (78.122)

A more quantitatively deﬁnition of n and m in terms of

noise operators is given in Sect. 78.10.

78.7.2 Damped Two-Level Atom

The interaction of a two-level atom with a classical

electromagnetic ﬁeld is already discussed in Chapt. 68.

For a quantum mechanical treatment of the ﬁeld we

only have to replace the classical ﬁeld by its quan-

tum mechanical counterpart (78.9). We then ﬁnd in the

rotating-wave approximation (Chapt. 68), that the dy-

namics of a two-level atom with a transition frequency

coupled to a reservoir consisting of a large number of

harmonic oscillators is approximately described by the

total Hamiltonian





†







−

†

∗



(78.123)

Part F 78.7

1154 Part F Quantum Optics

where





,σ

−





(78.124)



0 −1



. (78.125)

Again, two reservoirs are considered: a thermal bath and

a squeezed bath.

Two-Level Atom in a Thermal Bath

Within the Born–Markov approximation, the master

equation is

ρ =

(

n +1

)(

2σ

−

ρσ

−σ

−

ρ −ρσ

−

)

(

2σ

ρσ

−

−σ

−

ρ −ρσ

−

)

(78.126)

where

ρ(t) = e

iω

(t−t

)/2

(t)e

−iω

(t−t

)/2

(78.127)

is the reduced density operator in the interaction picture,

and γ and

n are given by (78.119)and(78.120).

Two-Level Atom in a Squeezed Bath

Within the Born–Markov approximation, the reduced

density operator in the interaction picture, (78.127),

satisﬁes the master equation

ρ =

(

n +1

)(

2σ

−

ρσ

−σ

−

ρ −ρσ

−

)

(

2σ

ρσ

−

−σ

−

ρ −ρσ

−

)

−γ

mσ

ρσ

−γ m

∗

−

ρσ

−

, (78.128)

where γ , n and m have the same meaning as in (78.121).

78.8 Solution of the Master Equation

78.8.1 Damped Harmonic Oscillator

We consider only a thermal reservoir and present the

solution of the master equation (78.117). For

n = 0it

can be solved in terms of coherent states, see (78.26).

For

n = 0 we give solutions in terms of quasi-probability

distributions.

Coherent States

For n =0, which is a good approximation for optical fre-

quencies, if the system is initially in a coherent state |α



with a density operator

ρ(t

) =|α

α

| , (78.129)

then there exists a simple analytical solution of the

master equation (78.117)

ρ(t) =|α

−γ

(

t−t

)

α

−γ

(

t−t

)

| . (78.130)

A coherent state thus remains a coherent state with

an exponentially decaying amplitude α

−γ

(

t−t

)

.Ac-

cordingto(78.78) a general solution

ρ(t) =



P(α

)



−γ

(

t−t

)



−γ

(

t−t

)



(78.131)

can be constructed for an initial density operator

ρ(t

) =



P(α

)|α

α

| . (78.132)

If the system is initially in a superposition

|ψ(t

)=



|α

 (78.133)

of coherent states, the time evolution is given by

ρ(t) =



i,k

∗

exp



−



1 − e

−γ(t−t

)



|α

−α



×exp





1 − e

−γ(t−t

)





∗







−γ

(

t−t

)



−γ

(

t−t

)



(78.134)

For γ(t −t

)  1, the interference terms |α

α

|, i = k

decay with an effective decay constant γ |α

−

/2. Thus the damping constant is modiﬁed by

the separation of the two coherent states in phase

space.

Fokker–Planck Equation

A widely used procedure for solving the master equa-

tion for a damped harmonic oscillator, (78.117), or

for similar problems, is to derive an equation of mo-

tion for the quasi-probability distributions W(α, α

∗

;s)

deﬁned in (78.76) from the master equation. The

operators a and a

†

are replaced by appropriate differ-

ential operators. The substitution rules can be derived

Part F 78.8

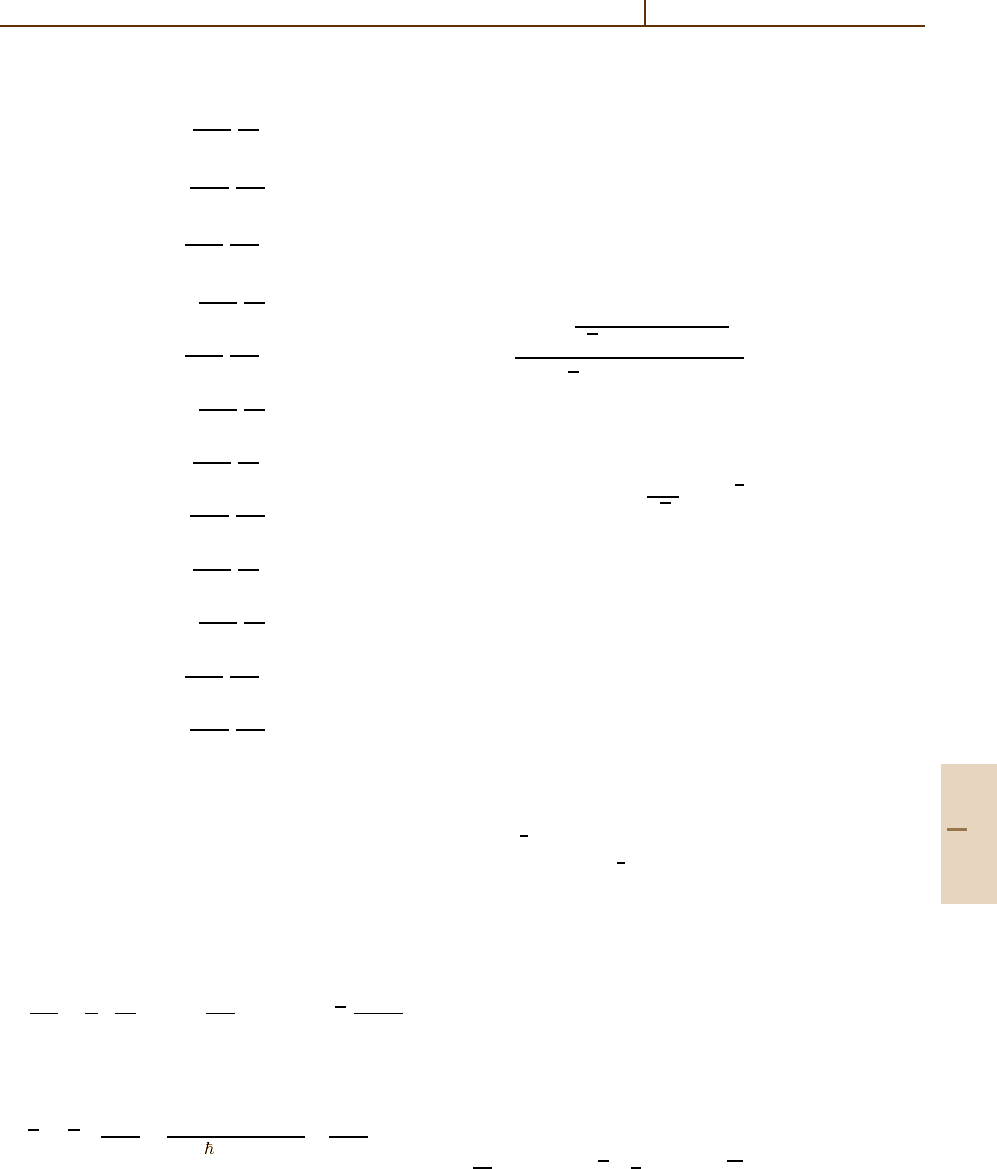
Quantized Field Effects 78.8 Solution of the Master Equation 1155

from (78.73), (78.74)and(78.76)andare



†





ρ →



∗

−

s +1

∂

∂α





α −

s −1

∂

∂α

∗





W ,



†





→



α −

s +1

∂

∂α

∗







∗

−

s −1

∂

∂α



W ,

aρa

†

→



α −

s −1

∂

∂α

∗





∗

−

s −1

∂

∂α



W ,

†

ρa →



∗

−

s +1

∂

∂α





α −

s +1

∂

∂α

∗



W ,

†

ρa

†

→



∗

−

s +1

∂

∂α





∗

−

s −1

∂

∂α



W ,

aρa →



α −

s −1

∂

∂α

∗





α −

s +1

∂

∂α

∗



W .

(78.135)

In general, this procedure leads to equations of motion

which involve higher derivatives of W as exempliﬁed

by the quantum mechanical Liouville equation (78.93)

for the Wigner function. For simple Hamiltonians, how-

ever, this equation has the form of a Fokker–Planck

equation which is well known in classical stochastic

problems [78.27, 37] (Sect. 78.10.2). In particular, for

a damped harmonic oscillator described by the master

equation (78.117), one obtains

∂W

∂t



∂

∂α

(

αW

)

∂

∂α

∗



∗





+γ n

∂

∂α∂α

∗

(78.136)

where

= n +

1 −s

exp

(

ω/k

)

−1

1 −s

(78.137)

The time-dependent solution of this Fokker–Planck

equation has the form

W(α, α

∗

, t;s) =



G(α, α

∗

, t|α



,α

∗

, t



;s)

× W(α



,α

∗

, t



;s) d



, (78.138)

where

G(α, α

∗

, t|α



,α

∗

, t



;s)

exp



−



α −α



−γ(t−t



)/2





1 −e

−γ(t−t



)





πn



1 −e

−γ(t−t



)



(78.139)

is the Green’s function of the Fokker–Planck equation

(78.136). The steady-state solution is

W(α, α

∗

, t →∞;s) =

πn

−|α|

, (78.140)

which is the distribution function of a harmonic os-

cillator in thermal equilibrium with a reservoir of

temperature T .

78.8.2 Damped Two-Level Atom

The density operator

ρ =





(78.141)

for a two-level atom can be written as

ρ =





1 +σ





σ

−



σ





1 −σ







(78.142)

Thus, a two-level atom is completely described by the

expectation values

σ

=ρ

−ρ

σ

=ρ

σ

−

=ρ

. (78.143)

Hence the master equation (78.128) can be cast

into the equations of motions for these expectation

values

σ

=−γ



n +



σ

−γ m

∗

σ

−

 ,

Part F 78.8

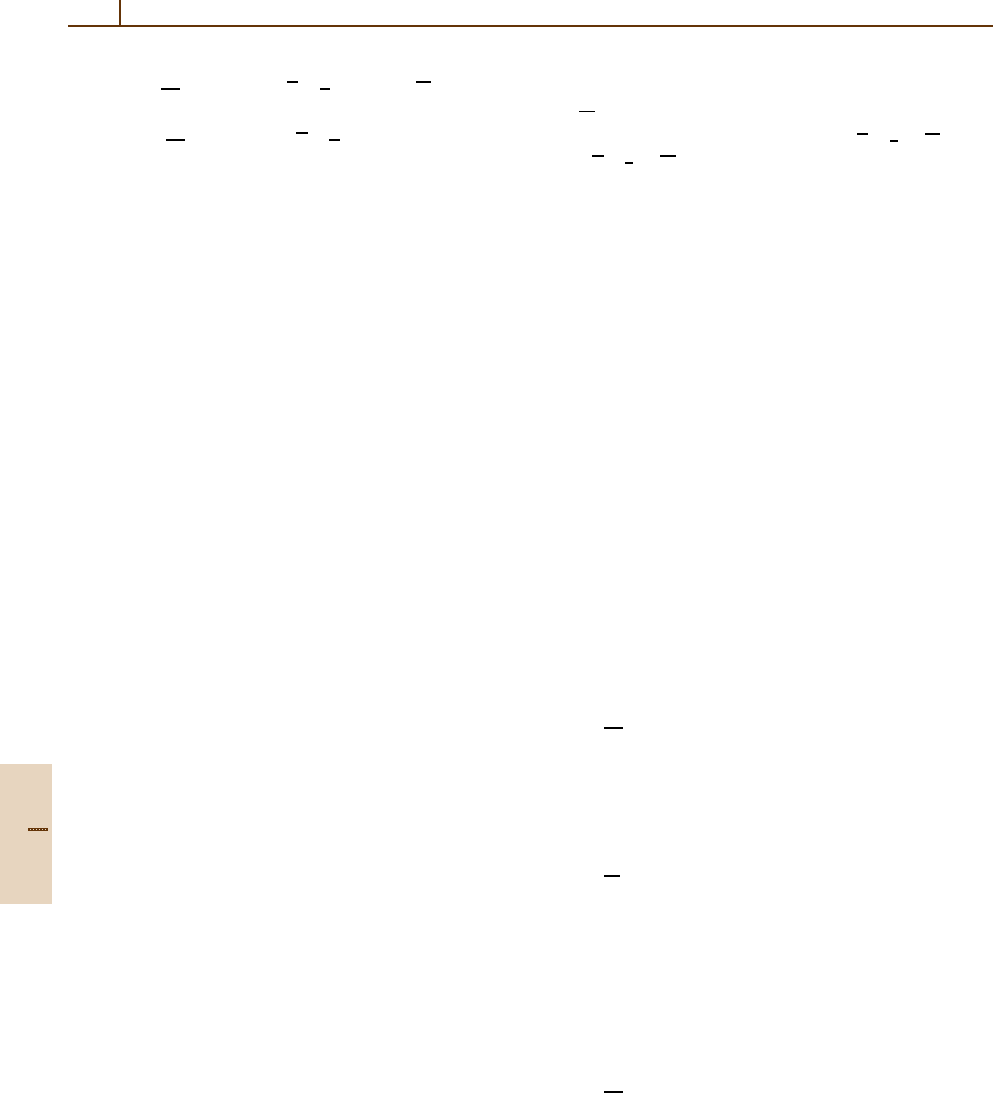
1156 Part F Quantum Optics

σ

−

=−γ



n +



σ

−

−γ mσ

 ,

σ

=−2γ



n +



σ

−γ, (78.144)

which can easily be solved for arbitrary ini-

tial conditions. In contrast to a thermal reservoir

(

m = 0), a squeezed reservoir results in two differ-

ent transverse decay constants γ



n +

+|m|



and



n +

−|m|



[78.34].

78.9 Quantum Regression Hypothesis

In the Schrödinger picture, time-dependent expectation

values for system operators A

can be calculated from

the reduced density operator ρ

(t) via

A

=Tr



(t)



. (78.145)

The reduced density operator, however, is not sufﬁ-

cient to calculate two-time correlation functions such

as A

(t +τ) A

(t). For a deﬁnition of two-time cor-

relation functions, the Heisenberg picture is more

appropriate. Here, expectation values follow from

A

=Tr



†

(t, t

)ρ

)



(78.146)

where U

(t, t

) describes the unitary time evolution of

the complete system and ρ

) is the density operator in

the Heisenberg picture. Similarly, two-time correlation

functions such as A

(t +τ)A

(t) can be deﬁned as

A

(t +τ)A

(t)

= Tr



†

(t +τ, t

)

× U

†

(t, t

)ρ

)



. (78.147)

The quantum regression hypothesis avoids the calcula-

tion of U

(t, t

). Two equivalent formulations exist, one

based on the master equation for ρ

and another based on

the equation of motion for the expectation values A

,

see for example [78.20, 27, 28, 31, 33].

78.9.1 Two-Time Correlation Functions

and Master Equation

It follows from their deﬁnition (78.147)inthe

Heisenberg picture that two-time correlation functions

A

(t +τ)A

(t) for system operators A

and A

can be

calculated with the help of the operator

(t +τ, t) =Tr



(t +τ, t)

× A

(t)U

†

(t +τ, t)



, (78.148)

where U

(t +τ, t) describes the unitary time evolution

of the complete system between t and t +τ.Weﬁnd

A

(t +τ)A

(t)=Tr



(t +τ, t)



. (78.149)

Note, that in (78.148)and(78.149) we interpret A

and

as operators in the Schrödinger picture and have

omitted the argument t

. Because the reduced density

operator

(t) = Tr



(t, t

)ρ

†

(t, t

)



(78.150)

satisﬁes the master equation, it is plausible to assume,

that when the time derivative is taken with respect to τ,

the operator R

(t +τ, t) also satisﬁes the master equation

for ρ

, subject to the initial condition R

(t, t) = A

(t).

However, this requires the additional assumption that

the approximations made in the derivation of the master

equation for ρ

(t) are also valid for R

(t +τ, t).

78.9.2 Two-Time Correlation Functions

and Expectation Values

A second formulation of the quantum regression hy-

pothesis asserts that two-time correlation functions

A

(t +τ)A

(t) obey

∂

∂τ

A

(t +τ)A

(t)





j

(τ)A



(t +τ)A

(t) , (78.151)

provided that the expectation values of a set of system

operators A

satisfy

∂

∂t

A

(t)=





j

(t)A



(t) . (78.152)

This is the form of the quantum regression hypothesis

that was ﬁrst formulated by Lax [78.38].

The equivalence of the two formulations fol-

lows from the interpretation of R

(t +τ, t) on the

right side of (78.149) as a “density operator”. Then



(t +τ, t)



is an “expectation value” for which

we assume that (78.152) is valid; i. e.,

∂

∂τ



(t +τ, t)







j

(τ)Tr





(t +τ, t)



. (78.153)

Accordingto(78.149), this is identical to (78.151).

Part F 78.9

Quantized Field Effects 78.10 Quantum Noise Operators 1157

78.10 Quantum Noise Operators

The master equation is based on the Schrödinger picture

in quantum mechanics: the state of the system described

by a density operator is time-dependent, whereas opera-

tors corresponding to observables are time independent.

If we use the Heisenberg picture instead and make

similar approximations as in the derivation of the mas-

ter equation, we arrive at equations of motion for the

Heisenberg operators, see for example [78.17,28,31,32].

Due to the interaction with a reservoir these equations

have additional noise terms and damping terms.

78.10.1 Quantum Langevin Equations

Again consider a damped harmonic oscillator. The equa-

tion of motion for the annihilation operator

a(t) = e

iω(t−t

)

a(t) (78.154)

in the interaction picture follows from the Heisenberg

equations for the operators a, a

†

, b

and b

†

and reads

=−





−i(ω

−ω)(t−t



)

a(t



) dt



−i



∗

−i(ω

−ω)(t−t

)

). (78.155)

In general, the noise operator

F(t) =−i



∗

−i(ω

−ω)(t−t

)

) (78.156)

is not delta-correlated, and there are also memory ef-

fects in (78.155). The noise operator F(t) can be used to

classify the reservoir: if it is delta-correlated, that is, if

the reservoir has a very broad spectrum, one speaks of

white noise, see below. If the correlation time is ﬁnite

so that there are memory effects, one speaks of colored

noise.

If the spectrum of the noise is very broad (as in

the derivation of the master equation for the reduced

density operator), the operator

a(t) satisﬁes the quantum

Langevin equation

=−

a(t) + F(t),

(78.157)

with a damping term −γ

a(t)/2 and a noise term F(t).

Note that a simple damping equation such as

a(t) =−

a(t)

(78.158)

is unphysical since it does not preserve the commutation

relation



†



= 1. It is the noise term which saves the

commutation relation.

For a thermal reservoir with a sufﬁciently small

correlation time, the standard derivations [78.32]give

F(t)=



†

(t)





F(t)F(t



)





†

(t)F

†



)



= 0 ,



†

(t)F(t



)



= γ nδ(t −t



F(t)F

†



)=γ(n +1)δ(t −t



), (78.159)

where the averages are taken over the reservoir. The

damping constant γ and the number of thermal pho-

tons

n are given in (78.119)and(78.120). For more

general relations, see [78.35, 36], where it is shown

explicitly that correlation functions involving the ﬂuc-

tuation force do not in fact depend on the oscillator

frequency. The condition of a sufﬁciently small reser-

voir correlation time requires that τ

≈ /(k

T ) is small

compared with the time scales of the systems. The

onlytimescalein(78.157)isγ

−1

. The relevant con-

dition is therefore τ

 γ

−1

. For typical applications

in quantum optics, a is the annihilation operator and

†

is the creation operator of a single-mode cavity

ﬁeld. Here one can have quality factors of the cavity

on the order of Q = ω/γ ≈ 10

. In terms of the qual-

ity factor, the condition of sufﬁciently small reservoir

correlation times requires

ω/(k

T )  Q. For optic-

al frequencies



ω ≈3×10

Hz) and T ≈ 300 K one has

ω/(k

T ) ≈75. In the microwave regime (ω ≈30 GHz)

one can have temperatures as low as T ≈ 3mK and

still have

ω/(k

T ) ≈ 75. Therefore the assumption

of delta-correlated noise is a good approximation for

typical applications in quantum optics.

Similarly, for a squeezed reservoir one has

F(t)=



†

(t)



= 0 ,

F(t)F(t



)=γ mδ(t −t





†

(t)F

†



)



= γ m

∗

δ(t −t





†

(t)F(t



)



= γ nδ(t −t





F(t)F

†



)



= γ(n +1)δ(t −t



), (78.160)

which gives a quantitative deﬁnition of the parameters

n and m in the master equations (78.121)and(78.128).

Again, a detailed discussion in [78.35, 36]showsthat

correlation functions involving the ﬂuctuation forces do

not depend on the oscillator frequency.

The Langevin equation (78.157) is based on the

use of the approximate Hamiltonian given in (78.116),

Part F 78.10

1158 Part F Quantum Optics

i. e., it is based on the rotating-wave approximation and

the neglect of self-interaction terms. The correspond-

ing Langevin equation for x =

√

/(2mω)



a +a

†



may

be calculated and, not unexpectedly, it disagrees with

the Abraham–Lorentz equation which Ford and O’Con-

nell [78.39] showed could be derived systematically

using the exact Hamiltonian (78.113). In fact, Ford

and O’Connell showed that an improved equation for

the radiating electron (improved in the sense that it

is second-order and is not subject to the analyticity

problems and the problems with runaway solutions

associated with the Abraham–Lorentz equation) may

be obtained by generalizing the Hamiltonian (78.113)

to include electron structure. The implications follow-

ing from these different equations are presently under

study.

78.10.2 Stochastic Differential Equations

In Sect. 78.10.1 we discussed one of the simplest quan-

tum systems with dissipation, the damped harmonic

oscillator. For more complicated systems the noise term

can also contain system operators. In such cases there are

two different ways to interpret the Langevin equation.

In order to give a feeling for the two possible interpreta-

tions, we discuss the one dimensional classical Langevin

equation

= g(x, t) +h(x, t)F(t)

(78.161)

for the stochastic variable x(t) with delta-correlated

noise F(t)F(t



)=δ(t −t



). Due to the singular na-

ture of delta-correlated noise, such a Langevin equation

does not exist from a strictly mathematical point of

view. A mathematically more rigorous treatment is based

on stochastic differential equations [78.27, 28, 37]. The

variable x(t) is said to obey a stochastic differential

equation

dx (t) = g(x, t) dt +h(x , t)F(t) dt

= g(x, t) dt +h(x, t) dW(t),

(78.162)

if, for all times t and t

, x(t) is given by

x (t) = x(t

) +



g(x(t



), t



)dt





h[x(t



), t



]dW(t



). (78.163)

Here the last term is a Riemann–Stieltjes integral deﬁned





x (t



), t





dW(t



)

= lim

n→∞

n−1



i=0

h[x(τ

), τ

]



W(t

i+1

) −W(t

)



(78.164)

where τ

is in the interval (t

, t

i+1

There are two different approaches to such problems:

the Ito approach and the Stratonovich approach. They

differ in the deﬁnition of stochastic integrals.

In the Stratonovich approach, one evaluates



x (τ

), τ



at τ

= (t

i+1

)/2, whereas in the Ito

approach one evaluates h



(x(τ

), τ

)



at τ

= t

.This

slightly different deﬁnition of τ

leads to different results

because, as a consequence of the delta-correlated noise

term, x(t) is not a continuous path. However, there is a re-

lation between the solution of a Stratonovich stochastic

differential equation and an Ito stochastic differential

equation. Suppose x(t) is a solution of the Stratonovich

stochastic differential equation

dx (t) = g(x, t) dt +h(x , t) dW(t).

(78.165)

Then x(t) satisﬁes the Ito stochastic differential equa-

tion

dx (t) =



g(x, t) +

h(x, t)

∂h(x, t)

∂x



+h(x, t) dW(t).

(78.166)

Instead of dealing with stochastic differential

equations, one can derive a Fokker–Planck equation

for the conditional probability P(x , t|x

, t

).Forthe

Stratonovich stochastic differential equation (78.165),

the Fokker–Planck equation is

∂P

∂t

=−

∂

∂x



g(x, t) +

h(x, t)

∂h(x, t)

∂x



∂

∂x

(x, t)P , (78.167)

which takes the form

∂P

∂t

=−

∂

∂x

g(x, t)P +

∂

∂x

(x , t)P , (78.168)

if (78.165) is interpreted as a stochastic differential

equation in the Ito sense.

The two approaches have the following properties:

(i) in most of the models used in physics the Stratonovich

Part F 78.10