Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics

Подождите немного. Документ загружается.

Quantum Degenerate Gases 76.5 Current Active Topics 1119

often dissipates by shedding vortices when it ﬂows too

fast past an obstacle. It is not clear if the conventional

picture is, or should be expected to be, quantitatively

accurate. In fact, at this time there are no experiments

with alkali vapor condensates in toroidal geometries that

would offer natural conduits for persistent currents.

76.5 Current Active Topics

76.5.1 Atom–Molecule Systems

Diatomic molecules and conversion between atoms and

molecules at temperatures low enough to render the sys-

tem quantum degenerate are at present probably the most

active frontier in the studies of ultracold gases. Experi-

mental achievements include a condensate of molecules,

and coherent transitions between two chemically dif-

ferent species. More broadly, unforeseen new angles

open up into long-standing issues in superﬂuid sys-

tems in condensed matter physics, such as strongly

interacting superﬂuids and BEC-BCS crossover. A snap-

shot of the ﬁeld at this time is given in the present

section.

Two colliding asymptotically free atoms cannot in

general combine into a diatomic molecule, as energy

and momentum would not be conserved in the process.

However, there are two mathematically equivalent meth-

ods to adjust energy conservation, photoassociation and

Feshbach resonance [76.16], both of which may lead to

molecule formation.

The underlying idea is that two seemingly free atoms

may be regarded as a dissociated state of a corres-

ponding diatomic molecule. In photoassociation a laser

drives transitions from a dissociated two-atom state to

a bounded state of the molecule. Energy conservation

is adjusted by tuning the laser. In a Feshbach resonance

hyperﬁne interactions drive transitions from a two-atom

state in a particular manifold of electronic states to a mo-

lecular state in another manifold of electronic states.

The magnetic moments of the two-atom state and the

bounded molecular state are different, so that the res-

onance may be tuned by varying the magnetic ﬁeld

applied on the atom–molecule gas.

Basic Atom–Molecule Model for Bosons. Consider

a minimal model for conversion of bosonic atoms



boson

ﬁeld



into bosonic molecules (

ψ). The Hamiltonian

density reads

†



−

∇



φ +

†



−

∇

+δ



+g(

†

φ +

†

). (76.62)

This model is for free atoms. Atom–molecule coupling

is described as a contact interaction characterized by the

coupling coefﬁcient g. The detuning δ may be adjusted in

photoassociation by tuning the laser, and in a Feshbach

resonance by varying the magnetic ﬁeld.

Effective Scattering Length. Heisenberg equations of

motion for the atomic and molecular ﬁelds read

φ =−

∇

φ +2g

†

ψ,

(76.63)

ψ =



−

∇

+δ



ψ +g

φ. (76.64)

Suppose now that the detuning from resonance, |δ|,is

the largest frequency parameter in the problem, then one

may solve the molecular ﬁeld adiabatically from (76.64)

ψ =−g

φ/δ. Inserting this into (76.63)gives

φ =−

∇

φ −

†

φ, (76.65)

which is the Heisenberg equation of motion for the

atomic ﬁeld that ensues from an effective Hamiltonian

density

†



−

∇



φ +

2π

†

(76.66)

with the effective scattering length

=−

2π δ

(76.67)

Experimentally, the modiﬁcation of the scattering length

is in addition to a constant “background” scattering

length a

, and the sum of the two scattering lengths

a = a

. (76.68)

is usually reported.

As long as one stays sufﬁciently far away from an

atom–molecule resonance, tuning the resonance condi-

tion is tantamount to tuning the atom–atom scattering

length. When the detuning is negative (positive), the en-

ergy of a molecule is lower (higher) than the energy

of an on-threshold pair of atoms, the corresponding in-

duced scattering length is positive (negative), and the

Part F 76.5

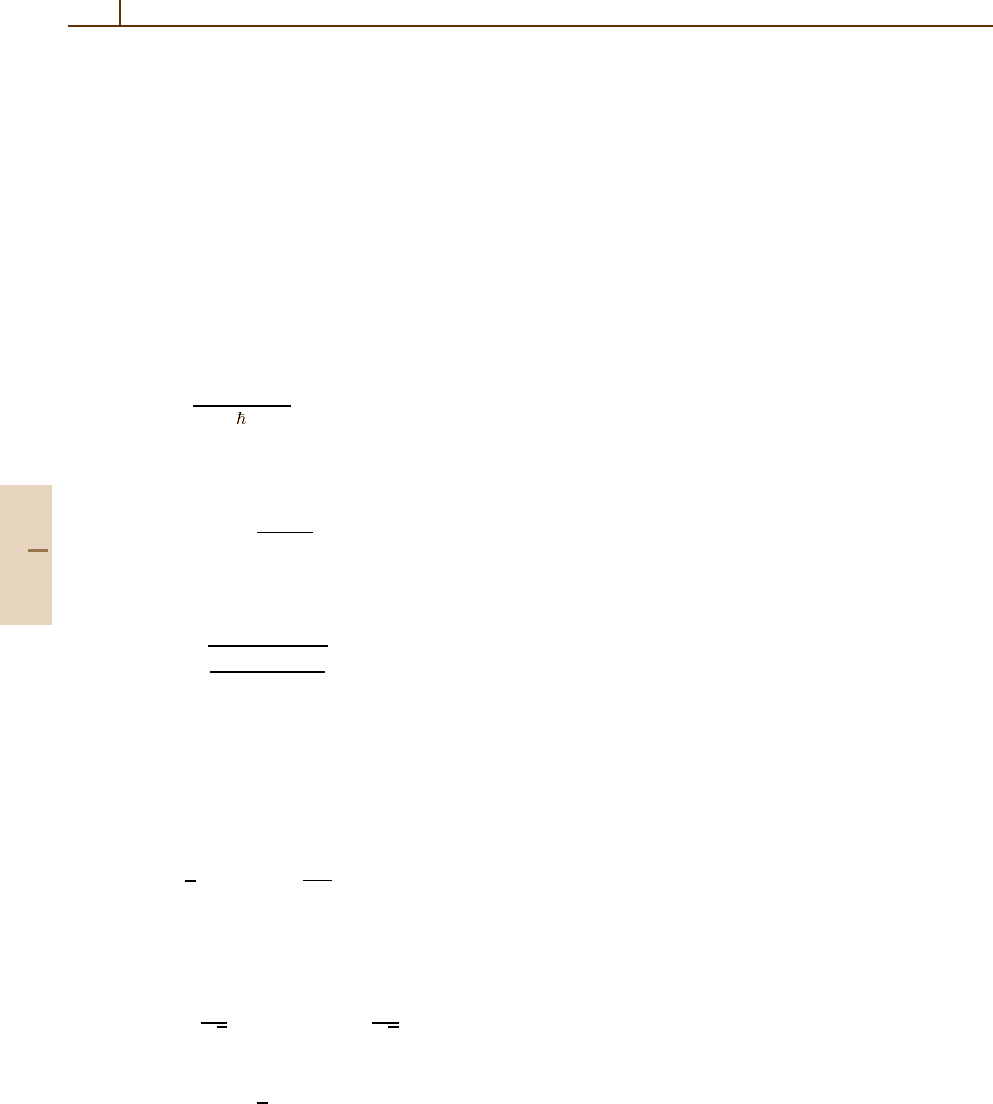
1120 Part F Quantum Optics

induced atom–atom interactions are in effect repulsive

(attractive). It should be noted, though, that the scattering

length does not simply become very large. Vernacu-

lar of this style, and associated attempts to study the

theory of an interacting Bose gas in the limit when

the gas parameter na

is not small, are occasionally

misguided and misleading. The physics rather is in res-

onant, energy-conserving conversion between atoms and

molecules.

Atom–Molecule Coupling Strength. Given the differ-

ence in magnetic moments ∆µ between a molecule

and two atoms and the position of the Feshbach res-

onance B

, the detuning is

δ =

∆µ(B−B

)

. (76.69)

The variation of the scattering length is conventionally

parametrized in terms of the magnetic ﬁeld width of the

Feshbach resonance ∆B as

a = a



1 −

∆B

B− B



(76.70)

A combination of (76.67–76.70) gives the relation

between the ﬁeld width and the contact interaction

parameter characterizing the Feshbach resonance,

g =



2π|a

∆µ ∆B|

(76.71)

Unfortunately, the difference in magnetic moments ∆µ

is not always publicized and one may be forced to

estimate, say, ∆µ ≈µ

Two-Mode Model. Consider next, in the mean-ﬁeld ap-

proximation, the case when only uniform atomic and

molecular condensates are present. The condensates are

represented by complex amplitudes α and β such that

φ →

√

n α and

ψ →

√

n/2 β,wheren now is the invari-

ant density equal to atom density plus twice the density

of the molecules. It follows from (76.63)and(76.64)

that the probability amplitudes for atoms and molecules,

normalized as |α|

+|β|

= 1, satisfy

α =

Ω

√

∗

β, i

β =δβ +

Ω

√

. (76.72)

These are nonlinear variations of the usual two-level

equations (see Chapt. 73) of quantum optics, with the

quantity Ω =

√

ng playing the role of the Rabi fre-

quency. This system displays analogs of coherent optical

transients (see Chapt. 73), such as Rabi oscillations be-

tween atomic and molecular condensates, and adiabatic

following from an atomic condensate to a molecular

condensate when the detuning is swept through the

resonance [76.17].

The two-mode model is simplistic in that it ignores

processes in which molecules dissociate into correlated

pairs of noncondensate atoms [76.18, 19]. There are

also secondary complications. The molecules created in

a Feshbach resonance are highly vibrationally excited,

and tend to get quenched in collisions with atoms and

other molecules. Typical lifetimes are in the millisec-

ond regime. Usual one-color photoassociation from two

atoms to a molecule with the absorption of a photon,

on the other hand, creates an electronically excited mol-

ecule, which decays spontaneously on a time scale far

shorter than the typical photoassociation time scales.

To mitigate spontaneous emission, one usually resorts

to two-color photoassociation, in which a second laser

takes the photoassociated molecules to another more

stable level [76.20].

At present, the two-mode system with just an atomic

and a molecular condensate has never been realized

cleanly in an experiment. Nonetheless, experiments us-

ing a Feshbach resonance have demonstrated Ramsey

fringes in transitions between atomic and molecular

condensates [76.21], and formation of what probably is

a (short-lived) molecular condensate from the bosonic

isotope

Na [76.22].

Fermion Systems. Combining two fermionic atoms

gives a bosonic molecule, and Feshbach resonance in

a Fermi gas is currently a popular topic. The main in-

terest is in the BEC-BCS crossover. Basically, if the

magnetic ﬁeld is tuned so that the detuning is negative,

molecules have a lower energy than atoms. Thermal

equilibration then leads to molecules that will condense

if the temperature is low enough. On the other hand, if

the detuning is positive, atom–atom interactions are at-

tractive. The atoms may undergo a phase transition into

a fermion superﬂuid that is analogous to the BCS phase

transition in a superconductor. What happens in between

has been a question in theory for a while [76.23], and is

ﬁnally accessible to experiments.

Collisionless adiabatic transfer from atoms to

molecules by sweeping the magnetic ﬁeld across a Fesh-

bach resonance works with fermions much like with

bosons [76.24]. Moreover, molecules formed in the

834 G Feshbach resonance in the fermionic isotope

may live for seconds. It is now possible to study ther-

mal equilibrium and long-lived excited states in the

neighborhood of the resonance [76.25–27]. In particu-

lar, the observation of a vortex lattice over a wide range

Part F 76.5

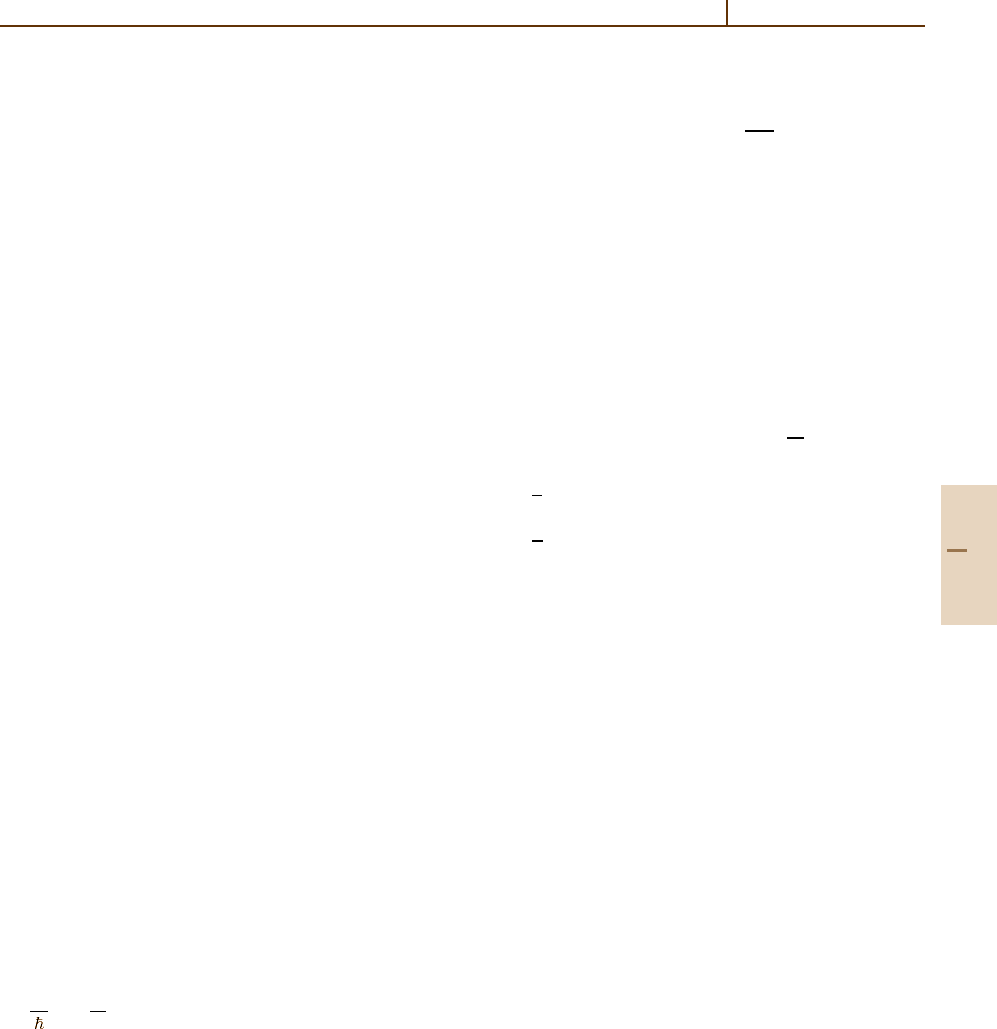
Quantum Degenerate Gases 76.5 Current Active Topics 1121

of magnetic ﬁelds on both sides of the resonance [76.24]

indicates that close to the resonance the gas is a strongly

interacting superﬂuid.

76.5.2 Optical Lattice with a BEC

A BEC conﬁned to a periodic potential enjoys a long-

standing popularity for reasons that have varied in time.

In the early days of BEC the Josephson effect and

phase behavior of a BEC were topical. The possibil-

ity of a quantum phase transition in an optical-lattice

system was the next broad topic to emerge, and nowa-

days speculations about using condensates in a lattice

either as supporting technology or as the active element

in quantum information processing abound. The decep-

tively simple theoretical models of these systems add to

their staying power. In this section, a brief discussion of

an optical lattice holding a BEC is presented. The quan-

tum information view is not pursued here, as so far no

speciﬁc experimental progress has appeared in print.

Optical Lattice. Dipole forces of standing-wave ﬁelds

of light generate a periodic potential, an optical lattice,

on the atoms. If the light is detuned far enough from

atomic resonances, absorption and spontaneous emis-

sion are negligible and the potential is conservative. In

one dimension, the potential energy for the motion of

the atoms is typically of the form

V(x) = V

sin

kx , (76.73)

where k is the wave number of the lattice light, and the

depth of the lattice V

can be inferred from the known

parameters of the atoms and the light as explained in

Sect. 75.2.2.

Double-Well Potential. One can integrate the GPE nu-

merically for an arbitrary potential, but many more

insights have been gained from restricted models. The

simplest one is a double-well potential in the two-state

approximation, in which only the ground state of the

atoms in both wells is taken into account. The Hamilto-

nian is

=−

∆



†



+2κ



†





†





(76.74)

Here ∆ is a parameter characterizing tunneling between

the “left” and the “right” potential well, a

l,r

are the

annihilation operators for ground-state bosons in each

well, and κ is a measure of atom–atom interactions. The

one-particle states in a symmetric double-well poten-

tial with weak tunneling come in doublets, one even

state φ

and one odd state φ

−

, with respect to the cen-

ter of the double-well trap. The choices of signs of the

wave functions are assumed to work out in such a way

that the left and right states are φ

l,r

√

1/2 (φ

±φ

−

Equation (76.74) could be the version of the Hamilto-

nian (76.22) restricted to the basis of the two states φ

l,r

There are many forms of the Hamiltonian (76.74)

that differ by a polynomial of the conserved particle

number

N =



†



. Inasmuch as particle num-

ber is ﬁxed, adding any function of the conserved quan-

tity

N to the Hamiltonian has no effect on the dynamics,

and so such forms are functionally equivalent. Here

polynomials of

N are added to the Hamiltonian without

further notice to produce the simplest-looking results.

Semiclassical Approximation. The usual method of go-

ing to the classical ﬁeld theory gives the equations for

the semiclassical amplitudes deﬁned by a

l,r

√

N →α

l,r

=−

∆ α

+χ|α

=−

∆ α

+χ|α

, (76.75)

with χ = 4κN. Without atom–atom interactions these

are the equations of a resonant two-level system and

describe Josephson oscillations of the atoms between the

sides of the double-well potential. Interactions temper

the oscillations, or stop them completely [76.28].

Phase Diffusion in the Double Well. The model (76.74)

is unusual in that one can easily go beyond the semiclas-

sical approximation [76.29]. The entire state space for

N atoms is spanned by the vectors |n

, n

=|n

, N −n



with n

= 0,... ,N. The Hamiltonian can be diag-

onalized and the time dependence of the system solved

numerically even for large N. Moreover, the common

case in which the atom number ﬂuctuations at the sites

are at least of the order unity, but small in a relative sense,

is amenable to a simple analytical approximation.

The phase difference of the condensates between the

two traps,

ϕ, is a case in point. One can measure it by

releasing the atoms from the trap and letting them inter-

fere. Although there are serious in-principle problems

with this interpretation, phase difference can be viewed

qualitatively as the canonical conjugate of the difference

between the number of atoms on the sides of the double

well,

n ≡

−

, with [

ϕ]=−i. The minimum un-

certainty product of phase difference and atom number

difference is then 1/2. On this basis, results for vari-

ous experiments can be qualitatively and quantitatively

predicted.

Part F 76.5

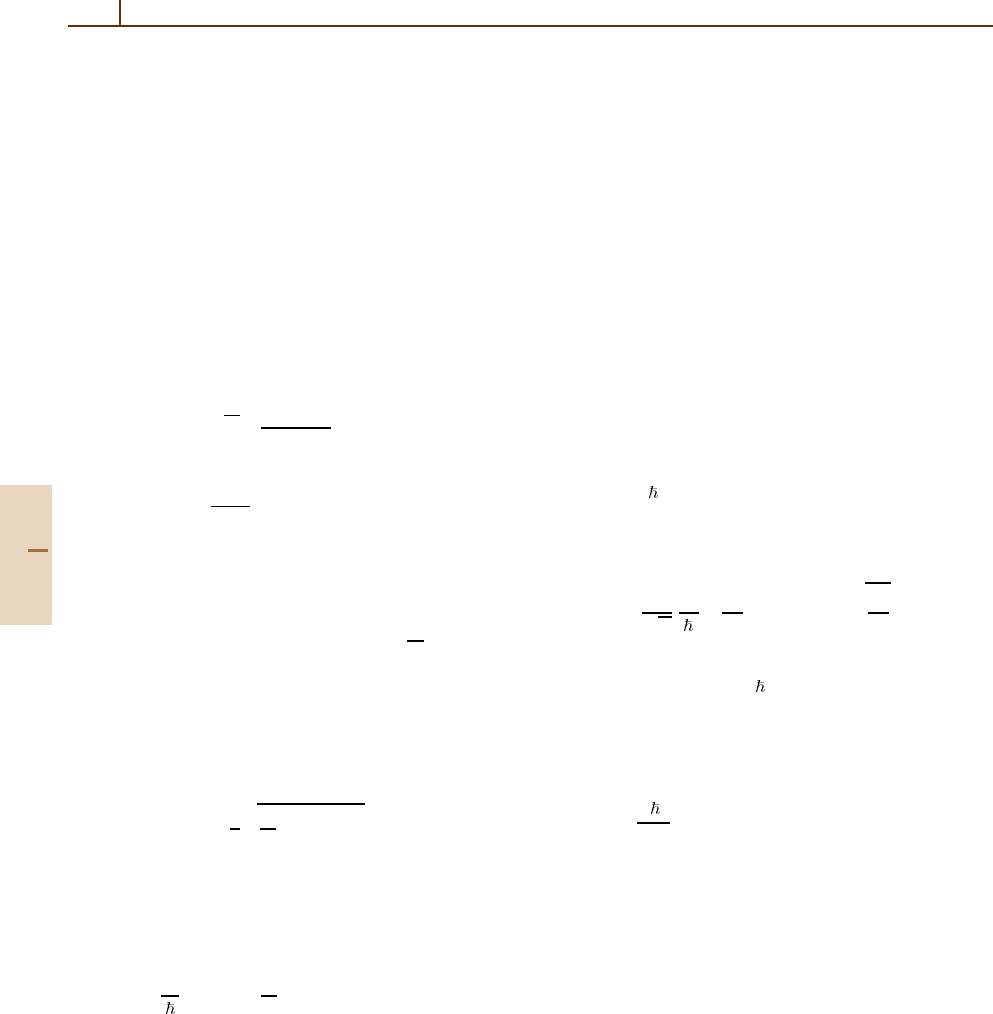
1122 Part F Quantum Optics

For instance, suppose the system is prepared in the

ground state of the Hamiltonian (76.74). The ground

state is an even split of the atoms between the two

traps, but atom number ﬂuctuations depend on the ra-

tio between tunneling and atom–atom interactions. For

|∆|/χ 1, atom–atom interactions dominate, and since

moving an atom from one side of the trap to the other

costs much interaction energy, the ground state is close

to a number state with half of the atoms in each potential

well. In the contrary case, the ground state is essentially

the many-body state with all N atoms in the symmetric

state φ

, which breaks up into a Poissonian distribution

of the atoms between the states φ

and φ

. As long as the

standard deviation of the atom number difference is at

least of the order of unity, it is given by

∆n =

√



∆

∆ +4Nκ



1/4

, (76.76)

and the phase ﬂuctuations are

∆ϕ =

2 ∆n

(76.77)

As discussed above in Sect. 76.3.2, a measurement

of the phase difference will produce a deﬁnite result. In

the interaction-dominated case the result should in effect

be random, while in the tunneling-dominated case the

phase difference should come out the same every time,

save for ﬂuctuations of the order 1/

√

N. Similarly, if one

were to start from the ground state in the case when tun-

neling dominates, and then suddenly turn off tunneling

by adjusting the potential well, atom–atom interactions

would lead to diffusion (or rather, dispersion) of the

phase difference. The result of a phase measurement

becomes increasingly random with time according to

∆ϕ(t) =



+16Nκ

. (76.78)

Bose–Hubbard Model. The corresponding multi-well

problem goes under the rubrics fo the Bose–Hubbard

model and tight-binding approximation. The Hamilto-

nian is





−

∆



†

n+1

†

n−1



+2κ



†





(76.79)

The sum runs over the sites of the optical lattice, which

is taken to be one-dimensional in this example, and

∆ and κ again characterize tunneling and atom–atom

interactions. At the ends of the lattice there are some

boundary conditions, but for a long enough lattice they

do not inﬂuence the physics.

One-particle eigenstates in a periodic lattice are or-

ganized in energy bands, but there is a well-known

transformation in condensed matter physics that makes

orthonormal Wannier states , more or less localized in the

lattice sites, out of the states in each band. The most rig-

orous interpretation of the Hamiltonian (76.79)isthat

it is the representation of the Hamiltonian (76.22)in

the Wannier states belonging to the lowest energy band

of the lattice, ignoring tunneling between non-adjacent

sites. Viewed in this way, the model is only valid in the

limit when the energy per atom for atom–atom interac-

tions is small compared to the energy spacing between

the bands.

Nonetheless, direct integrations of the GPE with

atom–atom interactions also show energy bands, and

for suitably picked parameters the Hamiltonian (76.79)

should be generic for the case when interband transitions

are negligible. Now, without atom–atom interactions the

width of the energy band from the Bose–Hubbard model

would be

∆. On the other hand, the band structure for

the potential energy (76.73) of an optical lattice comes

from the Mathieu equation [76.30]. A comparison gives

the estimate

∆ =

√





3/4

exp



−2





(76.80)

This is an asymptotic expression for the limit when

the recoil energy E

/2m and the lattice depth

satisfy V

 E

. Next suppose that one ascribes to

each potential well the unit-normalized wave function

φ(x), then an estimate for the atom–atom interaction

parameter κ comes from (76.23) in the form

κ =



x |φ(x)|

. (76.81)

Phase Diffusion in the Bose–Hubbard Model. The

dominant feature of the Bose–Hubbard model again is

competition between tunneling and atom–atom interac-

tions. Also, phase and atom number ﬂuctuations may

again be studied analytically under the assumptions that

atom number ﬂuctuations at each site are at least of the

order of unity, but small in a relative sense. For the same

numbers of atoms per site, the results are basically the

same in the two- and multi-well cases.

In fact, multi-well counterparts [76.31]oftheex-

periments on the phase relations are well ahead of the

experiments on two-well systems [76.32]. The multi-

well experiments are in satisfactory agreement with the

theory.

Part F 76.5

Quantum Degenerate Gases References 1123

Superﬂuid-Mott Insulator Transition. Because the size

of the state space tends to grow as L

with the number

of lattice sites L, direct numerical solutions to the multi-

well problem are computationally intractable. This is

somewhat unfortunate, as a long lattice also presents be-

haviors with no obvious analogs in the two-well case,

and for which analytical approximations have proven

hard to come by. When tunneling dominates, the system

is in what is referred to as the superﬂuid phase. Fluctu-

ations of atom number between the states are relatively

large. On the other hand, if atom–atom interactions dom-

inate, it becomes costly in energy to put anything but an

exact number state of atoms at each lattice site. This is

the Mott insulator phase. According to calculations car-

ried out using the so-called Gutzwiller ansatz, the ground

state of an optical lattice inserted in an atom trap con-

sists of regions with the same integer number of atoms

at the lattice sites within each region [76.33]. When the

parameters of the system are varied, in what is known as

a quantum phase transition, the system should abruptly

switch between these phases.

The superﬂuid-Mott insulator transition has been

observed experimentally [76.34]. Lattice parameters, es-

pecially tunneling, can be varied easily by changing the

intensity of the lattice light. The observation of the tran-

sition is by means of phase coherence. In the superﬂuid

state the system is characterized by a global macroscopic

wave function. When the atoms are released from the lat-

tice, atoms originating from different sites are capable

of interference, and the interference pattern reﬂects the

lattice structure. On the other hand, in the Mott insu-

lator phase the lattice sites are in number states with

little phase coherence between them, and there is no

interference pattern.

References

76.1 F. Dalfovo, S. Giorgini, L. P. Pitaevskii, S. Stringari:

Rev. Mod. Phys. 71, 463 (1999)

76.2 A. S. Parkins, D. F. Walls: Phys. Rep. C303,1

(1998)

76.3 A. J. Leggett: Rev. Mod. Phys. 73, 307 (2001)

76.4 S. Stenholm: Phys. Rep. C363, 173 (2002)

76.5 A. L. Fetter: J. Low. Temp. Phys. 129, 263 (2002)

76.6 A. L. Fetter, J. D. Walecka: Quantum Theory of

Many-Particle Systems (McGraw-Hill, New York

1971)

76.7 M. D. Feit, J. A. Fleck Jr., A. Steiger: Solution of

the Schrödinger equation by a spectral method,

J. Comput. Phys. 47, 412 (1982)

76.8 J. R. Schrieffer: Theory of Superconductivity

(Addison-Wesley, Redwood City 1988)

76.9 M. D. Barrett, J. A. Sauer, M. S. Chapman: All-

optical formation of an atomic Bose-Einstein

condensate, Phys. Rev. Lett. 87, 010404 (2001)

76.10 S. Schneider, A. Kasper, Ch. vom Hagen, M. Barten-

stein, B. Engeser, T. Schumm, I. Bar-Joseph,

R. Folman, L. Feenstra, J. Schmiedmayer: Bose-

Einstein condensation in a simple microtrap, Phys.

Rev. A 67, 023612 (2003)

76.11 D. Rychtarik, B. Engeser, H.-C. Nägerl, R. Grimm:

Two-dimensional Bose–Einstein condensate in

an optical surface trap, Phys. Rev. Lett. 92, 173003

(2004)

76.12 B. DeMarco, D. S. Jin: Onset of Fermi degener-

acy in a trapped atomic gas, Science 285, 1703

(1999)

76.13 K. M. O’Hara, S. L. Hemmer, M. E. Gehm, S. R. Gran-

ade, J. E. Thomas: Observation of a strongly

interacting degenerate Fermi gas of atoms, Science

298, 2179 (2002)

76.14 A. G. Truscott, K. E. Strecker, W. I. McAlexander,

G. B. Partridge, R. G. Hulet: Observation of Fermi

pressure in a gas of trapped atoms, Science 291,

2570 (2001)

76.15 J. R. Abo-Shaeer, C. Raman, J. M. Vogels, W. Ket-

terle: Observation of Vortex Lattices in Bose-

Einstein Condensates, Science 292, 476 (2001)

76.16 E. Timmermans, P. Tommasini, M. Hussein,

A. Kerman: Feshbach resonances in atomic

Bose-Einstein condensates, Phys. Rep. C315,199

(1999)

76.17 J. Javanainen, M. Mackie: Coherent photoassocia-

tion of a Bose-Einstein condensate, Phys. Rev. A

59, R3186 (1999)

76.18 S. J. J. M. F. Kokkelmans, M. J. Holland: Ramsey

fringes in a Bose–Einstein condensate between

atoms and molecules, Phys. Rev. Lett. 89,180401

(2002)

76.19 M. Mackie, K.-A. Suominen, J. Javanainen: Mean-

ﬁeld theory of Feshbach-resonant interactions in

Rb condensates, Phys. Rev. Lett. 89,180403

(2002)

76.20 R. Wynar, R. S. Freeland, D. J. Han, C. Ryu,

D. J. Heinzen: Molecules in a Bose-Einstein con-

densate, Science 287, 1016 (2000)

76.21 E. A. Donley, N. R. Claussen, S. T. Thompson,

C. E. Wieman: Atom-molecule coherence in a Bose-

Einstein condensate, Nature 417, 529 (2002)

76.22 K. Xu, T. Mukaiyama, J. R. Abo-Shaeer, J. K. Chin,

D. E. Miller, W. Ketterle: Formation of quantum-

degenerate sodium molecules, Phys. Rev. Lett. 91,

210402 (2003)

76.23 M. Holland, S. J. J. M. F. Kokkelmans, M. L. Chiofalo,

R. Walser: Resonance superﬂuidity in a quantum

Part F 76

1124 Part F Quantum Optics

degenerate Fermi gas, Phys. Rev. Lett. 87,120406

(2001)

76.24 C. A. Regal, C. Ticknor, J. L. Bohn, D. S. Jin: Creation

of ultracold molecules from a Fermi gas of atoms,

Nature 424, 47 (2003)

76.25 S. Jochim, M. Bartenstein, A. Altmeyer, G. Hendl,

S. Riedl, C. Chin, J. Hecker Denschlag, R. Grimm:

Bose–Einstein condensation of molecules, Science

302, 2101 (2003)

76.26 M. W. Zwierlein, C. A. Stan, C. H. Schunck,

S. M. F. Raupach, A. J. Kerman, W. Ketterle: Con-

densation of pairs of fermionic atoms near

a Feshbach resonance, Phys. Rev. Lett. 92,120403

(2004)

76.27 M. W. Zwierlein, J. R. Abo-Shaeer, A. Schirotzek,

C. H. Schunck, W. Ketterle: Vortices and superﬂuid-

ity in a strongly interacting Fermi gas, Nature 435,

1047 (2005)

76.28 S. Raghavan, A. Smerzi, S. Fantoni, S. R. Shenoy:

Coherent oscillations between two weakly coupled

Bose-Einstein condensates: Josephson effects,

π oscillations, and macroscopic quantum self-

trapping, Phys. Rev. A 59, 620 (1999)

76.29 J. Javanainen, M. Yu. Ivanov: Splitting a trap con-

taining a Bose-Einstein condensate: Atom number

ﬂuctuations, Phys. Rev. A 60, 2351 (1999)

76.30 M. Abramowitz, I. A. Stegun: Handbook of Mathe-

matical Functions (Dover, New York 1970)

76.31 C. Orzel, A. K. Tuchman, M. L. Fenselau, M. Yasuda,

M. A. Kasevich: Squeezed states in a Bose-Einstein

condensate, Science 291, 2386 (2001)

76.32 Y. Shin, M. Saba, T. A. Pasquini, W. Ketterle,

D. E. Pritchard, A. E. Leanhardt: Atom interferom-

etry with Bose-Einstein condensates in a double-

well potential, Phys. Rev. Lett. 92, 050405 (2004)

76.33 D. Jaksch, C. Bruder, J. I. Cirac, C. W. Gardiner,

P. Zoller: Cold bosonic atoms in optical lattices,

Phys. Rev. Lett. 81, 3108 (1998)

76.34 M. Greiner, O. Mandel, T. Esslinger, T. W. Hänsch,

I. Bloch: Quantum phase transition from a super-

ﬂuid to a Mott insulator in a gas of ultracold atoms,

Nature 415, 39 (2002)

Part F 76

1125

De Broglie Opt

77. De Broglie Optics

De Broglie optics concerns the propagation

of matter waves, their reﬂection, refraction,

diffraction and interference. The main subﬁelds

of de Broglie optics are electron optics [77.1],

neutron optics [77.2], and atom optics [77.3].

Well-established applications are found in

electron diffraction and microscopy [77.4], electron

holography [77.5], neutron diffraction and

interferometry [77.6]. The subject of atom optics is

relatively new, and applications are currently being

developed in precision spectroscopy, precision

measurement, atom lithography, atom microscopy,

and atom interferometry [77.7–9]. This chapter

concentrates on the principles of de Broglie optics.

Illustrations of these principles will be presented

mainly in the framework of atom optics.

A typical de Broglie optical experiment involves

a source, a beam of particles produced by that

source, an array of optical elements, possibly

a probe, other optical elements placed behind the

probe, and ﬁnally a detector. Optical elements are

collimators, apertures, lenses, mirrors, and beam-

splitters. A probe could be a crystal, a biological

sample, or just another unknown optical element

whose properties are to be investigated.

To avoid proliferation of notation, we refer to

any object placed in the beam path simply as an

“optical element”.

77.1 Overview............................................. 1125

77.2 Hamiltonian of de Broglie Optics .......... 1126

77.2.1 Gravitation and Rotation ........... 1127

77.2.2 Charged Particles ...................... 1127

77.2.3 Neutrons ..................................1127

77.2.4 Spins .......................................1127

77.2.5 Atoms ......................................1127

77.3 Principles of de Broglie Optics .............. 1129

77.3.1 Light Optics Analogy ..................1129

77.3.2 WKB Approximation................... 1130

77.3.3 Phase and Group Velocity........... 1130

77.3.4 Paraxial Approximation ............. 1130

77.3.5 Raman–Nath Approximation ...... 1131

77.4 Refraction and Reﬂection ..................... 1131

77.4.1 Atomic Mirrors ..........................1131

77.4.2 Atomic Cavities .........................1132

77.4.3 Atomic Lenses ...........................1132

77.4.4 Atomic Waveguides ................... 1132

77.5 Diffraction ..........................................1133

77.5.1 Fraunhofer Diffraction ............... 1133

77.5.2 Fresnel Diffraction ..................... 1133

77.5.3 Near-Resonant

Kapitza–Dirac Effect .................. 1133

77.5.4 Atom Beam Splitters ..................1134

77.6 Interference ........................................1135

77.6.1 Interference Phase Shift ............. 1135

77.6.2 Internal State Interferometry ...... 1136

77.6.3 Manipulation of Cavity Fields

by Atom Interferometry.............. 1137

77.7 Coherence of Scalar Matter Waves ......... 1137

77.7.1 Atomic Sources..........................1137

77.7.2 Atom Decoherence .................... 1138

References .................................................. 1139

77.1 Overview

Any collection of particles of mass M and momentum p

has a de Broglie wavelength λ

= 2π / p. Originally

meant to explain the orbits of a single Coulomb-

bound electron, the ultimate wave character of matter

has been conﬁrmed for all fundamental particles, and

also for composite particles such as ions, atoms and

molecules.

In terms of the Bohr radius a

, the ﬁne-structure

constant α, and the electron mass m

2παa



v/c



M/m



= 2π





1/2

(77.1)

Part F 77

1126 Part F Quantum Optics

where v = p/M is the velocity, T =

the kinetic energy, and E

is the atomic unit

of energy (Table 1.4 of Sect. 1.2). For electrons,

≈1.226 426 nm/(T /eV)

1/2

. The thermal de Broglie

wavelength is deﬁned in (77.80).

Regardless of the particle species, the theory of de

Broglie optics divides into two distinct parts: the theory

of dispersion and the theory of the optical phenomena. In

the theory of dispersion an effective Hamiltonian is de-

rived which describes the interaction of the particles with

the optical elements. In the theory of optical phenomena,

the ensuing Schrödinger equation is solved and put into

the context of geometrical and Fourier optics (e.g., by

relating distributions of intensity on the detector screen

to properties of a given optical element).

Dispersion of de Broglie Waves

The theory of dispersion is highly particle speciﬁc,

since it depends on any internal degrees of freedom

which may give rise to permanent magnetic mo-

ments or to induced electromagnetic moments either

in static or in optical light ﬁelds. Interaction with

the latter ﬁelds also may give rise to spontaneous

emission. Spontaneous emission has important conse-

quences for the coherence properties of atomic matter

waves because of the random recoil associated with it

(Chapt. 75).

Dispersion of matter waves differs from that of light

waves in a number of regards. First, the dispersion

relation of free particles is quadratic in the wavenum-

ber giving rise to spatial spreading of wavepackets

even in one-dimensional conﬁgurations. Second, par-

ticles may be brought to rest, which is impossible for

photons. And ﬁnally, particles in beams may show self-

interaction giving rise to nonlinear optical phenomena

even for freely traveling particle waves. Electrons and

ions, for example, experience a particle density depen-

dent Coulomb broadening in the focus of a lens (Boersch

effect [77.5]).

In atom optics, nonlinear phenomena occur due

to atom–atom interactions in the ensemble, the na-

ture of which may be signiﬁcantly inﬂuenced by

laser light [77.10]. In the presence of laser light,

atom–atom interactions mainly result from photon

exchange which, in most cases, leads to a repul-

sive interaction. Details of the microscopic basis

of atom–atom interactions, in particular, those con-

cerning cold collisions, are presented in Sect. 75.5.1.

Characteristic effects of nonlinear atom optics like

four-wave mixing [77.11] and parametric ampliﬁca-

tion [77.12] have been observed with the highly

dense samples provided by Bose–Einstein degenerate

gases (Chapt. 76).

Optics of de Broglie Waves

In contrast to the theory of dispersion, the theory of

optical phenomena of matter waves is quite universal

and bears strong resemblance to ordinary light optics.

This resemblance is closest if the particles can be de-

scribed by a scalar wave function of a structureless

point particle. However, in the presence of resonant laser

ﬁelds, electronic levels, their Zeeman sublevels and pos-

sible hyperﬁne structure may play an important role,

in which case a multicomponent spinor wave function

must be used to describe the atom optical phenomena

properly.

77.2 Hamiltonian of de Broglie Optics

A large class of phenomena of particle optics is well-

described by an effectively one-particle Hamiltonian

model in which the particles are not assumed to mutu-

ally interact. In such a model the ensemble of particles is

described by a wave function ψ(x, t) =x|ψ(t) whose

time evolution is governed by the Schrödinger equation

∂

∂t

|ψ(t)=H(t)|ψ(t)

(77.2)

with a one-particle Hamiltonian of the generic form

H(t) =



p−A(

x, t)



+U(

x, t).

(77.3)

Here,

p and

x denote the canonically conjugate oper-

ators of the center of mass momentum and position,

respectively. The cartesian components of

p and

x obey

the fundamental commutation relation





= i

. (77.4)

The vector potential A(x, t) and scalar potential

U(x, t) account for the interaction of the particle

with all the optical elements, probes, and sam-

ples which are placed between the source and the

detector, including the effects of gravitation and

rotation.

Part F 77.2

De Broglie Optics 77.2 Hamiltonian of de Broglie Optics 1127

77.2.1 Gravitation and Rotation

All particles are subject to the inﬂuence of gravitation

and rotation, which both may be viewed as being special

cases of an accelerated frame of reference. Effects of

uniform gravitation are described by

U(x) =−Mg· x , A(x) = 0 ,

(77.5)

where g describes the direction and magnitude of grav-

itational acceleration. Effects of uniform rotation are

described by

U(x) =−

(

Ω × x

)

, A(x) = M

(

Ω × x

)

(77.6)

where the direction and magnitude of Ω refer to the ori-

entation of the axis of rotation and the angular velocity,

respectively. Here, U(x) is the potential of the centrifu-

gal force while A(x) is the potential of the Coriolis

force.

77.2.2 Charged Particles

The interaction of charged particles (electrons, ions)

with the electromagnetic ﬁeld is described by

U(x, t) = qΦ(x, t), A(x, t) = (q/c)A(x, t),

(77.7)

where q is the particle charge (q =−e for electrons),

and A and Φ denote the gauge potentials of the elec-

tromagnetic ﬁelds E and B, respectively. The ﬁelds are

given by

E(x, t) =−

∂

∂t

A(x, t) −∇Φ(x, t),

(77.8)

B(x, t) =∇× A(x, t). (77.9)

77.2.3 Neutrons

For neutrons interacting with a spatially homogeneous

gas, liquid, or amorphous solid contained in a volume V,

a common model is

U(x) =



inside V ,

0 outside V ,

(77.10)

where U

= 2π

b/M,  being the number density

of scatterers in the volume, and b the bound coherent

scattering length.

For neutrons interacting with perfect crystals, U(x)

is a smooth periodic function with the same periodicity

as the lattice and an average value U

within a single

unit cell (see [77.2] for details).

77.2.4 Spins

The interaction of the spin related magnetic moment µ

with the electromagnetic ﬁeld is described by

U(x, t) =−

µ · B(x, t),

A(x, t) =



µ × E(x, t)



(77.11)

Here, the vector potential is due to the motional cor-

rection of the magnetic dipole interaction. Usually, it is

neglected. However, it does play an important role for

the Aharonov–Casher effect (Sect. 77.7).

For fundamental particles with spin

, one has

µ = g

4Mc

σ ,

(77.12)

where σ is the vector of Pauli matrices, and g is the

g-factor of the particle (Sect. 75.5.2).

Here and in what follows, a hat on U and A indicates

the matrix character of the hatted quantity, the matrix

indices referring to the internal degrees of freedom, like

spin. Similarly, Ψ(x, t) denotes a spinor-valued wave

function. The wave function of a spin-

particle, for

example, is displayed in the form

Ψ(x, t) =



↑

(x, t)

↓

(x, t)



(77.13)

where ψ

↑

(ψ

↓

) is the scalar wave function of the σ

+1(−1) component of the state |Ψ(t).

77.2.5 Atoms

Many optical elements in atom optics are based on the

mechanical effects of the radiation interaction. In the

electric dipole approximation, the interaction of a single

atom with the electromagnetic ﬁeld is described by

U(x, t) =−

d· E(x, t),

A(x, t) = B(x, t) ×

d/c ,

(77.14)

where

d is the operator of electric dipole transition. The

vector potential

A is due to the motional correction of

the electric dipole interaction. Usually it is neglected;

see however, the paragraph Electric Dipole Phase in

Sect. 77.7.

For a monochromatic ﬁeld of frequency ω

E(x, t) = E

(+)

(x)e

−iωt

+h.c., (77.15)

Part F 77.2

1128 Part F Quantum Optics

where E

(+)

(x) deﬁnes both polarization and spatial

characteristics of the ﬁeld. A standing wave laser ﬁeld

with optical axis in the x-direction and linear polariza-

tion , for example, is described by

(+)

(x) =  E

f(x, y, z) cos(kx), (77.16)

where E

is the electric ﬁeld amplitude, k = ω/c is the

wavenumber, and the slowly varying function f(x, y, z)

accounts for the transverse proﬁle of the laser ﬁeld.

The electric dipole operator

d acts in the Hilbert

space of electronic states of the atom. In the particular

case that the polarization of the laser ﬁeld is spatially

uniform and that spontaneous emission does not play

a role, two states are generally sufﬁcient and the atom

may be modeled by a two-level atom with electronic

levels |e and |g of energy E

and E

, respectively

> E

). With the spinor representation

|e=





, |g=





(77.17)

the electric dipole operator assumes the form

d = d 





(77.18)

where d is the matrix element of the dipole transition

and 

denotes its polarization.

The laser ﬁeld is assumed to be near resonant with

the e ↔ gtransition at ω



−E



, and we denote

by ∆ ≡ ω

−ω the atom-laser detuning. Using the rotat-

ing wave approximation (Sect. 68.3.2)inaninteraction

picture with respect to the laser frequency, the Hamilto-

nian describing the atomic dynamics – both internal and

center-of-mass – is given by

H =

−



−∆Ω

(

Ω

†

(

x)∆



(77.19)

where

Ω

(x) = 2d 

· E

(+)

(x)/ (77.20)

is the spatially dependent bare Rabi frequency. In the

ﬁeld (77.16), Ω

(x) is cosinusoidal with peak value

Ω

= 2dE

/ .

Atom Optical Stern–Gerlach Effect

The Hamiltonian (77.19) may be written in the form

H =

σ · B

eff

(

x), (77.21)

where

eff

(x) =



−Re[Ω

(x)], Im[Ω

(x)],∆



. (77.22)

As it stands, the Hamiltonian (77.21) describes the pre-

cession and center of mass motion of a ﬁctitious spin in

an external “magnetic ﬁeld” B

eff

(x). Spatial variations

of this ﬁeld give rise to the Stern–Gerlach effect, i. e.,

the splitting of the atomic center of mass wave function

(see also Sect. 77.5.3).

Adiabatic Approximation

In the position representation, the Hamiltonian (77.19)

acts on state vectors of the form of a bispinor

Ψ(x, t) =



(x, t)



(77.23)

Alternatively, this state vector may be expanded in terms

of the local eigenvectors α

(x), β

(x) of the interaction

matrix, also called dressed states,

Ψ(x, t) = ψ

(x, t)



(x)



+ψ

−

(x, t)



−

(x)

−

(x)



(77.24)

where

U(x)



(x)



=±

Ω(x)



(x)



(77.25)

with eigenvalues determined by the dressed Rabi fre-

quency

Ω(x) =



|Ω

(x)|

+∆

, (77.26)

and coefﬁcients (we suppress the x-dependence for no-

tational clarity)



−





cos

−e

−iϕ

sin

iϕ

sin

cos



≡

S .

(77.27)

Here, the Stückelberg angle ϑ ≡ ϑ(x) and phase angle

ϕ ≡ϕ(x) are deﬁned in terms of the polar representation

of the effective magnetic ﬁeld

eff

= Ω

(

cos ϕ sin ϑ, sin ϕ sin ϑ, cos ϑ

)

. (77.28)

In the dressed state basis, the transformed Hamilto-

nian assumes the form

H ≡

†

S =



p−



Ω(

x)σ

, (77.29)

Part F 77.2