Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics
Подождите немного. Документ загружается.


De Broglie Optics 77.3 Principles of de Broglie Optics 1129
with matrix-valued vector potential
ˆ
A(x) = i
S
†
(x)
[
∇S(x)
]
. (77.30)
This matrix is not diagonal; its off-diagonal elements
describe nonadiabatic transitions between the dressed
states. If the detuning is sufficiently large, and the atom
moves sufficiently slowly, these nonadiabatic transitions
may be neglected in a first approximation. In such an
approximation, which is akin to the Born–Oppenheimer
approximation in molecular physics, the dynamics of
the atom is described by two decoupled Hamiltonians of
the generic form (77.3), with scalar potentials U given
by
U(x) =±
2
Ω(x)
(77.31)
and vector potentials A(x) given by the diagonal elem-
ents of (77.30). The vector potential is usually neglected.
If included, it describes the Berry phase of the mechan-
ical effects of the radiation interaction of a two-level
atom.
The idea behind the adiabatic approximation is that
the internal state of the atom, which is described by
any of the locally varying dressed states, has enough
time to adjust smoothly to the motion of the atom. For
the important case of strong detuning |∆||Ω
1
(x)|,
this assumption is usually well justified. In this case, an
atom in the dressed ground state experiences a potential
which is approximately given by
U(x) =−
|Ω
1
(x)|
2
4∆
.
(77.32)
For red detuning we have ∆>0, in which case the
atom is attracted towards regions of high intensity (high
field seeker). For blue detuning, the atom is repelled
from such regions (low field seeker). A potential sim-
ilar to (77.32) also applies for complex particles like
molecules whose transitions are far detuned from the
light frequency. The potential is proportional to the
dynamic polarizability α(ω) and the field intensity.
Atom Optical Nonlinearity
In very dense atom ensembles at low temperatures, col-
lisions between particles can be described by a contact
interaction whose strength depends, in the simplest case,
on a single parameter, the s-wave scattering length a
(Sect. 75.5.1). In the mean field approximation, these
interactions translate into a density-dependent potential
U(x) =
4π
2
a(N −1)
M
|ψ(x)|
2
, (77.33)
where N is the number of particles. This non-
linearity leads to the occurrence of atom soli-
tons [77.13], four-wave mixing [77.11], and parametric
amplification [77.12].
77.3 Principles of de Broglie Optics
Since the Schrödinger equation is a linear partial dif-
ferential equation, de Broglie optics shares most of
its principles with principles of other wave phenom-
ena, and in particular with the optical principles of
electromagnetic waves.
77.3.1 Light Optics Analogy
The analogy of de Broglie optics and light optics be-
comes particularly transparent for monoenergetic beams
of scalar particles. Such beams are described by a time
harmonic wave function ψ(x, t) = e
−iEt/
ψ
E
(x),where
ψ
E
(x) obeys the stationary Schrödinger equation
Hψ
E
= Eψ
E
. (77.34)
Setting A(x) = 0in(77.3) for simplicity, this equation
assumes the form
∇
2
+
˜
k
2
0
1 −
U(x)
E
ψ
E
(x) = 0 , (77.35)
where the wavenumber
˜
k
0
is related to the energy E via
the dispersion relation
E ≡
2
˜
k
2
0
2M
.
(77.36)
If U = 0 at the entrance to the interaction region, E is
the kinetic energy of the freely traveling de Broglie wave
and
˜
k
0
is the related wavenumber.
Comparing (77.35) with the scalar Helmholtz equa-
tion of electromagnetic theory, and identifying
˜
n
E
(x) ≡
1 −U(x)/E
1/2
(77.37)
as an index of refraction for matter waves, one observes
the complete analogy of scalar optics of stationary matter
waves and monochromatic light waves. This analogy can
be generalized for spinor valued wave functions which
would correspond to vector wave optics in anisotropic
index media. However, in contrast to light, spinor-valued
wave functions do not obey a transversality condition.
Part F 77.3
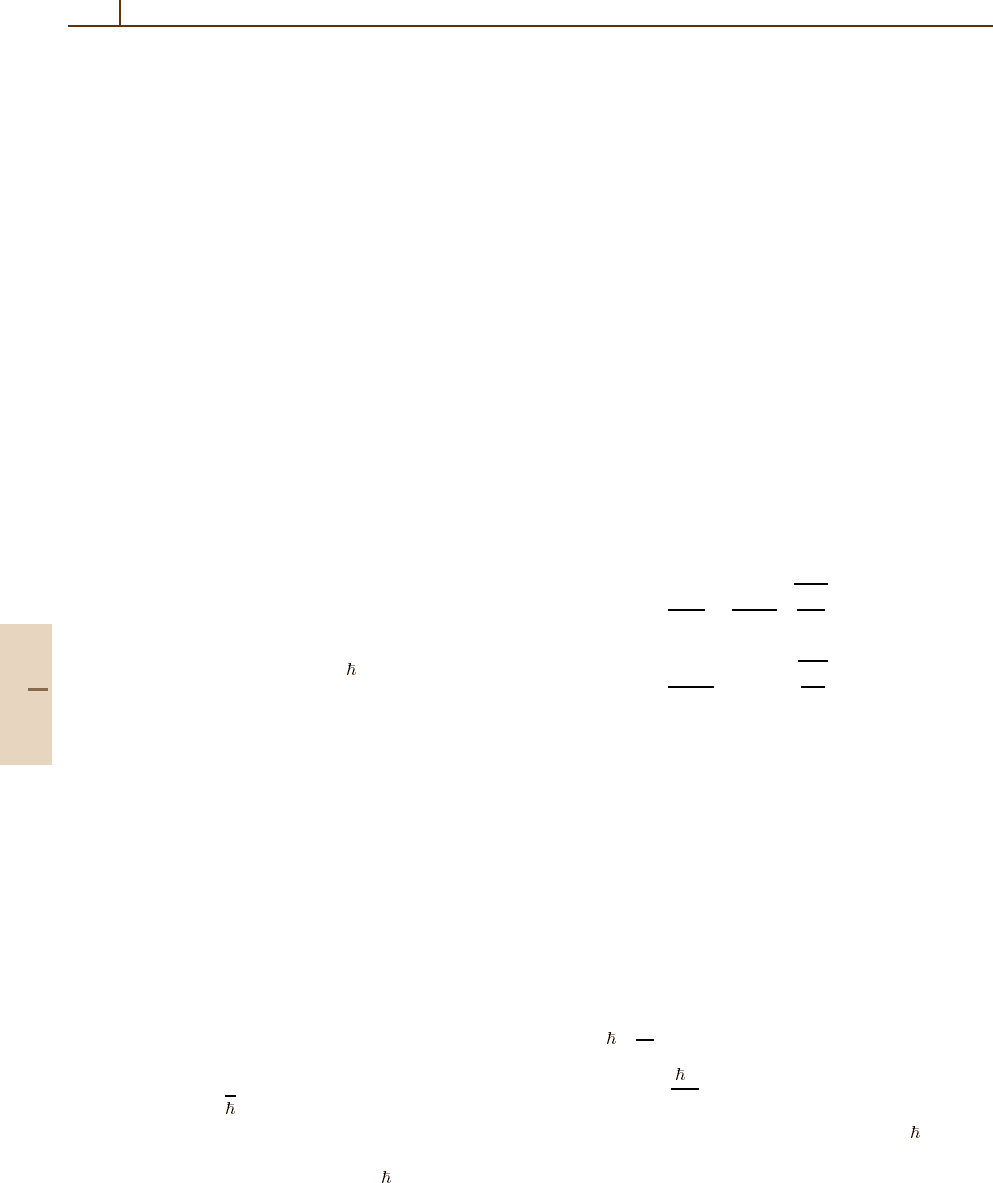
1130 Part F Quantum Optics
In (77.35–77.37), the parameter E describes the kin-
etic energy of the incoming beam. Thus, E is positive,
and therefore
˜
n
E
< 1 for positive values of the poten-
tial, while
˜
n
E
> 1 for negative values of the potential.
For neutrons, one generally has
˜
n
E
< 1. This contrasts
to the index of refraction for light waves which is gener-
ally larger than one. For electrons, ions, and atoms both
˜
n
E
< 1and
˜
n
E
> 1 may be realized.
77.3.2 WKB Approximation
Waves are described by amplitude and phase. Particles
are described by position and momentum. The link be-
tween these concepts is provided by Hamilton’s ray
optics. For scalar matter waves, a ray follows a clas-
sical trajectory. The optical signature of the ray is
the phase associated with it. The quantum mechan-
ical version of Hamilton’s ray optics is obtained in
the WKB approximation of the stationary Schrödinger
equation (77.34).
Any solution of (77.34) may be written in the form
ψ
E
(x) = A(x)e
iW(x)
(77.38)
with real-valued A(x) and W(x).IntheWKB approxi-
mation A(x) ≈ 1, and
W(x) =
˜
k
0
P
P
i
˜
n
E
(s)ds+
−1
x
x
i
A(x
) · dx
,
(77.39)
which is called eikonal in Hamilton’s ray-optics. In
this expression,
˜
n
E
(s) ≡
˜
n
E
(
x(s)
)
,wherex(s) denotes
the classical trajectory of energy E connecting the
point P
i
with the point P, x
i
and x are the coordi-
nates of P
i
and P, respectively, and ds ≡|dx| is the
element of arc length measured along the classical tra-
jectory. Note that the second contribution in (77.39)is
generally gauge-dependent. However, for closed loops
which are frequently encountered in interferometry, the
gauge-dependence disappears by virtue of Stokes the-
orem which transforms the path integral into an area
integral over the rotor of A.
The eikonal (77.39) may also be written in the form
of a reduced action
W(x) =
1
x
x
i
p(x
) · dx
=
x
x
i
˜
k(x
) · dx
, (77.40)
where p(x) is the local value of the canonical momen-
tum of the particle,
˜
k(x) ≡ p(x)/
is the corresponding
wave vector, and the integral is evaluated along the clas-
sical trajectory of the particle. Note that in the presence
of a vector potential, p(x) and dx are no longer parallel
as a result of the difference between canonical momen-
tum p and kinetic momentum M( d/dt) x ≡ p−A.
The WKB approximation becomes invalid in the
vicinity of caustics where neighboring rays intersect.
There, connection formulae are used to find the proper
phase factors picked up by the ray in traversing the caus-
tics. Depending on the topology of the intersecting rays,
different classes of diffraction integrals provide uniform
approximations for the wave amplitude near caustics.
For further details see [77.14] and [77.15].
77.3.3 Phase and Group Velocity
The velocity of a particle which traverses a region of
negative potential increases so that p(x)> p
0
,andthe
phase advances: δW =
[
p(x) − p
0
]
· dx > 0. In quan-
tum mechanics, the classical velocity corresponds to the
group velocity, while the evolution of the phase is de-
termined by the phase velocity. The phase and group
velocities of de Broglie waves are given by
v
p
(x) ≡
E
p(x)
=
1
˜
n
E
(x)
E
2M
,
(77.41)
v
g
(x) ≡
∂E
∂p(x)
=
˜
n
E
(x)
2E
M
,
(77.42)
respectively. Note that the product v
p
v
g
= E/M is inde-
pendent of
˜
n
E
(x).
77.3.4 Paraxial Approximation
The paraxial approximation is useful in describing the
evolution of wave-like properties and/or distortion of
wavefronts in the immediate neighborhood of an optical
ray.
Let the z-axis be the central optical axis of symmetry
along which the optical elements are aligned. Using the
Ansatz ψ
E
(x) = e
i
˜
k
0
z
φ(x, y;z), and dropping ∂
2
φ
∂z
2
in a slowly varying envelope approximation, one obtains
i
v
0
∂
∂z
φ(x, y;z)
=
−
2
2M
∇
2
⊥
+U(x, y;z)
φ(x, y;z), (77.43)
where ∇
2
⊥
= ∂
2
∂x
2
+∂
2
∂y
2
,andv
0
=
˜
k
0
M is
the longitudinal velocity of incoming particles. This
equation has exactly the form of a time-dependent
Part F 77.3
De Broglie Optics 77.4 Refraction and Reflection 1131
Schrödinger equation in two dimensions, with z/v
0
play-
ing the role of a fictitious time t. With this interpretation,
the spatial evolution of phase fronts along z can be an-
alyzed in dynamical terms of particles moving in the
xy-plane.
77.3.5 Raman–Nath Approximation
In the Raman–Nath approximation (RNA) (also called
the short-time, thin-hologram, or thin-lens approxima-
tion), the ∇
2
⊥
term in (77.43) is neglected. The potential
U(x, y;z) then acts as a pure phase structure, and the
solution of (77.43) becomes
φ(x, y;z) =
exp
−
i
v
0
z
z
i
dz
U(x, y;z
)
φ(x, y;z
i
).
(77.44)
In terms of a classical particle moving under the in-
fluence of U, the approximation loses validity for
1
2
Mv
2
⊥
U, which is just a quarter cycle for a harmonic
oscillator.
77.4 Refraction and Reflection
Consider a particle beam of energy E incident on
a medium with constant index of refraction
˜
n
E
.The
boundary plane at z = 0inFig.77.1 divides the vacuum
from the medium. At the boundary, the beam is par-
tially reflected and partially transmitted, with the angles
determined by Snell’s law of refraction
sin α =
˜
n
E
sin β, (77.45)
and the law of reflection
α = α
. (77.46)
The coefficients of reflectivity
˜
R, and transmittivity
˜
T = 1 −
˜
R are given by the Fresnel formula
˜
R =
cos α −
˜
n
E
cos β
cos α +
˜
n
E
cos β
2
. (77.47)
For
˜
n
E
> 1, the interface is “attractive” and
˜
R 1,
with
˜
R → 1 only for glancing incidence α →π/2. For
˜
n
E
< 1, the interface is “repulsive” and total reflection
z
β
α
α⬘
U ⬎ 0
Fig. 77.1 Reflection geometry
˜
R = 1
occurs for α ≥
˜
α
c
,where
˜
α
c
= sin
−1
˜
n
E
is the
critical angle. For α>
˜
α
c
, the de Broglie wave becomes
evanescent, with ψ
E
(z > 0) ∼ e
−
˜
κz
inside the medium
(z > 0), where
˜
κ =
˜
k
0
sin
2
α −sin
2
˜
α
c
1/2
. (77.48)
For thermal neutrons, π/2 −
˜
α
c
∼ 3×10
−3
radians.
If E < U,then
˜
n
E
is imaginary and total reflec-
tion occurs for all α. In neutron optics, this total mirror
reflection requires ultracold neutrons (T ≈ 0.5mK). It
has important applications for storage of ultracold neu-
trons in material cavities, and neutron microscopy using
spherical mirrors. For details see [77.2].
77.4.1 Atomic Mirrors
Inelastic processes, such as diffuse scattering and ab-
sorption, inhibit coherent reflection of atoms from bare
surfaces. The surface must therefore be coated either
with material of low adsorptivity (noble gas, see [77.16])
or electromagnetic fields (evanescent light or magnetic
fields, see below).
Reflection of Atoms by Evanescent Laser Light
Evanescent light fields are produced by total inter-
nal reflection of a light beam at a dielectric–vacuum
interface [77.17]. In the vacuum, the field decays ex-
ponentially away from the interface on a characteristic
length κ
−1
where
κ = k
n
2
sin
2
θ
i
−1
1/2
. (77.49)
Here, n is the light index of refraction of the dielectric,
k is the wave number of the light beam in vacuo, and θ
i
is its angle of incidence.
Part F 77.4

1132 Part F Quantum Optics
If the light is blue-detuned from the atomic res-
onance, an incident beam of ground state atoms
experiences the repulsive potential
U(x) =
2
Ω
0
2
e
−2κ|z|
+∆
2
1/2
−|∆|
.
(77.50)
For α>
˜
α
c
, the evanescent field acts as a nearly
perfect mirror, the imperfections being due to nonadi-
abatic transitions into the “wrong” dressed state, and
possible spontaneous emission. Reflection of atoms
by evanescent laser light was demonstrated by Ba-
lykin et al. [77.18] at grazing incidence and by Kasevich
et al. [77.19] at normal incidence.
Reflection of Atoms by Magnetic Near Fields
Magnetic near fields are produced above substrates with
a spatially modulated permanent magnetization or close
to arrays of stationary currents. In the vacuum above
the substrate, the field decays approximately exponen-
tially over a length comparable to the scale of the
magnetic modulation. The motion of atoms that cross
such inhomogeneous magnetic fields sufficiently slowly
is governed by the analog of the adiabatic potential
described in Sect. 77.2.5:
U(x) =−µ
m
s
/s
B(x)
, (77.51)
where µ is the magnetic moment and m
s
is the (con-
served) projection of the atomic spin s onto the local
magnetic field direction. A repulsive mirror potential is
achieved for spin states with µm
s
< 0; these weak field
seekers are repelled from the strong fields close to the
substrate.
Experiments have used magnetic recording media
like magnetic tapes or hard disks [77.20], arrays of
current-carrying wires [77.21], or amorphous magnetic
substrates [77.22].
77.4.2 Atomic Cavities
Atomic reflections are used in the two kinds of cavities
proposed so far: the trampoline cavity and the Fabry–
Perot resonator.
The trampoline cavity, also called the gravito-optical
cavity, consists of a single evanescent mirror facing up-
wards, the second mirror being provided by gravitation.
A stable cavity is realized with the evanescent laser field
of a parabolically shaped dielectric–vacuum interface,
see [77.23] and the experiment by Aminoff et al. [77.24].
A cavity with transverse confinement provided by a hol-
low blue-detuned laser beam has been demonstrated by
Hammes et al. [77.25].
In the atomic Fabry–Perot resonator both mirrors are
realized by laser light [77.26].
77.4.3 Atomic Lenses
De Broglie waves may be focused by refraction from
a parabolic potential or by diffraction, e.g., by a Fres-
nel zone plate (Sect. 77.5.2). Consider focusing by the
parabolic potential
U(x, y;z) =
1
2
Mω
2
f
(x
2
+y
2
),−w ≤ z ≤ 0
0 , otherwise .
(77.52)
For ground state atoms, such a potential is realized in
the vicinity of the node of a blue detuned standing wave
laser field of transverse width w. In this case
ω
f
= Ω
0
ω
rec
/|∆|
1/2
, (77.53)
where ω
rec
= k
2
2M is the recoil frequency.
Comparison with the Raman–Nath approxima-
tion (77.44)atz =0, with the phase fronts of a spherical
wave converging towards a point x
f
= (0, 0, f ),shows
that U describes a lens of focal length
f =
v
2
0
wω
2
f
. (77.54)
The Raman–Nath approximation is only valid for a thin
lens w f , and breaks down for w>w
RN
=πv
0
/2ω
f
.
In the latter case, oscillations of the particles in the
harmonic potential become relevant, a phenomenon
sometimes called channeling. Channeling may be used
to realize thick lenses with focal length f = w
RN
cor-
responding to a quarter oscillation period.
Focusing of a metastable helium beam using the
anti-node of a large period standing wave laser field
has been demonstrated [77.27]. Such a field is produced
by reflecting a laser beam from a mirror under glancing
incidence. The standing wave forms normal to the mirror
surface. Similar interference patterns provide arrays of
thick lenses that have been exploited in atom lithography
to focus an atomic beam onto a substrate [77.28].
77.4.4 Atomic Waveguides
Atomic waveguides can be realized with potentials that
confine atoms in one or two dimensions [77.29–31].
These devices are key elements for integrated atom
Part F 77.4
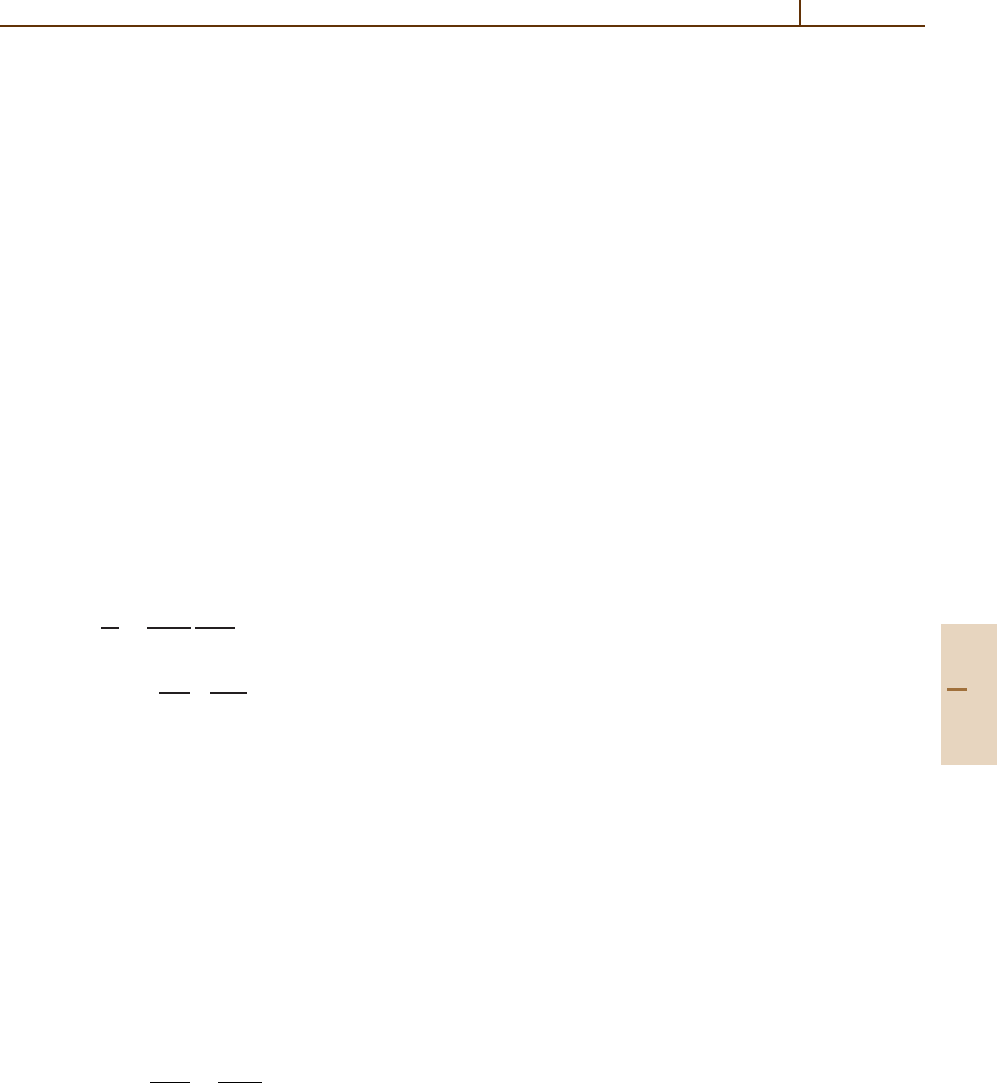
De Broglie Optics 77.5 Diffraction 1133
optics, a field that has seen a rapid evolution re-
cently [77.32, 33]. A planar waveguide is provided by
the one-dimensional confinement in an optical standing
wave [77.34] or an atomic mirror combined with grav-
ity [77.31]. The discrete nature of the waveguide modes
in that case could be demonstrated by lowering the am-
plitude of the confining potential. Linear waveguides can
be modeled by the parabolic transverse potential (77.52)
that now extends along the waveguide axis (the z-
axis). Physical realizations include hollow, blue-detuned
laser beams [77.30], hollow fibers whose inner wall is
coated with blue-detuned evanescent light [77.35], elon-
gated foci of red-detuned light created by cylindrical
lenses [77.36], and magnetic field minima along current-
carrying wires, possibly combined with homogeneous
bias fields [77.37]. With typical thermal atomic ensem-
bles, these waveguides operate in a multimode regime,
and coherent operation has been demonstrated only with
Bose–Einstein condensates. A strong transverse con-
finement that facilitates monomode operation, can be
achieved with miniaturized wire networks deposited on
a solid substrate [77.38, 39]. This approach may lead
to the fabrication of atom chips [77.33]. Even mul-
timode waveguides, however, can yield robust atomic
interferometers, as suggested theoretically in [77.40]
and [77.41].
77.5 Diffraction
The diffraction of matter waves is described by the so-
lution of the Schrödinger equation (77.34) subject to
the boundary conditions imposed by the diffracting ob-
ject. For a plane screen Σ made of opaque portions
and apertures, the solution in the source-free region be-
hind the screen is given by the Rayleigh–Sommerfeld
formulation of the Huygens principle
ψ
E
(x) =
˜
k
0
i
Σ
dξ dη
2π
e
i
˜
k
0
R
R
×
1 +
i
˜
k
0
R
n· R
R
ψ(ξ) ,
(77.55)
where ξ = (ξ,η,ζ) denotes coordinates of points on Σ,
n is an inwardly directed normal to Σ at a point ξ,and
R= x−ξ.
A diffraction pattern only becomes manifest in the
diffraction limit r d,wherer is the distance to the
observation point, and dis the length scale of the diffract-
ing system. The two diffraction regimes are then the
Fraunhofer limit r d
2
/λ
dB
and the Fresnel regime
r ≈ d
2
/λ
dB
, also called near-field optics.
77.5.1 Fraunhofer Diffraction
In the Fraunhofer limit, the field at position (x, y) on
a screen at a distance L downstream from the diffracting
object is given by
ψ(x, y; L) =
˜
k
0
e
ik
0
L
iL
dξ dη
2π
×e
−i(
˜
k
x
ξ+
˜
k
y
η)
ψ(ξ, η;0), (77.56)
where
˜
k
x
=
˜
k
0
x /L,
˜
k
y
=
˜
k
0
y/L. The field at the obser-
vation screen is thus given by the Fourier transform of
the field in the object plane; i. e. the momentum repre-
sentation of the diffracted state. Since most diffraction
experiments in atom optics are performed in the Fraun-
hofer limit, most calculations are done in the momentum
representation.
Atomic diffractions from microfabricated transmis-
sion gratings [77.42] and double slits [77.43] have been
observed. Recent experiments have extended de Broglie
wave diffraction to heavier, complex particles like fuller-
ence molecules (C
60
) [77.44].
77.5.2 Fresnel Diffraction
Typical applications of Fresnel diffraction are Fresnel
zone plates and the effects of Talbot and Lau. Fresnel
zone plates are microfabricated concentric amplitude
structures which act like lenses. They are frequently
employed in optics of α-particles and neutrons. In atom
optics, focusing with a Fresnel zone plate was first
demonstrated by Carnal et al. [77.45].
The Talbot effect and the related Lau effect refer
to the self-imaging of a grating of period d,which
appears downstream at distances that are integral multi-
ples of the Talbot length L = 2d
2
/λ
dB
. For a discrete
set of smaller distances than the Talbot length, im-
ages of the grating appear with smaller periods d/n,
n = 2, 3 ···. For applications in matter wave interfer-
ometry, [77.46]; for applications in atom lithography
see [77.47].
77.5.3 Near-Resonant Kapitza–Dirac Effect
The near resonant Kapitza–Dirac effect refers to the
diffraction of two-level atoms from a standing wave laser
Part F 77.5
1134 Part F Quantum Optics
field with a spatially uniform polarization. The dynam-
ics of the effect is described by the Hamiltonian (77.19)
with the mode function of the laser field given by (77.16).
Consider atoms traveling predominantly in the z-
direction, i. e., orthogonal to the axis of the laser field,
with energy
1
2
Mv
2
0
Ω
0
(Fig. 77.2). Kapitza–Dirac
diffraction is then observed in transmission, which in
the theory of diffraction is called Laue geometry. In the
paraxial approximation (Sect. 77.3.4) for motion in the
z-direction, and assuming that the laser profile is homo-
geneous in the y-direction, the description reduces to
an effectively one-dimensional model for the quantum
mechanical motion along the x-axis of the laser field.
Due to the periodicity of the standing wave light
field, the transverse momenta of the transmitted atom
waves differ by multiples of
k from the transverse
momentum of the undiffracted wave. For the important
case of strong detuning, and assuming that the incoming
atoms are in their electronic ground state moving with
transverse momentum p
x
=0, the p
x
-distribution of the
outgoing wave is given in the Raman–Nath approxima-
tion (Sect. 77.3.5)by
Prob(p
x
= 2n k) ∝
J
n
Ω
0
2
8|∆|
τ
2
, (77.57)
where J
n
is a Bessel function of order n, τ = w/v
0
is an effective interaction time, w being the width of
the laser field, and v
0
the longitudinal velocity of the
atoms. The distribution (77.57) was observed by Gould
et al. [77.48].
For τ
τ
RN
,whereτ
RN
=
ω
rec
Ω
0
2
/|∆|
−1/2
,the
Raman–Nath approximation becomes invalid. As a re-
sult of Doppler related phase-mismatch, the momentum
spread saturates and shows a sequence of collapse and
revival as a function of τ [77.49].
If the detuning is too small to allow for a scalar de-
scription, the two-level character of the atoms must be
taken into account. For the particular case of ∆ = 0,
the ground state evolves into an equal superposition
of the two diabatic states 1
√
2
|e±|g
while enter-
ing the interaction region. Inside the interaction region,
these states experience potentials which differ only
by their sign. For atomic beams with a small spatial
spread δx 2π/k, the diabatic states experience oppo-
site forces, leading to a splitting of the atomic beam
called the atom-optical Stern–Gerlach effect [77.50].
In the general case of arbitrary ∆, the Kapitza–
Dirac Hamiltonian (77.21) is most conveniently
analyzed using band theoretical methods of solid state
theory [77.51].
w
x
z
k
0
Fig. 77.2 Geometry of the Kapitza–Dirac effect
77.5.4 Atom Beam Splitters
Beam splitters are optical devices which divide an in-
coming beam into two outgoing beams traveling in
different directions. For thermal neutrons, beam split-
ters may be realized by diffraction from perfect crystals
in Laue geometry. For atoms, they can be realized using
diffraction from crystalline surfaces, microfabricated
structures (see Sect. 77.5.1), or by using diffraction from
an optical standing wave.
The Kapitza–Dirac effect, for example, may be ex-
ploited to split an atomic beam coherently using Bragg
reflection at the “lattice planes” provided by the pe-
riodic intensity variations of a standing wave laser
field [77.52]. This process is resonant for an incom-
ing atomic beam traveling with transverse momentum
p
x
= k because it is energetically degenerate with
the diffracted beam traveling with transverse momen-
tum
¯
p
x
=− k. This level degeneracy is lifted while
the atoms enter the interaction region. In the Bragg
regime, the lifting happens slowly enough that only
the momentum states |±
k participate in the diffrac-
tion (two-beam resonance), and their populations show
Pendellösung type oscillations as a function of the tran-
sit time. The frequency of the oscillations is given
by δE/
,whereδE is the energy splitting of the
two beams inside the interaction region. For a transit
time giv en by a quarter period of the Pendellösung,
a 50% beam splitting is observed [77.52]. In princi-
ple, Bragg resonances may also be realized for higher
diffraction order p
x
= n k ↔
¯
p
x
=−n k.However,
in this case, intermediate momentum states become
populated (multibeam resonance), which makes the
higher-order Bragg resonances less suitable for beam
splitting purposes.
Part F 77.5
De Broglie Optics 77.6 Interference 1135
More promising for the realization of an atomic
beam splitter is the magneto-optical diffraction which
refers to the diffraction of three-level atoms from a laser
field with a periodic polarization gradient (lin ⊥ lin
configuration) (Chapt. 75), and a magnetic field aligned
parallel to the optical axis of the laser field. This
configuration realizes an interaction potential in the
form of a blazed grating, i. e., a phase grating with
an approximately triangular variation of phase. In an
experiment by Pfau et al. [77.53], transverse split-
ting of a beam of metastable helium by 42
k was
observed [77.49].
Diffraction from an evanescent standing wave
involves Bragg reflection of atoms under glancing
incidence from the periodic grating of a blue de-
tuned evanescent standing wave laser field [77.54–
56]. Diffraction at normal incidence has been
demonstrated with sufficiently slow atoms and can
be described by a generalization of the RNA
(Sect. 77.3.5) [77.57, 58].
77.6 Interference
While the overall phase of a wave function ψ is not ob-
servable, interferometry makes detectable the relative
phases of two components ψ
1
, ψ
2
in a superposition
ψ = ψ
1
+ψ
2
. Two types of interferometers are most
common: the Young double slit as a paradigm for in-
terferometers based on division of wavefront, and the
Mach–Zehnder interferometer as a paradigm for inter-
ferometers based on division of amplitude. In de Broglie
optics, the latter type is realized in the form of a three-
grating interferometer, since division of amplitude is
achieved by diffraction at gratings rather than by semi-
transparent mirrors. Experiments with this geometry
have been reported for atoms [77.59] and recently for
more massive, complex molecules (fullerenes) [77.60].
77.6.1 Interference Phase Shift
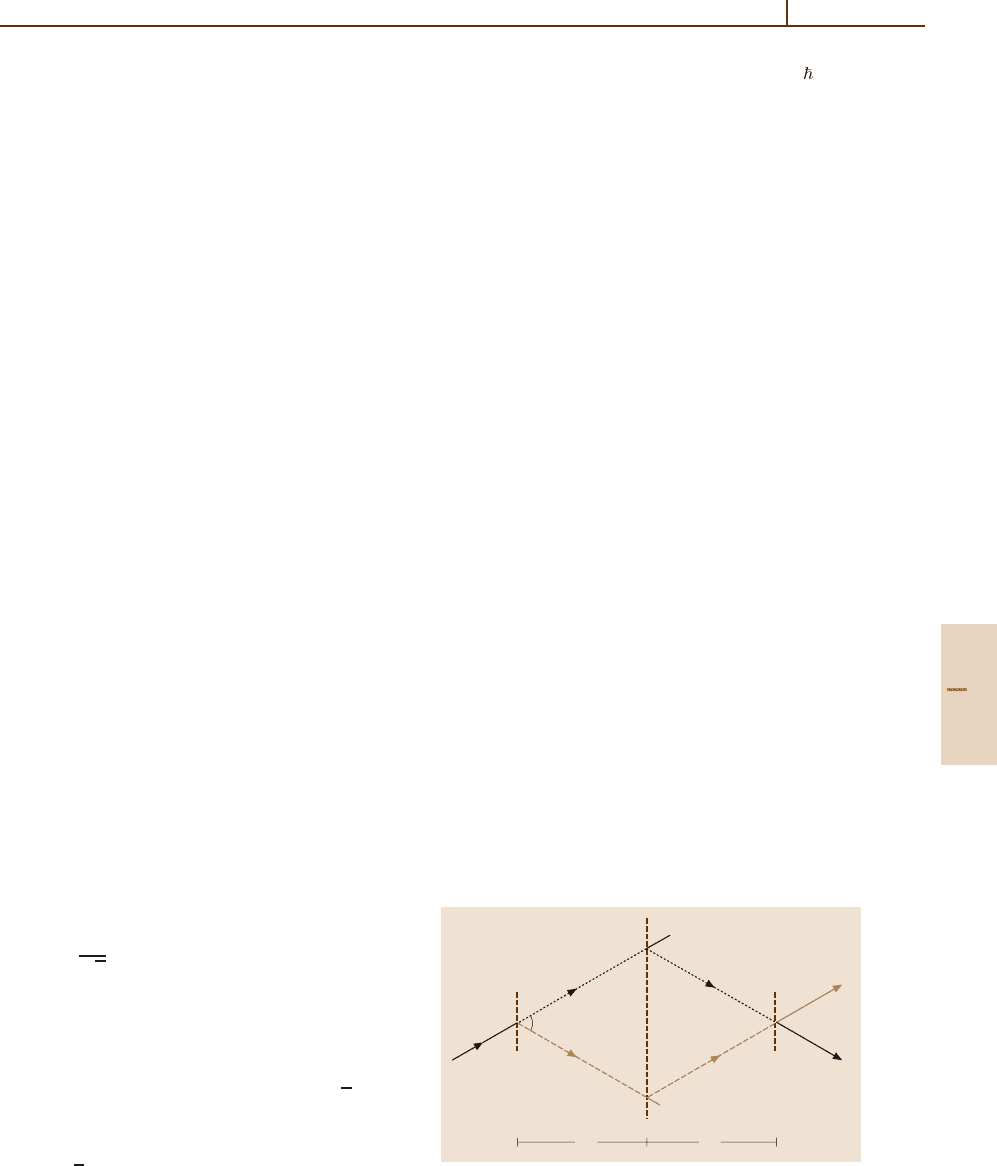
From a fundamental point of view, any interferometer
is a ring. At the entrance port of a three-grating inter-
ferometer displayed in Fig. 77.3, for example, the wave
function is split into two coherent parts which spatially
evolve along different paths and subsequently come to-
gether at the exit port where they are superimposed to
produce two outgoing waves
ψ
±
=
1
√
2
(
ψ
1
±ψ
2
)
,
(77.58)
where the components from path 1 and 2 are given by
ψ
1
= A
1
exp
(
iW
1
)
,
ψ
2
= A
2
exp
(
iW
2
)
.
(77.59)
For simplicity, assume A
1
= A
2
= A
0
√
2. The rel-
ative flux of the outgoing waves is then
I
±
=
1
2
1 ±cos χ
,
(77.60)
where χ =W
1
−W
2
is the relative phase of the two com-
ponents. The sinusoidal variations of I
±
with varying χ
are called interference fringes, and χ/2π is called the
fringe order number.
In the WKB approximation, the phases W
1
and W
2
are given by
W
i
= W
0
+
i
˜
k(x) · dx, i = 1, 2 ,
(77.61)
where the integrals extend over the classical paths 1 and
2, respectively, and dx is an element of displacement
along the paths. Using (77.61), the relative phase is
χ =
C
˜
k(x) · dx ,
(77.62)
where C is the closed interferometer loop. Note, that on
path 2, the path element dx and
˜
k are antiparallel.
Usually, the absolute value of χ is not measured, but
only variations, called phase shifts, which result from
displacements of the diffraction gratings or placement
of optical elements into the beam path. Phase shifts
DD
υ
Ψ
1
Ψ
2
Ψ
+
Ψ
–
Fig. 77.3 Geometry of the three-grating interferometer
Part F 77.6
1136 Part F Quantum Optics
come in two categories: dispersive and geometric. If
a phase shift χ depends on v
0
, it is called dispersive,
otherwise it is called geometric. Geometric phases de-
pend only on the geometry of the interferometer loop.
The Sagnac effect (see below), for example, may be
geometric. A phase which depends neither on v
0
nor
on the geometry of the interferometer loop is called
topological. The Aharonov–Bohm effect (see below) is
topological.
Using (77.39), χ becomes
χ = χ
0
+χ{U}+χ{A}, (77.63)
where for weak potentials U and A,
χ
0
=
Mv
0
(
L
1
−L
2
)
,
(77.64)
χ{U}=−
1
v
0
U[x(s)]ds ,
(77.65)
χ{A}=
1
A(x) · dx ,
(77.66)
and L
i
is the geometric length of the path i. For a constant
potential U
0
intersecting the interferometer on a length
w, χ{U} is given by
χ{U}=−
U
0
w
v
0
. (77.67)
Using Stokes theorem, χ{A} may be written in the
manifestly gauge-invariant form
χ{A}=
1
[
∇× A(x)
]
· da ,
(77.68)
where the integral extends over the area enclosed by the
interferometer, and da is an infinitesimal area element.
Dispersive Phase Shifts. Atom interferometers have
been able to measure phase shifts of the form (77.65) due
to, for example, the atomic level shift in an electric field
(Stark effect) [77.59] or to coherent forward scattering
by background gas atoms, see (77.10) and [77.61].
Sagnac Effect. The Sagnac effect refers to χ{A}in a ro-
tating interferometer. Inserting (77.6)into(77.68), and
assuming that the axis of rotation is oriented perpendic-
ular to the plane of the interferometer, the Sagnac phase
shift is given by
χ
Sa
= 4MΩA/ , (77.69)
where A is the geometric area enclosed by the inter-
ferometer loop. χ
Sa
may be dispersive or geometric
depending on the type of interferometer. In a Young
double slit, A is independent of energy and χ
Sa
is ge-
ometric. In a three-grating interferometer, the area is
A ≈ ϑD
2
,whereϑ is the splitting angle; see Fig. 77.3.
In this case, χ
Sa
is dispersive because of the velocity
dependence of ϑ ≈ 2
k/Mv
0
. The Sagnac effect for de
Broglie waves was first observed by Werner et al. [77.62]
using a neutron interferometer.
Aharonov–Bohm Effect. The Aharonov–Bohm effect
refers to the χ{A} of charged particles encircling
a magnetic flux line [77.63]. Inserting A from (77.7)
into (77.68), and assuming particles of charge q encir-
cling a line of flux Φ once, one finds
χ
AB
= qΦ/ . (77.70)
A characteristic feature of the Aharonov–Bohm effect is
that the particles actually never “see” the magnetic field
of the flux line which is confined to some region inac-
cessible to the particles. χ
AB
is strictly topological, and
only depends on the linking number of the interferome-
ter loop and the flux line. Its appearance is characteristic
for all gauge theories. For further details and a summary
on its experimental verification see [77.5].
Aharonov–Casher Effect. The Aharonov–Casher ef-
fect refers to χ{A} of a magnetic spin encircling an
electric line charge [77.64]. Inserting A from (77.11)
into (77.68), one obtains for proper alignment of µ
and E
χ
AC
= 2π
|µ|
µ
B
r
0
ξ
,
(77.71)
where r
0
is the classical electron radius, µ
B
is the
Bohr magneton, and ξ = e/ρ
el
, ρ
el
being the electric
line charge density. χ
AC
is topological only if the
spin is aligned parallel to the electric line charge and
both are oriented perpendicular to the plane of the
interferometer. χ
AC
for atoms has been observed by
Sangster et al. [77.65].
Electric Dipole Phase. Electric dipole phase refers to the
χ{A} of an electric dipole moment encircling a mag-
netic line charge [77.66]. Inserting A from (77.14)
into (77.68), one obtains for proper alignment of d and
B
χ
dE
= 2π
|d|
ea
0
a
0
ξ
,
(77.72)
where a
0
is the Bohr radius, and ξ = Φ
0
/
mg
, Φ
0
be-
ing the magnetic flux unit, and
mg
being the magnetic
line charge density. In analogy to the Aharonov–Casher
Part F 77.6
De Broglie Optics 77.7 Coherence of Scalar Matter Waves 1137
effect, χ
dE
is topological, provided that d is aligned par-
allel to the magnetic line charge, and both are oriented
perpendicular to the interferometer plane.
77.6.2 Internal State Interferometry
Manipulation of the internal state of atoms by means
of electromagnetic fields makes it possible to realize in-
terferometric setups which involve separation of paths
in internal space rather than in real space. Examples
of such interferometers are the Optical Ramsey inter-
ferometer [77.67], the stimulated Raman interferometer
[77.68], and the interferometers using static electric and
magnetic fields [77.69, 70].
77.6.3 Manipulation of Cavity Fields
by Atom Interferometry
The entanglement of atomic states and quantized field
states opens novel possibilities for manipulating and/or
measuring nonclassical field states in a cavity. In the
adiabatic limit, for example, and assuming sufficient
detuning between the atom and the cavity field, the in-
teraction and c.m. motion of an atom traversing a cavity
is well described by the potential (77.32)
U(x) =−
g
2
∆
f(x)
2
a
†
a , (77.73)
where g is the vacuum Rabi frequency, f(x) is a cavity
mode function, and a, a
†
denote cavity photon annihila-
tion and creation operators, respectively.
Because of the presence of the photon-number op-
erator a
†
a in (77.73), the deflection and phase shift of
an atom traversing the cavity is quantized, displaying
essentially the photon number statistics in the cavity.
The quantized deflection is sometimes called the inverse
Stern–Gerlach effect.
Due to the entanglement of atom and cavity states,
and the position dependence of the interaction strength,
the phase shift induced by U(x) in a standing wave
cavity may be used to measure either the atomic position
via homodyne detection of the cavity field [77.71, 72],
or the photon statistics via atom interferometry [77.73,
74]. In a ring cavity, the entanglement of c.m. motion
and cavity field may be used to measure the atomic
momentum [77.75] via homodyne detection of the cavity
field. For further details see [77.76]andChapt.78.
77.7 Coherence of Scalar Matter Waves
The general solution of the free Schrödinger equa-
tion (77.2) may be written in the form
ψ(x, t) =
d
3
˜
ka(
˜
k)e
i(
˜
k·x−ω(
˜
k)t)
, (77.74)
where ω(
˜
k) ≡ E/ =
˜
k
2
/2M. If the coefficients a(
˜
k)
are known, the state represented by ψ(x, t) is called
a pure state. Otherwise it is called a mixed state, and
physical quantities are obtained by an ensemble average
over the possible realizations of a(
˜
k).
The degree of coherence of matter waves is described
by the autocorrelation function of Ψ(x, t):
Γ(x, t; x
, t
) ≡ Ψ(x
, t
)
∗
Ψ(x, t), (77.75)
where the overline (···) denotes the ensemble average
over the possible realizations of a(
˜
k). In light optics,
Γ(x, t; x
, t
) is called the mutual coherence function.
In particular, for equal times, Γ(x, t;x
, t) describes the
spatial coherence, and for equal positions, Γ(x, t; x, t
)
describes the temporal coherence.
For a beam of particles, coherence may be either
longitudinal (measured along the beam) or transverse
(measured across the beam). In contrast to light optics,
there is no simple relation between longitudinal coher-
ence and temporal coherence because the dispersion
relation of matter waves is quadratic in the wavenumber.
The spatial coherence function is intimately related
to the quantum mechanical density operator of the par-
ticles (Chapt. 7)
ρ(t) =
|Ψ(t)Ψ(t)| . (77.76)
In the position representation, one has
x|ρ(t)|x
≡ρ(x, x
;t) = Γ(x, t;x
, t). (77.77)
Longitudinal and temporal coherence of a particle
beam is determined mainly by the source of the beam.
The thermal fission reactors used in neutron optics and
the ovens used in atom optics are analogous to black-
body sources in light optics. In contrast, the transverse
coherence is mainly determined by the way the particles
are extracted from the oven to form a beam.
77.7.1 Atomic Sources
To describe thermal sources, consider a single particle
in an ove n of temperature T and volume V, assuming
Part F 77.7

1138 Part F Quantum Optics
that a(
˜
k) and a(
˜
k
) are statistically independent:
a(
˜
k)
∗
a(
˜
k
) = ρ(
˜
k )δ(
˜
k−
˜
k
), (77.78)
where
ρ(
˜
k ) =
λ
3
th
V
exp
−
2
˜
k
2
2Mk
B
T
(77.79)
accounts for the thermal distribution of wavenumbers,
and
λ
th
=
2π
2
Mk
B
T
1/2
(77.80)
denotes the thermal de Broglie wavelength.
Using (77.78)–(77.80)in(77.75), the mutual coher-
ence function becomes
Γ(x, t; x
, t
) =
1
V
1
{
1 +
[
i(t −t
)/τ
th
]
}
3
2
×exp
−π
x−x
2
λ
2
th
(
1 +
[
i(t −t
)/τ
th
]
)
,
(77.81)
where
τ
th
=
k
B
T
,
(77.82)
is the thermal coherence time.
According to (77.81), the spatial coherence of a ther-
mal state falls off in a Gaussian manner on a scale given
by λ
th
. The temporal coherence, in contrast, falls off al-
gebraically on a time scale given by τ
th
. Expressed in
physical units, one has
λ
th
=
1.74( 5) ×10
−9
m
√
(M/u)(T/K)
,
τ
th
=
7.63 × 10
−12
s
(T/K)
,
(77.83)
where u is the atomic mass unit.
Atomic Beams
Effusive Beams. Effusive beams are produced from ther-
mal sources by a suitable set of collimators placed
in front of the opening of the oven. This produces
a Maxwell–Boltzmann distribution of atomic velocities
in the longitudinal direction. The coherence properties in
the transverse direction are described by the van Cittert–
Zernike theorem [77.77]; for details see any textbook on
classical optics.
Supersonic Beams. Supersonic beams are produced by
supersonic expansion of a high pressure gas which is
forced through an appropriately designed nozzle. The
expansion produces a velocity distribution in the longi-
tudinal direction which is approximately Gaussian with
a velocity ratio v/δv ≈ 10–20.
Pulsed Beams. Pulsed beams are produced by chopping
any of the beams described above. Important applica-
tions for pulsed beams are the resolution of temporal
coherence and the mapping of the relative phases of
the a(
˜
k) in matter wave interferometry.
Laser-like Source of Atoms. In these sources, many
atoms with integral spin (Bosons) occupy one and the
same quantum state of motion [77.78]. Their operational
principle is rooted in the quantum statistical effects of in-
distinguishability. It may be viewed in close analogy to
the operational principle of an ordinary laser (Chapt. 70)
and the mechanism underlying Bose–Einstein Conden-
sation (Sect. 76.1.1). Laser-like sources have indeed
been achieved by letting a small current of atoms leak
out of a trapped Bose–Einstein condensate [77.79].
77.7.2 Atom Decoherence
In any interferometer, the contrast of the interference
fringes quantitatively measures the coherence of the
wave involved. Partially coherent beams show an output
flux given by
I
±
=
1
2
1 ±Re
Ce
iχ
,
(77.84)
instead of (77.60), with a complex number C. One has
|C|≤1, with the maximum achieved for a pure state; the
phase of C is measured by scanning the interferometer
phase shift χ.
In de Broglie interferometry, coherence can be lost
when the interfering matter wave gets entangled with
other systems. This happens for atoms, for example,
due to the emission or scattering of photons, as soon
as the detection of these photons permits, in prin-
ciple, the resolution of spatially separated paths in
the interferometer. In fact, the width of Γ(x, t;x
, t)
as a function of x−x
, also called the spatial co-
herence length, is reduced to the photon wavelength
after a single scattering event, see [77.80, 81]. Inter-
ference can be restored when the emitted photons are
detected and correlated with the atom output [77.82,83].
Collisions with background gas atoms between the op-
tical elements of a three-grating interferometer also
Part F 77.7
