Dong S.-H. Wave Equations in Higher Dimensions

Подождите немного. Документ загружается.

184 14 Klein-Gordon Equation with the Coulomb Potential

angular momentum quantum number l are ﬁxed, the energy difference E(n,l,D)

between eigenvalues for dimensions D and D −1 is written as

E(n,l,D)=E(n,l,D) −E(n,l,D −1)

|ξ|





1 +

(σ +

√

−ξ

)

−



1 +

(σ +



−ξ

)



, (14.20)

where

σ =n −l −1/2,κ

=(2l +D −3)/2. (14.21)

It is found from Eq. (14.20) that the relation between E(n,l,D)and the dimension

D is more complicated than that of the Schrödinger equation for the hydrogen atom.

The problem arises from the factor



−ξ

(or



−ξ

). For a bound state, it is

found from Eq. (14.2) that λ has to be a real number. Therefore, for a weak potential,

|ξ|< 1/2, we obtain from Eqs. (14.3) and (14.9)

D =2(1 −l +κ)

⎧

⎪

⎨

⎪

⎩

≥2 +2|ξ |, when l =0 and κ>|ξ|,

≤2 −2|ξ |, when l =0 and κ<−|ξ|,

≥2|ξ |, when l =1,

≥0, when l ≥2.

(14.22)

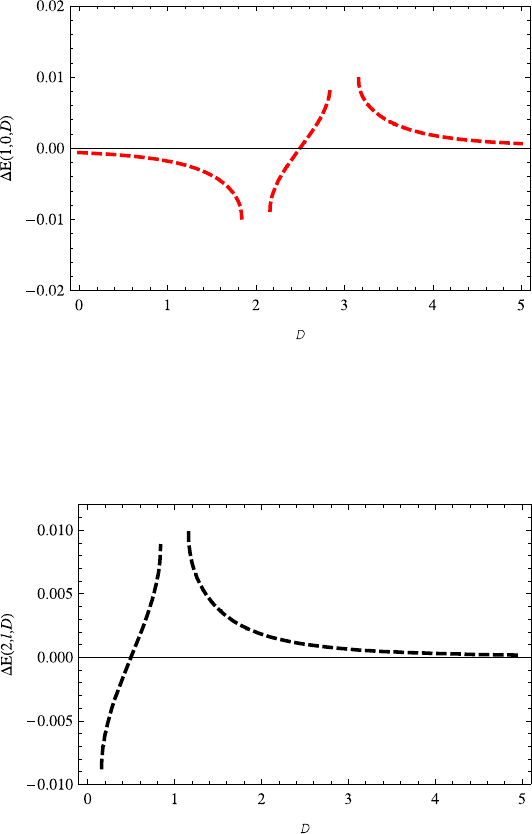
Now, we ﬁrst show the variation of the energy difference E(n,l,D) on the di-

mension D in Figs. 14.1, 14.2, 14.3. We take the parameters M =1 and ξ =11

/137

(Z =11) for deﬁniteness. Recall that the energy and ξ has the same sign as shown

in Eq. (14.15). These three ﬁgures display three typical variations of E(n,l,D)

on D.

It is shown from Fig. 14.1 that there exist two singular points at D ∼2 and D ∼3

for E(1, 0,D). As the dimension D increases, the energy difference E(1, 0,D)

ﬁrst decreases with the dimension D in the region (0, 1.8] and then increases with

the dimension D in the region [2.2, 2.8], and ﬁnally decreases again with the di-

mension D ≥ 3.2. Recall that the variant range of dimension D is related with the

parameter ξ as shown in Eq. (14.22). The variation of E(2, 0,D)on the dimension

D is very similar to E(1, 0,D). We do not show E(2, 0,D) for simplicity. In

Fig. 14.2 we ﬁnd that there exists one singular point near D =1for

E(2, 1,D).As

the dimension D increases, the energy difference E(2, 1,D) ﬁrst increases with

the dimension D and then decreases with it. We show the E(3,l,D) (l =2, 1, 0)

in Fig. 14.3. Notice that the energy difference E(3, 2,D) decreases monotoni-

cally as the dimension D increases. In particular, it is found that E(n, 0,D) is

symmetrical with respect to point (2.5, 0).

Second, we analyze the variations of the energy E(n,l,D) on the dimension D

in Figs. 14.4, 14.5, 14.6. First of all, we emphasize that there is no bound state for s

wave (l =0) in two-dimensional space D =2, because from Eqs. (14.3) and (14.2)

we ﬁnd that κ = 0 and λ is imaginary. Notice that if the two-dimensional space is

considered as a special case of three-dimensional space where all physical quantities

3 Analysis of the Eigenvalues 185

Fig. 14.1 For D ∈ (0, 1.8), the energy difference E(1, 0,D) decreases with the increasing di-

mension D, while increases with the increasing dimension D ∈[1.8, 2.8) and then decreases again

with the increasing dimension D ≥3.2. There exist two singular points around D = 2andD =3.

Note that E(1, 0,D) is symmetrical with respect to point (2.5, 0). The parameter ξ =11/137 is

taken here and also in Figs. 14.2–14.6

Fig. 14.2 Note that the energy difference E(2, 1,D) increases with the increasing dimension

D ∈(0, 0.8), and then decreases with the increasing dimension D ≥1.2

do not depend upon the coordinate in one direction, the Coulomb potential becomes

logarithmic instead of r

−1

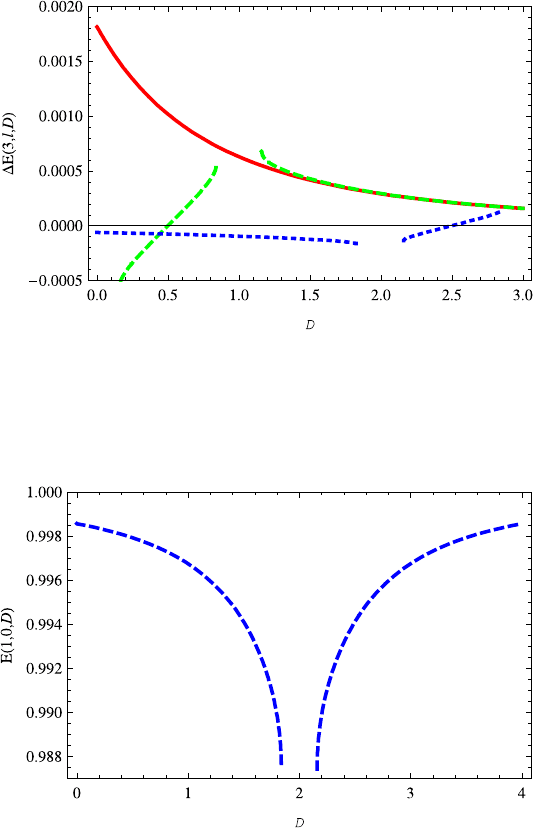
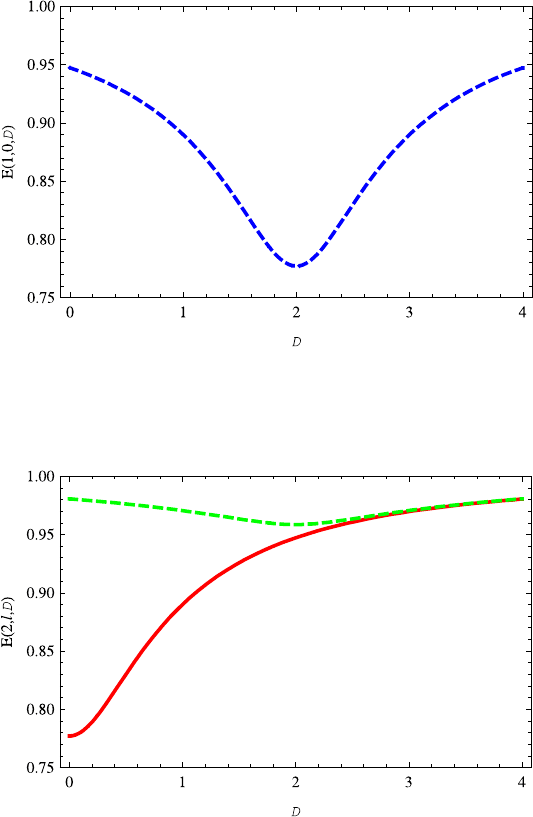
It is shown from Fig. 14.4 that the energy E(1, 0,D)decreases as D increases in

the region (0, 1.8), but increases with it in the region D>2. Figure 14.5 shows the

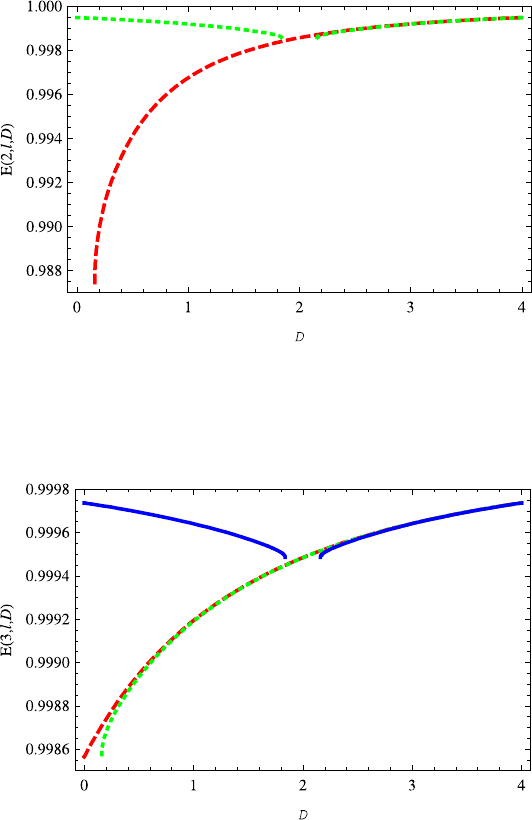
properties of E(2,l,D)(l =1 or 0). The variation of the E(2, 0,D) on D is similar

to energy E(1, 0,D). However, the energy E(2, 1,D) increases monotonically as

186 14 Klein-Gordon Equation with the Coulomb Potential

Fig. 14.3 The variation of energy difference E(3,l,D) on the dimension D. It is noted that

E(3, 2,D) (red solid line) decreases monotonically with the increasing dimension D>0.

The E(3, 1,D) (green dashed line)andE(3, 0,D) (blue dotted line) are very similar to

E(2, 1,D) and E(1, 0,D), respectively

Fig. 14.4 Note that the energy E(1, 0,D) decreases with the increasing dimension D ∈ (0, 1.8),

but increases with the increasing dimension D ≥2.2. It should be stressed that there exists a sin-

gular point around D ∼2. Note that the energy E(1, 0,D)is symmetric with respect to axis D =2

for D ∈(0, 4), so are those energy levels E(n,0,D)

D increases. It is found that the E(2, 1,D)is almost overlapped with the E(2, 0,D)

when D>2. This kind of phenomenon occurs to n = 3 as shown in Fig. 14.6. That

is to say, the energy E(3, 2,D) almost overlaps with the energy E(3, 1,D).This

can be explained well through the series expansion for 1/D as given in Eq. (14.16).

3 Analysis of the Eigenvalues 187

Fig. 14.5 The variation of energy E(2, 0,D) (green dotted line) on the dimension D is very

similar to E(1, 0,D). The energy E(2, 1,D) (red dashed line) increases with the increasing di-

mension D. Specially, it is found for D>2 that the energy E(2, 1,D) almost overlaps E(2, 0,D)

Fig. 14.6 The variation of E(3,l,D) (l = 2, 1, 0) on the dimension D is similar to E(2,l,D)

(l = 1, 0). Note that the energy E(3,2,D) (red dashed line) almost overlaps that of the energy

E(3, 1,D) (green dotted line). When D>2 the energies E(3,l,D) (l = 2, 1, 0) are almost over-

lapped

Before ending this part, we turn to one-dimensional hydrogen atom case due to

its importance in physics. Actually, this problem has been studied by many authors

[188–191]. When D = 1 and Z = 1(ξ

= 1/137), the energy spectrum (14.15)

reduces to the one-dimensional hydrogen atom,

188 14 Klein-Gordon Equation with the Coulomb Potential

E =M

|ξ



1 +

(n −



1 −4ξ

)



−1/2

, (14.23)

which coincides with the result given by Spector and Lee [188], in which Eq. (3)

has a typo on S. The correct expression should be S =1/2 ±1/2(1 −4Z

)

1/2

Here we only take the positive sign for S if considering the behavior of the radial

function at the origin. The quantum number n



used here is n in [188]. The energy

spectrum of the ground state (n =1) can be obtained as

E =M

|ξ



1 +

4ξ

(1 +



1 −4ξ

)



−1/2

. (14.24)

4 Generalization to the Klein-Gordon Equation with a Coulomb

Potential Plus a Scalar Potential

4.1 Introduction

As mentioned above, the Klein-Gordon equation with the Coulomb potential has

been carried out widely in three dimensions. Motivated by our recent work on the

Dirac equation with a Coulomb plus a scalar potential in two dimensions [449] and

in D dimensions [105], we are going to study the exact solutions of the Klein-

Gordon equation with a Coulomb plus a scalar potential in D dimensions. On the

other hand, we attempt to analyze the variations of the eigenvalues E(n,l,D) on

the continuous dimension D.

4.2 Eigenfunctions and Eigenvalues

Considering the motion of a particle in a spherically symmetric Coulomb potential

(r) and the scalar potential V

(r) in D dimensions, we take the time-independent

Klein-Gordon equation as [451]

{−

+[M +V

(r)]

}(r) =[E −V

(r)]

(r), (14.25)

where M and E denote the mass and the energy of the particle, respectively. The

Coulomb potential and the scalar potential are taken as

=−

. (14.26)

It is evident that Eq. (14.25) keeps invariant by interchanging V

(r) →−V

(r) and

E →−E. For simplicity we only discuss the attractive Coulomb potential case

(r) (v>0). The solutions for the repulsive Coulomb potential case V

(r) (v<0)

can be obtained from the former by changing the sign of the energy E. The scalar

potential V

, however, will be discussed in two different cases s>0 and s<0.

4 Generalization to the Klein-Gordon Equation with a Coulomb Potential 189

Following Refs. [20, 112, 242], take the wavefunction as

(r) =r

−(D−1)/2

(r)Y

D−2

...l

(

x). (14.27)

Substitution of this into Eq. (14.25) allows us to obtain the radial Klein-Gordon

equation in D dimensions

(r)



−M

−s

−κ

2(Ev +Ms)



(r) =0. (14.28)

Take a new variable ρ for the bound states:

ρ = 2r



−E

, |E|<M. (14.29)

Equation (14.28) becomes

(ρ)

dρ



−s

−κ



(ρ) +

(ρ) −

(ρ) =0, (14.30)

with

τ =

Ev +Ms

√

−E

. (14.31)

From the behaviors of the radial function at the origin and at inﬁnity, we deﬁne

(ρ) =ρ

λ+

−ρ/2

φ(ρ), λ =



−v

> 0. (14.32)

We only consider the weak Coulomb potential case, i.e., κ

. Otherwise the

solution becomes oscillatory. φ(ρ) satisﬁes the following conﬂuent hypergeometric

equation

φ(ρ)

dρ

+(2λ +1 −ρ)

dφ(ρ)

dρ



τ −λ −



φ(ρ)=0, (14.33)

from which we ﬁnally obtain

(ρ) =N

λ+

−ρ/2



λ −τ +

;2λ +1;ρ



, (14.34)

where N

is the normalization factor to be determined.

We now discuss the eigenvalues. As before, the general quantum condition is

obtained from Eq. (14.34)

τ −λ −



=0, 1, 2,.... (14.35)

Introduce a principal quantum number

n =n



+κ −

+2 =n



+l +1. (14.36)

It is shown from Eqs. (14.31), (14.35) and (14.36) that

Ev +Ms

√

−E

=τ =n −l −



−v

≡β>0. (14.37)

190 14 Klein-Gordon Equation with the Coulomb Potential

The energy E can be solved from Eq. (14.37)

E(n,l,D) =M



−

+β



+β



−

−β

+β





. (14.38)

We now consider some special cases. First, if v = 0, s has to be positive due to

Eq. (14.37)soλ =

√

. Thus, we have a pair of solutions ±E(n,l,D) for the

energy

E(n,l,D) =±M



1 −

(n −l −

√

)



. (14.39)

For a large D,wehave

E(n,l,D) M[1 −2s

−2

+4s

(2n −3)D

−3

−···], (14.40)

which implies that the energy is independent of the l for v =0.

For a small s,wehave

E(n,l,D) M



1 −

2[n +(D −3)/2]



2n +D −3

2l +D −2

−



. (14.41)

Second, if s =0, then λ =

√

−v

.DuetoEq.(14.37), the energy E has the

same sign as v when κ

. For the attractive Coulomb potential (v>0), we have

the positive energy

E(n,l,D) =M



1 +

(n −l −

√

−v

)



−

. (14.42)

It coincides with the conclusion from the Sturm-Liouville theorem for a weak at-

tractive potential [184]. For a large D, we have the similar result to Eq. (14.40)(s is

replaced by v).

For a small v,wehave

E(n,l,D) M

|v|



1 −

2[n +(D −3)/2]

−

2[n +(D −3)/2]



2n +D −3

2l +D −2

−



. (14.43)

Third, if v =s, from Eq. (14.37) both v and s have to be positive, λ =|κ|, and

the positive β is given by

β =n −l −

+|κ|=



n +

D−3

, when κ ≥0,

n −2l +

1−D

, when κ<0.

(14.44)

When κ ≥0, we obtain from Eq. (14.37)

E(n,l,D) =M



1 −

+(n +

D−3

)



. (14.45)

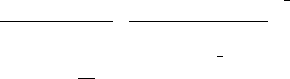
4 Generalization to the Klein-Gordon Equation with a Coulomb Potential 191

The energy is independent of the l. However, when κ<0, the energy depends

upon l.

We now calculate the normalization factor N

from the normalization condition



∞

(ρ)

dr =1 (14.46)

−E

)

1/4

β(2λ +1)



2β(n



+2λ +1)



!(2n



+2λ +1)



λ =



l −1 +



−v



(14.47)

4.3 Analysis of the Energy Levels

We now analyze the variation of energy E(n,l,D) on the continuous dimension D.

It is shown from Eqs. (14.32) and (14.37) that the energy E(n,l,D) given in

Eq. (14.39) is closely related with the following two conditions,

+κ

,Ev+Ms > 0, (14.48)

from which we can determine whether the energy is positive or negative. Recall

that we only consider the case with positive v. For the negative v case, the energy

E(n,l,D) changes its sign. For simplicity we take M =1.

First, we consider the case s>0. We discuss the energy E(n,l,D) in two cases

with s>vand s<v. When s>v, due to Eq. (14.48) the bound states with 0 <E<

M is an acceptable solution. We take v = 0.2 and s = 0.3 for the weak attractive

Coulomb potential. On the other hand, the sign “+” is taken for the second term

of Eq. (14.38). If we take the sign “−”, the variations are absolutely different from

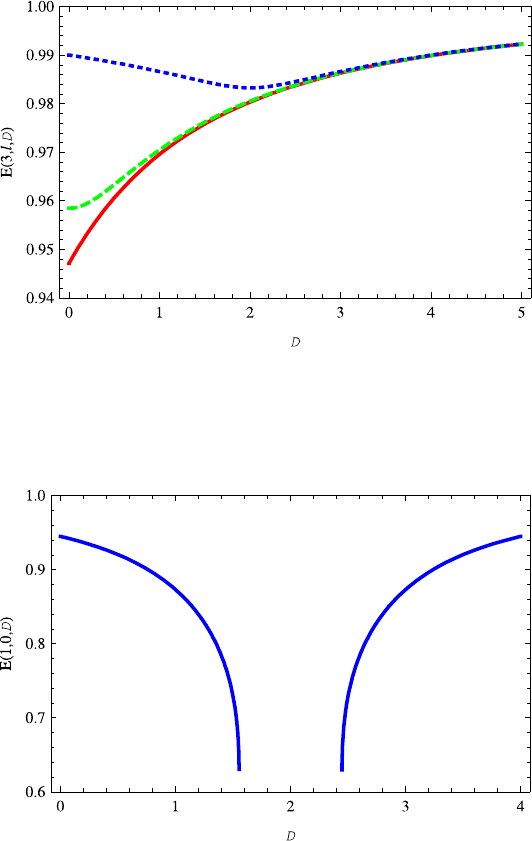
each other. It is found from Figs. 14.7, 14.8, 14.9 that the energy E(n,0,D) ﬁrst

decreases for D ∈ (0, 2) and then increases with the dimension D ≥ 2, while the

energy E(n,l,D) (l =0) is almost independent of the angular momentum quantum

number l. Also, the energy E(n,l,D) are almost overlapped for a large D.Itis

shown that the energy E(n,0,D)is symmetric with respect to D =2forD ∈(0,

4).

When s<v,wetakev =0.3 and s =0.2. Note that there is no bound state for l =0

and near D ∼ 2 since λ<0. The corresponding variations of energy E(n,l,D)

on the dimensions D are illustrated in Figs. 14.10, 14.11, 14.12. It is shown from

Fig. 14.10 that the energy E(1, 0,D) decreases with the increasing dimension D ∈

(0, 1.4], but increases with the increasing dimension D ≥ 2.4. There is no bound

state for D ∈[1.6, 2.4]. It is shown from Figs. 14.11 and 14.12 that variation of

the energy E(n,0,D) (n = 2, 3) on the dimension D is very similar to E(1, 0,D).

For the same reason (λ<0), there is no bound state when l =1 and D ∈

(0, 0.4].

The energy E(n,1,D) (n =2, 3) increases with the dimension D ≥ 0.4. It is found

that the energy E(n,l,D) is almost independent of the quantum number l for a

large D. It should be pointed out that the variant range of the dimension D in which

192 14 Klein-Gordon Equation with the Coulomb Potential

Fig. 14.7 The energy E(1, 0,D) decreases with the dimension D ∈ (0, 2), but increases with

the increasing dimension D ≥ 2. The parameters v =0.2ands = 0.3 are taken here and also in

Figs. 14.8 and 14.9. Note that the energy E(1, 0,D) is symmetric with respect to axis D =2

Fig. 14.8 The variation of energy E(2, 0,D)(green dashed line) on the dimension D is very simi-

lar to E(1, 0,D). The energy E(2,1,D)(red solid line) increases with the increasing dimension D.

For D>2 the energy E(2, 1,D) almost overlaps E(2, 0,D)

the bound state is not admissible is closely related with the values of the potential

parameters v and s.

Second, we consider the case v>0 and s<0. If −s =|s|≥v, there is no bound

state due to Eq. (14.37). However, if −s =|s| <v, the variation of the energy

E(n,l,D) on the dimension D is similar to that of the case 0 <s<v as shown

above (see Figs. 14.10, 14.11, 14.12).

4 Generalization to the Klein-Gordon Equation with a Coulomb Potential 193

Fig. 14.9 The variations of the E(3,l,D) (l = 2, 1, 0) on the dimension D are similar to

E(2,l,D)(l =1, 0). The energy E(3, 2,D) (red solid line) almost overlaps the energy E(3, 1,D)

(green dashed line) for a large D.ForD>2, the energies E(3,l,D) (l =2, 1, 0) are almost over-

lapped. The red solid, green dashed and blue dotted lines correspond to l =2, 1, 0, respectively

Fig. 14.10 The energy E(1, 0,D) decreases with the increasing dimension D ∈ (0, 1.6],butin-

creases with the increasing dimension D ≥ 2.4. There are no bound states for D ∈[1.6, 2.4].The

parameters v =0.3ands =0.2 are taken here and also in Figs. 14.11 and 14.12

We now consider some special cases below. First, for the special case s =0 and

v = 0, namely, the Klein-Gordon equation with the Coulomb potential has been

carried out in our recent work [100]. Second, for the special case v = 0buts =0,

it is shown from Eq. (14.48) that there are bound states for s>0, say s = 0.2.

The variations of energy levels on the dimension D showninFigs.14.13, 14.14,