Dong S.-H. Wave Equations in Higher Dimensions

Подождите немного. Документ загружается.

194 14 Klein-Gordon Equation with the Coulomb Potential

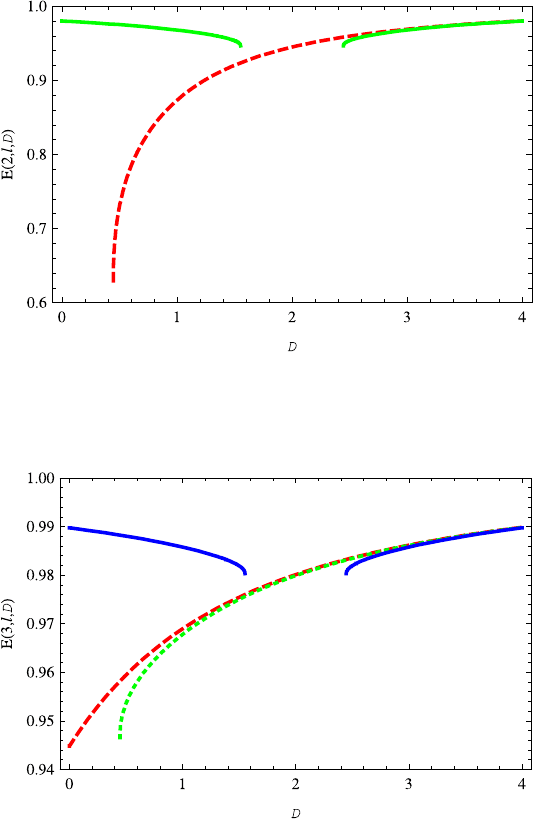
Fig. 14.11 The variation of the energy E(2, 0,D) (green solid line) on the dimension D is

very similar to E(1,0,D). The energy E(2, 1,D) (red dashed line) increases with the dimension

D ≥0.4. The energy E(2, 1,D)almost overlaps E(2, 0,D)for D ≥2.6

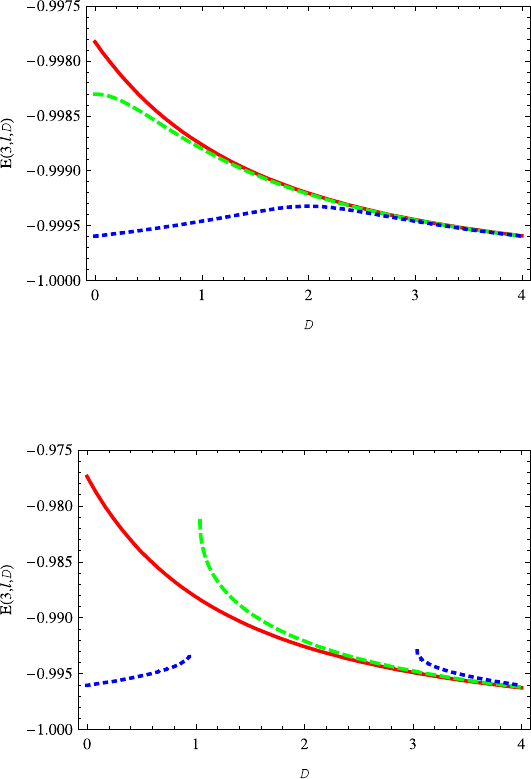
Fig. 14.12 The variation of the E(3,l,D)(l =2, 1, 0) on the dimension D is similar to E(2,l,D)

(l =1, 0). For D ≥2.6 the energies E(3,l,D) (l =2, 1, 0) are almost overlapped. The red dashed,

green dotted and blue solid lines correspond to l =2, 1, 0, respectively

14.15 are similar to those of the case s = 0.3 and v = 0.2inFigs.14.7, 14.8,

14.9. Third, for the special case v = s, there are bound states for the positive

s = v>0. The corresponding variations of energy E(n,l,D) on the dimension

D are shown in Figs. 14.16, 14.17, 14.18. Basically, their variations are similar

to those of case v = 0.2 and s = 0.3 as shown in Figs. 14.7, 14.8, 14.9.How-

ever, the energies E(n,l,D) (l = 0) are completely independent of the quantum

4 Generalization to the Klein-Gordon Equation with a Coulomb Potential 195

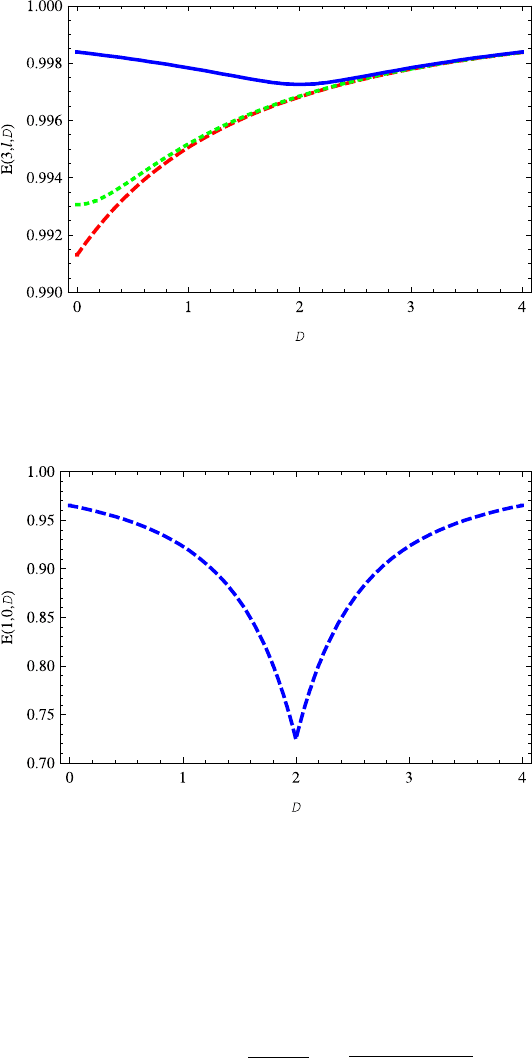
Fig. 14.13 The energy E(1,0,D) decreases with the increasing dimension D ∈ (0, 2),butin-

creases with the increasing dimension D ≥ 2. The parameters v = 0ands = 0.2aretakenand

also in Fig. 14.14. Note that its variation is very similar to that illustrated in Fig. 14.7 except for a

different amplitude

Fig. 14.14 The variation of energy E(2, 0,D)(green solid line) on the dimension D is very simi-

lar to E(1, 0,D). The energy E(2, 1,D)(red dashed line) increases with dimension D. The energy

E(2, 1,D) almost overlaps E(2, 0,D) for D>2.6

number l since κ>0forl = 0. This can be explained well from Eq. (14.45). For

D>2.6 the energies E(3,l,D) (l = 2, 1, 0) are almost overlapped. However, the

energy E(n,0,D)is closely related with the angular momentum quantum number l

asshownbyFigs.14.16, 14.17, 14.18.

196 14 Klein-Gordon Equation with the Coulomb Potential

Fig. 14.15 The variations of the E(3,l,D) (l = 2, 1, 0) on the dimension D are similar to

E(2,l,D) (l =1, 0). The energy E(3, 2,D) (red dashed line) almost overlaps energy E(3, 1,D)

(green dotted line). For D>2.6, the energies E(3,l,D) (l =2, 1, 0) are almost overlapped

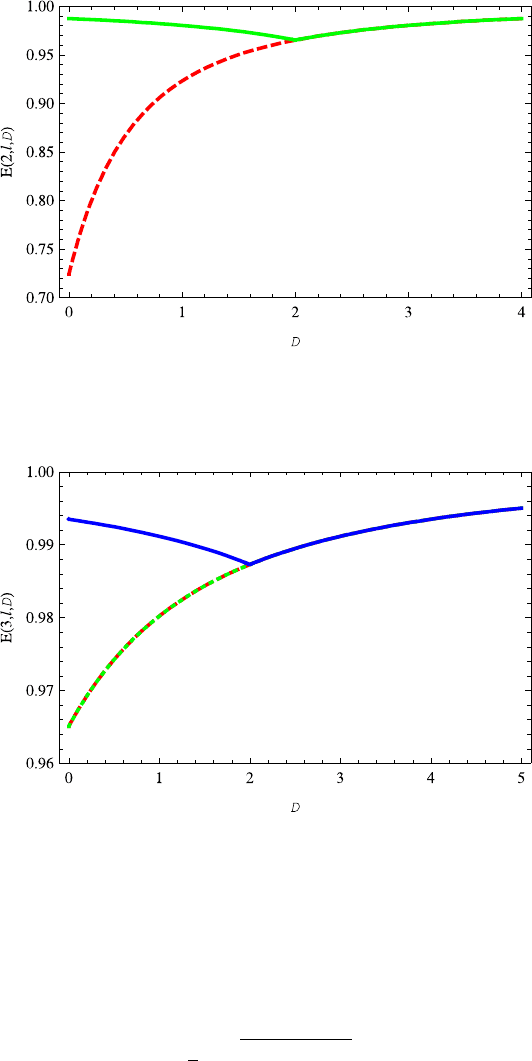
Fig. 14.16 The energy E(1,0,D) decreases with the increasing dimension D ∈ (0, 2),butin-

creases with the increasing dimension D ≥ 2. Note that it is symmetric with respect to the axis

D =2. The parameters v =s =0.2 are chosen here and also in Figs. 14.17 and 14.18

We now brieﬂy study the variations of energy levels on the potential strengths

v and s for D = 3. The constraints on the potential parameters v and s are closely

related to the λ given in Eq. (14.32). That is, v

≤ κ

+ s

= (l + 1)

+ s

but

≥ v

−κ

= v

−(l + 1/2)

. In general, there is no constraint on the potential

strength s for the small v (weak potential strength). However, there is a constraint

on the potential strength v, i.e., |v|≤

√



(l +1/2)

. These features

4 Generalization to the Klein-Gordon Equation with a Coulomb Potential 197

Fig. 14.17 The variation of the energy E(2, 0,D) (green solid line) on the dimension D is

very similar to E(1, 0,D). The energy E(2, 1,D) increases with the dimension D. The energy

E(2, 1,D) (red dashed line) completely overlaps E(2, 0,D) for D ≥2

Fig. 14.18 The variation of the E(3,0,D) (blue solid line) on the dimension D is similar to

E(n,0,D) (n = 2, 1). The energy E(3, 2,D) (red dashed line) overlaps the E(3, 1,D) (green

dotted line) completely. For D ≥2 the energies E(3,l,D) (l =2, 1, 0) are completely overlapped

are displayed in Figs. 14.19 and 14.20. It is interesting to notice that the energy

E(n,l,v) decreases with the parameter v ≤l +1 for a given l.

Let us turn to one-dimensional case. When D =1, the energy E(n,l,D) reduces

to a similar expression to Eq. (14.39), but with a different β

β =n −



1/4 +s

−v

. (14.49)

198 14 Klein-Gordon Equation with the Coulomb Potential

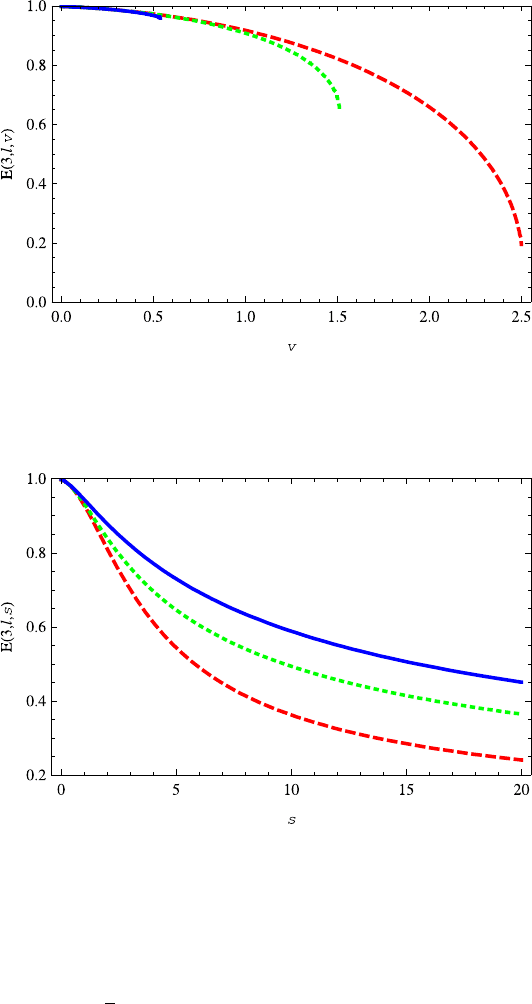
Fig. 14.19 The variation of the energy levels E(3,l,v)(l = 0, 1, 2) on the parameter v. The energy

decreases with the parameter v.Thered dashed, green dotted and blue solid lines correspond to

l =2, 1, 0, respectively. The parameters D =3ands =0.2aretaken

Fig. 14.20 The variation of the energy levels E(3,l,s) on the parameter s. The energy decreases

with the v.Thered dashed, green dotted and blue solid lines correspond to the l =2, 1, 0, respec-

tively. The parameters D =3andv =0.2aretaken

The energy E(n,l,D) is determined by two conditions

,Ev+Ms > 0. (14.50)

The discussion is similar to that of the general case as studied above. We do not

mention them for simplicity.

4 Generalization to the Klein-Gordon Equation with a Coulomb Potential 199

Fig. 14.21 The plot of energy levels E(2,l,D) as a function of dimension D for energy (14.38)

with sign “−”. The red solid and green dashed lines correspond to l = 1, 0, respectively. The

v =0.3ands =0.2aretaken

Fig. 14.22 The plot of energy levels E(3,l,D)as a function of dimension D.Thered solid, green

dashed and blue dotted lines correspond to l =2, 1, 0, respectively. Same parameters are taken as

those in Fig. 14.21

Before ending this section, let us mention the case of Eq. (14.38) with sign “−”.

To show this, we are going to illustrate it in Figs. 14.21, 14.22, 14.23, 14.24 by

choosing suitable parameters. It is found that its variation is absolutely different

from the case with “+” sign. Their absolute values of energy spectrum are same but

with different signs.

200 14 Klein-Gordon Equation with the Coulomb Potential

Fig. 14.23 The plot of energy levels E(3,l,D)as a function of dimension D.Thered solid, green

dashed and blue dotted lines correspond to l =2, 1, 0, respectively. The parameters v =0.2and

s =0.3aretaken

Fig. 14.24 The plot of energy levels E(3,l,D)as a function of dimension D.Thered solid, green

dashed and blue dotted lines correspond to l = 2, 1, 0, respectively. Here the parameters v = 0.6

and s =0.3 are chosen

5 Comparison Theorem

Finally, we present the comparison theorem for Klein-Gordon equation in arbi-

trary dimensions D. In non-relativistic quantum mechanics, this theorem is an im-

mediate consequence of the variational characterization of the bound state spec-

trum as shown in Chap. 9. In the Klein-Gordon equation case, recently Hall and

Aliyu have dealt with this problem [103]. It is found that if ψ

and ψ

are node-

free ground states corresponding to positive energies E

≥ 0 and E

≥ 0 and

6 Concluding Remarks 201

(r) ≤ V

(r) ≤ 0, then one has E

≤ E

. On the other hand, if V(r,a) depends

on a parameter a ∈ (a

), and E(a) is any positive eigenvalue, then one has

∂V/∂a ≥ 0 ⇒ E



(a) ≥ 0 and ∂V/∂a ≤ 0 ⇒E



(a) ≤ 0. This can be easily proved

by using Eq. (14.3). For ordered central potentials V

(r) ≤ V

(r), suppose that the

respective ground states {ψ

(r), ψ

(r)} in Eq. (14.3) are node-free and write the

corresponding energy levels as {E

}. The two eigenfunctions are written by

−ψ



(r) +

(r) ={[E

−V

(r)]

−M

}ψ

(r), (14.51)

−ψ



(r) +

(r) ={[E

−V

(r)]

−M

}ψ

(r), (14.52)

with C =(2l +D −1)(2l +D −3)/4.

With these two equations we calculate the difference between Eq. (14.51)mul-

tiplied by ψ

(r) and Eq. (14.52) multiplied by ψ

(r) and integrating it over the

argument r ∈[0, ∞) to give the following equation

−E

)



∞

W(r)ψ

(r)ψ

(r)dr



∞

(r) −V

(r)]W(r)ψ

(r)ψ

(r)dr, (14.53)

with

W(r)=E

−V

(r) −V

(r). (14.54)

Thus, for positive energy levels E

belonging to node-free ground states ψ

(r)

and ψ

(r),wehaveE

≤E

if V

(r) ≤V

(r) ≤0.

6 Concluding Remarks

In this Chapter we have studied the D-dimensional Klein-Gordon equation with a

Coulomb potential. The exact solutions have been analytically obtained. It is worth

pointing out that when the Coulomb potential is not very strong, an attractive poten-

tial leads to the bound states with positive energies, and a repulsive potential leads

to those with negative energies.

The variation of the energy difference E(n,l,D)on the dimension D has been

analyzed in detail. In general, there are three kinds of variations. First, the energy

difference E(n, 0,D) ﬁrst decreases, then increases, and ﬁnally decreases as the

dimension D increases. In other words, we have found that E(n,l,D) is sym-

metric with respect to the point (2.5, 0). Second, it is seen that E(n, 1,D) ﬁrst

increases and then decreases as D increases. There exists a singular point around

D = 1. Third, we have noticed that E(n, 2,D) decreases monotonically as D in-

creases. As far as the energy E(n,l,D) is concerned, the following properties are

displayed. First, when l = 0 there is no bound state around D =2, i.e., E(n,0,D)

202 14 Klein-Gordon Equation with the Coulomb Potential

ﬁrst decreases and then increases with D>2.4. More precisely, E(n,l,D) is sym-

metric with respect to axis D =2. The energy E(n,l,D) with l>0 is almost inde-

pendent of the quantum number l for a large D.

As a generalization, we have also studied the D-dimensional Klein-Gordon equa-

tion with a Coulomb plus a scalar potential. The eigenfunctions have been gotten

analytically. We have investigated the variation of the energy E(n,l,D) on the di-

mension D in some detail. We have observed following typical properties. First, the

positive energy E(n,0,D) ﬁrst decreases with the dimension D and then increases

with it. We have found that E(n,0,D) is symmetric with respect to axis D = 2.

When v<s, there is no singular point at D = 2, while there exists one singular

point when v>s. Second, the positive E(n,l,D) (l = 0) increases with the di-

mension D. Third, the variations of the negative E(n,0,D) and E(n,l,D) (l = 0)

on the dimension D are completely opposite to those of the positive cases. Fourth,

the energy E(n,l,D) is almost independent of the angular momentum quantum

number l for a large D and the E(n,l,D) (l = 0) are almost overlapped. Also, the

variations of the energy levels E(n,l,v) and E(n,l,s) on the parameters v and s

have been studied. It is found that the energy levels decrease with those parameters.

Interestingly, we have found that the energy E(n,l,v) decreases with the parameter

v ≤l +

1 for a given l.

Finally, the comparison theorem has been established by the traditional method.

It is found that for positive energy levels E

belonging to node-free ground

states ψ

(r) and ψ

(r) we have E

≤E

if V

(r) ≤V

(r) ≤0.

Chapter 15

The Levinson Theorem for Dirac Equation

1 Introduction

The Levinson theorem [109] is an important theorem in the quantum scattering the-

ory, which sets up the relation between the number of bound states and the phase

shift at zero momentum. It has been generalized and applied to different ﬁelds in

modern physics [184, 247–296]. With the interest of higher-dimensional ﬁeld the-

ory, the Levinson theorem for the Schrödinger equation in arbitrary D dimensions

was studied [112].

As mentioned in Part I, we have generalized the Dirac equation with a spherically

symmetric potential to arbitrary (D +1) dimensions and constructed the eigenfunc-

tions of the total angular momentum. We have also derived the radial equations [91].

It is found that the total (or orbital, spinor) angular momentum in D-dimensional

space can be described by an irreducible representation of the SO(D) group denoted

by the highest weight, instead of only one parameter j (or l, s) in three-dimensional

space.

In this Chapter we shall uniformly study the Levinson theorem for the Dirac

equation in (D + 1) dimensions by the Sturm-Liouville theorem. In Sect. 2 we

study the generalized Sturm-Liouville theorem. The number of bound states will

be calculated in Sect. 3. In Sect. 4 the Levinson theorem is established by proving

the number of bound states to be equal to the sum of the phase shifts of the scat-

tering states at E =±M with the given angular momentum. The critical cases are

also analyzed there. Some discussions are given in Sect. 5. Due to the connection

between the Levinson theorem and the Friedel theorem, we shall present in Sect. 6

the Friedel theorem in arbitrary dimensions D. We shall outline the comparison the-

orem for radial Dirac equations in arbitrary dimensions D in Sect. 7. Finally, we

conclude this Chapter in Sect. 8.

S.-H. Dong, Wave Equations in Higher Dimensions,

203