Dong S.-H. Wave Equations in Higher Dimensions
Подождите немного. Документ загружается.

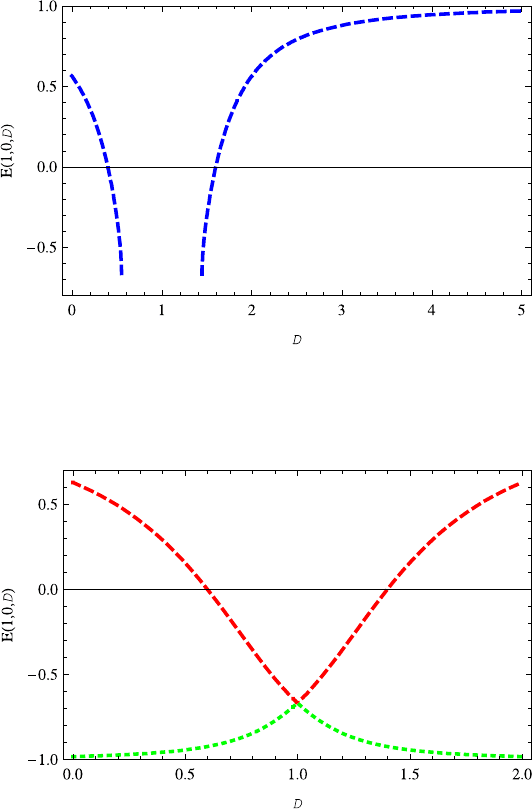
174 13 Dirac Equation with the Coulomb Potential
Fig. 13.13 The energy E(1, 0,D) decreases with the increasing dimension D ∈ (0, 0.55],but
increases with the increasing dimension D ≥1.45. There are no bound states for D ∈(0.55, 1.45).
The parameters v =0.3ands =0.2 are taken here and also in Figs. 13.15 and 13.16
Fig. 13.14 The plot of energy spectra E(1,0,D) as a function of dimension D. Two signs “±”
are considered. Note that their variations are absolutely different from each other
most independent of the quantum number l for a large D. It should be addressed
that the variation range of dimension D without permitting bound state depends on
the values of the potential parameters v and s. On the contrary, if we choose the sign
“−” for the second term of Eq. (13.57), the variation will be opposite to that of the
sign “+” as illustrated in Fig. 13.14.
Second, we consider the case v>0 and s<0. If −s =|s|≥v, there is no bound
state according to Eq. (13.67). However, if −s =|s| <v, the variations of ener-
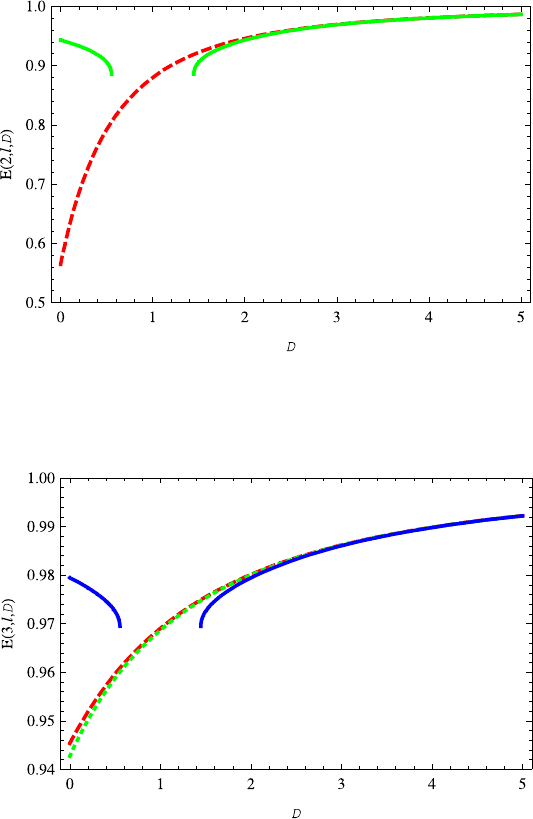
4 Generalization to the Dirac Equation 175
Fig. 13.15 The variation of energy E(2, 0,D) (green solid line) on the dimension D is similar
to E(1, 0,D). The energy E(2, 1,D) (red dashed line) increases with dimension D. The energy
E(2, 1,D) almost overlaps E(2, 0,D) for D ≥ 2
Fig. 13.16 The variations of energy levels E(3,l,D)on the dimension D are similar to E(2,l,D)
(l =1, 0). For D ≥ 2 the energies E(3,l,D) (l = 2, 1, 0) are almost overlapped. The red dashed,
green dotted and blue solid lines correspond to the l =2, 1, 0, respectively
gies E(n,l,D) are similar to those of the case 0 <s<v as studied above (see
Figs. 13.13, 13.14, 13.15, 13.16). We do not show them for simplicity.
We now consider some special cases. First, for special case s = 0 and v = 0,
i.e., the Dirac equation with the Coulomb potential has been investigated in our re-
cent work [104, 450]. Second, for special case v = 0, but s = 0, it is shown from
Eq. (13.67) that there are bound states for s>0, say s =0.2. The variations of the
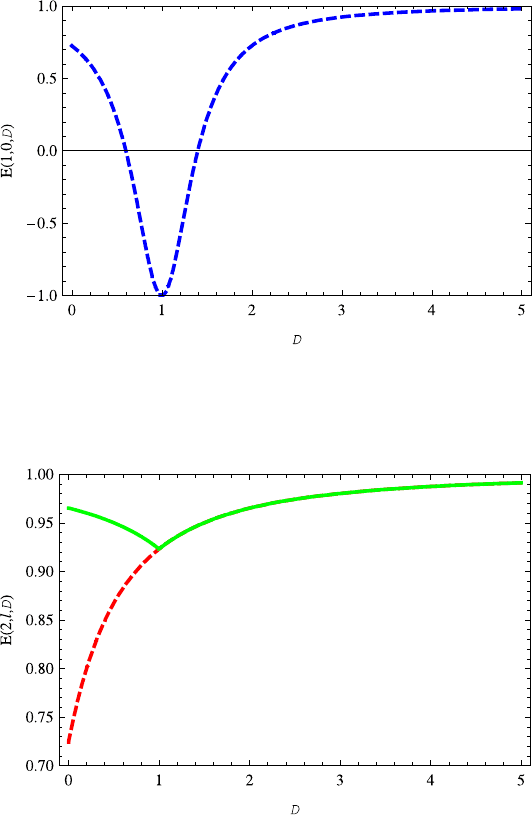
176 13 Dirac Equation with the Coulomb Potential
Fig. 13.17 The energy E(1,0,D) decreases with the increasing dimension D ∈ (0, 1),butin-
creases with the increasing dimension D ≥1. The parameters v =s = 0.2 are taken here and also
in Figs. 13.18 and 13.19
Fig. 13.18 The variation of energy E(2, 0,D) (green solid line) on the dimension D is similar
to E(1, 0,D). The energy E(2,1,D) (red dashed) increases with the dimension D. The energy
E(2, 1,D) completely overlaps E(2, 0,D) for D ≥ 1
energies on the dimension D are similar to those of the case s = 0.3 and v = 0.2
given in Figs. 13.10, 13.11, 13.12. Likewise, we do not show them here. Third,
for special case v = s, there are bound states for positive s = v>0. The corre-
sponding variations of the energies E(n,l,D) on the dimension D are displayed
in Figs. 13.17, 13.18, 13.19. Basically, the variations of the energies on the dimen-
sion D are similar to those of the case v = 0.2 and s = 0.3 given in Figs. 13.10,

5 Concluding Remarks 177
Fig. 13.19 The variation of energy E(3, 0,D) on the dimension D is similar to E(n,0,D)
(n = 2, 1). The energy E(3, 2,D) overlaps E(3, 1,D) completely. For D ≥ 1 the energies
E(3,l,D) (l = 2, 1, 0) are completely overlapped. The red dashed, green dotted and blue solid
lines correspond to l =2, 1, 0, respectively
13.11, 13.12. However, the energies E(n,l,D) (l = 0) are completely independent
of quantum number l. This can be explained well from Eq. (13.64)forK>0. For
D ≥ 2 the energies E(3,l,D) (l = 2, 1, 0) are overlapped. However, the energy
E(n,0,D) is closely related to the quantum number l as shown in Figs. 13.17,
13.18, 13.19. Also, this can be explained well by Eq. (13.64)forK<0. It should
be pointed out that there exists a singular solution E =−M =−1forD =1 and
l =0.
We now briefly study the variations of energies on the potential strengths v
and s for a given D = 3 even though such a study which is not less important in
physics. The constraints on the potential parameters v and s are closely related
to the λ defined in Eq. (13.46). That is to say, v
2
≤ K
2
+ s
2
= (l +1)
2
+ s
2
but
s
2
≥ v
2
− K
2
= v
2
− (l + 1)
2
. Generally speaking, there is no constraint on the
potential strength s for a small v (weak potential strength). However, there is a con-
straint on the potential strength v, i.e., |v|≤
√
K
2
+s
2
=
(l +1)
2
+s
2
. These
features are shown in Figs. 13.20 and 13.21. The detailed study for the constraint on
the potential strength v can be found in Ref. [450].
5 Concluding Remarks
In this Chapter we have studied the (D + 1)-dimensional Dirac equation with the
1/r type potential through the confluent hypergeometric equation approach. This
is different from the method used in our previous work [91]. The eigenfunctions
are analytically obtained. The eigenvalues and the fine structure energy have also
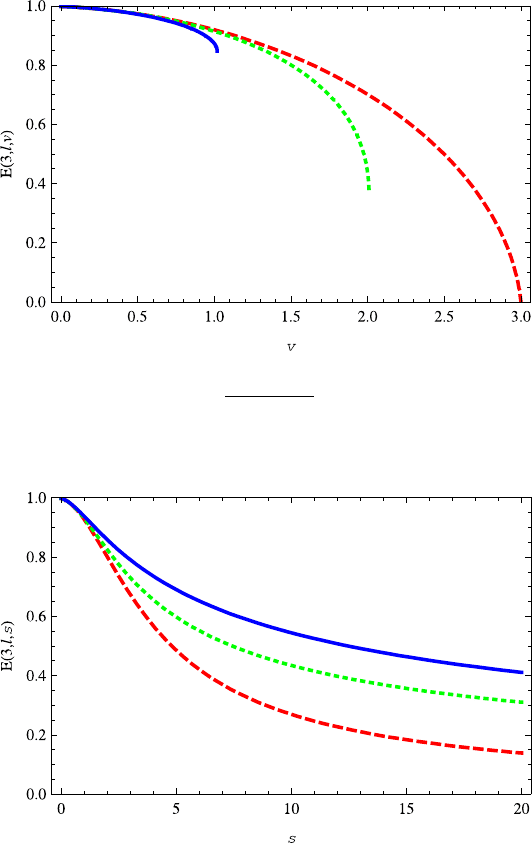
178 13 Dirac Equation with the Coulomb Potential
Fig. 13.20 The plot of energy levels E(3,l,v) (l = 0, 1, 2) as a function of parameter v.They
decrease with the parameter v.Thev ≤
(l +1)
2
+s
2
for D = 3. The red dashed, green dotted
and blue solid lines correspond to l = 2, 1, 0, respectively. The parameters D = 3ands =0.2are
taken
Fig. 13.21 The plot of energy levels E(3,l,s) (l = 2, 1, 0) as a function of parameter s.The
energy decreases with s.Thered dashed, green dotted and blue solid lines correspond to l =2, 1, 0,
respectively. The parameters D =3andv =0.2 are chosen
been studied. The present work has paid more attention to the variations of energy
differences E(n,l,D) and the energy levels E(n,l,D) on the continuous dimen-
sion D. The variations of energy differences E(n,l,D) on the dimension D have
been analyzed. Generally speaking, there exist three different kinds of variations.
First, note that the energy difference E(n, 0,D) first decreases, then increases,

5 Concluding Remarks 179
and finally decreases as the dimension D increases. That is, the E(1, 0,D)is sym-
metric with respect to the point (1.5, 0). Second, we have found that E(n, 1,D)
decreases with the D, but there are no bound states when D<0.1. Third, notice
that E(n,l,D) decreases monotonically with the dimension D.
For the energy E(n,l,D), we have following properties. For the energy levels
E(n,0,D), there exists a singular point at D =1. That is, the E(n,0,D)is symmet-
ric with respect to axis D =1forD ∈(0, 2). The energies E(n,0,D)first decrease
with the dimension D and then increase with it. The energies E(n,l,D) (l>0) are
almost independent of quantum number l for a large D.
The variations of energy levels E(n,l,ξ) on potential strength ξ have also been
analyzed. For a given dimension D = 3, the energy E(n,l,ξ) decreases with the
potential parameter ξ ≤l +1.
As a generalization, we have studied the Dirac equation with a Coulomb po-
tential plus a scalar potential. The eigenvalues and some special cases have been
carried out. We have elucidated the variations of energies E(n,l,D) on the di-
mension D and found following typical properties. First, the energies E(n,
0,D)
first decrease with the dimension D and then increase with it. The energy levels
E(n,l,D) (l =0) increase with the dimension D. Second, the energies E(n,l,D)
are almost independent of quantum number l and the E(n,l,D) (l =0) are almost
overlapped for a large D. Third, the energies E(n,0,D) are symmetric with the
respect to D = 1forD ∈ (0, 2). This is different from the case without the scalar
potential. The variations of energies on potential parameters v and s are also stud-
ied for D = 3. We have found that the constraints on the potential parameters v
and s are closely related to the parameter λ, i.e., v
2
≤K
2
+s
2
=(l + 1)
2
+s
2
but
s
2
≥ v
2
− K
2
= v
2
− (l + 1)
2
. Generally speaking, there is no constraint on the
potential strength s for a small v. However, there is a constraint on the potential
strength v, i.e., |v|≤
√
K
2
+s
2
=
(l +1)
2
+s
2
. We have found that the energy
levels E(n,l,v) and E(n,l,s) decrease with the parameters v and s. In particular,
it is interesting to observe that the E(n,l,v) decreases with parameter v ≤l +1for
agivenl.

Chapter 14
Klein-Gordon Equation with the Coulomb
Potential
1 Introduction
The exact solutions of non-relativistic and relativistic equations with the Coulomb
potential have become an important subject in quantum mechanics. During the past
several decades, the Klein-Gordon equation with the Coulomb potential has been
studied in three dimensions such as the operator analysis [185], in an intense laser
field [186], in two dimensions [187] and in one dimension [188–191]. With the in-
terest of the higher-dimensional field theory, the Schrödinger equation and the Dirac
equation with a Coulomb potential have been studied in (D +1) dimensions. The
Klein-Gordon equation with a Coulomb potential in (D + 1) dimensions has been
discussed by the different approaches such as the large-N expansion approximate
method [93] and the associated Laguerre equation approach [64], which paid more
attention to the hydrogen atom case than the relativistic pi-mesonic atom one. The
purposes of this Chapter are two-fold. The first one is to re-study this problem fol-
lowing the confluent hypergeometric equation approach. The another one, which is
the main purpose of this Chapter, is to analyze the variations of the eigenvalues on
the dimension D [64, 87].
This Chapter is organized as follows. Section 2 is devoted to the derivation of
the eigenfunctions and eigenvalues. The properties of the eigenvalues are analyzed
in Sect. 3. The Klein-Gordon equation with the Coulomb potential plus a scalar
potential will be considered in Sect. 4. The comparison theorem is studied in Sect. 5.
Some conclusions are given in Sect. 6.
2 Eigenfunctions and Eigenvalues
For simplicity the atomic units =c = 1 are employed if not explicitly stated other-
wise. Considering the motion of a particle in a spherically symmetric potential V(r)
in D dimensions, the time-independent Klein-Gordon equation is taken as
(−
2
+M
2
)(r) =[E −V(r)]
2
(r), (14.1)
where M and E denote the mass and the energy of the particle, respectively.
S.-H. Dong, Wave Equations in Higher Dimensions,
DOI 10.1007/978-94-007-1917-0_14, © Springer Science+Business Media B.V. 2011
181

182 14 Klein-Gordon Equation with the Coulomb Potential
As illustrated in previous Chapters, take the wavefunction of the form
(r) =r
−(D−1)/2
R
l
(r)Y
l
l
D−2
...l
1
(
ˆ
x). (14.2)
Substitution of this into Eq. (14.1) yields
d
2
dr
2
−
κ
2
−1/4
r
2
R
l
(r) =−{[E −V(r)]
2
−M
2
}R
l
(r), (14.3)
where κ ≡l −1 +D/2.
For the present work, the symmetric potential V(r)is taken as the Coulomb-type
one
V(r)=−
ξ
r
,ξ=Zα. (14.4)
We will discuss the weak potential, say |ξ |< 1/2. The radial equation (14.3) thus
becomes
d
2
R
l
(r)
dr
2
+
ξ
2
−κ
2
+1/4
r
2
R
l
(r) +
2Eξ
r
R
l
(r) +(E
2
−M
2
)R
l
(r) =0. (14.5)
It is convenient to take a new variable ρ for the bound states:
ρ = 2r
M
2
−E
2
, |E|<M. (14.6)
As a result, Eq. (14.5) is changed to
d
2
R
l
(ρ)
dρ
2
+
1
ρ
2
ξ
2
−κ
2
+
1
4
R
l
(ρ) +
τ
ρ
R
l
(ρ) −
1
4
R
l
(ρ) =0, (14.7)
with
τ =
Eξ
√
M
2
−E
2
. (14.8)
From the behaviors of the radial function at the origin and at infinity, we define
R
l
(ρ) =ρ
λ+1/2
e
−ρ/2
φ(ρ), λ =
κ
2
−ξ
2
> 0, (14.9)
where we assume κ
2
>ξ
2
. φ(ρ) satisfies the following confluent hypergeometric
equation
ρ
d
2
φ(ρ)
dρ
2
+(2λ +1 −ρ)
dφ(ρ)
dρ
+(τ −λ −1/2)φ(ρ) =0. (14.10)
Finally, the radial function can be expressed as
R
l
(ρ) =N
l
ρ
λ+1/2
e
−ρ/2
1
F
1
(λ −τ +1/2;2λ +1;ρ), (14.11)
where N
l
is the normalization factor to be determined.
We now discuss the eigenvalues. From the consideration of the finiteness of the
solutions at infinity, the general quantum condition is obtained from Eq. (14.11)
τ −λ −1/2 =n
=0, 1, 2,.... (14.12)

3 Analysis of the Eigenvalues 183
Introduce a principal quantum number
n =n
+κ −D/2 +2 =n
+l +1. (14.13)
BasedonEqs.(14.8) and (14.12), we obtain
Eξ
√
M
2
−E
2
=τ =n −l −1/2 +
κ
2
−ξ
2
> 0. (14.14)
Therefore, we can obtain E with the same sign as ξ
E(n,l,D) =M
ξ
|ξ|
1 +
ξ
2
(n −l −1/2 +
κ
2
−ξ
2
)
2
−1/2
, (14.15)
which essentially coincides with that of Ref. [87] except that the factor ξ/|ξ | was
not considered there.
For a large D,wehave
E(n,D) =M
ξ
|ξ|
[1 −2ξ
2
D
−2
+4ξ
2
(2n −3)D
−3
−···]. (14.16)
For a small ξ ,wehave
E(n,l,D) =M
ξ
|ξ|
1 −
ξ
2
2[n +(D −3)/2]
2
+
ξ
4
(D +6l −4n)
4(2l −2 +D)[n +(D −3)/2]
4
, (14.17)
where the first term on the right hand side is the rest energy M (c =1), the second
one is from the solutions of the Schrödinger equation with this potential, and the
third one is the fine structure energy, which removes the degeneracy between the
states with the same n.
We now calculate the normalization factor N
l
from the normalization condition
∞
0
R
l
(ρ)
2
dr =1. (14.18)
Since n
=τ −λ −1/2 is a non-negative integer so that we can express the confluent
hypergeometric functions
1
F
1
(−n
;β +1;ρ) by the associated Laguerre polyno-
mial L
β
n
(ρ). Based on Eq. (5.21) and through a direct calculation, we obtain
N
l
=
(M
2
−E
2
)
1/4
(2λ +1)
2(n
+2λ +1)
n
!(2n
+2λ +1)
1/2
,
λ =[(l −1 +D/2)
2
−ξ
2
]
1/2
.
(14.19)
3 Analysis of the Eigenvalues
We now analyze the properties of eigenvalues. It is shown from Eq. (14.14) that
n = 1, 2, 3,... and l = 0, 1,...,n−1. If the principal quantum number n and the
