Dong S.-H. Wave Equations in Higher Dimensions

Подождите немного. Документ загружается.

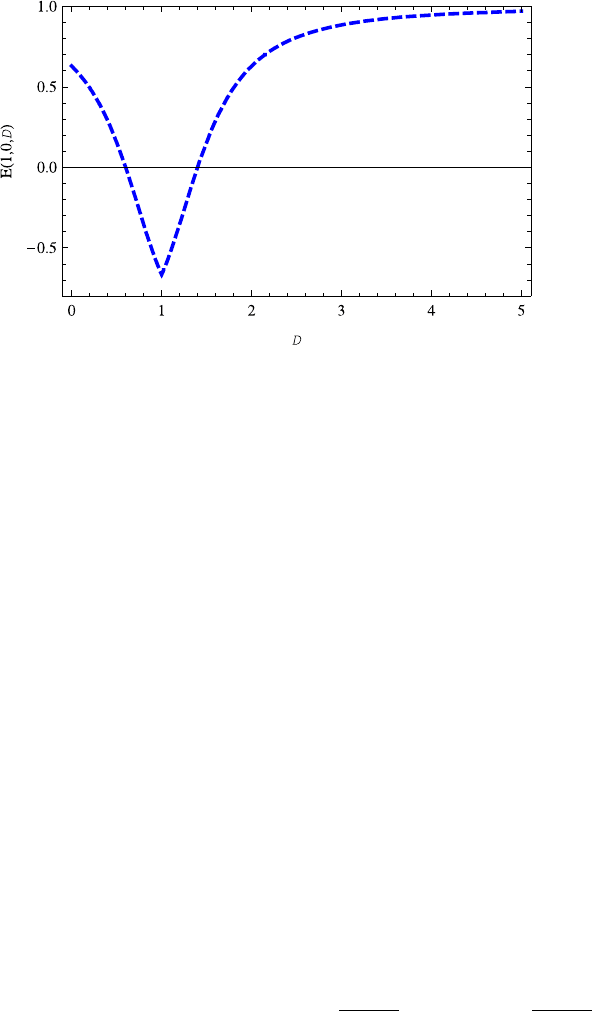
164 13 Dirac Equation with the Coulomb Potential

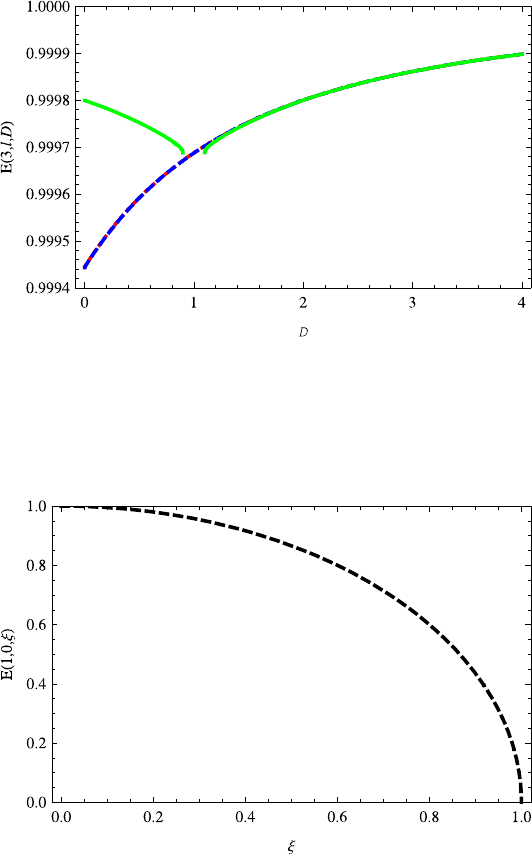
Fig. 13.4 The energy E(1, 0,D) decreases with the increasing dimension D ∈ (0, 0.9],butin-

creases with the increasing dimension D ≥ 1.1. Note that it is symmetric with respect to axis

D =1

Fig. 13.5 The variation of energy E(2, 0,D) (red dotted line) on the dimension D is very similar

to E(1, 0,D). The energy E(2, 1,D) (blue dashed) increases with the increasing dimension D.

Specially, for D>1 the energy E(2, 1,D) almost overlaps E(2, 0,D)

(13.33), i.e., K

≥ξ

. This means that there are no solutions in D ∈(1−2ξ,1+2ξ).

Figure 13.5 shows the properties of E(2,l,D), in which the red dotted and blue

dashed lines correspond to l = 0, 1, respectively. The variation of the E(2, 0,D)

on D is similar to energy E(1, 0,D). But energy E(2, 1,D) increases monoton-

ically as the dimension D increases. It is found that, when D>1 the energies

E(2,l,D) (l = 0, 1) are almost overlapped. This kind of phenomenon occurs in

3 Analysis of the Eigenvalues 165

Fig. 13.6 The variations of energy levels E(3,l,D) (l = 2,1, 0) on dimension D are similar

to E(2,l,D) (l = 1, 0). The energy E(3,2,D) almost overlaps energy E(3, 1,D). This can be

explained well by Eq. (13.28). When D>1, the energies E(3,l,D) (l = 2, 1, 0) are almost

overlapped. The red dotted, blue dashed and green solid lines correspond to quantum numbers

l =2, 1, 0, respectively

Fig. 13.7 The energy E(1, 0,ξ)decreases with the increasing potential parameter ξ ≤1

n = 3(l = 0, 1, 2) as shown in Fig. 13.6. This can be explained well through the

series expansion for 1/D as given in Eq. (13.27).

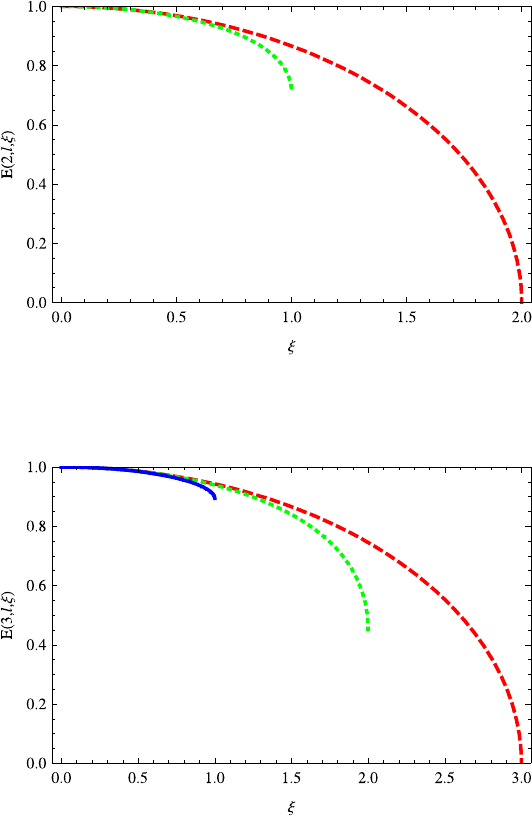
Third, we exhibit the variations of energy E(n,l,ξ) on the potential strength

ξ in Figs. 13.7, 13.8, 13.9. It is found from Fig. 13.7 that the energy E(1, 0,ξ)

decreases with ξ ≤1. This can be explained by Eq. (13.26). That is to say, ξ ≤l +1.

Figures 13.8 and 13.9 show the variations of the E(2,l,ξ) and E(3,l,ξ) on the

166 13 Dirac Equation with the Coulomb Potential

Fig. 13.8 The energies E(2,l,ξ) (l = 0, 1) decrease with the increasing potential parameter ξ.

Notice that ξ ≤1forl =0(green dotted line), while ξ ≤2forl = 1(red dashed line)

Fig. 13.9 The energies E(3,l,ξ)(l =0, 1, 2) decrease with the increasing potential parameter ξ .

Note that ξ ≤ 1forl = 0(blue solid line), while ξ ≤2forl = 1(green dotted line)andξ ≤ 3for

l =2(red dashed line). Generally, the energies E(n,l,ξ) decrease with the potential parameter

ξ ≤l +1foragivenl

potential parameter ξ . The energies E(n,l,ξ) decrease with potential parameter

ξ ≤ l + 1. In Fig. 13.8, the green dotted and red dashed lines correspond to l =

0, 1, respectively. In Fig. 13.9, the blue solid, green dotted and red dashed lines

correspond to l = 0, 1, 2, respectively. Generally, the energies E(n,l,ξ) decrease

with the potential parameter ξ ≤l +1 for a given l.

4 Generalization to the Dirac Equation 167

Fourth, it is worth pointing out the interest of the singularity at |K|=ξ , i.e.,

l +(D −1)/2 = ξ =Zα. This is a famous phenomenon to make the energy formula

broken down for potential strength with Zα ≥ 1 in three dimensions. When the

Dirac equation with the 1/r potential is generalized to the (D + 1)-dimensional

case, however, the singularity survives and moves to big values for Zα, e.g., Zα =

3/2forD =4. Such a kind of phenomenon has been addressed in Ref. [445].

Finally, we want to brieﬂy address the one-dimensional hydrogen atom as dis-

cussed by Moss [189]. The interest arises from its relevance to the behavior of

hydrogen-like atoms in the strong magnetic ﬁelds and to hydrogenic impurities con-

ﬁned in the quantum-well wire structures [188]. It is found that when D = 1 and

Z = 1, the energy spectrum (13.26) does not exist at all since the factor



−ξ

becomes imaginary. This is because from the deﬁnition |K|=l +(D −1)/2, K is

equal to zero regardless of the value of potential parameter ξ if D =1 and l = 0.

This conclusion agrees well with that of Ref. [189].

4 Generalization to the Dirac Equation with a Coulomb

Potential Plus a Scalar Potential

4.1 Introduction

The Dirac equation with a Coulomb potential has been discussed above. Recently,

the bound states and the S-matrix in the quantum scattering theory of the Dirac

equation with a Coulomb plus a scalar potential have been investigated in 3 + 1

dimensions [446–448]. Apart from this, the bound states of the Dirac equation with

the Coulomb plus scalar potential have been carried out both in two dimensions and

in D dimensions [105, 449]. In this section we are going to study the Dirac equation

with a Coulomb potential plus a scalar potential.

4.2 Exact Solutions

We now consider the Dirac equation with a mixed potential including a Coulomb

potential and a scalar potential. The Coulomb potential is taken as

=−

. (13.35)

Also, the scalar potential is chosen as

=−

, (13.36)

which is added to the mass term of the Dirac equation. The v and s denote the

electrostatic and scalar coupling constants, respectively.

168 13 Dirac Equation with the Coulomb Potential

After some algebraic manipulations, we observe that the radial components

(r) and G

(r) satisfy the following ﬁrst-order differential equations [105]

(r) +

(r) =



E −M +

v +s



(r),

−

(r) +

(r) =



E +M +

v −s



(r).

(13.37)

Because this equation keeps invariant by interchanging F

↔ G

−K−E

and

(r) ↔−V

(r), we only discuss the attractive Coulomb potential case V

(r)

(v>0). The solutions for the repulsive Coulomb potential V

(r) (v<0) can be

obtained from the former by interchanging F

↔ G

−K−E

. The scalar potential

, however, has to be discussed by two different cases s>0 and s<0.

Likewise, we introduce ρ = 2r

√

−E

for the bound states |E| <M. Thus,

Eq. (13.37) becomes

(ρ) +

(ρ) =



−



M −E

M +E

v +s



(ρ),

(ρ) −

(ρ) =



−



M +E

M −E

−

v −s



(ρ).

(13.38)

Similarly, deﬁne the wavefunction 

(ρ) with the forms

(ρ) =

√

M −E [

(ρ) +

−

(ρ)],

(ρ) =

√

M +E [

(ρ) −

−

(ρ)].

(13.39)

Substitution of them into Eq. (13.38) leads to

dρ



(ρ) ±

dρ



−

(ρ) ±

[

(ρ) ±

−

(ρ)]



−

v ±s



M ±E

M ∓E



[

(ρ) ∓

−

(ρ)]. (13.40)

Their addition and subtraction allow us to obtain

dρ



(ρ) ∓



vE +sM

√

−E

−





(ρ)

=−



vM +sE

√

−E





∓

(ρ). (13.41)

Take the following conventions

τ =

vE +sM

√

−E

,τ



vM +sE

√

−E

. (13.42)

Then, Eq. (13.41) is simpliﬁed to

dρ



(ρ) ∓



−





(ρ) =∓



±K



∓

(ρ). (13.43)

4 Generalization to the Dirac Equation 169

Based on this relation, we are able to obtain the following important second-order

differential equations



dρ



−

τ ±1/2

−





(ρ) =0, (13.44)

where

−v

. (13.45)

For a weak Coulomb potential, we take

λ =



−v

> 0. (13.46)

From the behaviors of the wavefunction at the origin and at inﬁnity, we deﬁne



(ρ) =ρ

−ρ/2

(ρ). (13.47)

Substitution of this into (13.44) yields

dρ

(ρ) +



−1 +

1 +2λ



dρ

(ρ)

τ −λ −1/2 ±1/2

(ρ) =0, (13.48)

whose solutions are the conﬂuent hypergeometric functions

(ρ) =a

(λ −τ ;2λ +1;ρ),

−

(ρ) =b

(1 +λ −τ ;2λ +1;ρ).

(13.49)

Let us study the relation between a

and b

. With the same technique as above,

we have



λ −τ





(1 +λ −τ ;2λ +1;ρ) =0. (13.50)

Since both a

and b

are not equal to zero, we obtain

τ −λ



. (13.51)

From Eq. (13.39) one has

(ρ) = N

√

M −Eρ

−ρ/2

×[(τ



+K)

(λ −τ ;2λ +1;ρ)

+(τ −λ)

(1 +λ −τ ;2λ +1;ρ)],

(ρ) = N

√

M +Eρ

−ρ/2

×[(τ



+K)

(λ −τ ;2λ +1;ρ)

−(τ −λ)

(1 +λ −τ ;2λ +1;ρ)],

(13.52)

Notice that Eq. (13.44) is a special case of the Tricomi equation as given in Eq. (13.14).

170 13 Dirac Equation with the Coulomb Potential

where N

(τ



+K)

−1

√

−E

)

−1/2

We now study the eigenvalues of this quantum system. The quantum condition is

given by

τ −λ =n



=0, 1, 2,.... (13.53)

When n



=0, λ =τ , and

=τ

−s

=(τ



)

. (13.54)

Therefore, K has to be positive to avoid a trivial solution.

Introduce a principal quantum number

n =|K|−(D −3)/2 +n



=|K|−(D −3)/2 +τ −λ

=l +1 +n



=1, 2,.... (13.55)

BasedonEqs.(13.42) and (13.53), we have

Ev +Ms

√

−E

=n −|K|+

D −3

+λ =n



+λ =n −l −1 +λ ≡κ. (13.56)

The energy E can be solved from Eq. (13.56)

E(n,l,D) =M



−

+κ



+κ



−

−κ

+κ



1/2



. (13.57)

We now consider a few special cases. First, if v =0, then λ =

√

. Thus,

the energy becomes

E(n,l,D) =±M



1 −

(n −l −1 +

√

)



1/2

. (13.58)

It implies that there are two branches of symmetric solutions for the positive and

negative energies.

For a large D,wehave

E(n,D) ±M[1 −2s

−2

+4s

(2n −3)D

−3

−···], (13.59)

which implies that the energy is independent of l for a large D.

For a small s,wehave

E(n,l,D) ±M



1 −

2[n +(D −3)/2]



2n +D −3

2l +D −1

−



, (13.60)

where the ﬁrst term on the right hand side is the rest energy M (c

=1), the second

one is from the solutions of the Schrödinger equation, and the third one is the ﬁne

structure energy, which removes the degeneracy between the states with the same n.

On the other hand, it is shown from λ given in (13.46) that the scalar potential

parameter s can be taken arbitrarily for the vector potential parameter v =0.

4 Generalization to the Dirac Equation 171

Second, if s =0, then λ =

√

−v

. It is found from Eq. (13.46) that E has

thesamesignasv when K

. For the attractive Coulomb potential (v>0) we

have the positive energy E(n,l,D)

E(n,l,D) =M



1 +

(n −l −1 +

√

−v

)



−1/2

. (13.61)

This coincides with the conclusion from the Sturm-Liouville theorem for a weak

attractive potential [184, 247, 248]. For a large D we have the similar result as

Eq. (13.59)(s is replaced by v).

For a small v,wehave

E(n,l,D) M

|v|



1 −

2[n +(D −3)/2]

−

2[n +(D −3)/2]



2n +D −3

2l +D −1

−



. (13.62)

Similarly, the physical meanings of three terms are similar to those of Eq. (13.60)

except for the different expansion coefﬁcients. This case has been studied in our

recent work [104, 450], to which the reader can refer for more information.

Third, if v = s, from Eq. (13.56) both v and s have to be positive, λ =|K|, and

the positive κ is given by

κ =n −l −1 +|K|=



n +

D−3

, when K ≥0,

n −2l −

1+D

, when K<0.

(13.63)

The energy is written as

E(n,l,D) =

⎧

⎪

⎨

⎪

⎩

M{1 −

+(n+

D−3

)

}, for K ≥0,

M{1 −

+(n−2l−

1+D

)

}, for K<0,

(13.64)

which implies that the energy is independent of the angular momentum quantum

number l for K ≥0, but for K<0 it depends upon l. If we choose the negative sign

in the result, we have E =−M, which is a singular solution of Eq. (13.56).

We now determine the normalization factor N

from the normalization condi-

tion



†



dV =1. (13.65)

Similarly, through a direct calculation we get

−E

)

1/4

(2λ +1)



(τ +λ +1)

2Mτ



(K +τ



)(τ −λ)!



1/2

. (13.66)

172 13 Dirac Equation with the Coulomb Potential

Fig. 13.10 The energy E(1,0,D) decreases with the increasing dimension D ∈ (0, 1),butin-

creases with the increasing dimension D ≥1. The parameters v =0.2ands =0.3aretakenhere

andalsoinFigs.13.11 and 13.12

4.3 Analysis of the Energy Level

We now analyze the variation of the energy E(n,l,D) on the dimension D.Itis

shown from Eqs. (13.46) and (13.56) that the energy E(n,l,D) giveninEq.(13.57)

is closely related with the following two conditions,

,Ev+Ms > 0, (13.67)

from which we can determine whether the energy is positive or negative. Recall that

we only consider the case with positive v. For the case of negative v, the energy

E(n,l,D) changes its sign. For simplicity, we take sign “+” for the second term

in Eq. (13.57). In fact, the energy levels are also valid if we take sign “−”forthe

second term, while the variations shall change with the different choice of the signs.

First, we consider the case s>0. We discuss the energy E(n,l,D) in two cases

s>vand s<v. For the ﬁrst case s>v, due to Eq. (13.67) the bound states with

0 <E<M are physically acceptable. We take v =0.2 and s =0.3 for the weak at-

tractive Coulomb potential. It is shown in Figs. 13.10, 13.11, 13.12 that the energies

E(n,0,D) ﬁrst decrease for D ∈ (0, 1) and then increase with the increasing di-

mension D ≥1, while the energies E(n,l,D) (l =0) are almost independent of the

quantum number l. Also, the energies E(n,l,D) are almost overlapped for a large

D. It is shown that the energies E(n,0,D) are symmetric with respect to D = 1

for D ∈ (0, 2). For the second case s<v,wetake

v = 0.3 and s =0.2. It is found

that there does not permit bound state for l = 0 and D ∈ (0.55, 1.45). This can

be explained well from Eq. (13.46), i.e., ((D −1)/2)

≥v

for l = 0. Conse-

quently, there exist the bound states for D ≥1+2

√

−s

and D ≤1−2

√

−s

The corresponding variations of energies E(n,l,D) on the dimension D are il-

lustrated in Figs. 13.13, 13.14, 13.15, 13.16. It is shown in Fig. 13.13 that the

4 Generalization to the Dirac Equation 173

Fig. 13.11 The variation of energy E(2, 0,D) (red dashed line) on the dimension D is similar to

E(1, 0,D). The energy E(2, 1,D)(blue solid line) increases with the dimension D.ForD>2the

energy E(2, 1,D) almost overlaps E(2, 0,D)

Fig. 13.12 The variations of energy levels E(3,l,D) (l = 2, 1, 0) on dimension D are similar

to E(2,l,D) (l =1, 0). The energy E(3, 2,D) almost overlaps energy E(3, 1,D).ForD>2, the

energies E(3,l,D)(l =2, 1, 0) are almost overlapped. The blue dotted, green dashed and red solid

lines correspond to l =0, 1, 2, respectively

energy E(1, 0,D) decreases with the increasing dimension D ∈ (0, 0.55],butin-

creases with the increasing dimension D ≥ 1.45. There does not exist bound state

for D ∈ (0.55, 1.45). It is shown in Figs. 13.15 and 13.16 that the variations of en-

ergies E(n,0,D)(n =2, 3) are very similar to E(1, 0,D). The energies E(n,1,D)

(n = 2, 3) increase with the dimension D. Note that the energies E(n,l,D) are al-