Долгіх В.М. Математика для економістів - Математичний аналіз. Диференціальне числення
Подождите немного. Документ загружается.


ДВНЗ “Українська академія банківської справи НБУ”
61
Рис. 3.2
Якщо спроектувати всі точки цієї поверхні на площину ,
x
O
y
отримаємо круг з радіусом 1 і з центром у початку координат. А це і є
областю визначення функції
.1
22
yxz −−=
Поверхня, яка відповідає рівнянню ),,( y
x
f
z
=
проектуватиметь-
ся на площину
x
O
y
в область визначення цієї функції.
Графік функції двох змінних значно складніше, ніж графік функ-
ції однієї змінної. Тому існує спосіб зображення функції двох змінних,
який полягає в перетині поверхні ),( y
x
f
z
=
площинами z = C (C –
довільне число ), паралельними площині
x
O
y
.
Лінією рівня C називається множина точок ),( y
x
площини
x
O
y
,
в яких функція набуває одного й того самого значення C і визначаєть-
ся співвідношенням .),(
C
y
x
f
=
Приклад 3.3. Побудувати графік функції
.1
22
+
+
=
yxz
► Лінією нульового рівня є точка ),0;0( лінією першого рівня є
коло з центром у початку координат і радіусом 1. Сім’ю деяких ліній
рівня цієї функції зображено на рис. 3.3.
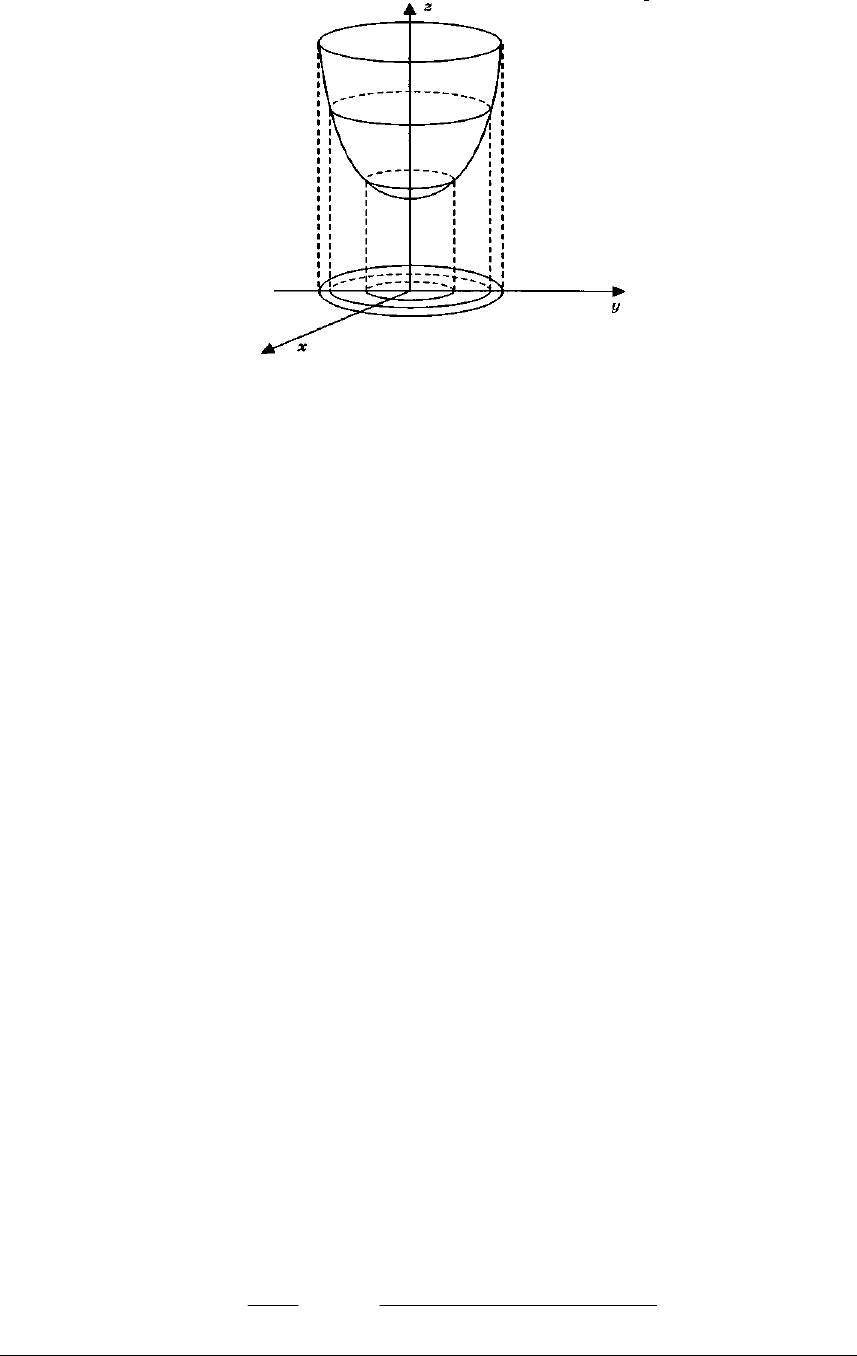
Рис. 3.3
Якщо тепер кожну лінію рівня розмістити у відповідній площині,
то отримаємо зображення графіка функції (рис. 3.4).
ДВНЗ “Українська академія банківської справи НБУ”
62
Рис. 3.4
Функції трьох і більше змінних зобразити графічно неможливо.
3.2. ГРАНИЦЯ І НЕПЕРЕРВНІСТЬ ФУНКЦІЇ
БАГАТЬОХ ЗМІННИХ
Число А називається границею функції ),( y
x
f
z
=
у точці
0
M
,
якщо для будь-якої збіжної до ),(
000
yxM послідовності точок
...,...,,,
21 n
MMM
),(
0
DMMM
nn
∈
≠
відповідна послідовність зна-
чень функції ...),(...,),(),(
21 n
MfMfMf збігається до А.
Коротко це записують так:
.),(limабо,)(lim
0
00
AyxfAMf
yy
xxMM
=
=
→
→→
(3.1)
Функція ),( y
x
f
z = називається неперервною в точці
0
M , якщо
границя функції в цій точці існує і дорівнює значенню функції в цій
точці, тобто
),()(lim
0
0
MfMf
MM
=
→
або
).,(),(lim
00
0
0
yxfyxf
yy
xx
=
→
→
(3.2)
3.3. ЧАСТИННІ ПРИРОСТИ ТА ЧАСТИННІ ПОХІДНІ
Припустимо, що задані функція ),( y
x
f
z
=
і точка .),( Dy
x
∈
Якщо зміна функції z відбувається при зміні тільки одного з аргумен-
тів, наприклад х, при фіксованому значенні другого аргументу у, то
функція набуває приросту ),,(),( yxfyxxfz
x
−
Δ
+
=
Δ
який називаєть-
ся частинним приростом функції ),( y
x
f
за аргументом x.
Якщо існує скінченна границя
,
),(),(
limlim
00
x
yxfyxxf
x
z
Δx
x
Δx
Δ
−
Δ
+
=
Δ
Δ
→→
(3.3)

ДВНЗ “Українська академія банківської справи НБУ”
63
то вона називається частинною похідною функції ),( y
x
f
за аргумен-
том х і позначається одним із символів:
.,,
x
f
x
f
x
z
′
∂
∂
∂
∂
Аналогічно дається означення частинного приросту
z за аргу-
ментом у і частинної похідної ),( y
x
f
за аргументом y:
.
),(),(
lim
0
y
yxfyyxf
y
z
y
Δ
−
Δ
+
=
∂
∂
→Δ
(3.4)
Під час обчислення частинних похідних користуються вже ві-
домими правилами і формулами диференціювання функції однієї
змінної, вважаючи при цьому другу змінну сталою.
Приклад 3.4. Знайти частинні похідні функції
y
x
z arccos=
).0( >y
► Вважаємо величину y сталою, маємо:
.
11
)/(1
1
222
xy
y
yx
x
z
−
−=
−
−=
∂
∂
Вважаємо величину x сталою, маємо:
.
1
)/(1
1
22
2
2
xy
y
x
y
x
yx
y
z
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
−=
∂
∂
Аналогічно даються поняття частинних похiдних функцій трьох і
більше змінних.
Частинні похідні функції декількох змінних визначаються і обчи-
слюються також у припущенні, що змінюється тільки одна з незалеж-
них змінних, а інші при цьому фіксовані.
Частинна похідна функції кількох змінних має той же механічний
зміст, що і похідна функції
однієї змінної – це швидкість зміни функ-
ції відносно зміни одного з аргументів.
3.4. ПОХІДНА ЗА ДАНИМ НАПРЯМОМ.
ГРАДІЄНТ ФУНКЦІЇ ДЕКІЛЬКОХ ЗМІННИХ
Частинні похідні дають “швидкість зміни” функції ),( y
x
f
у на-
прямах, паралельних координатним осям. Проте часто буває, що потрібно
знайти швидкість зміни ),( y
x
f
в будь-якому напрямі. Диференційована
функція, як побачимо далі, має похідну в довільному напрямку.

ДВНЗ “Українська академія банківської справи НБУ”
64
На довільній осі l візьмемо фіксовану точку ),( y
x
M
і змінну то-
чку ).,( yy
x
x
P
Δ+Δ+ Позначимо через
ϕ
кут, який утворює вісь l з
віссю ,Ox а через
ρ
– відстань від точки P до точки M (рис. 3.5):
Рис. 3.5
Якщо існує границя відношення
,
),(),(
lim
ρ
yxfyyxxf
MP
−
Δ
+
Δ
+
→
(3.5)
коли точка P по осі l наближається до M, то цю границю називають по-
хідною від функції ),( y
x
f
у точці M за напрямом l і позначають .
l
f
∂
∂
Припустимо, що ),( y
x
f
має неперервні частинні похідні
x
f
∂
∂
і
y
f
∂
∂
.
Точка
P
наближається до
M
по прямій
,
l
отже,
.sin,cos
ϕ
ρ
ϕ
ρ
=Δ=Δ y
x
Таким чином,
.sin),(cos),(
),(),(
lim
0
ϕϕ
ρ
ρ
yxfyxf
yxfyyxxf
yx
′
+
′
=
−
Δ
+
Δ+
→
Отже, за умов, накладених вище на частинні похідні, границя
(2.50) існує, тому остаточно
.sin),(cos),(
ϕϕ
yxfyxf
l
f
yx
′
+
′
=
∂
∂
(3.6)
Ця формула є формулою похідної за даним напрямом.
У фіксованій точці ця похідна є функцією кута .
ϕ
Виникає пи-
тання: в якому ж напрямі похідна має найбільшу величину, тобто в
якому напрямку функція ),( y
x
f
зростає найшвидше?

ДВНЗ “Українська академія банківської справи НБУ”
65
Вектор ,
→
g який має за проекції на координатних осях
x
f
∂
∂
і
y
f
∂
∂
та
вказує напрям найшвидшого зростання функції ),,( y
x
f
називається
градієнтом функції в точці M і позначається
.),(
→→→
∂
∂
+
∂
∂
== j
y
f
i
x
f
yxfgradg
(3.7)
Якщо б ми розглядали функцію від трьох змінних ),,,( zy
x
f
u =
то для похідної за напрямком дістали б:
,cos),,(cos),,(cos),,(
γβα
zyxfzyxfzyxf
l
f
zyx
′
+
′
+
′
=
∂
∂
(3.8)
де
γ
β
α
cos,cos,cos є напрямними косинусами .
l
А для градієнта в цьому випадку мали б:
.),,(
→→→→
∂
∂
+
∂
∂
+
∂
∂
== k
z
f
j
y
f
i
x
f
zyxfgradg
(3.9)
Геометрично напрямок градієнта функції співпадає із напрямком
найшвидшого зростання величини, що задається цією функцією, а
його модуль дорівнює частинній похідній цієї функції за даним на-
прямком.
В економіці градієнт використовується під час розв’язання задач
оптимізації.
3.5. ЧАСТИННІ ПОХІДНІ ВИЩИХ ПОРЯДКІВ
Частинними похідними другого порядку функції ),( y
x
f
z
=
на-
зиваються частинні похідні від її частинних похідних першого порядку,
якщо вони існують.
Частинні похідні другого порядку позначаються так:
;
2
2
xx
f
x
f
x
f
x
′′
=
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
;
2
xy
f
yx
f
x
f
y
′′
=
∂∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
;
2
yx
f
xy
f
y
f
x
′′
=
∂∂
∂
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
.
2
2
yy
f
y
f
y
f
y
′′
=
∂
∂
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
Аналогічно визначаються частинні похідні більш високого порядку.
Частинна похідна другого або більш високого порядку, взята за деякими
різними змінними, називається мішаною частинною похідною.
Теорема. Дві мішані частинні похідні однієї й тієї ж функції,
що відрізняються лише порядком диференціювання, дорівню-
ють одна одній за умови їх неперервності

ДВНЗ “Українська академія банківської справи НБУ”
66
Приклад 3.5. Знайдемо частинну похідну
xyx
z
∂∂∂
∂
3
від функції
).sin(cos yxyez
x
+
=
► Маємо:
),sinsin(cos yxyye
x
z
x
++=
∂
∂
),cossin(cos
2
yxyye
x
z
yx
z
x
y
+−=
′
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
∂∂
∂
).cossincos2(
23
yxyye
yx
z
xyx
z
x
x
+−=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂∂
∂
=
∂∂∂
∂
3.6. ПОВНИЙ ПРИРІСТ. ПОВНИЙ ДИФЕРЕНЦІАЛ ФУНКЦІЇ
БАГАТЬОХ НЕЗАЛЕЖНИХ ЗМІННИХ І ЙОГО ЗАСТОСУВАННЯ
Дано функцію двох змінних ).,( y
x
f
z
=
Припустимо, що її аргу-
менти x і y отримують прирости
x
Δ
і .y
Δ
Тоді функція ),( y
x
f
z =
отримує повний приріст
).,(),( y
x
f
yy
x
x
f
z
−
Δ
+
Δ
+
=Δ (3.10)
Геометрично повний приріст
z
Δ
дорівнює приросту аплікати
графіка функції ),( y
x
f
при переході від точки ),( y
x
M
у точку
).,(
1
yyxxM
Δ
Δ
+
+
Функція ),( y
x
f
z = називається диференційованою в точці ),,( y
x
якщо її повний приріст
zΔ може бути поданий у вигляді:
),(),(),(
ρ
oyy
x
B
x
y
x
A
z
+
Δ
+
Δ
=Δ
де
;)()(
22
yx Δ+Δ=
ρ
)(
ρ
o
– нескінченно мала більш високого порядку, ніж .
ρ
Якщо функція ),( y
x
f
z = диференційована в даній точці, то її
повним диференціалом називається головна частина повного приросту
цієї функції, лінійна відносно
x
Δ
і ,y
Δ
тобто
.),(),( yy
x
B
x
y
x
A
dz
Δ
+
Δ
=
Диференціали незалежних змінних, за означенням, дорівнюють їх
приростам
,
x
dx Δ= .ydy
Δ
= Диференціал функції ),( y
x
f
z = обчис-
люється за формулою:
.dy
y
z
dx
x
z
dz
∂
∂
+
∂
∂
=
(3.11)
Якщо замінимо наближено приріст функції її диференціалом (у
припущенні достатньої малості значень
x
Δ
і ),y
Δ
отримаємо:

ДВНЗ “Українська академія банківської справи НБУ”
67
.),(),( dyyxfdxyxfdzz
yx
′
+
′
=≈Δ (3.12)
Звідки маємо:
.),(),(),(),(),( dyyxfdxyxfyxfdzyxfyyxxf
yx
′
+
′
+
=
+
≈Δ+Δ+
Усі ці міркування можна перенести на функції трьох і більше
змінних.
Приклад 3.6. Обчислити наближено
).1998,0003,1ln(
4
3
−+
► Шукане число розглядатимемо як значення функції
)1ln(),(
4
3
−+= yxyxf при ,
0
xxx
Δ
+
=
,
0
yyy
Δ
+
=
якщо ,1
0
=x
,1
0
=y ,003,0=Δ
x
.002,0−=
Δ
y Застосуємо формулу
,),(),(),(),(
00000000
dyyxfdxyxfyxfyyxxf
yx
′
+
′
+
≈Δ+Δ+
маємо
,0)111ln(),(
4
3
00
=−+=yxf
,
3
1
1
1
3
1
111
1
),(
3
2
4
3
00
=⋅⋅
−+
=yxf
'
x
.
4
1
1
1
4
1
111
1
),(
4
3
4
3
00
=⋅⋅
−+
=yxf
'
y
Отже,
.0005,0)002,0(
4
1
003,0
3
1
0)198,003,1ln(
4
3
=−⋅+⋅+≈−+
3.7. ДИФЕРЕНЦІЮВАННЯ СКЛАДЕНИХ ФУНКЦІЙ
Випадок однієї незалежної змінної
Якщо функція ),( y
x
f
z = є диференційованою функцією двох змін-
них x і y, а аргументи цієї функції самі є диференційованими функціями
незалежної змінної t: )(
t
x
ϕ
= і ),(
t
y
ψ
=
тоді складена функція
))(),((
t
t
f
z
ψ
ϕ
= диференційована, її похідна обчислюється за формулою
.
dt
dy
y
z
dt
dx
x
z
dt
dz
⋅
∂
∂
+⋅
∂
∂
=
(3.13)
Припустимо тепер, що ),,( y
x
f
z = де ).(
x
y
ϕ
=
Тоді )),(,(
x
x
f
z
ϕ
=
тобто функція z є функцією однієї змінної x. Цей випадок зводиться до
попереднього, де роль змінної t відіграє x, “повна” похідна функції z
за змінною x дорівнює
.
dx
dy
y
z
x
z
dx
dz
⋅
∂
∂
+
∂
∂
=
Приклад 3.7. Знайти
,
dt
dz
якщо ,
52 yx
ez
+
=
де
,sin
t
x
=
.
3
ty =

ДВНЗ “Українська академія банківської справи НБУ”
68
► Маємо
,2
52 yx
e
x
z
+
=
∂
∂
,5
52 yx
e
y
z
+
=
∂
∂
,cost
d
t
dx
=
;3
2
t
d
t
dy
=
).15cos2(35cos2
25sin225252
3
ttetete
d
t
dz
ttyxyx
+=⋅+⋅=
+++
Приклад 3.8. Знайти частинну похідну
x
z
∂
∂
й повну похідну
,
dx
dz
якщо
,
3xy
ez = а .4
2
+= xy
► Маємо
,3
3xy
ey
x
z
⋅=
∂
∂
,3
3xy
xe
y
z
=
∂
∂
,
4
2
+
=
x
x
dx
dy
.
4
)2(
6
4
33
2
2
43
2
33
2
+
+
⋅=
+
⋅⋅+⋅=
+
x
x
e
x
x
exey
dx
dz
xxxyxy
Випадок декількох незалежних змінних
Припустимо тепер, що ),,( y
x
f
z
=
де ),(
v
u
x
ϕ
=
і ).,(
v
uy
ψ
=
Тоді
z є складеною функцією двох незалежних змінних u і .
v
Час-
тинні похідні цієї складеної функції знаходять за формулами:
,
u
y
y
z
u
x
x
z
u
z
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
=
∂
∂
.
v
y
y
z
v
x
x
z
v
z
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
=
∂
∂
Ці формули узагальнюються для випадку складеної функції будь-
якого скінченного числа аргументів. У всіх випадках справедлива фо-
рмула:
.dy
y
z
dx
x
z
dz ⋅
∂
∂
+⋅
∂
∂
=
(3.14)
Формула (3.14) відображає властивість інваріантності форми по-
вного диференціала.
3.8. НЕЯВНІ ФУНКЦІЇ ТА ЇХ ДИФЕРЕНЦІЮВАННЯ
Припустимо, що F – диференційована функція змінних x, y, z і рі-
вняння 0),,( =zy
x
F визначає z як функцію незалежних змінних x і y.
Частинні похідні цієї неявної функції ),( y
x
zz
=
у точці ),( y
x
обчис-
люються за формулами:
;
),,(
),,(
zyxF
zyxF
x
z
z
x
′
′
−=
∂
∂
.0),,(,
),,,(
),,(
≠
′
′
′
−=
∂
∂
zyxF
zyxF
zyxF
y
z
z
z
y
(3.15)

ДВНЗ “Українська академія банківської справи НБУ”
69
Приклад 3.9. Знайти частинні похідні
x
z
∂
∂
і
,
y
z
∂
∂
якщо z визначається
як функція від x і y з рівняння
.0124
223
=
+
−
−
zxyz
► Позначимо ліву частину даного рівняння через ).,,( zy
x
F
Тоді
,4),,(
2
yzyxF
x
−
=
′
,8),,( xyzyxF
y
−
=
′
.43),,(
2
zzzyxF
z
−
=
′
Звідси маємо
;
43
4
),,(
),,(
2
2
zz
y
zyxF
zyxF
x
z
z
x
−
=
′
′
−=
∂
∂
.
43
8
),,(
),,(
2
zz
xy
zyxF
zyxF
y
z
z
z
−
=
′
′
−=
∂
∂
3.9. ЕКСТРЕМУМИ ФУНКЦІЙ ДВОХ ЗМІННИХ
Функція );( y
x
f
z = має максимум (мінімум) в точці
),,(
000
yxM
як-
що для будь-якої точки ),,( y
x
M
що знаходиться у деякому
δ
-околі точ-
ки
),,(
000
yxM
виконується умова:
));,(),((),,(),(
0000
yxfyxfyxfyxf <>
δ
-окіл точки ),(
000
yxM можна подати як множину точок ),,( y
x
M
координати яких задовольняють умову
,)()(
2
0
2
0
δ
<−+− yyxx де
δ
–
додатне досить мале число.
Максимуми та мінімуми функції називають екстремумами, а то-
чку ),(
000
yxM – точкою екстремуму.
Теорема 1. Якщо );( y
x
f
z = – диференційована й досягає в
точці ),(
000
yxM екстремуму, то її частинні похідні першого
порядку в цій точці дорівнюють нулю
Точки, в яких частинні похідні першого порядку обертаються в
нуль (або не існують) називаються стаціонарними (або критичними).
Припустимо, що ),(
000
yxM – стаціонарна точка функції
).;( y
x
f
z = Позначимо частинні похідні другого порядку так:
.
)(
;
)(
;
)(
0
2
2
0
2
2
0
2
B
yx
Mz
C
y
Mz
A
x
Mz
=
∂∂
∂
=
∂
∂
=
∂
∂
Визначник
2
B
AC
−
=
Δ називається гессіаном.
Теорема 2. Якщо функція );( y
x
f
z
=
– неперервна разом зі
своїми похідними першого та другого порядку, і точка
),(
000
yxM є стаціонарною точкою, то якщо:
1)
,0>Δ
то точка ),(
000
yxM – точка екстремуму, при 0>
A
99(або 0>
C
при 0
=
A
) у точці ),(
000
yxM функція має
ДВНЗ “Українська академія банківської справи НБУ”
70
мінімум, а якщо 0
<
A
(або 0
<
C
при 0=
A
) у точці
),(
000
yxM функція має максимум;
2) ,0
<
Δ то точка
),(
000
yxM
– не є точкою екстремуму;
3) ,0
=
Δ то потрібні додаткові дослідження.
Приклад 3.10. Знайти екстремум функції
.25
2
1
2
2
3
22
+−−−+= yxyxyxz
► Знайдемо частинні похідні:
.12;523 −−=
∂
∂
−+=
∂
∂
yx
y
z
yx
x
z
Знаходимо стаціонарні точки:
⎩
⎨
⎧
=−−
=
−
+
.012
,0523
yx
yx
Точка )1;1(
0
M – стаціонарна.
Знайдемо значення других похідних
.2
)(
;1
)(
;3
)(
0
2
2
0
2
2
0
2
=
∂∂
∂
−=
∂
∂
=
∂
∂
yx
Mz
y
Mz
x
Mz
Отже, знак гессіана
,072)1(3
2
<
−
=
−
−
=
Δ
тобто в точці )1;1(
0
M
функція не має екстремуму.
3.10. НАЙБІЛЬШЕ І НАЙМЕНШЕ ЗНАЧЕННЯ ФУНКЦІЇ,
НЕПЕРЕРВНОЇ У ЗАМКНЕНІЙ ОБМЕЖЕНІЙ ОБЛАСТІ.
УМОВНИЙ ЕКСТРЕМУМ ФУНКЦІЇ ДВОХ ЗМІННИХ.
МЕТОД МНОЖНИКІВ ЛАГРАНЖА
Функція ),;( y
x
f
z = диференційована в обмеженій області, на-
буває в ній найбільшого та найменшого значень у стаціонарних точ-
ках або в граничних точках. Таким чином, щоб знайти найбільше і
найменше значення функції в замкненій області, необхідно:
1)
знайти стацiонарнi точки, розмiщенi в даній області, i обчислити
значення функції в цих точках;
2)
дослідити функцію на екстремум на межі області;
3)
з усix знайдених значень обрати найбільше i найменше.
Приклад 3.11. Знайти найбільше і найменше значення функції
z = x
2
+ 2y
2
– 2x – 8y + 4 в замкненому трикутнику АОВ, обмеженому
осями координат i прямою х + у – 4 = 0 (рис. 3.6).
► Знайдемо частинні похідні:
.84;22 −=
∂
∂
−=
∂
∂
y
y
z
x
x
z
