Долгіх В.М. Математика для економістів - Математичний аналіз. Диференціальне числення
Подождите немного. Документ загружается.


ДВНЗ “Українська академія банківської справи НБУ”
51
Приклад 2.13. Визначимо тип екстремуму функції y = x³ – 3x
2
+ 7
при
х = 1.
► Точка х = 1 є критичною, оскільки y′ = 3x² – 3x = 0 при х = 1.
Оскільки при
x < 1 y′ < 0, а при x > 1 y′ > 0, x = 1 – точка мінімуму.
Можна було б встановити цей факт за допомогою другої похідної:
y′′ = 6x – 3; y′′(1) = 3 > 0. Отже, функція в цій точці досягає мінімуму
(теорема 4).
Приклад 2.14. Дослідимо на екстремум функцію y = x
5
+ x
3
.
► y′ = 5x
4
+ 3x² = x²(5x² + 3) = 0 при х = 0. При цьому y′′ = 20x³ +
+ 6x = 0 при х = 0, y′′′ = 60x² + 6 = 6 ≠ 0 при х = 0. Порядок першої
ненульової похідної у точці
х = 0 дорівнює непарному числу 3, отже,
за теоремою 5 функція не має екстремуму в цій точці, а оскільки кри-
тична точка єдина, функція взагалі не має екстремумів.
2.16.3. Найбільше та найменше значення функції
Припустимо, що функція y = f(x) диференційована на відрізку [a, b].
Тоді за теоремою 2 пункту 2.2 вона неперервна на ньому і за теоре-
мою Вейєрштрасса досягає на цьому відрізку свого найбільшого та
найменшого значень. Якщо
f(x) має на [a, b] скінченну кількість кри-
тичних точок, то її найбільше значення буде або одним із її максиму-
мів (а саме – найбільшим максимумом) або досягатиметься в одній із
кінцевих точок відрізка. Те ж саме можна сказати й про найменше
значення. Отже, пошук найбільшого та найменшого значень диферен-
ційованої функції на відрізку можна проводити
за такою схемою:
1)
знайти критичні точки функції, що належать даному відрізку;
2)
обчислити значення функції в точках а і b, а також у знайдених
критичних точках. Найменше з отриманих чисел буде найменшим
значенням функції на даному відрізку, а найбільше – її найбільшим
значенням на ньому.
Приклад 2.15. Знайдемо найбільше та найменше значення функції
y = x³ +3x² – 9x – 15 на відрізку [– 4, 4].
► Знайдемо похідну й прирівняємо її до нуля:
y′ = 3x² + 6x – 9 = 0 при х = –3 й х = 1.
При цьому обидві знайдені критичні точки належать даному від-
різку. Обчислимо значення функції: при
х = –4, х = –3, х = 1 і х = 4:
у(–4) = 5, у(–3) = 12, у(1)= –20, у(4) = 61.
Отже, найбільше значення функції на відрізку [–4, 4] дорівнює 61
і досягається на його правій межі, а найменше значення дорівнює
(–20) і досягається в точці мінімуму всередині відрізка.

ДВНЗ “Українська академія банківської справи НБУ”
52
2.16.4. Опуклість функції, точки перегину
Крива називається опуклою (вгнутою) в деякій точці М, якщо в
околі цієї точки лежить під(над) дотичною, проведеною в точці
М.
На рис. 2.4 у точці
1
M крива опукла, а в
2
M – вгнута (припуска-
ється, що
f(x), графік якої подано на цьому рисунку, має неперервну
другу похідну).
Рис. 2.4
Крива називається опуклою (вгнутою) на деякому проміжку, як-
що вона опукла (вгнута) в усіх точках цього проміжку.
Теорема 6. Якщо f′′(x) < 0 у всіх точках інтервалу (a, b), тоді
крива y = f(x) опукла на цьому інтервалі. Якщо f ′′(x) > 0 у всіх
точках інтервалу (a, b), то крива y = f(x) вгнута на цьому
інтервалі
Подамо лише деякі міркування геометричного характеру. Якщо
на проміжку (
a, b) f ′′(x) < 0, то це означає, що функція f ′(x) спадна.
Отже, спадає кутовий коефіцієнт дотичної )tg(
α
до кривої і, звичай-
но, спадає й кут ,
α
утворюваний дотичною з віссю Ох (рис. 2.5).
Рис. 2.5
Рис. 2.6
Очевидно, крива в усіх точках проміжку (a, b) розташована під
дотичною, тобто вона опукла.
Якщо
f ′′(x) > 0, то такі самі геометричні міркування доводять, що
крива буде вгнутою (рис. 2.6).
Точка, що відокремлює опуклу частину неперервної кривої від
вгнутої, називається
точкою перегину.
Зауваження. У точці перегину дотична до кривої, перетинає кри-
ву, тому що з одного боку від даної точки крива проходить вище до-
тичної, а з іншого – нижче.

ДВНЗ “Українська академія банківської справи НБУ”
53
Теорема 7 (необхідна умова точки перегину). Якщо в точці x
0
перегину кривої, що є графіком функції y = f(x), існує друга по-
хідна f ′′(x), то f′′(x
0
) = 0
Z Оскільки при х = х
0
),(),(
00
xfyyxfyy
′
=
′
=
′
== за формулою
Тейлора маємо:
.)()(
2
)(
2
0
2
0
0
xxoxx
xf
yy −+−
′′
=− Якщо б
,0)(
0
≠
′′
xf
різниця
yy − зберігала б знак у деякому околі точки х
0
, у той час, як у
точці перегину ця різниця повинна змінювати знак. Отже,
f′′(x
0
) = 0.
Теорема 8 (достатня умова точок перегину). Якщо функція
y = f(x) диференційована в точці х
0
, двічі диференційована у
проколеному околі цієї точки і f′′(x) змінює знак при х = х
0
, то
х
0
– точка перегину
Зауваження. Можна довести, що якщо в умовах теореми 5 кри-
тична точка не є точкою екстремуму, то вона є точкою перегину.
Приклад 2.16. Знайдемо інтервали опуклості й угнутості та точки
перегину функції
y = x³ – 6x² + x – 12.
► Для цього знайдемо другу похідну, прирівняємо її до нуля й
зробимо відповідний висновок:
y′ = 3x² – 12x + 1, y′′ = 6x – 12. y′′ = 0
при
х = 2, y′′ < 0 при х < 2, y′′ > 0 при х > 2.
Отже, графік функції є опуклим при
х < 2, вгнутим при х > 2, а
х = 2 – точка його перегину.
2.16.5. Асимптоти
Пряма називається асимптотою графіка функції y = f(x), якщо
відстань від змінної точки цього графіка до прямої наближається до
нуля при віддаленні точки у нескінченність.
Розглянемо
три види асимптот та визначимо способи їх знахо-
дження.
1.
Вертикальні асимптоти, що задаються рівняннями
х = а.
У цьому випадку означення асимптоти підтверджується, якщо
хоча б одна з односторонніх границь функції в точці
а нескінченна.
Приклад 2.17. Вертикальною асимптотою графіка функції y = 1 / x
є пряма х = 0, тобто вісь ординат.
2.
Горизонтальні асимптоти – прямі, задані рівняннями
у = а.
Такі асимптоти має графік функції, границя якої при
+∞→
x
або
при
−∞→
x
скінченна, тобто
.)(lim axf
x
=
±∞→

ДВНЗ “Українська академія банківської справи НБУ”
54
3.
Похилі асимптоти – прямі, що задаються рівняннями
y = kx + b.
Знайдемо k і b. Оскільки при
∞
→
x
,)( bk
x
x
f
+≈ то
,
)(
lim k
x
xf
x
=
∞→
якщо ця границя існує, скінченна й не дорівнює нулю.
Проте навіть при виконанні цих умов похила асимптота може не існу-
вати. Для її існування треба, щоб була скінченна границя при
∞
→
x
різниці
f(x) – kx. Ця границя дорівнюватиме b, оскільки при
∞
→
x
bk
x
x
f
≈−)(
.))((lim
bkxxf
x
=
−
∞→
Зауваження. Кількість вертикальних асимптот графіка функції
необмежена, а похилих і горизонтальних разом може бути не більше
двох (при
−∞→
x
и при ).
+
∞→
x
Приклад 2.18. Функція y = tgx має розриви 2-го роду при
nx
π
π
+=
2
, n ∈ Z, оскільки односторонні границі в цих точках нескін-
ченні. Отже,
nx
π
π
+=
2
, n ∈ Z – вертикальні асимптоти графіка.
Приклад 2.19. Функція
1
1
2
−
+
=
x
x
y
має нескінченний розрив при х = 1,
тобто
х = 1 – вертикальна асимптота. Границя функції на нескінчен-
ності:
,lim ∞=
∞→
y
x
тому горизонтальних асимптот графік не має. Переві-
римо наявність похилих асимптот. Для цього обчислимо
.1
)1(
1
lim
)(
lim
2
=
−
+
==
∞→∞→
xx
x
x
xf
k
xx
.1
1
1
lim
1
1
lim))((lim
2
=
−
+
=
⎟
⎠
⎞
⎜
⎝
⎛
−
−
+
=−=
→∞→∞→∞
x
x
x
x
x
kxxfb
xxx
Зауважимо, що обидві границі не залежать від знака нескінченно-
сті, тому пряма
y = x + 1 є асимптотою графіка на обох кінцях осі Ox.
2.16.6. Загальна схема дослідження функції
та побудови її графіка
Результати, отримані при вивченні різних аспектів поведінки
функції, дозволяють сформулювати загальну схему її дослідження з
метою побудови якісного графіка, що відображає характерні особли-
вості поведінки даної функції. Для цього необхідно визначити:
1)
ОДЗ функції та її поведінку на межах області визначення (знайти
відповідні односторонні границі або границі на нескінченності);

ДВНЗ “Українська академія банківської справи НБУ”
55
2)
парність і непарність функції;
3)
інтервали неперервності й точки розриву (вказати при цьому тип
розриву);
4)
нулі функції (тобто значення х, при яких f(x) = 0), й області постій-
ності знака;
5)
інтервали монотонності й екстремуми;
6)
інтервали опуклості та вгнутості й точки перегину;
7)
асимптоти графіка функції.
Зауважимо, що детальна відповідь на перше питання фактично
містить відповіді на друге та частково на сьоме питання. Дійсно, якщо
в область визначення не входять окремо розташовані точки й знайдені
односторонні границі функції в цих точках, то тим самим вказано ха-
рактер розривів. Зокрема, якщо деяка з цих односторонніх
границь не-
скінченна, через точку розриву (або через відповідну границю області
визначення) проходить вертикальна асимптота. Якщо область визна-
чення функції необмежена зліва або справа й на нескінченності відпо-
відного знака існує скінченна границя функції, то графік має на вказа-
ному кінці
Ох горизонтальну асимптоту.
Приклад 2.20. Дослідимо функцію
3
5
2
−
−
=
x
x
y
і побудуємо її графік.
► 1. Область визначення функції: ).;3()3;(
∞
+
∪
−
∞
∈
x
Поведінка на межах:
.
3
5
lim,
3
5
lim,
3
5
lim,
3
5
lim
22
03
2
03
2
+∞=
−
−
+∞=
−
−
−∞=
−
−
−∞=
−
−
+∞→+→−→−∞→
x
x
x
x
x
x
x
x
xxxx
2. ),()(
x
f
x
f
±
≠− отже, функція не є парною або непарною,
тобто маємо функцію загального вигляду.
3. Оскільки функція є елементарною, вона неперервна на всій
області визначення, тобто проміжки неперервності ).;3()3;(
∞+∪
−
∞
∈
x
Із відповіді на перше запитання випливає, що
х = 3 – точка розриву
2-го роду.
4. Рівняння ,0)(
=
x
f
тобто 0
3
5
2
=
−
−
x
x
має два корені
.5±=x
Отже, графік функції перетинає вісь
Ох у точках
5
1
−=x
,
.5
2
=x
5. Знайдемо похідну даної функції:
.
)3(
)1)(5(
2
−
−
−
=
′
x
xx
y
0=
′
y
при
,5=
x
.1=
x
Дослідимо знак похідної:
0)( <
′
xf
при
)5;3()3;1(
∪∈
x
– інтервали спадання функції; 0)( >
′
xf при
);5()1;(
∞+∪−∞∈
x
– інтервали зростання функції. При переході через
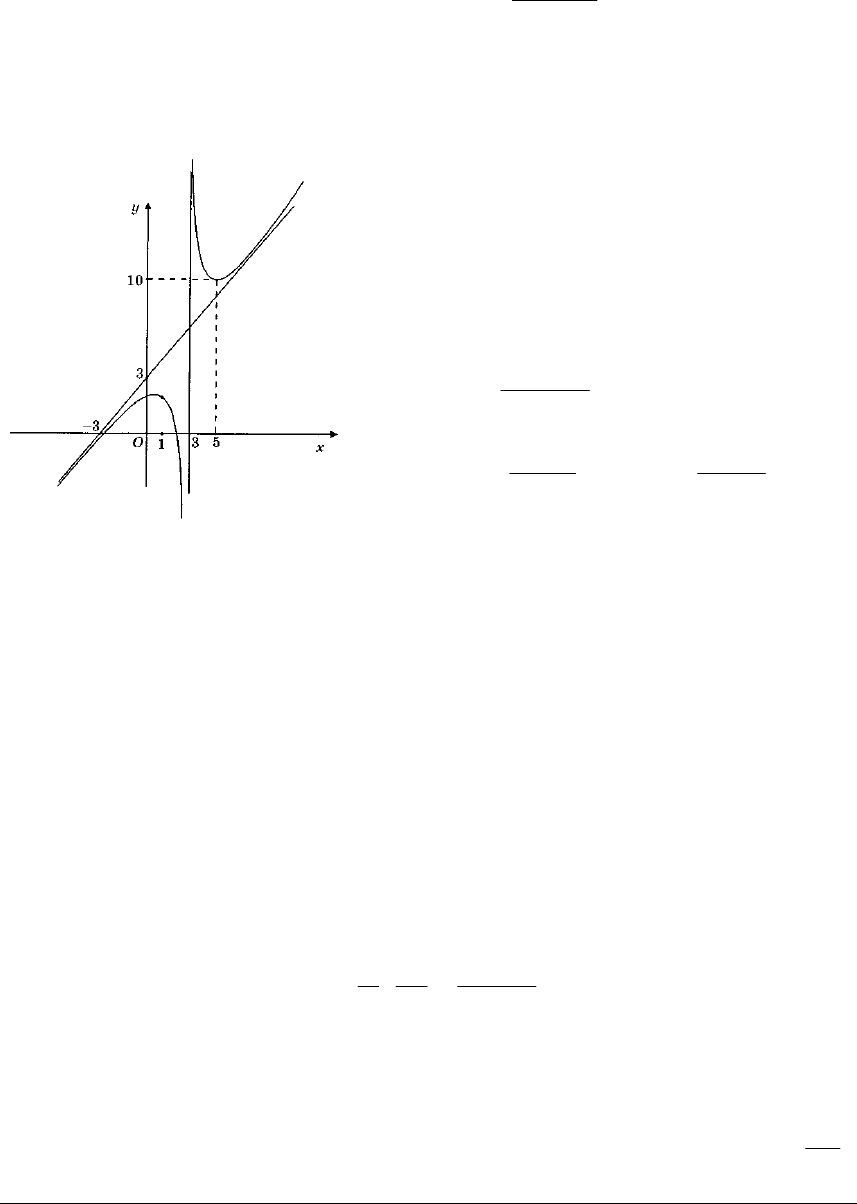
ДВНЗ “Українська академія банківської справи НБУ”
56
точку 1
=
x
)(xf
′
змінює знак з “+” на “–”, отже, 1
=
x
– точка макси-
муму, .2)1(
=
f
При переході через точку 5
=
x
)(xf
′
змінює знак з “–”
на “+”, отже, 5
=
x
– точка мінімуму, .10)5(
=
f
6. Знайдемо другу похідну:
.
)3(
8
3
−
=
′′
x
y
Оскільки рівняння
0
=
′′
y коренів не має, отже, функція не має точок перегину. 0)(
<
′′
xf
при
х < 3,
0)( >
′
′
xf
при x > 3, тому на інтервалі )3;(
−
∞ функція опу-
кла, а на інтервалі );3(
∞
+ – угнута.
Рис. 2.7
7. При відповіді на перше питання
показано, що
х = 3 – вертикальна аси-
мптота графіка функції, при
∞
→
х
функція не має скінченної границі, от-
же, не має й горизонтальних асимптот.
Знайдемо похилу асимптоту :
bk
x
y
+
=
.3
3
53
lim)
3
5
(lim
,1
)3(
5
lim
2
2
=
−
−
=−
−
−
=
=
−
−
=
±∞→±∞→
±∞→
x
x
x
x
x
b
xx
x
k
xx
x
Отже, 3+=
x
y – похила асимптота. Графік функції накреслено
на рис. 2.7.
2.17. ЗАСТОСУВАННЯ ПОХІДНОЇ В ЕКОНОМІЦІ.
ЕЛАСТИЧНІСТЬ ПОПИТУ
Ознайомимось з поняттям еластичності та деякими її застосуван-
нями.
Позначимо за p – вартість одного виробу, а x – кількість виробів,
що виготовлено й реалізовано за деякий інтервал часу: ).(
p
f
x
=
Еластичність попиту позначають літерою
η
, що називають
“ета”, і визначають так:
.
)(
)(
pf
pfp
dp
dx
x
p
′
=⋅=
η
Дамо пояснення еластичності попиту
η
. Якщо вартість виробу
зростає з p до ,
p
p
Δ+ тоді і кількість виробів також зміниться на ве-
личину ).()(
p
f
p
p
f
x
−Δ+=Δ Відносний приріст вартості буде
,
p
p
Δ

ДВНЗ “Українська академія банківської справи НБУ”
57
а відносний приріст функції попиту буде
.
x
x
Δ
Якщо відносний приріст
помножити на 100 %, то одержимо відповідний відсоток зміни почат-
кової вартості та початкового попиту. Якщо зростання вартості p ви-
кликає спад попиту, тоді .0<Δ
x
Розглянемо відношення відносного приросту попиту до відносно-
го приросту вартості одиниці продукції
.:
px
xp
p
p
x
x
Δ
Δ
=
Δ
Δ
Це співвідношення показує, у скільки разів відносний приріст
попиту більше відносного приросту вартості кожного виробу.
Якщо в останній рівності перейти до границі при ,0→
Δ
p
то оде-
ржимо:
.lim
0
px
xp
dp
dx
x
p
p
Δ
Δ
=⋅=
→Δ
η
Оскільки границя
η
відрізняється від виразу
px
xp
Δ
Δ
на нескінченно
малу більшого порядку малості відносно ,0→
Δ
p
то
.
px
xp
Δ
Δ
≈
η
Якщо:
•
відсоток зміни попиту більше відсотка зміни вартості ( 1−<
η
), тоді
попит називають еластичним;
•
відсоток зміни попиту менше відсотка зміни вартості ),01( <<−
η
тоді попит називають нееластичним;
•
,1−=
η
то попит називають адекватним вартості одиниці виробу.
Поняття еластичності можна застосовувати і до інших функцій
економічного змісту.
У загальному вигляді, якщо існує похідна функції )(
x
f
y = , тоді
існує границя
),(lim)(lim):(lim
00
xf
y
x
dx
dy
y
x
x
y
y
x
x
y
y
x
x
x
y
y
xxox
′
⋅=⋅=
Δ
Δ
=
Δ
Δ
⋅=
ΔΔ
→Δ→Δ→Δ

ДВНЗ “Українська академія банківської справи НБУ”
58
яку називають еластичністю функції )(
x
f
y
=
відносно змінної x і по-
значають :)( yE
x
.)(
dx
dy
y
x
yE
x
⋅=
(2.45)
Отже, еластичність є наближеним відсотком приросту функції
(зростання або спадання), що відповідає приросту незалежної змінної
на один відсоток.
Приклад 2.21. Встановимо зв’язок між доходом підприємства та
еластичністю попиту.
► Функція доходу підприємства
,)(
p
x
x
D
⋅
=
де x – кількість виготовлених та реалізованих виробів;
p – вартість кожного виробу.
Маргінальний дохід відносно вартості буде
).1()1()(
)(
η
+=⋅+=⋅+=⋅= x
dp
dx
x
p
x
dp
dx
pxpx
dp
d
dp
xdD
Якщо:
•
попит еластичний, то ,1
−
<
η
тому 01
<
+
η
і з формули (2.45) ви-
пливає, що
,0<
dp
dD
тобто дохід D, який розглядають як функцію
вартості від p, спадає;
•
попит нееластичний, то ,01
<
<
−
η
тоді 01 >
+
η
і
,0>
dp
dD
отже, у
цьому випадку дохід D зростає;
•
попит адекватний вартості, то ,1
−
=
η
01
=
+
η
і ,0=
dp
dD
тобто до-
хід не змінюється.
Питання для самоперевірки
1. Що називається похідною?
2.
Як формулюється геометричний, механічний та економічний зміст
похідної?
3.
Який вигляд має рівняння дотичної до графіка функції?
4.
Що означає диференційованість функції?
5.
Що називається диференціалом?
6.
Як формулюється геометричний зміст диференціалу?
7.
Яка операція називається лінеаризацією функції?

ДВНЗ “Українська академія банківської справи НБУ”
59
8.
Як формулюються правила диференціювання? Чому дорівнює по-
хідна складеної функції, похідна оберненої функції?
9.
Як формулюється властивість інваріантності диференціала?
10.
Який вигляд має таблиця похідних?
11.
У чому полягає метод логарифмічного диференціювання, і коли
він використовується?
12.
Який вигляд має формула похідної функції, що задана парамет-
рично?
13.
Що називається похідною n-го порядку?
14.
Які властивості похідних вищого порядку?
15.
Що називається диференціалом n-го порядку?
16.
Які властивості диференціалів вищого порядку?
17.
Які точки називаються точками екстремуму?
18.
Як формулюються основні теореми диференціального числення?
19.
Як формулюється правило Лопіталя?
20.
Яка формула називається формулою Тейлора?
21.
Що називається залишковим членом формули Тейлора?
22.
Які існують форми залишкового члена у формулі Тейлора?
23.
Як розкладають основні елементарні функції в ряд Тейлора?
24.
Яка функція називається зростаючою (спадною) на деякому про-
міжку?
25.
Як формулюються необхідна та достатня умови екстремуму?
26.
Як знайти найбільше та найменше значення диференційованої фу-
нкції на відрізку?
27.
Яка крива називається опуклою (вгнутою) в деякій точці, на де-
якому проміжку?
28.
Яка точка називається точкою перегину?
29.
Як формулюються необхідна, достатня умови точок перегину?
30.
Що називається асимптотою?
31.
Які види асимптот, якими рівняннями вони задаються?
32.
Які етапи входять до складу схеми дослідження функції?
33.
Які приклади застосування похідної в економіці?
34.
Що називається еластичністю функції?
35.
Коли попит називають еластичним, нееластичним, адекватним ва-
ртості одиниці виробу?
ДВНЗ “Українська академія банківської справи НБУ”
60
3. ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ
3.1. ПОНЯТТЯ ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ
Впорядкований набір з n дійсних чисел
n
xxx ,,,
21
… позначається
),,,(
21 n
xxxM … і називається точкою n-вимірного простору ;
n
R
самі числа
n
xxx ,,,
21
… називаються координатами точки
).,,,(
21 n
xxxMM …=
Нехай
n
RD ⊆ – довільна множина точок n-вимірного простору.
Якщо кожній точці
DxxxM
n
∈
),,,(
21
…
поставлено у відповідність де-
яке дійсне число ),,,,()(
21 n
xxxfMf …
=
то кажуть, що на множині D
визначена числова функція від n змінних .,,,
21 n
xxx … Множина D на-
зивається областю визначення функції ).(
M
f
У частинному випадку, коли n = 2, функція двох змінних
),( y
x
f
z = може розглядатися як функція точок площини
x
O
y
у три-
вимірному просторі з фіксованою декартовою системою координат.
Графіком цієї функції називається множина точок простору
{
}
,),(:),,(
3
yxfzRzyxΓ =
∈
= що являє собою деяку поверхню в .
3
R
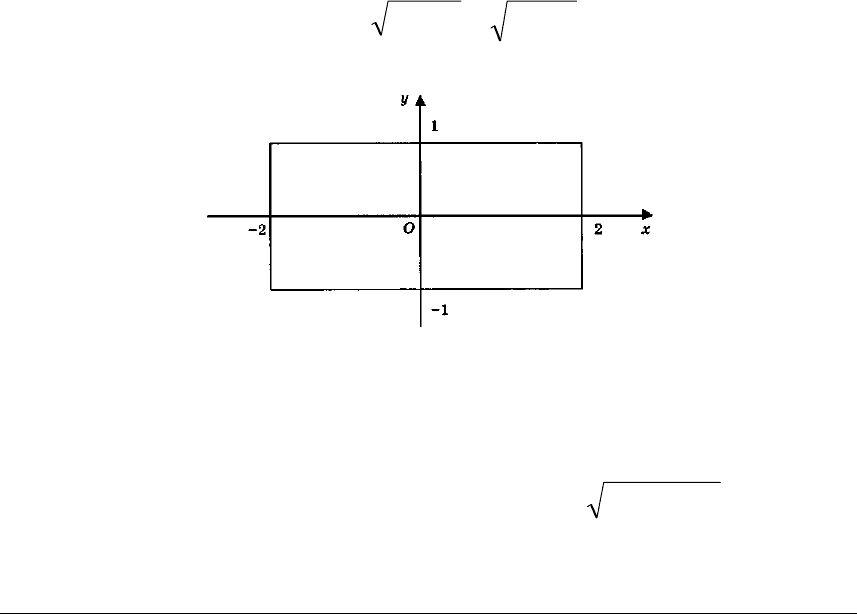
Приклад 3.1. Визначити область визначення функції
.14
22
yxz −+−=
► Шуканою областю буде прямокутник (рис. 3.1):
Рис. 3.1
Справді, з нерівностей 01,04
22
≥
−
≥
−
yx маємо 1,4
22
≤
≤ yx
або ,22 ≤≤−
x
.11 ≤≤− y
Приклад 3.2. Накреслити графік функції .1
22
yxz −−=
► Графіком цієї функції є півсфера з радіусом 1, розміщена над
площиною
x
O
y
(рис. 3.2).
