Долгіх В.М. Математика для економістів - Математичний аналіз. Диференціальне числення

Подождите немного. Документ загружается.

ДВНЗ “Українська академія банківської справи НБУ”

Наслідок. Диференціал функції можна записати так:

,)( dxxfdy

′

(2.4)

а похідну – у вигляді

.)(

xf =

′

Теорема 2. Якщо функція диференційована в деякій точці, то

вона неперервна в цій точці

Z Із формули (2.3) випливає:

,0lim

→Δ

що й означає непере-

рвність f(x) при х = х

. 

Зауваження. Обернене твердження хибне, тобто з неперервності

функції не випливає її диференційованість.

Наприклад, y = |x| неперервна але недиференційована в точці

х = 0.

2.2.2. Геометричний зміст диференціала

Для з’ясування геометричного змісту диференціала знову звер-

немося до рис. 2.1. У трикутнику

KNM

.)(tg

dyxxfKMNK

⋅

′

⋅

Отже, геометричний зміст диференціалу: диференціал функції

дорівнює приросту ординати дотичної до графіка функції y = f(x) у

точці х

2.3. ЛІНЕАРИЗАЦІЯ ФУНКЦІЇ

Оскільки справжнє значення приросту функції відрізняється від її

диференціала на нескінченно малу величину більш високого порядку,

ніж Δх, при наближених обчисленнях можна Δу заміняти на dy, тобто

вважати, що:

f(x

+Δx) ≈ f(x

) + dy = f(x

) + f '(x

)(x – x

При цьому для значень х, близьких до х

, функція f(x) наближено

заміняється на лінійну функцію. Ця операція називається лінеаризацією

функції.

Приклад 2.1. Знайдемо наближене значення

.02,1

► Покладемо

.02,0,1,)(

=Δ== xxxxf Тоді

.01,101,0102,0

102,0)1()1()02,01( =+=⋅+=⋅

′

+≈+ fff



ДВНЗ “Українська академія банківської справи НБУ”

2.4. ПРАВИЛА ДИФЕРЕНЦІЮВАННЯ

Припустимо, що функції f(x) й g(x) диференційовані. Доведемо де-

які властивості похідних, які називають правилами диференціювання.

1. Похідна від суми дорівнює сумі похідних:

).()())()(( xgxfxgxf

′

+ (2.5)

Δ+Δ

−

′

→Δ→Δ

gfggff

xgxf

xx 00

lim

)()(

lim))()((

.)(lim

′

→Δ



2. Сталий множник можна виносити за знак похідної:

),())(( xfkxkf

′

(k = const). (2.6)

Z ).(limlim

)(

lim))((

000

xfk

kfkfkf

xkf

xxx

′

−

′

→Δ→Δ→Δ



3. Похідна від добутку:

).()()()())()(( xgxfxgxfxgxf

′

⋅

(2.7)

ΔΔ+Δ+

−

′

⋅

→Δ→Δ

gfgffg

fgggff

xgxf

xx 00

lim

))((

lim))()((

,lim

gfgfg

′

⎟

⎠

⎞

⎜

⎝

⎛

→Δ

оскільки

0lim

=Δ

→Δ

через неперервність g(x). 

4. Якщо g(x) ≠ 0, то

)(

)()()()(

)(

xgxfxgxf

′

−

′

⎟

⎠

⎞

⎜

⎝

⎛

(2.8)

Z =

Δ+⋅Δ

−Δ−Δ+

⎟

⎠

⎞

⎜

⎝

⎛

−

Δ+

′

⎟

⎠

⎞

⎜

⎝

⎛

→Δ→Δ

)(

lim

)(

gggx

fggffgfg

xxg

)(

lim

gfgf

ggg

′

−

′

Δ+

−

→Δ

. 

ДВНЗ “Українська академія банківської справи НБУ”

2.5. ПОХІДНА СКЛАДЕНОЇ ФУНКЦІЇ

Теорема.

Якщо функція u = φ(x) має при деякому значенні х

похідну u

' = φ'(x), а функція y = f(u) має при відповідному зна-

ченні u похідну y

' = f'(u), то складена функція y = f(φ(x)) має

похідну по х, що дорівнює

y'(x) = f'(u)u'(x) (2.9)

Z Оскільки ),(lim uy

′

→Δ

то: ,)(

′

де 0→

при

.0→Δu Тоді

⇒

⋅

+Δ

′

=Δ uuuyy

)(

.)(

′

Перейдемо до границі при Δх → 0 з урахуванням

:0lim

→Δ

).()()( xuufxy

′



2.6. ПОХІДНА ОБЕРНЕНОЇ ФУНКЦІЇ

Якщо для функції y = f(x) існує обернена функція х = φ(у), яка в

точці у має похідну φ′(у) ≠ 0, то у відповідній точці х функція f(x) та-

кож має похідну:

)(

′

(2.10)

Z Можна подати

Оскільки х = φ(у) неперервна, то

Δх → 0 при Δу → 0, тому при переході до границі при Δу → 0, отри-

маємо:

)(

yyx

′



2.7. ІНВАРІАНТНІСТЬ ФОРМИ

ДИФЕРЕНЦІАЛА ПЕРШОГО ПОРЯДКУ

Знайдемо вираз для диференціала складної функції y = f(φ(x)), де

y = f(u), u = φ(x). Похідна функції

),()( xuf

′′

отже,

.)()( dxxufdy

′′

Але

,)( dudxx

′

тому

.)( duufdy

′

(2.11)

ДВНЗ “Українська академія банківської справи НБУ”

Таким чином, форма диференціала першого порядку не зале-

жить від того, чи є аргумент функції незалежною змінною чи функ-

цією іншого аргументу. Ця властивість називається властивістю

незмінності або інваріантності диференціала.

2.8. ПОХІДНІ ОСНОВНИХ ЕЛЕМЕНТАРНИХ ФУНКЦІЙ

Знайдемо похідні основних елементарних функцій:

Якщо f(x) = C = const, то ΔС= 0, тому С'= 0.

y = sinx,

.cos

)

cos(

sin

lim

sin)sin(

lim

xxx

−Δ+

′

→Δ→Δ

y = cosx,

.sin)

sin(

sin

lim

cos)cos(

lim

xxx

−=

−Δ+

′

→Δ→Δ

cos

cossin

cos

scosincosnsi

cos

sin

)tg(

xxxx

x =

′

−

′

⎟

⎠

⎞

⎜

⎝

⎛

′

Аналогічно можна отримати формулу .

sin

)ctg(

x −=

′

.ln

limlim)(

xxx

−

′

→Δ

Δ+

→Δ

)1ln(

lim

ln)ln(

lim)(ln

xxx

−Δ+

′

→Δ→Δ

()

.ch

)(

sh x

eeeeee

xxxxxx

−−

′

⎟

⎠

⎞

⎜

⎝

⎛

−

′

−−−

Аналогічно можна знайти похідні інших гіперболічних функцій.

За формулою похідної оберненої функції:

а)

;

sin1

cos

)(sin

)(arcsin

−

′

б)

;

0)arcsin

()(arccos

−

−=

−

−=

′

−=

′

в)

;

tg1

cos

)tg(

)arctg(

′

г)

)arctg

()arcctg(

−=

′

−=

′

ДВНЗ “Українська академія банківської справи НБУ”

10.

Якщо α – довільне дійсне число, то

)ln()()(

1lnln −

=⋅⋅=

′

ααααα

ααα

xxeex

У результаті маємо таблицю похідних основних елементарних

функцій:

1. .0)( =

′

2. .)(

1−

′

αα

.)(;ln)(

xxxx

eeaaa =

′

)(ln;

)(log

′

5. .cos)(sin xx =

′

6. .sin)(cos xx

−

′

cos

)tg(

x =

′

sin

)ctg(

x −=

′

.ch)sh( xx =

′

10.

.sh)ch( xx

′

11.

)th(

x =

′

12. .

)cth(

x =

′

13.

.1,

)(arcsin

−

′

14.

.1,

)(arccos

−

−=

′

15.

)arctg(

′

16.

)arcctg(

−=

′

2.9. ЛОГАРИФМІЧНЕ ДИФЕРЕНЦІЮВАННЯ

Іноді корисно використовувати формулу так званого логарифміч-

ного диференціювання.

Припустимо, що f(x) > 0 на деякій множині значень аргументу і

диференційована на цій множині. Тоді за формулою похідної складе-

ної функції:

),(

)(

))((ln xf

′

⋅=

′

звідки .))((ln)()(

′

⋅

′

xfxfxf (2.12)

Цією формулою користуються для обчислення похідних степенево-

показникових функцій u(x)

v(x)

, а також похідних громіздких добутків

та часток.

Приклад 2.2. Знайдемо похідну степенево-показникової функції

xy =

► За допомогою формули логарифмічного диференціювання:

).1(ln)

(ln)ln()(ln)( +=+=

′

xxxxxxxxx

xxxxxx



ДВНЗ “Українська академія банківської справи НБУ”

Приклад 2.3. Знайдемо похідну функції

sin)14(

73)52(

⎟

⎠

⎞

⎜

⎝

⎛

−

−+

► Користуючись властивостями логарифма та формулою (2.12):

−

−+

′

⎟

⎠

⎞

⎜

⎝

⎛

−

−+

sin)14(

73)52(

sin)14(

73)52(

()

′

−−−−++× )sinln7)14ln(8)73ln(

52ln(7 xxxx

.ctg7

)73(5

sin)14(

73)52(

⎟

⎠

⎞

⎜

⎝

⎛

−

+−

−+

xxxxx



2.10. ДИФЕРЕНЦІЮВАННЯ ФУНКЦІЙ,

ЗАДАНИХ ПАРАМЕТРИЧНО

Якщо функція y = f(x) задана параметрично:

⎩

⎨

⎧

)(

, де функ-

ція φ(t) має обернену функцію t = Φ(x), тоді у = ψ(Φ(х)), і

)(

)()()()(

txΦtxy

′

′′

′

ψψ

. (2.13)

Отримана формула дає можливість знаходити похідну функції, що

задана параметрично, без визначення безпосередньої залежності у від х.

Приклад 2.4

⎩

⎨

⎧

−=

−

)cos1(

)sin(

tax

ttay

– параметричні рівняння кривої, що називається

циклоїдою. Знайдемо у'(х).

► у'(t) = asint, х'(t) = a(1 – cost). Отже, за формулою (2.13):

cos1

sin

)cos1(

sin

)(

−

′



2.11. ПОХІДНІ ТА ДИФЕРЕНЦІАЛИ ВИЩИХ ПОРЯДКІВ

2.11.1. Похідні вищих порядків, їх властивості

Припустимо, що функція y = f(x) диференційована на відрізку

[a, b]. Її похідна також є функцією від х. Похідна від неї називається

похідною другого порядку функції f(x). Продовжуючи виконувати цю

операцію, можна отримати похідні третього, четвертого й більш високих

порядків. При цьому f '(х) називатимемо похідною першого порядку.

Похідною n-

го порядку (n-ю похідною) від функції f(x) називаєть-

ся похідна (першого порядку) від її (n – 1)-ї похідної:

(n)

=(y

(n – 1)

)'= f

(n)

(x).

ДВНЗ “Українська академія банківської справи НБУ”

Приклад 2.5. Знайдемо похідну 3-го порядку функції

y = x³ – 5x² + 3x + 12.

► y' = 3x² – 10x + 3, y'' = (y')' = 6x – 10, y''' = (y'')' = 6.



Приклад 2.6. Отримаємо загальну формулу для похідної n-го по-

рядку функції y = a

► y' = а

·lna · b, y'' = lna · b(a

)' = a

·ln²a · b², …, y

(n)

= a

· ln

a · b

. 

Властивості похідних вищих порядків

Основні властивості похідних вищих порядків випливають із від-

повідних властивостей першої похідної:

(cf(x))

(n)

= c · f

(n)

(x) (с = const).

(f(x) + g(x))

(n)

= f

(n)

(x) + g

(n)

(x).

Для y = x

: y

(n)

= n(n – 1)…(n – m + 1)x

m – n

. Якщо m – натуральне чи-

сло, то при n > m y

(n)

= 0.

Похідна n-го порядку від добутку функцій f(x)g(x) обчислюється за

формулою Лейбніца:

()

....

)1(

)()2()1()(

)(

nnnn

fggf

gnfgffg ++

′′

⋅

−

′

−−

(2.14)

Коефіцієнти в цій формулі співпадають із відповідними коефіціє-

нтами формули бінома Ньютона, якщо замінити похідні даного по-

рядку тим же степенем змінної. Для n = 1 ця формула була отримана

при вивченні першої похідної, для похідних вищих порядків її можна

довести за допомогою методу математичної індукції.

Виведемо формулу для другої похідної функції, що задана параме-

тричними рівняннями: x = φ(t), y = ψ(t), t

≤ t ≤ T.

Перша похідна

Отже,

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

(2.15)

2.11.2. Диференціали вищих порядків, їх властивості

Диференціал від диференціала функції називається її другим ди-

ференціалом, або диференціалом другого порядку, та позначається

d²y = d(dy).

ДВНЗ “Українська академія банківської справи НБУ”

При обчисленні другого диференціала врахуємо, що dx не зале-

жить від х, та при диференціюванні виноситься за знак похідної як

сталий множник. Отже,

²y = d(dy) = d(f '(x)dx) = (f '(x)dx)'dx = (f '(x))'(dx)² = f ''(x)dx². (2.16)

Аналогічно можна знайти третій диференціал:

³y = d(d ²y) = f '''(x)dx³,

а також диференціали більш високих порядків.

Диференціалом n-го порядку називається перший диференціал від

диференціала (n – 1)-го порядку:

y = d(d

n – 1

y) = f

(n)

(x)dx

. (2.17)

Властивості диференціалів вищих порядків

1. Якщо х – незалежна змінна, то похідну будь-якого порядку

можна подати як відношення диференціалів відповідного порядку:

,)(

xf =

′

.)(...,,)(

)(

xf ==

′′

(2.18)

Диференціали вищих порядків не мають властивості інваріант-

ності.

Z Покажемо це на прикладі другого диференціала. Якщо

y = F(φ(x)) = F(u), де u = φ(x), то d

²y = d(F'(u)du). Але du = φ'(x)dx за-

лежить від х, тому d²y = d(F'(u))du + F

'(u)d(du) = F''

(u)(du)² +

+ F

'(u)d ²u, де d ²u = φ''(x)(dx)².

Отже, форма другого диференціала змінилась при переході до ар-

гументу u.



2.12. ТОЧКИ ЕКСТРЕМУМУ ФУНКЦІЇ.

ОСНОВНІ ТЕОРЕМИ ДИФЕРЕНЦІАЛЬНОГО ЧИСЛЕННЯ

2.12.1. Точки екстремуму функції

Точка х

називається точкою максимуму (мінімуму) функції y = f(x),

якщо f(x) ≤ f(x

) (f(x) ≥ f(x

)) для всіх х із деякого δ-околу точки х

Точки максимуму та мінімуму функції називаються точками ек-

стремуму.

Приклади

1. y = x² має мінімум при х = 0.

y = –|x – 3| має максимум при х = 3.

у = sinx має мінімуми при

+−=

і максимуми при

n ∈

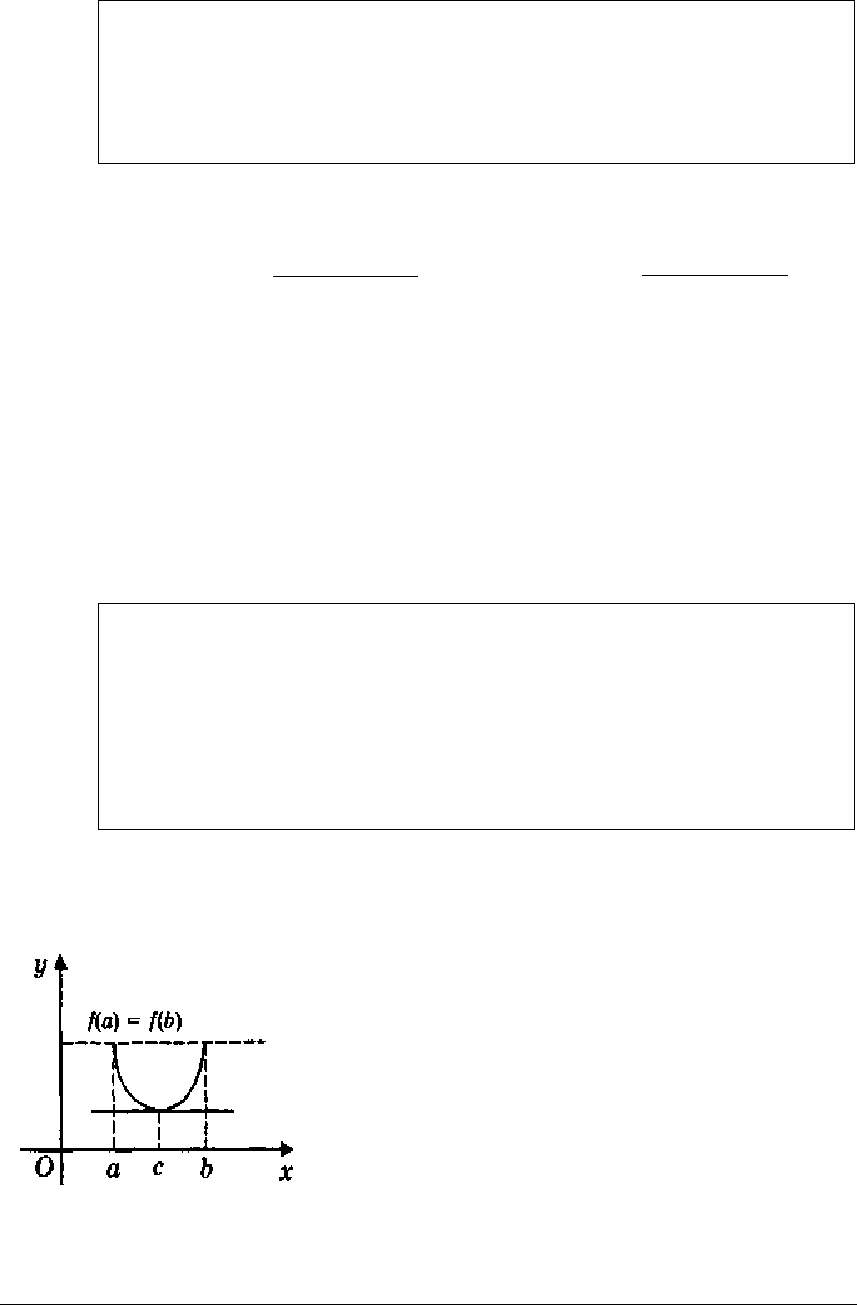
ДВНЗ “Українська академія банківської справи НБУ”

2.12.2. Теорема Ферма

Теорема 1 (теорема Ферма). Якщо функція y = f(x) визначена

в деякому околі точки х

, приймає в цій точці найбільше

(найменше) значення з околу, що розглядається і має в точці х

похідну, то

f ′(x

) = 0 (2.19)

Z Припустимо, що f(x

) – найбільше значення функції, тобто для

будь-якої точки обраного околу виконується нерівність f(x) ≤ f(x

Тоді, якщо x < x

)()(

≥

−

xfxf

а якщо x > x

, .0

)()(

≤

−

xfxf

Перейдемо до границі в отриманих нерівностях, знайдемо, що з

першої нерівності випливає, що f ′(x

) ≥ 0, а з другої – f ′(x

) ≤ 0. Отже,

f ′(x

) = 0. 

Зауваження. У теоремі Ферма важливо, що х

– внутрішня точка

для даного проміжку. Наприклад, функція y = x, що розглядається на

[0; 1], набуває найбільшого та найменшого значень при х = 1 та х = 0,

але її похідна в цих точках у нуль не обертається.

2.12.3. Теорема Ролля

Теорема 2 (теорема Ролля). Якщо функція y = f(x):

1) неперервна на відрізку [a, b];

2) диференційована в усіх внутрішніх точках цього відрізку;

3) набуває рівних значень на кінцях цього відрізка, тобто

f(a) = f(b), то всередині інтервалу (a, b) існує хоча б одна

точка х = с, a < c < b така, що

f ′(c) = 0 (2.20)

Z Припустимо, що M і m – найбільше та найменше значення f(x)

на [a, b]. Тоді, якщо m = M, то f(x) = m = M – стала функція, і f ′(x) = 0

для будь-якої точки відрізку [a, b].

Рис. 2.2

Якщо ж m < M, то за теоремою

Вейєрштрасса хоча б одне із значень m

або M досягається у внутрішній точці с

відрізка [a, b] (оскільки на кінцях відріз-

ка функція набуває рівних значень). Тоді

за теоремою Ферма f ′(c) = 0.



Геометричний зміст теореми Ролля.

Серед усіх дотичних до графіка функції

y = f(x) знайдеться принаймні одна, пара-

лельна осі Ox.

ДВНЗ “Українська академія банківської справи НБУ”

2.12.4. Теорема Лагранжа

Теорема 3 (теорема Лагранжа). Якщо функція y = f(x) непе-

рервна на відрізку [a, b] і диференційована в усіх внутрішніх

точках цього відрізку, то всередині відрізка [a, b] знайдеться

хоча б одна точка c, a < c < b, що

f(b) – f(a) = f ′(c) (b – a) (2.21)

Z Позначимо за

afbf

−

)()(

і розглянемо допоміжну функцію

F(x) = f(x) – f(a) – (x – a)Q.

Ця функція задовольняє усі умови теореми Ролля: вона непере-

рвна на [a, b], диференційована на (a, b) і F(a) = F(b) = 0. Отже, на ін-

тервалі (a, b) існує точка с, у якій

F′(c) = 0. Але F′(x) = f ′(x) – Q, тобто

F′(c) = f ′(c) – Q = 0, звідки

Рис. 2.3

).(

)()(

afbf

′

−



Геометричний зміст теоре-

ми Лагранжа: серед усіх дотич-

них до графіка функції y = f(x)

знайдеться принаймні одна, пара-

лельна січній АВ (рис. 2.3).

2.12.5. Теорема Коші

Теорема 4 (теорема Коші). Якщо f(x) і g(x) – функції, що не-

перервні на [a, b], диференційовані на (a, b), і g′(x) ≠ 0 на (a, b),

то знайдеться така точка x = c, (a < c < b), що

)(

)()(

agbg

afbf

′

−

(2.22)

Z Позначимо через

)()(

agbg

afbf

−

При цьому g(b) – g(a) ≠ 0,

інакше за теоремою Ролля знайшлась б точка всередині відрізка [a, b],

в якій g′(x) = 0, що суперечить умові теореми. Розглянемо допоміжну

функцію F(x) = f(x) – f(a) – Q(g(x) – g(a)), для якої виконуються усі

умови теореми Ролля. Як наслідок,

всередині відрізка [a, b] існує точка

х = с, в якій F′(c) = 0. Але F′(x) = f ′(x) – Qg′(x), тому f ′(c) – Qg′(c) = 0,

звідки

)(

′

. Підставляючи в цю рівність значення Q, отримаємо

формулу (2.22).

