Doktorov E.V., Leble S.B. A Dressing Method in Mathematical Physics

Подождите немного. Документ загружается.

6.4 Dressing in multicenter problem 179

multichannel problem, but to composite particles as well [406]. The matrix

is a pr ojection of a complicated basis tha t includes the orbital momenta; the

only possible place for them to exist is the potential, if we restrict ourselves

to the one-particle case. We will see in the next section that the DT-bas ed

approach provides a constructive method to describe general multiparticle

systems, which is especially important in the multicenter problem.

6.4 Dressing in multicenter problem

The results of the previous section allow us to build a ZRP eigenfunction in

the multicenter problem. In a more general situation we can also consider a

system with a smooth potential plus a number of ZRP s. If the Gr een function

for the smooth potential is known, we can provide a solution for the problem

with the ZRPs added. This procedure was outlined in [115], where the case

of a single ZRP was considered. Generalization to an arbitrary number of

ZRPs is straightforward. In contrast, our general idea is to dress a multicenter

system without using the Green function. This method gives simple formulas

for partial phases and their corrections at low energies [284].

Let us consider a scattering problem for a nonspherical potential



−

∂

∂r

−

∂

∂r

U − E



ψ(r)=0, (6.50)

where

is square of the angular momentum operator and E is the energy of

a particle. The asymptotic of wave function ψ(r) looks like

ψ(r)

r→∞

∼ exp(ik · r)+f(θ)

ikr

, (6.51)

where f(θ) is the scattering amplitude which depends on scattering angle θ.

The operator

commutes with all radial derivatives, in particular with

∂ = ∂/∂r. In the three-dimensional space the DT can be reduced to the

one-dimensional Heisenberg matrix (or operator) problem (6.30) with appro-

priately chosen variable x and with a basis of (orthogonal) functions of the

rest variables. In our case x = r, functions a

and a

are the same as in (6.36)

and

The radial DT for any solution of the Schr¨odinger equation is similar to that

obtained in Sect. 6.1, but s should be treated as a function of the operator

variable

. The transformation of the potential is written as

U →

(1)

U +

− s

′

. (6.52)

180 6 Applications of dressing to linear problems

In order to ﬁnd the operator s, we use the covariance principle for (6.50). The

covariance principle (6.32) formally yields an explicit constraint for s which

looks like

′

+[a

,s]+(a

′

+[a

,s]s + {a

′

+ s

)}

′

+[a

,s](s

′

+ s

)

= a

′

+(a

′

+ {a

′

+ s

)}

′

=0.

Integrating over r, we obtain the operator equation for s whichinourcase

can be written as

′

s + s

U + C(

). (6.53)

The integration “constant” C(

) is a function of the operator variable

which does not depend on r [289]. The sense of this “constant” can be

understood from the asymptotic behavior of s at inﬁnity r →∞, where (6.53)

go es to

′

+ s

= C(

The general solution of this (Riccati) equation for the asymptotic in r at

inﬁnity gives either oscillations or s(∞)=K(

), then C(

)=K(

)

The operator s may be found as a series



∞

n=0

, where coeﬃcients

depend only on r. It is easy to show that (6.53) leads to the recursion

relations for the coeﬃcients s

′

+ s

U + C(0),

′

+ s

+ C

′

(0),

′



k=0

n−k

= C

(n)

(0),n≥ 2.

For example, the ﬁrst equatio n in the region where U = 0 looks like

′

+ s

= K

where K

is the zeroth coeﬃcient in the expansion K =



∞

n=0

.Equa-

tion (6.52) gives a nonlocal (with respect to angles) potential which depends

. Thus, we have the algorithm that determines the operator s and the

dressed potential via the operator K. To evaluate the cross section, we need

only partial phases or a scattering amplitude related to the operator K.In

order to ﬁnd the partial phases for the dressed potential, we should apply

the DT to the wave function. However, a problem occurs: the DT in general

modiﬁes the plane wave exp(ik · r). Thus, the DT applied to wave function

ψ(r) with the asymptotic (6.51) gives another asymptotic. In some particular

6.5 Applications to X

and YX

structures 181

cases, sp ecial choice of the operator K allows us to avoid such a problem. We

consider this choice as a condition in the formulation of a scattering problem.

Indeed, consider the partial wave asymptotic for a nonspherical poten-

tial [48]

(r) ∼

2ikr



ikr+iδ

(n) − e

−ikr−iδ

(−n)



, (6.54)

where n is the unit vector directed as r, δ

denotes partial shifts, and Λ

(n)

are normalized eigenvectors of the S matrix operator (partial harmonics). The

simplest formulas for the shifts δ

(1)

for the potential

(1)

result when partial

harmonics Λ

are also eigenvectors of the op erator K. For example, suppose

all partial harmonics Λ

are eigenvectors of K but only Λ

has nonzero eigen-

value κ,

KΛ

(n)=κΛ

(n).

The asymptotic dressing is reduced to the action of the operator ∂ − K on

asymptotic (6.54). It is easy to show by using the expression



κ − ik

κ +ik



= −2i arctan(k/κ)

for real-valued variables k and κ that the DT changes only the partial shift δ

(1)

= δ

− arctan(k/κ). (6.55)

In this sp ecial case we add only one additional parameter. In the region k ≫|κ|

the second term of (6.55) practically does not contribute to the partial cross

section,

4π

sin

. (6.56)

It yields an essential contribution to the cross section when k ≈|κ| and so it

canbeconsideredasacorrection at low energies.

In a general case the DT modiﬁes all partial harmonics and partial shifts.

The DT allows us to construct new solvable models with additional parame-

ters. One of the most imp ortant problems of solvable mo dels is to ﬁt them to

some physically meaningful parameters. For example, in our case the parame-

ter κ can be related to the eﬀective radius of the interaction or the scattering

length. It is well known that the scattering length is deﬁned as derivative

A = −δ

′

(k)atk = 0. Considering (6.55) at low energies, we obtain “renor-

malized” scattering length

(1)

= A +

. (6.57)

6.5 Applications to X

and YX

structures

For the purpose of illustration we consider in this section the scattering prob-

lem for a dressed multicenter potential. The multicenter scattering within

the framework of the ZRP model was investigated by Demkov and Rudakov

182 6 Applications of dressing to linear problems

[114] (eight centers, cube), Szmytkowski and Szmytkowski [421] (four centers,

regular tetrahedron), and others. We analyze here electron scattering by the

and YX

structures within the framework of the ZRP model. At the end

of this section we present a calculation of the electron–silane scattering cross

section with the corrections caused by the dressing integral.

6.5.1 Electron–X

scattering problem

Suppose a structure X

contains n identical scatterers placed at the points

, which involve only s waves. Let R denote the distance between any two

scatterers. There are three such structures in the three-dimensional space: a

line X

, a regular triangle X

, and a regular tetrahedron X

. The partial waves

(r) and phase shifts can be classiﬁed with respect to the symmetry group

representation for the structures X

(n =2, 3, 4), degeneracy b ein g deﬁned by

the dimension of the representation [48]. We use the partial waves for ordinary

ZRPs in a general form,

ψ(r)=



m=1

sin(k|r − r

| + δ)

|r − r

. (6.58)

Our intention is to derive an algebraical equation for the partial phase. The

s-wave boundary condition at the points r

leads to an algebraical problem

for a n ×n matrix with compatibility condition

[p +(n − 1)q](p − q)

n−1

=0,

where

p = akR + R tan δ, q = a[sin(kR)+cos(kR)tanδ].

Then it is easy to show that the phases are determined by the following

expressions:

tan δ

⎧

⎪

⎨

⎪

⎩

−a

kR +(n −1) sin(kR)

R +(n − 1)a cos(kR)

,J=0,

−a

kR − sin(kR)

R − a cos(kR)

,J=1,...,n− 1.

(6.59)

In the special case n = 4 we obtain the phases of the regular tetrahedron

[421]. The integral cross section σ can be expressed a s

σ = σ

+(n − 1)σ

where partial cross sections σ

are given by (6.56). It is easy to r elate a

scattering length for a molecule X

with the boundary parameter a. At large

R the parameter a is reduced to the scattering length for an isolated atom.

Starting from the equation

δ(k)=−arctan



kR +(n − 1) sin(kR)

R +(n − 1)a cos(kR)



6.5 Applications to X

and YX

structures 183

we obtain

= −δ

′

(0) =

naR

R +(n − 1)a

. (6.60)

Testing the result and ta king n =1givesA

= a for arbitrary R. The link

(6.60) deﬁnes the monotonic function saturated at a →∞.

6.5.2 Electron–YX

scattering problem

The structures YX

can be used, for instance, to study a slow electron scat-

tering by polyatomic molecules like H

O, NH

,andCH

. For the sake of

simplicity we suppose that the scatterers X are situated at the vertices of a

regular structure X

.LetD denotes the distance between scatterers Y–X and

R denote the distance between scatterers X–X. In this case, the position of

the scatterer Y is perfectly ﬁxed only if n = 4 (geometric center of the tetra-

hedron), and we have the constraint R =2

D. The partial waves can be

written as (6.58), where the summation should be performed from m =0to

n. The partial phases can be derived analytically. The result is given by the

expression

tan δ

= −a

kR − sin(kR)

R − a

cos(kR)

,J=2,...,n,

and t =tanδ

, J =0, 1, obeys the quadratic equation

(t + a

(

n − 1

+ a



n − 1

sin(kR)

+ t

cos(kR)

)

n − 1



sin(kD)

+ t

cos(kD)



, (6.61)

where a

and a

denote boundary parameters. For large distances we can

interpret these parameters as scattering lengths of isolated atoms. Thus, in the

limiting case when the distance D is very large, the expression for tan δ

passes

to the ﬁrst equation of (6.59) and tan δ

∼−a

k. This situation corresponds

to independent scattering on a molecule X

and atom Y. The substitution

= 0 redu ces tan δ

for the structure YX

to tan δ

for the structure X

Substitution t = −Ak,whereA denotes the scattering length for a

molecule YX

, and passage to the limit k → 0 in (6.61) gives the quadratic

equation with the roots A =0and

= D

+ na

)RD + a

[(n − 1)D − 2nR]

[R +(n − 1)a

− na

. (6.62)

The last root gives a monotonic function of the atomic length a

with the same

features as in the previous section. We believe that the scattering lengths for

isolated atoms do not change much if the atoms form a polyatomic molecule.

184 6 Applications of dressing to linear problems

6.5.3 Dressing and Ramsauer–Taunsend minimum

In the previous sub section we presented a detailed description of new solvable

models for low-energy scattering in the electron–polyatomic molecule system.

Now we compare the results of our model with other theoretical and exper-

imental data. Among all po ssible applications we will discuss the scattering

by the tetrahedral molecule SiH

(silane) because it has th e most interest-

ing point group, namely, the symmetry group of a tetrahedron. We focus our

attention on one distinct feature of the integral cross section, namely, the

Ramsauer–Townsend minimum around approximately 0.28 eV.

Jain et al. [219] classify the minimum as due to the s-wave scattering into

symmetry and attribute the main contribution to the cross section at the

minimum by the p-wave scattering. Also they state that the minimum is the

result of a balance between the a ttractive long-range and repulsive short-range

interactions.

The DT discussed in Sect. 6.4 allows us to correct cross sections at low

energies; thus, using (6.57) and (6.62), we obtain the “renormalized” scattering

length for a molecule YX

. A mo del calculation with (6.55) and (6.61) has

been performed to show that the Ramsauer–Townsend minimum appears as

a consequence of balance between the attractive short-range and zero-range

interactions.

The parameters used in calculation are as follows (in atomic units):

=4.10,R=4.51,κ=0.185,a

=1.88,D=2.762,

which are regarded as constants in the range of interest. The equilibrium dis-

tances R and D were taken from ab initio calculation. The other parameters

were chosen so as to reproduce the realistic low-energy a symptotic of σ and the

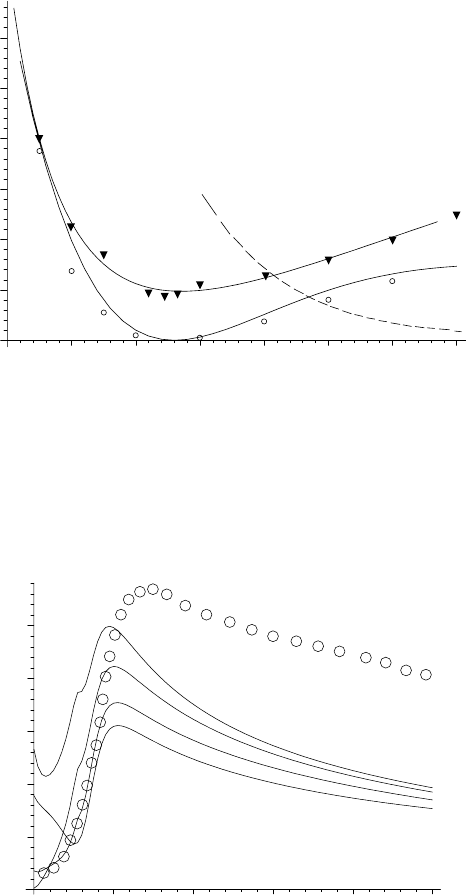
position of the minimum. The result of our calculation is shown as the upper

curve in Fig. 6.4. The circles show the numerical calculation [219]; the tri-

angles and upper curve (least-squares ﬁtting) describe the experimental data

[446]. Our results show that dressing leads to additional ﬁnite-range attractive

interaction which algebraically increases the partial phase (δ

< 0) for partial

wave A

for the YX

structure, and causes the deep minimum near 0.35 eV.

Thus, our partial cross sections coincide well with the results obtained us-

ing other numerical data and coincide in shape with e x perimental data. The

novel feature of our model of electron–molecule scattering is the dependence

of the eﬀective potential on electron momentum (spherical part of the Lapla-

cian). This way we obtain a richer dependence of the scattering parameters

on k, which improves the agreement with experiment in the low-energy region

(Fig. 6.5). It could be considered as an alternative to the Demkov–Rudakov

approach, with generalized partial waves introduced in each step of the dress-

ing procedure. Let us also remind that the model uses only s waves; accounting

forhighertermswouldextend the range of agreement.

We deal with the algebraical expressions for phases of the electron–X

(and –YX

) scattering problem. They are useful to study slow electron

6.5 Applications to X

and YX

structures 185

0.1 0.2 0.3 0.4 0.5 0.6 0.7

σ, 10

-16

E, eV

Fig. 6.4. Integral cross sections for electron–silane scattering around the Ramsauer–

Townsend minimum. The upper curve gives the least-squares ﬁtting to the exper-

imental data [446] (triangles); the lower curve describes our mo del calculation for

partial wave A

; circles denote the calculation for partial wave A

[219]. The dashed

line illustrates the calculation performed in [186]

246810

ICS (10

-16

)

Energy (eV)

Fig. 6.5. Integral cross sections for electron−SiH

scattering on dressed zero-range

potentials at a wider range of energies and diﬀerent values of the matching param-

eter. Experimental results of Wan et al. [446] (circles)

186 6 Applications of dressing to linear problems

scattering by a molecule. We also obtain expressions for scattering lengths

which are helpful to ﬁt the parameters (if the scattering length is known).

Note that in our calculation we do not use scattering lengths of isolated atoms.

Among the most impo rtant aspects of the method is the demonstration of

the power of the DT as applied to a multicenter scattering problem and ZRP

theory. Namely, the ZRP is produced by the DT. Also, these transformations

allow us to correct the ZRP model at low energies.

An alternative approach is formulated for the Calogero–Sutherland model

in [172].

6.6 Green functions in multidimensions

This section is based on [290], where the dressing (factorization) ideas [412,

413, 414] are used to construct the simple poles expansion f or the Jost func-

tion of the one-dimensional Schr¨odinger operator. The representation of the

resolvent of the Schr¨odinger op erator with a reﬂectionless potential does not

contain an integral term. The expression of the potential has a free parameter

that, in turn, allows us to build Green functions for a wide class of multidi-

mensional diﬀerential operators. The explicit form of such a Green function

is given for heat conductivity and wave equations in 2+1 dimensions with an

arbitrary reﬂectionless potential.

6.6.1 Initial problem for heat equation

with a reﬂectionless potential

Consider the nth-order inhomogeneous diﬀerential equation

− L)Ψ = f(x). (6.63)

The operators and the elements Ψ and f of a diﬀerential ring K are deﬁned

in Sect. 3.3. The following proposition is obtained as a consequence of the

results of Sects. 3.1–3.3:

Proposition 6.6. The functions L

ψ,whereL

= ∂ − φ

−1

is the dressing

operator, are solutions of the equation

−

L)Ψ = L

f(x),

where the DT-transforme d op erator

L, the element s, and the equation for it

are given in Sect. 3.3.

Following this statement, we can deﬁne a Green function of the dressed o per-

ator

L. Indeed, take the function f(x, x

′

) in (6.63) as a solution of

f(x, x

′

)=δ(x − x

′

6.6 Green functions in multidimensions 187

and construct a solution of the same equation (6.63):

− L)Ψ = φ



−∞

′′

−1

′′

)δ(x

′′

− x

′



0,x<x

′

φ(x)φ

−1

′

),x>x

′

(6.64)

This results in a Green function that corresponds to the conditions which are

used while the integration on the right-hand side of (6.64) is performed. The

representation for the dressing operator L

= ∂ − φ

−1

is used here.

In a similar way we can perform a manipulation with an initial condition

that is illustrated by the following example.

We proceed from the DT covariance of the heat equation for the function

ρ(τ,x,y),

−ρ

+ ρ

+ u(x)ρ =0. (6.65)

The covariance means the form invariance with respect to the iterated DT

deﬁned by the Wronskian W [φ

, ..., φ

] of the solutions of (6.65):

ρ → ρ[N]=

W [φ

,...,φ

,ρ]

W [φ

,...,φ

]

,u→ u[N ]=u +2(lnW [φ

, ..., φ

])

(6.66)

Consider now a Cauchy problem for (6.65), where u(x)representsthe

reﬂectionless potential [354] and the initial condition is

ρ(0,x,y)=δ(x − y). (6.67)

The problem d escribed by (6.67) is rather general and can be applied as

a model of classical diﬀusion or heat conductivity. We, however, follow the

application in the theory of quasiclassical quantization, where the function ρ

is treated as a density matrix, whence τ stands for inverse temperature [104].

The algorithm to sol ve this problem consists in application of the dressing

procedure organized by the sequence of DTs from (6.66),



∂

∂x

− (ln φ

(x, y))

(0,x,y)=g

(x, y),



∂

∂x

− (ln φ

[1](x, y))

(x, y)=g

(x, y),



∂

∂x

− (ln φ

[k − 1](x, y))

k−1

(x, y)=g

(x, y),

(x, y)=δ(x − y), 2 ≤ k ≤ N, (6.68)

and the following theorem:

Theorem 6.7. The function ρ[N] being built by (6.66) will be a solution of

the problem (6.65) and (6.67) with the p otential u[N],ifρ(τ,x, y) is a solution

of (6.65) with the initial condition ρ

(0,x,y).

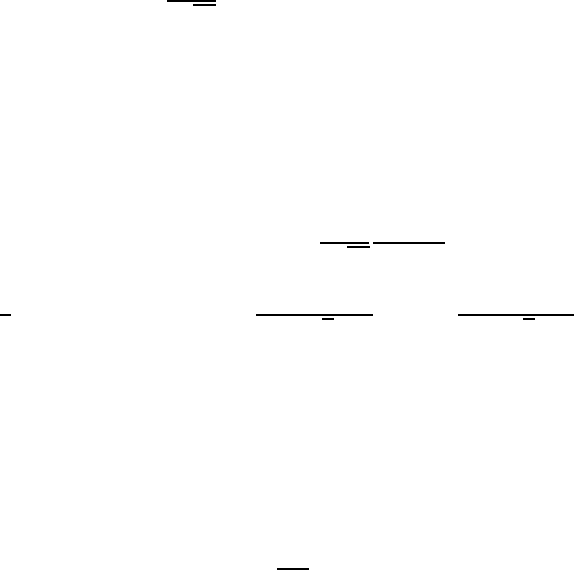
188 6 Applications of dressing to linear problems

This result is used when static solutions of the φ

model are quantized by

means of the Riemann ζ(s)-function [248] expressed via the Green functions

of (6.65) [285]. The one-loop correction to the action is obtained directly as

= −ζ

′

(0).

Example 6.8. The most popular example of the kink is obtained in this scheme

by means of the DT applied to zero seed solution u =0.Thesolutionρ of

(6.65) with ρ

as the initial condition for this case is a simple heat equation

solution:

ρ(τ,x,y)=

√

πτ



∞

−∞

(z,y)exp



−(x − z)

/4τ



dz.

The initial condition ρ

is evaluated by direct integration in (6.68):

(x, y)=φ

(x)



−1

(y),x>y,

0,x<y.

(6.69)

The Green function ρ[2] (density matrix) for the kink solution as the potential

is built by the twofold DT in accordance with the Wronskian formula (6.66):

ρ[2](τ,x, y)=exp



−

√

πτ

(x − y)

4ν(τ)



(6.70)



m=1

(x)ψ

)

(

erf



x − y +2b

√



− erf



x − y − 2 b

√

)

where erf(x) is the probability integral [206].

6.6.2 Resolvent of Schr¨odinger equation with reﬂectionless

potential and Green functions

Some analytic properties of the resolvent kernel from the previous subsection

give the possibili ty to generalize the construction. Let the operator

L = −

+ u(x) (6.71)

contain the function u(x) which corresponds to the reﬂectionless potential

[354]. The Jost function ψ(x, k)satisﬁes

lim

x→∞

ψ(x, k)exp(−ikx)=1.

It has n poles in the lower half k-plane that correspond to bound states

(discrete sp ectrum), i.e., eigenvalues of the operator (6.71): λ

= −b

, b

0, m =1,...,n. Eigenstates ψ

are normalized as

lim

x→∞

exp(b

x)=1.