Doktorov E.V., Leble S.B. A Dressing Method in Mathematical Physics

Подождите немного. Документ загружается.

6.2 Integrable potentials in quantum mechanics 169

3. There are two roots ρ

<ρ

; the case of the only simple ro ot ρ

= ρ

is in-

cluded as well. Then R =(−∞,ρ

] or R =[ρ

, ∞),andU(x) is nonsingu-

lar. Both z(x) and U (x) are even functions. The potential is nonsingular,

iﬀ

Q(ρ)=P

′

(x)/2 or Q(ρ)=3P

′

(x)/2.

4. There are two roots ρ

<ρ

and R =[ρ

,ρ

]. Then both z(x) and U (x)

are periodic functions and U(x) is singular.

Scattering amplitudes for the shap e-invariant potentials are calculated by

the dressing metho d; see also [236].

Algebraic deformations

Algebraic deformations of the shap e-invariant p otentials leave the potentials

and eigenfunctions in the class of elementary functions. They are a backward

DT which is g enerated by the factorization function φ that is a product of

exponential and rational functions. We use the notion of a function f of the

polynomial type, if (log f)

′

is a rational function.

The prop (factorization [190]) function is

φ(x)=exp{ p[z(x)]}f[z(x)]. (6.24)

Owing to (6.22) and possibility 3, the function p is polynomial and the func-

tion f(z) is a hypergeometric function of the polynomial type.

As is seen from Table 6.1, in case Ib we obtain nontrivial deformation of

the oscillator potential if the solutions y(z)=Φ(a, c, z) of the equation

′′

+(c − z)y

′

− ay =0

are expressed in terms of the generalized Laguerre po lynomials L

,m =

0, 1, 2 ,... [206]. Here a = −m and c = α + 1. One of the solutions is used

in the deformation of the harmonic oscillator potential [134, 135], namely, the

function

=exp(z)Φ(−m, c, −z).

We will include a shift by x

in the transform (6.24), or z =(x −x

)

,which

allows us to deform the potential in a nonsymmetric way.

The function

φ(x; λ, A, B)=



AΦ(1/4 − λ/4, 1/2; x

)+BxΦ(1/4 − λ/4, 3/2; x

)



exp(−x

/2)

produces a general solution of the equation

−φ

′′

+ x

φ = λφ.

170 6 Applications of dressing to linear problems

When λ =2n + 1, we have bound states proportional to exp(−x

/2), and,

by the nodeless solutions (λ<1), the prop (factorization, superpotential)

function is written as

(m)

= φ(x; −1 − 4m, 1, 0) = exp(−x

/2)y

). (6.25)

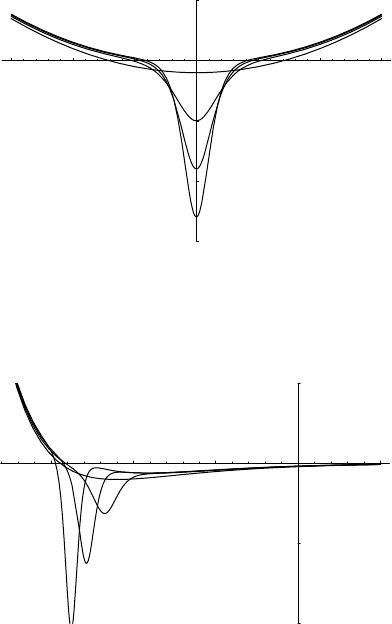
This produces a deformation of the harmonic oscillator potential (Fig. 6.1)

(m)

= x

− 2



ln exp(−x

/2)



Similar results for the Morse potential deformation are demonstrated by

Fig. 6.2.

The regular solutions of the hypergeometric equation

z(1 − z)f

′′

(z)+[c − (a + b +1)z]f

′

(z) − abf (z)=0

-3 -2 -1 1 2 3

-10

-20

-30

Fig. 6.1. The result of deformations in the case of the harmonic oscillator for

m =0, 1, 2, 3 [190]

-3 -2 -1 1

-100

-200

100

Fig. 6.2. Deformations of the Morse potential for m =0, 1, 2, 3 [190]

6.2 Integrable potentials in quantum mechanics 171

-4 -2 2 4

-20

-40

Fig. 6.3. Algebraic deformations of the hyperbolic P¨osc hl–Teller potential,

m =0, 1, 2, 3 [190].

are given by the Gauss hypergeometric function f(z)=F (a, b, c; z). This

function is of the polynomial type if a = −m (or b = −m), where m is

an integer [207]. In this case the solutions are given by the Jacobi polynomial

(α,β)

(z) which is used in deformations of the P¨oschl–Teller potential (Fig. 6.3).

Note that a bigger m corresponds to a deeper well.

6.2.3 Coulomb potential as a representative of singular potentials

The radial Schr¨odinger equation,



−

l(l +1)

+ u − E



(r)=0, (6.26)

is transformed to (6.19) by the transformation ψ

= φ

/r:



−

l(l +1)

+ u − E



(r)=0. (6.27)

Hence, the corresponding chain equation is equivalent to that obtained in the

one-dimensional case; see (6.9) and the instructive example in Sect. 4.1.

The general shape-invariant singular potential is given by (6.16). Equation

(6.17) for the iterated potential yields

(ξ

/ψ − 1)

(x + B/A)

(ξ

λ/ψ + η

)

(x + B/A)ψ

+(ξ

λ/ψ + η

)

+ μ

, (6.28)

where

= −

(ξ

j+1

− ξ

)

j+1

− ξ

,ψ= ξ

j+1

− ξ

172 6 Applications of dressing to linear problems

The condition of existence of the representation (6.16) gives the following for

the spectrum:

j+1

= μ

(ξ

j+1

− ξ

j+1

)

j+1

− ξ

The choice B = 0 that corresponds to the choice of the form function

a(r)=(λr +1)/r gives

(ξ

/ψ − 1)

− 2

(η

− ξ

φ/2ψ)

rψ

+(η

− ξ

φ/2ψ)

+ μ

. (6.29)

Being the reduction of (6.28), this relation leads to

φ =2

j+1

− ξ

j+1

+ ξ

Let us choose the potential u in the Coulomb form:

u = −Ze

/r.

The coincidence between the r-dependent parts (6.29) and the double poten-

tial part of (6.27) yields two constraints for the constants:



− 1



= l(l +1),

j+1

− η

j+1

+ ξ

= −Ze

The ﬁrst relation gives ξ

recursively as a function of l; the second one yields

via l, Z,ande. This means that (6.11) and the dressing of the basic state

solve the Coulomb quantum problem, producing the spectrum of E in (6.27)

and eigenfunctions via reproducing the Rodrig-like formulas.

On the other hand, the classiﬁcation of shape-invariant potentials includes

the Coulomb and r elated singular potentials [92, 100]; hence, the Coulomb

potential deformations can b e considered along the lines of Sect. 6 .2.

Remark 6.3. An interesting extension of the above results is ava il able. Let us

add the so-called Manev p otential [370] to the Coulomb ﬁeld (α = −Ze

u =

the angular momentum term being incorporated in the last term. The condi-

tions of coincidence of this potential with one of (6.29) yield constraints



− 1



= β,

j+1

− η

j+1

+ ξ

= α.

Note also that [370] contains the paper of Todorov entitled “On Some Fac-

torization Statements and Applications” that relates to the ladder (named

staircase) operators in the case of inﬁnite matrices with a ﬁnite number of

nonzero matrix elements in each row/column.

6.2 Integrable potentials in quantum mechanics 173

6.2.4 Matrix shape-invariant potentials

For the case of the matrix Schr¨odinger equation we reproduce here in more

detail the general formalism from Chap. 2. The DT for the one-dimensional

matrix problem

∂

+ a

∂ψ

∂x

+ a

ψ = Eψ (6.30)

has the form

(1)

= ψ

− φ

−1

ψ, (6.31)

where s = φ

−1

is constructed by matrix solution φ of (6.30) for a diﬀerent

eigenvalue E

′

The transformation can be also deﬁned by means of th e covariance prop-

erty of the Schr¨odinger equation with respect to a transformation of a

wave function. The principal statement (on the covariance) formally yields

(∂ = ∂/∂x)

(1)

= Eψ

(1)



n=0

(1)

∂

; (6.32)

explicit expressions for a

(1)

are given in [289] for an arbitrary-order operator.

We cite here the matrix Darboux dressing formulas for the second-order op-

erator. The coeﬃcient a

does not transform, so it is chosen as a

= −1/2,

while the transform for a

generally contains the commutator

(1)

= a

+[a

,s], (6.33)

which for the given a

is zero. Finally, slightly changing the notations, the

transforms are

(1)

= ψ

− sψ, (6.34)

(1)

= a

+ a

′

+[a

,s]+2a

′

+ a

′

s +[a

,s]s = a

+ a

′

− s

′

where the commutator [a

,s] = 0 and the primed function is the shortcut for

the derivatives in x. The functions ψ

(1)

and u

(1)

are again named “dressed”

ones, and the auxiliary solutions of the problem (6.30) are referred to as the

“prop” functions. The eigenfunction and the potential (ψ and u here) we start

with are called the “seed” ones. Let us mention that the proof of the Darboux

covariance relation includes a link that in the theory of solitons [324] is named

the (general) Miura transformatio n (Chap. 3) and is solved identically by the

substitution s = φ

−1

. We, however, do not use this fact, and go in an

alternative way. Notice that in the case of the radial Schr¨odinger equation

= −1/r, which also simpliﬁes the transform (6.34).

174 6 Applications of dressing to linear problems

6.3 Zero-range potentials, dressing,

and electron–molecule scattering

Following Andrianov et al. [25], the Darboux formulas can be applied in multi-

dimensional space in combination with those for the radial Schr¨odinger equa-

tion [324, 391]. This approach makes it po ssible to use the DT technique to

work with an improved version of a ZRP mo del.

Our aim here is to dress the ZRP by means of a special choice of the DT

in order to widen the possibilities of the ZRP model. The DT modi ﬁes the

generalized ZRP boundary condition and creates a potential with arbitrarily

arranged discrete spectrum levels for any angular momentum l.

6.3.1 ZRPs and Darb oux transformations

Our statement consists in the fact that generalized ZRPs [38] appear as a

result of the DTs applied to zero potential. In order to demonstrate this we

consider a radial Schr¨odinger equation



−

l(l +1)

+ u

− E



(r) = 0 (6.35)

for partial wave ψ

with orbital momentum l. The atomic units  = m

are used throughout the present section. Here u

, l =0, 1, 2,..., are potentials

for the partial waves with an asymptotic at inﬁnity

(r) ∼

sin(kr −

lπ

+ δ

)

where δ

are partial phase shifts. Equation (6.35) describes scattering of a

particle with energy E and momentum k =

√

2E by the rapidly decreasing

potential u

. In the absence of the potential, partial shifts δ

= 0 and partial

waves can be expressed via spherica l functions ψ

= j

(kr).

It is k nown that (6.30) with

= −

l(l +1)

+ u

(6.36)

is cova riant with respect to the DT (6.33) and (6.34). The prop function φ

plays an important role when applying the DT because it is used to calculate

s. The function φ is a solution of (6.35) at a particular value of energy E =

−κ

/2, where we assume κ is a real number. If κ is a complex number, then

the dressed potential will be a complex function in general.

Let us demonstrate how a generalized ZRP can be produced by the DT.

It is convenient to use a sequence of DTs (Crum formulas [94] with the wave

and prop functions multiplied by r), which for our equation look like

→ ψ

(1)

=const·

W (rψ

,rφ

,...,rφ

2l+1

)

rW(rφ

,...,rφ

2l+1

)

, (6.37)

→ u

(1)

= u

− [ln W (rφ

,...,rφ

2l+1

)]

′′

. (6.38)

6.3 Zero-range potentials, dressing,and electron–molecule scattering 175

Here W is the Wronskian, φ

are prop functions, and the double prime stands

for ∂

/∂r

. The transformation (6.37) combines the solution ψ

and 2l +1

solutions φ

. The Crum formulas result from the replacement of a sequence

of 2l +1 ﬁrst-order transformations by a single (2l+1)th-order transformation

which happens to be more eﬃcient in practical calculations. In order to obtain

the ZRP, we start from zero potential and use prop functions

= h

(1)

(κ

r), (6.39)

where κ

are solutions of the algebraical equation κ

2l+1

=iα

. Here we assume

is a real number. The explicit form of the spherical functions h

(1)

(kr)=n

(kr)+ij

(kr),h

(2)

(kr)=n

(kr) −ij

(kr). (6.40)

The spherical functions j

and n

are r elated to usual Bessel functions with

half-integer indices [30]. They obey the asymptotic at inﬁnity r →∞of the

form

(kr) ∼

sin(kr −

lπ

)

(kr) ∼

cos(kr −

lπ

)

. (6.41)

For our purpose, it is important that in the vicinity of zero the spherical

functions have asymptotic behavior

(kr) ∼

(kr)

(2l +1)!!

(kr) ∼

(2l − 1)!!

(kr)

l+1

. (6.42)

Note the double factorial (2l − 1)!! satisﬁes the relation (2l)! = 2

l!(2l − 1)!!

The asymptotic for h

(1,2)

(kr) can b e obtained by combining (6.42) in ac-

cordance with (6.40). For example, at inﬁnity use of (6.41) leads to

(1)

(kr) ∼ (−i)

ikr

(2)

(kr) ∼ i

−ikr

Direct substitution of (6.39) into the Wronskian gives

W (rφ

,...,rφ

2l+1

)=const.

This means that the dressed potential is again the ZRP, u

(1)

(r>0) = 0.

The transformation (6.38) allows us to calculate potential for r>0. We state

that the DTs also yield a generalized ZRP at r = 0. In order to prove this,

we perform the transformation (6.37) and show that ψ

(1)

is a solution for a

generalized ZRP. Since the potential is zero in the region r>0, it is suﬃcient

to determine the asymptotic of the wave function. Substituting ψ

= j

(kr)

into the Crum formulas, we obtain

(1)

=const·

W [rj

(kr),rφ

,...,rφ

2l+1

]

rW(rφ

...,rφ

2l+1

)

∼



(−i)

ikr

∆(ik, κ

,...,κ

2l+1

)

∆(κ

,...,κ

2l+1

)

− i

−ikr

∆(−ik, κ

,...,κ

2l+1

)

∆(κ

,...,κ

2l+1

)



176 6 Applications of dressing to linear problems

where ∆ is the Vandermond determinant. Considering it as the product

∆(ik, κ

,...,κ

2l+1

)=const·

2l+1



m=1

(κ

− ik),

we obtain an asymptotic which coincides with the asymptotic of the solution:

(1)

=const· [h

(1)

(kr)e

2iδ

− h

(2)

(kr)], exp(2iδ

2l+1



m=1

− ik

+ik

. (6.43)

It is easy to show that the wave function (6.43) describes a scattering of the

partial wave with orbital momentum l by the generalized ZRP . The potential

is conventionally represented as the boundary condition at r =0forthewave

function. This fact can be veriﬁed b y direct substitution into the boundary

condition for the generalized ZRP:

(d/dr)

2l+1

l+1

(1)

l+1

(1)



r=0

= −

l!α

(2l − 1)!!

, (6.44)

where α

is the inverse scattering length for the partial wave with orbital

momentum l. Recall that at low energies tan(δ

) ∼−a

2l+1

for a short-range

potential, where a

is the scattering length. In the special case of l =0we

obtain (ln rψ)

′

= −α. This genera lized boundary cond ition can be obtained

from the asymptotic of the wave function in the vicinity of zero, which was

used in [38]. Let us consider the scattering matrix on the complex k-plane.

Each element exp(2iδ

)has2l + 1 poles at the points k =iκ

, which lie on a

circle in the complex plane. Since the bound states correspond to the poles on

the imaginary positive semi-axis in the complex k-plane, a bound state exists

only if α

> 0andl isanoddnumberorifα

< 0andl is even. Otherwise

the ZRP has an antibound state.

The ideas of the ZRP approach were recently developed [38, 116, 282] to

extend the limits of the traditional treatment by Demkov and Ostrovsky [115]

and Albeverio et al. [21]. The advantage of the theory is the possibility of ob-

taining an exact solution of the scattering pr oblem. The ZRP is conventionally

represented as the boundary condition on the wave function at some point.

Alternatively, the ZRP can be represented as a pseudop otential [77, 116].

There is some “generalization” of the ZRP theory, when the inverse scat-

tering length in the original boundary condition is replaced by −kcotδ for

l = 0. In such a model the ZRP may have two (or more) bound states with

nonorthogonal wave functions. This problem does not appears in our model

because our potential has only one bound state. However, we note that a

generalized ZRP has another problem: the bound state with orbital momen-

tum l>0doesnotbelongtoL

(the zero-range eﬀect). But we think that

this problem is not fatal because this mo del reasonably describes low-energy

scattering.

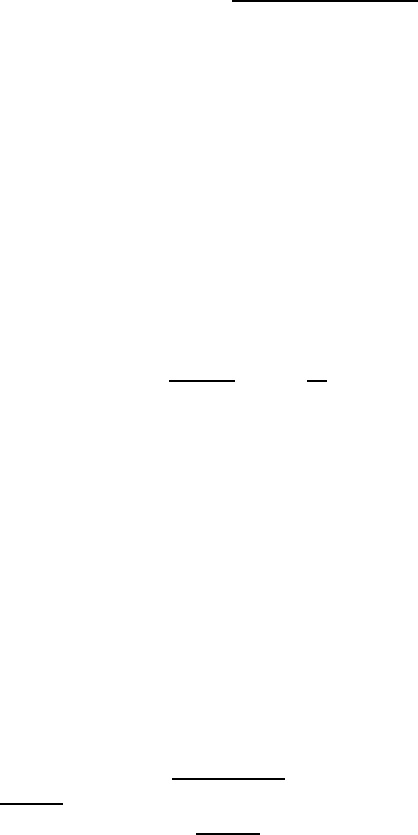
6.3 Zero-range potentials, dressing,and electron–molecule scattering 177

Example 6.4. There is a simple example which proves our observation: the

ZRP can be produced by the DT. Let us consider transformation of the reg-

ular solution ψ =sin(kr)/r with the prop function φ =exp(αr)/r. Direct

calculation yields the wave function

(1)

=const·(ψ

′

− sψ)=

sin[kr − arctan(k/α)]

, (6.45)

which satisﬁes the original ZRP condition with the inver se scattering pa-

rameter α. Repeating the transformation with φ =exp(−αr)/r,weobtain

(2)

= ψ. This example shows a relation between the ZRP and the DT.

6.3.2 Dressing of ZRPs

We have shown the gener alized ZRPs appear as a result of application of the

DT to the seed so l u t ion. In this connection we can raise a problem of subse-

quent dressing of the ZRP. In the particular case of only one prop function φ

the Crum formulas correspond to the usual DT:

(1)

=const· (ψ

′

− sψ

),s=(lnφ)

′

(1)

≡ a

(1)

−

l(l +1)

= u

− s

′

, (6.46)

where we suppose the potential u

describes the ZRP. The functions ψ

and

φ are solutions of the Schr¨odinger equation (6.35). Since the p otential u

(r>

0) = 0, the solution φ can be wr itten as a linear combination of spherical

functions,

φ = Cn

(iκr)+C

(iκr), (6.47)

where C, C

,andκ are parameters. Note the dressed potential u

(1)

is real

for real prop function φ; hence, the parameters should be real. The direct

application of (6.31) allows us to calculate the potential in the range r>0,

but not at r = 0! In order to solve this problem, we consider φ in the vicinity

of zero. There are two diﬀerent cases. The spherical function properties show

that in the case C = 0 the leading term in φ is r

andinthecaseC =1this

term looks like r

−l−1

. Therefore, the dressed coeﬃcient a

(1)

has the following

asymptotic at zero:

l(l +1)

+ u

(1)

∼

⎧

⎪

⎨

⎪

⎩

(l +1)(l +2)

, when C =0,

l(l − 1)

, when C =1.

As regards all the other possible cases, it is easy to see that they lead to

the a bove results. According to (6.46), the dressed potential u

(1)

decreases

as exp(−2|κ|r) at inﬁnity. Thus, the DT produces a short-range core of the

178 6 Applications of dressing to linear problems

centrifugal type (which depends on angular momentum l) in the potential.

In this situation the boundary condi ti ons on the dressed wave functions ψ

(1)

require some modiﬁcation. We believe that in the genera l case the dr e ssed

ZRP is conventionally represented as the bou n d ary condition

(d/dr)

2m+1

m+1

(1)

m+1

(1)



r=0

=const,

where m = l +1 for C =0andm = l − 1forC = 1. However, repeating

the DT for other values of κ and combining the results for C =0and1,we

can remove the short-range core. In the a bsence of the short-range core the

boundary co ndition looks like (6.44). The sequence of N DTs leads to new

poles of the S matrix which do not depend on C

exp

2iδ

(N)

− ik

2l+1

+ik

2l+1



m=1

− ik

+ik

. (6.48)

Thus, we can use the DT in order to add (or remove) poles of the S matrix. The

next step in the dressing procedure is the determination of the free parameters

of the solutions φ. Changing parameter C

, we obtain potentials with identical

spectra, called the phase-equivalent p otentials. The transformation of this

kind is also known as the isospectral deformation.

Example 6.5. The simplest case l = 0 is instructive. Consider the original ZRP

at r = 0 with the wave function (6.45). We can choose the solution φ as

φ =

cosh(κr)

This choice corresponds to the parameters C =1andC

=0.Forbrevitywe

omit the index l =0.TheDT(6.31) gives rise to the following property of

the dressed wave function:

(rψ

(1)

)

′

rψ

(1)



r=0

+ κ

which slightly diﬀers from the usual boundary condition in ZRP theory

(lnrψ)

′

= −α. The dressed potential has the short-range tail:

(1)

(r>0) = −

cosh

(κr)

. (6.49)

Our investigations show that some particular values of C

can give a long-

range interaction which decreases like ∼ r

−2

The model we study describes the scattering of an electron on a com-

pound particle. There were attempts to account for this important circum-

stance by means of matrix potentials to be applied not only to the well-known