Doktorov E.V., Leble S.B. A Dressing Method in Mathematical Physics

Подождите немного. Документ загружается.

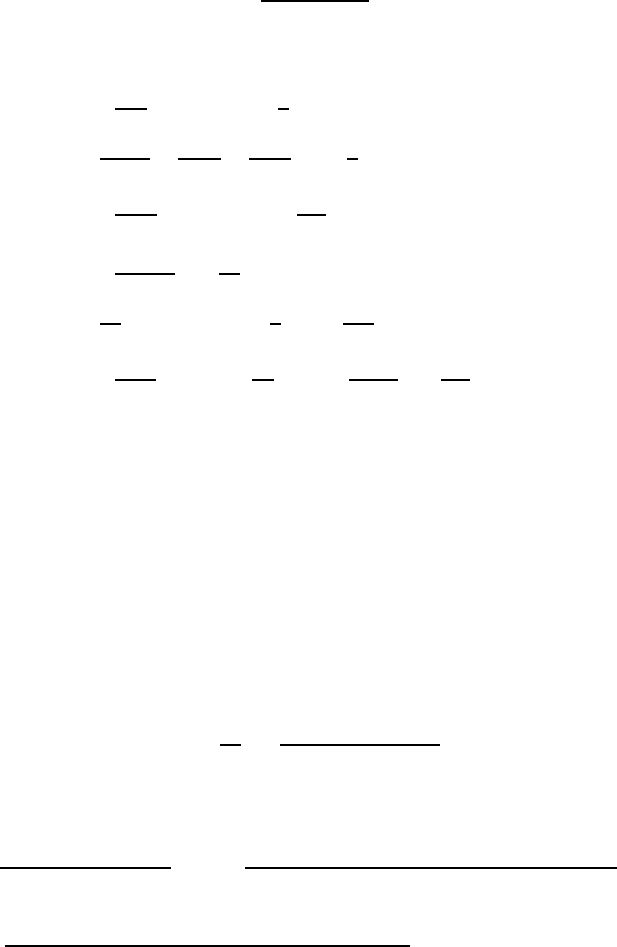
5.6 Generalized Moutard transformation for tw o-dimensional MKdV equations 159

and (w = ψ/φ)

= θw

= −

(1/θ)

= θw

xxx

+ c

yyy

+ c

with

= −

+ θ, c

θ(ln θ

)

− θ

φφ

−



(ln θ

)

− θ





3φ

+ A − u



θ −

= −

(θ

+ u

φφ

)

(

3θu

− φφ



B −



)



3φ

− B



θ +



2θ

−

3θθ



− u

θ.

The 1-form dQ is closed,

1,y

= Q

2,x

1,t

= Q

3,x

2,t

= Q

3,y

It is easy to verify that the (L, A) pair (5.66) is covariant with respect to the

generalized Mourtard transformation (5.67).

5.6.2 Solutions of two-dimensional MKdV (BLMP1) equations

Now we use these transformations to construct exact solutions of the two-

dimensional MKdV equations (5.24). Let us choose u = const and A = B =0.

We will consider two examples.

1. If we take the solution of (5.66) as φ =sinhξ,where

ξ = ax +

y +

− a

)(u

− a

)

t (5.68)

with real a = const, then using (5.67) we get a new solution of the two-

dimensional MKdV equations,

˜u =



2η − a

sinh(2ξ)



2η + a

sinh(2ξ)

A =

16a

sinh ξ



sinh ξ − (u

− 3a

)η cosh ξ



[2η + a

sinh(2ξ)]

B =

16av

cosh ξ



cosh ξ − (3u

− a

)η sinh ξ



[2η + a

sinh(2ξ)]

160 5 Dressing in 2+1 dimensions

where

η = a

y − a

x)+(u

− a

)(3u

+3a

+2a

)t. (5.69)

2. To construct the algebraic solutions of (5.44), we choose the solutions of

(5.66) as

φ =(−1)



dkζ(k)exp[ξ(k)]

δ(k − k

with ξ(k) from (5.68), a = a(k), and β>k

>α>0, where ζ(k)isan

arbitrary diﬀerentiable function. For n =1,ζ =1weget

˜u =

u(a

− 2η

− 2a

η)

2η

+2a

η + a

A = −

+3a

)η(η + a

)

(2η

+2a

η + a

)

B =

(3u

+ a

)η(η + a

)

(2η

+2a

η + a

)

(5.70)

with η from (5.69) and a = a(k

). Equation (5.70) is a simple nonsingular

algebraic solution of the two-dimensional MKdV equations.

There is a group of equations for which the dressing technique is directly

applied. The BLMP2 equation is a generalization of the Nizhnik–Veselov–

Novikov equation [58]. There is another new integrable equation that is usually

called the Boiti–Leon–Pempinelli (BLP) equation. It was proposed and stud-

ied in [65]. An integrable generalization of the sine and sinh–Gordon equations

in two spatial dimensions was proposed in [64].

Applications of dressing to linear problems

The dressing procedures, fo l l owing our “extended” understanding of this

ideology, have been used for years to solve linear problems. In this chapter

we concentrate on some recent results obtained along these lines. We observe

considerable reciprocal inﬂuence of the nonlinear theory on linear methods,

in particular via a sy stematic application of the Lax representation developed

previously when studying nonlinea r systems.

We show how to dress a seed solution of a one-dimensional second-order

linear diﬀerential equation when the corresponding operator allows explicit

factorization. We also show how the Darboux transformation (DT) theory

appears in this framework and produces the so-called integrable or solvable po-

tentials entering linear diﬀerential equations. The important and far-reaching

example of solva ble potentials is represented by the famous regular shape-

invariant p otentials introduced by Gendenstein [179] (see also [412] and refer-

ences therein). We could mention as well other classes of potentials, like those

obtained by algebraic deformations [190], singular (pointlike of the Coulomb

type or zero-range) potentials [284], and matrix potentials on the whole axis

or half-axis.

There is an excellent book [367] on applications of the Lax representation

to classical mechanics. The integrability is established and exploited by means

of the Li e algebra technique. Here we point out some possibilities directly

related to the dressing scheme we develop; see also the recent boo k [368].

Generally, an evolution equation

˙x

= F

(x), (6.1)

can be written in the form of the Lax representation (by means of the L–M

pair [367]), so that (6.1) is equivalent to

L =[M, L]. (6.2)

Such an idea of Lax [263] is traced throughout the previous chapters of this

book. He showed that the spectrum of the matrix operator L does not depend

161

162 6 Applications of dressing to linear problems

on time, when L evolves a s L(t)=UL(0)U

−1

, U

U = 11 (hence the name

isospectral representation [338]). Such an approach constitutes the main algo-

rithm of seeking for integrability: eigenvalues λ of the matrix L are conserved

quantities (

λ = 0). Historically, the Lax representation was found “experi-

mentally” [152].

There are also attempts to apply these ideas to 2+1 dimensions by means

of the Moutard transformations [288, 369]. Speciﬁc results of the application

are still rather poor [30, 290]. In higher dimensions the search was launched

by [25] with increased eﬀorts till now [28, 29].

In Sect. 6.1 we introduce the gauge–Darb oux transformation (GDT) and

the auto-gauge–Darboux transformation (auto-GDT) as a manifestation of the

covariance property of the linear equation under consideration. These trans-

formations permit us to derive recurrent relations between solutions of a given

equation with diﬀerent values of the set of parameters. Quantum-mechanical

integrable potentials are discussed in Sect. 6.2 from the point of view of dress-

ing. We consider shape-invariant nonsingular potentials of the Schr¨odinger

equation and their algebraic deformations, as well as the Coulomb-like singu-

lar potentials and their shap e-invariant iterations. A new approach to solve

the Schr¨odinger equation with a zero-range potential (ZRP) is described in

Sect. 6.3. We show that dressing of such a potential by means of a sp ecial DT

improves t he ZRP model, especially for low-energy scattering. Further devel-

opment of this method is illustrated in Sects. 6.4 and 6.5 by solving the prob-

lem of multicenter scattering . We perform a detailed analysis of the electron–

scattering and clarify the nature of the Ramsauer–Townsend minimum

in the cross-section spectrum. In Sect. 6.6 we use the dressing technique to

construct Green functions for a wide class of multidimensional diﬀerential op-

erators with reﬂectionless potentials. Finally, in Sect. 6.7 we demonstrate the

possibility to construct supersymmetric quantum-mechanical po tentials with

a preassigned discrete spectrum by means of the DTs. We explicitly manage

the spectrum by deleting o r adding energy levels.

6.1 General statements

In Sect. 2.4 general dressing formulas for co eﬃcients of operators p olynomial

in D were derived. In Sect. 3.1 the origin of the DT and gauge transforma-

tions (GT) were discussed. We outline now the algorithm of eigenfunction

construction on the basis of these results. The theory goes back to the book

[324], where the simplest case of a quantum harmonic oscillator is discussed

from this point of view. The combined GDT was introduced in [466], where

the covariance theorem (including dressing formulas for potentials) for a wide

class of operators wa s proved. A development of this technique was given in

[381]. Recall that in Sect. 2.11 a combination of GT and DT was applied to

solve a linear diﬀerential-diﬀerence pr oblem that enters the Lax pair for the

Nahm equations.

6.1 General statements 163

6.1.1 Gauge–Darbo ux and auto-gauge–Darboux transformations

Following [466] and [380], we consider the linear equation

+ p(x; ν

, ..., ν

)ψ

+ q(x; ν

, ..., ν

)ψ = λh(x; ν

, ..., ν

)ψ + f(x; ν

, ..., ν

(6.3)

The covariance of this problem with respect to a substitution (we call it a

GDT)

ψ →

ψ = s(ψ

− σψ), (6.4)

where s and σ depend on x, means a form invariance of (6.4) with the only

change of the coeﬃcients in accordance with

h →

h = h, p → ˜p = p − [ln(hs

)]

q → ˜q = q + p

− [p + σ − (ln s)

](ln h)

+2σ

+(lns)

[ln (hs

)]

− s

/s,

f →

f = sf

− s [σ + s(ln h)

] . (6.5)

We call the GDT (6.4) and (6.5) as the auto-GDT if

˜p (x; ν

,...,ν

)=p (x;˜ν

,...,˜ν

), (6.6)

˜q (x; ν

,...,ν

)=q (x;˜ν

,...,˜ν

), (6.7)

f(x; ν

,...,ν

)=f(x;˜ν

,...,˜ν

), (6.8)

i.e., the GDT action is equivalent to the transformation of the spectral pa-

rameters. This notion accumulates the shape-invariant potentials of quantum

theory that are discussed in the next section. In [190] the function σ is called

the factorization dressing function, while in [92] it is referred to as the super-

potential. The GDT allows us to obtain recurrent relations between solutions

with diﬀerent values of the parameter set. In the particular case of special

functions of mathematical physics, these relations are exactly the recurrent

relations between them. Further discussion of this subject is given in Chap. 4.

The algorithm of working with the auto-GDT consists mainly of two steps:

1. We solve a diﬀerential equation (6.3) for λ = 0 and then, choosing h, ﬁnd

a solution with λ =0.

2. By means of the transformation (6.5) we go to a solution of the same

equation (6.5) with λ = 0 which is a solution of the initial equation with

some other set of the parameters ˜ν

,...,˜ν

Consider an example of the Gegenbauer equation

Gψ ≡

(2μ +1)x

− 1

dψ

−

n(2μ + n)

− 1

ψ =0.

164 6 Applications of dressing to linear problems

The choice of h =(x

− 1)

and of the ﬁxed solutions of Gψ = λhψ as

1,2,3

=(x

− 1)

1,2,3

with

= n/2,β

= −n/2 − μ, β

=1/2 −μ,

1,2

=4β

1,2

(β

1,2

− 1) + 2β

1,2

(2μ +1),λ

=4μβ

− n(2μ + n)

forms the GDT operators

1,2,3

=(x

− 1)



−

2β

1,2,3

− 1



by means of (6.4).

The transformed parameters take the form

˜n

= n − 1,μ

= μ,

˜n

= n +1,μ

= μ,

˜n

= n +1,μ

= μ − 1.

The ﬁrst two GDTs correspond to the known op erators that link the Gegen-

bauer functions.

6.1.2 Chains of shape-invariant superpotentials

The dressing chain equatio n (Chap. 4) is nothing more than the result of sub-

stitution of the Miura link in the DT formula. For convenience we reproduce

it here:

(σ

+ σ

i+1

)

′

= σ

− σ

i+1

+ μ

− μ

i+1

. (6.9)

There is a class of p otentials of the S chr¨odinger one-dimensional equation that

are obtained by closure of the dressing chain (see Sect. 4.1 ), i.e., under the

condition posed to the j-times iterated function (superpotential) σ

= ξ

a(x)+η

,j=0, ±1,.... (6.10)

It is a kind of the superpotential parameterization. The compatibility of this

condition with the chain equation (6.9) yields the condition for the function

a(x) that ﬁxes the shape of superpotentials and hence of the p otential u

(here

we use notations from Sect. 3.1) by means of the Miura link

= σ

′

+ σ

+ μ

. (6.11)

This procedure introduces one more (spectral) parameter μ

into the scheme.

Nowwecanwritetheequationfora(x) in the standard Riccati equation form:

′

+ ψa

+ φa + χ =0, (6.12)

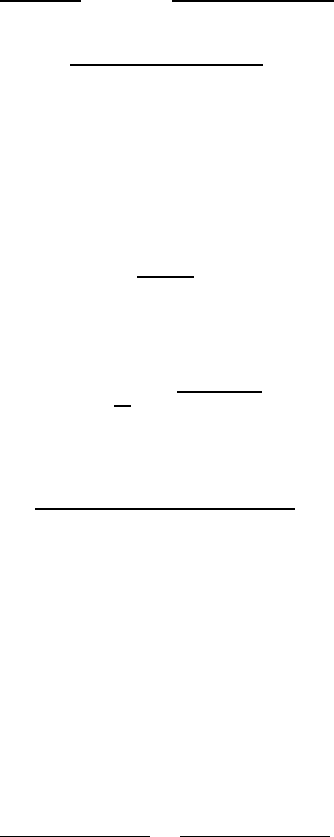
6.1 General statements 165

where

ψ =

j+1

− ξ

j+1

+ ξ

,φ=

2(ξ

j+1

− ξ

)

j+1

+ ξ

χ =

j+1

− η

+ μ

j+1

− μ

j+1

+ ξ

. (6.13)

The diﬀerential equation (6.12) with constant coeﬃcients is transformed to

the second- order linear equation

′′

+ Py

′

+ Qy = 0 (6.14)

with P = φ and Q = ψχ by the standard substitution (for nonzero ψ)

a =

(ln y)

which can be used for a classiﬁcation of the superpotentials. Indeed, the char-

acteristic equation for (6.14) is the quadratic equation, whose solutions

1,2

= −



/4 − Q

yield the ﬁrst class superpotentials as solutions of (6.12) with λ

= λ

a =

Aλ

exp(λ

x)+Bλ

exp(λ

ψ[A exp(λ

x)+B exp(λ

x)]

. (6.15)

The second class corresponds to the coincidence of the roots of P

/4 −Q =0,

i.e., to the condition for the parameters of the superpotential:

4ψχ = φ

Inserting here the deﬁnitions (6.13) of the Riccati equation coeﬃcients leads

(ξ

j+1

− ξ

j+1

)

=(ξ

j+1

− ξ

)(μ

j+1

− μ

This relation links the neighbor eigenvalues μ

. The shape of the potential in

this case is given by

a =

[ln(Ax + B)e

λx

]

(x + B/A)

−1

+ λ

. (6.16)

Generally the coeﬃcients in (6.14) can be complex; one recognizes the

elementary functions in the potential formula

= ξ

a(x)

′

+[ξ

a(x)+η

]

+ μ

. (6.17)

If the potential in the Schr¨odinger equation is real, it leads to some conditions

for coeﬃcients.

166 6 Applications of dressing to linear problems

Remark 6.1. There are special cases o f ψ =0andφ =0:

1. The condition ψ = 0 implies ξ

j+1

= ±ξ

. We distinguish two possibilities:

(a) ξ

j+1

= ξ

(φ = η

j+1

− η

= 0) gives a linear equation for a(x):

′

+ φa + χ =0;

hence,

a = C exp(−φx) − χ/φ.

This form corresponds to the P¨oschl–Teller potential

u = −φξ

C exp(−φx)+[ξ

C exp(−φx) − ξ

χ/φ + η

]

+ μ

. (6.18)

(b) ξ

j+1

= −ξ

results in the algebraic equation

+(ξ

j+1

− ξ

)a + η

j+1

− η

+ μ

i+1

− μ

with a constant solution.

2. The second case corresp o nds to both zero coeﬃcients φ =0andψ =0

and leads to the celebrated harmonic oscillator model a = χx;seethe

details in Sect. 4.1.

6.2 Integrable potentials in quantum mechanics

In this section we discuss exactly solvable shape-invariant potentials entering

the Schr¨odinger equation and demonstrate the usefulness of their algebraic

deformations. The Coulomb potential is treated as a typical example of the

singular shap e-invariant p otential.

6.2.1 Peculiarities

Applications in quantum mechanics impose additional conditions on trans-

formations of the potentials. The constraints are stipulated by the demand

for the potentials to b e real and to possess admissible singularities, as well

as by the speciﬁc deﬁnition of a spectrum in a Hilbert space H of solutions

of the Schr¨odinger equation . Consider ﬁrst the case of the one-dimensional

Schr¨odinger equation

−

+ U(x)ψ = Eψ (6.19)

on a line x ∈−∞, +∞ with a potential U(x)and

ψ(x, E

) ∈H

for the points E

of the discrete spectrum [324, 461], while



E+∆E

ψ(x, E

′

)dE

′

∈H

for the continuum spectrum.

6.2 Integrable potentials in quantum mechanics 167

A rigorous treatment of the DT D

for (6.19) can be given within the

assumption of the semibounded self-adjoint Hamiltonian. Let us also assume

that the potential U(x) is bounded from below [190]. As we demonstrated in

Chap. 2, the unique factorization of the operator (6.19) leads to the dressed

(partner) operator U [1] = U +2σ

, σ = φ

/φ, φ = φ(x, E

), where E

= E is

an eigenvalu e. The partner potential is nonsingular if φ is nonvanishing. The

correspondence [165] ψ → ψ[1] maps sp ectral domains of the operators H and

H[1] with the following properties:

1. Direct transformation: the auxiliary (factorization [190]) function φ is

square-integrable and the operator ∂ − σ transforms each p o int of the

discrete spectrum to a point of the discr ete spectrum excluding the low-

est on e that is removed: the corr esponding function goes to zero. The

continuum states rest on their places beca use of the same asymptotic be-

havior at inﬁnities of the eigendiﬀerential



E+∆E

ψ(x, E

′

)dE

′

[155] and

its transform



E+∆E

ψ[1](x, E

′

)dE

′

∈H.

2. Backward transformation:theinverseprop function φ(x, E

′

)

−1

′

inf

, is square-integrable (E

inf

is the inﬁnium of the spectral values of

the Hamiltonian). The prop function is a combination of independent so-

lutions φ

of (6.19), growing at opposite inﬁnities.

3. Isospectral transformation:bothφ and φ

−1

are not square-integrable;

eigenvalues E

′

asso ciated with eigenfunctions φ = φ

are out of the sp ec-

trum; the operator D

acts as an isomorphism.

Further development of the GDT consists in including transformations of

the independent var iables [190]. Following [190], we will say that H is exactly

solvable by polynomials if it is equivalent to a second-order operator that

preserves the inﬁnite ﬂag of ﬁnite-dimensional modules,

⊂ M

⊂ ...,

because of the triangl e form of the operator in such a basis. Integrability of

this kind strictly corresp onds to shap e-invariant potentials.

6.2.2 Nonsingular potentials

Shape-invariant potentials

The direct DT

u[1] = u +2(lnσ)

(6.20)

shifts the potential in a constant value C if (ln σ)

= C, which yields

σ =exp(Cx + C

or the harmonic oscillator, Morse potential, and P¨oschl–Teller potential. These

cases were mentioned in Sect. 6.1.2; see also [324]. Moreover, there are a lot

of papers whose titles begin with “On a shape-invariant ....”

168 6 Applications of dressing to linear problems

The class of shape-invariant potentials connected with the operator

P (z)

∂

∂z

+ Q(z)

∂

∂z

, (6.21)

where P and Q ar e the ﬁrst- and the second-order polynomials, corresponds to

the exactly solvable Hamiltonians that preserve the inﬁnite ﬂag of polynomial

modules

′

⊂P

⊂ ...⊂P

⊂ ..., P

=< 1,z,...,z

Rescaling x and shifting the spectrum leads to the canonical forms listed in

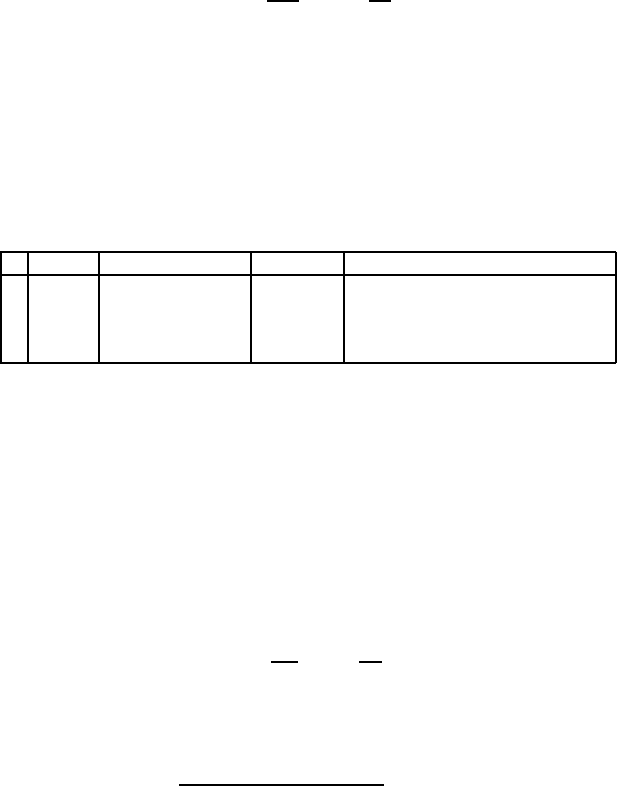
Table 6.1.

P (x) Q(x) z(x) U (x)

Ia -1 2z x x

Ib −4z 4z − 2 x

II −z

−(2A +3)z +1 exp x exp(−2x)/4 − (A +1/2) exp(−x)

III z(1 − z) (A − 3/2) + 1 − A cosh

(x/2) ( 1/4 − A

)sech

(x/2)/4

Table 6.1. Nonsingular shape-invariant potentials on the line

The Hamiltonian H is exactly solvable in polynomials if it is transformed

by a change of variable

x =



(−P )

−1/2

and a GT

φ =exp(p)f

z=z(x)

(6.22)

with

p =





Q −

′



dz (6.23)

to a Hamiltonian with a potential among those listed in Table 6.1. The trans-

formed potential goes to

U =

(Q − P

′

/2)(Q − 3 P

′

/2)

+ R|

z=z(x)

Owing to the presence of the polynomial P in the denominator, the number

and multiplicity of real roots ρ of P determine the singularity of U,ifthe

numerator is nonzero. Otherwise the potential is nonsingular, i.e., we can

formulate the following proposition:

Proposition 6.2. Let the range of z(x) be denoted as R. One of the following

possibilities holds:

1. P has no real r oots, R =(−∞, ∞),thenU has no singularities.

2. There is a double root ρ.ThenR=(−∞,ρ) or R=(ρ, ∞),andU(x) is

nonsingular.