Дипломная работа: Синтез гибридной нейронной сети для управления двухмассовой электромеханической системой с зазором. 2003 г
Подождите немного. Документ загружается.


61
Теперь мы можем записать выражение (4.7.2) в раскрытом виде:
w y
ij
n
j
n
i
n( ) ( ) ( )
1
(4.7.9)
Иногда для придания процессу коррекции весов некоторой инерционности,
сглаживающей резкие скачки при перемещении по поверхности целевой функции,
(6.7.9) дополняется значением изменения веса на предыдущей итерации
w t w t y
ij
n
ij
n
j
n
i
n( ) ( ) ( ) ( )
( ) ( ( ) ( ) )
1 1
1
(4.7.10)
где
– коэффициент инерционности, t – номер текущей итерации.
Алгоритмы сопряженных градиентов представляют собой подкласс квадратично
сходящихся методов. Они могут обучать сеть пока ее веса, входы и функции активации
имеют производные. Алгоритмы сопряженных градиентов используют градиентный
метод первого порядка для вычисления производных целевой функции относительно
весов и порогов сети [ 15 ].
Для простоты обозначим текущий градиент
w
Q
g
.
Для алгоритмов сопряженных градиентов шаг 6 обобщенного градиентного
алгоритма имеет вид:
s(w
k
)=-g
k
+
k
s(w
k-1
)
.
(4.7.11)
В большинстве алгоритмов сопряженных градиентов размер шага корректируется
при каждой итерации, в отличие от других алгоритмов, где обучающаяся скорость
используется для определения размера шага.
Различные версии алгоритмов сопряженных градиентов отличаются способом, по
которому вычисляется константа β.
Для алгоритма Флетчера-Ривса правило вычисление константы β имеет вид:
1-k
T
1-k
k
T
k
k
gg
gg
β
, (4.7.12)
где β - отношение квадрата нормы текущего градиента к квадрату нормы
предыдущего градиента [13].
В обобщенном градиентном алгоритме отсутствует процедура возврата к начальной
итерации для метода Флетчера-Ривса, но вместе с тем тесты, включенные в алгоритм,
обеспечивают обнаружение любых трудностей, ассоциированных с необходимостью
возврата при расчетах по методу сопряженных градиентов [13].
Для алгоритма Полака-Рибьера правило вычисление константы β имеет вид:
1-k
T
1-k
k
T
1-k
k
gg
gg
β
, (4.7.13)
где β - внутреннее произведение предыдущего изменения в градиенте и текущего
градиента, деленное на квадрат нормы предыдущего градиента [13].
Для обучения нейронных сетей использовалась одна из разновидностей алгоритма
обратного распространения ошибки - метод Левенберга - Маркварта. Этот метод
относится к методам Ньютона, которые являются примером способа быстрой
оптимизации обучения. Основным выражением методов Ньютона является выражение
для шага:

62
(4.7.14)
где - матрица Хессайна (содержит вторые производные градиента) на шаге при
текущем значении весов и смещений. Суть этих методов заключается в том, что на
каждом шаге приращения вычисляется аппроксимирующая матрица Хессайна, и само
приращение вычисляется как функция градиента. Этот метод более быстрый, чем
метод градиентного спуска. Однако для случая нейронных сетей прямого
распространения он требует больших вычислений.
Избежать этого позволяет применение метода Левенберга-Маркварда. Он
основан на том, что если представленная функция имеет форму суммы квадратов (как
это обычно бывает при обучении нейросетей прямого распространения), то матрицу
Хессайна можно аппроксимировать как
(4.7.15)
где градиент может быть вычислен как
(4.7.16)
где
J - Якобиан, который содержит первые производные невязок нейросети от весов и
смещений,
e - вектор невязок нейросети.
Якобиан может быть вычислен с помощью стандартной техники для метода
обратного распространения ошибки, что значительно упрощает вычисления.
Метод Левенберга - Маркварта использует аппроксимацию матрицы Хессайна
подобно приращению в методе Ньютона:
(4.7.17)
Когда скаляр равен нулю, эта формула вырождается в формулу приращения для
метода Ньютона, использующего аппроксимированную матрицу Хессайна. Когда
отлична от нуля, градиент начинает снижаться с малым шагом. Метод Левенберга -
Маркварда быстрее и точнее в районе минимума ошибки, он также стремится
увеличить скорость обучения настолько, насколько это возможно. Таким образом,
уменьшается после каждого удовлетворительного шага (уменьшение в представленной
функции) и увеличивается только тогда, когда на предварительном шаге увеличивается
минимизируемая функция. Таким образом, минимизируемая функция всегда будет
уменьшаться с каждым шагом алгоритма.
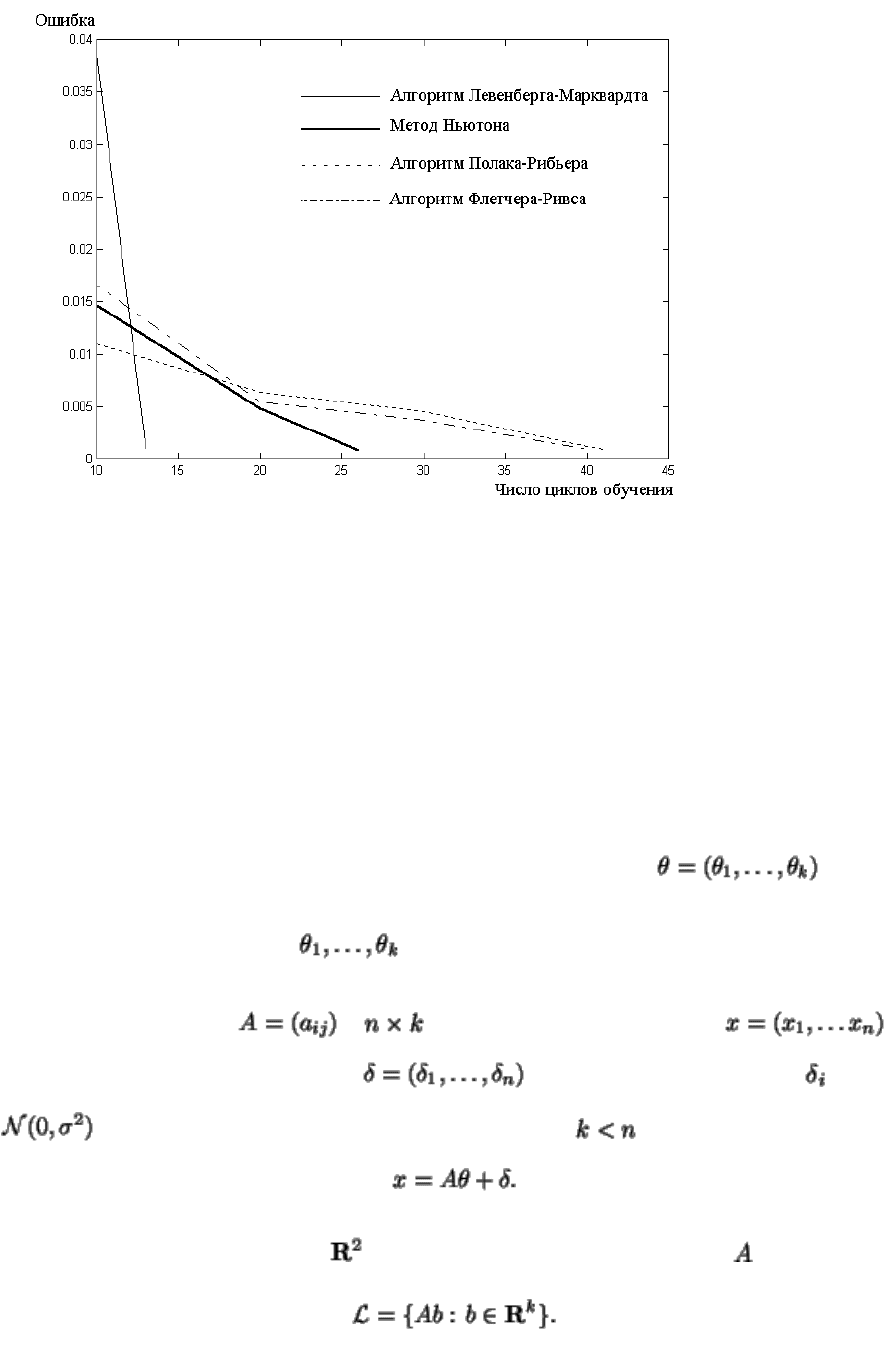
63
Рис 4.7.1. График cходимости алгоритмов обучения многослойных нейронных сетей
Метод наименьших квадратов (МНК)
Этот метод является одним из наиболее распространенных приемов статистической
обработки экспериментальных данных, относящихся к различным функциональным
зависимостям физических величин друг от друга. В том числе, он применим к
линейной зависимости и позволяет получить достоверные оценки ее параметров a и b, а
также оценить их погрешности. Рассмотрим статистическую модель эксперимента, в
котором исследуют линейную зависимость. Если градиентные алгоритмы по своей
структуре и принципу являются итерационными, МНК позволяет найти значения весов
нейрона сети за один шаг итерации.
Существует следующая модификация линейной модели. Пусть --
вектор-столбец неизвестных параметров нейрона. Предположим, что мы не можем
непосредственно наблюдать , но можем измерить их некоторые линейные
комбинации прибором, допускающим независимые случайные ошибки. Сформулируем
точную модель. Пусть -- -матрица входных сигналов, --
вектор-столбец целевых значений, -- вектор-столбец ошибок, --
. Основное предположение состоит в том, что и
Рассмотрим подпространство в , порожденное столбцами матрицы :

64
Если ввести новые параметры , то оценка должна быть
найдена из условия
следовательно, . Это равносильно тому, что для любого
, то есть , где . Пользуясь свойствами
скалярного произведения, получим
Отсюда вытекает, что
(4.7.18)
Таким образом, может быть найдено из системы линейных уравнений
именуемой системой нормальных уравнений. Если матрица имеет полный ранг, то
квадратная матрица обратима и
(4.7.19)
из выражения (4.7.19) можно вычислить все коэффициенты нейронной сети за один
шаг расчета.
Совмещая МНК для нахождения линейных параметров ANFIS сети при прямом
распространении сигнала обучающей выборки, и метод обратного распространения
ошибки при обратном распространении целевых выходов сети, мы получим так
называемый гибридный метод обучения. Он работает примерно в 10 раз быстрее чем
чистый метод обратного распространения ошибки за счет того что линейные
параметры определяются за один шаг расчета. Но в вычислительном отношении
гибридный алгоритм требует большей вычислительной мощности. Однако на практике
если позволяют вычислительные мощности, гибридный метод дает лучший результат
по скорости нахождения минимума целевой функции.
Эволюционные методы.
Можно конечно применить для обучения ГНС и Генетические алгоритмы (ГА) - это
стохастические, эвристические оптимизационные методы, впервые предложенные
Холландом (1975). Они основываются на идее эволюции с помощью естественного
отбора, выдвинутой Дарвином (1857).
К достоинсвам последнего подхода относится практически безусловное нахождение
глобального минимума целевой функции. Однако существенный аргумент против
применения ГА для задачи настройки параметров НС, это огромное вычислительное

65
время, по сравнению с градиентными методами, которые работают на два порядка
быстрее ГА, хотя и в большей степени подвержены ловушке локального минимума.
Рисунок 4.7.3. Структурная схема простейшего ГА.
В настоящее время разрабатывается множество вариантов ГА, позволяющих находить
оптимальные решения в задачах поиска минимума многомерных функций. К
преимуществам ГА можно отнести способность поиска оптимума функции, которая не
имеет строгого аналитического выражения, критичным является лишь критерий
оптимальности, позволяющий проводить селекцию, но все равно нельзя быть
полностью уверенным в том, что найденное решение является самым лучшим.

66
4.8. ПАРАМЕТРЫ ОБУЧЕННОЙ НЕЙРОННОЙ.
Для определения оптимальных параметров синтеза нейронной ANFIS сети был проведен
многофакторный эксперимент.
Качество полученной нейронной сети определяется в первую очередь видом вектора
обучения, его структурой, выбором количества и формы функций принадлежности входных
нейронов, типом нечеткого регулятора и алгоритмом обучения.
Видом вектора обучения является зависимость сигнала от времени. Структура обучающего
вектора - это дополнительные преобразования реальных данных, которые требуются для
разделения одного реального сигнала на несколько параллельных сигналов, сдвинутых на
шаг квантования. Такой прием позволяет нейронной сети повторить динамику системы, то
есть создает динамическую нейронную сеть.
Обучение проводилось в течение 60 секунд для каждого опыта, с применением
ПК : Athlon 1.5 ГГц, RAM 256 Mb , Windows2000 , Matlab6.1 R13.
INPUT ANFIS TRAIN
OUT ANFIS TRAIN
1
TL.s
1
Tfider.s
1
Tm.s
3.5
Tsum.s+1
In1
In2
Train Vector
sollen
t
M
w1
w2
Repeating
Sequence2
-K-
beta1
beta2
Clock
Рисунок 4.8 1 Структурная схема формирования обучающего множества.
Серия импульсов, представленных на рисунке 4.8.2. представляют собой набор импульсов
единичной площади. Такой формы сигнал обучения нейронной сети, наиболее приемлем с
точки зрения плотности частотного спектра, и в большей степени отвечает запросам
компактности обучающего множества и максимального качества полученного в итоге
нейронного регулятора.

67
Рисунок 4.8 2 Зависимость сигнала управления от времени, для обучения нейронной сети.
На Рисунке 4.8.3. представлена структурная схема формирования обучающего множества.
Рисунок 4.8.3.- Структурная схема формирования обучающего множества №1.
Таблица 4.8.1.- Распределение ошибки в зависимости от структуры ANFIS сети , структура
обучающего вектора №1
Число
входов
число вх
функций
функция
принадл
полная
сеть
тип
Сугено
эпохи
ошибка
Тип обучения
предел
обучения
3
2 2 2
gbellmf
да
const
1000
0.0510861
гибридный
да
3
2 2 2
gaussmf
да
const
1000
0.0595612
гибридный
нет
3
2 2 2
gbellmf
да
linear
500
0.0323542
гибридный
да
3
2 2 2
dsigmf
да
linear
50
0.0375722
гибридный
да
3
2 2 2
trimf
да
linear
10
0.044
гибридный
да
3
2 2 2
dsigmf
да
const
200
0.107474
гибридный
да
3
3 3 3
trimf
да
linear
100
0.182743
обр распр
нет
3
3 3 3
pimf
да
const
100
0.188884
гибридный
нет
3
3 3 3
gaussmf
да
linear
100
0.0185197
гибридный
нет
3
3 3 3
gauss2mf
да
linear
100
0.0228508
гибридный
нет
3
3 3 3
trimf
да
linear
100
0.025004
гибридный
нет

68
Продолжение таблицы 4.8.1. .- Распределение ошибки в зависимости от структуры ANFIS
сети , структура обучающего вектора №1
Число
входов
число вх
функций
функция
принадл
полная
сеть
тип Сугено
эпохи
ошибка
Тип
обучения
Предел
обучения
3
3 3 3
Pimf
да
linear
100
0.0336939
гибридный
нет
3
3 3 3
Trimf
да
const
100
0.04388
гибридный
да
3
3 3 3
Gaussmf
да
const
100
0.04388
гибридный
нет
3
3 3 3
Gaussmf
да
const
300
0.04389
гибридный
нет
3
3 3 3
Gaussmf
да
linear
1000
0.0899151
обр распр
нет
3
3 3 3
gauss2mf
да
const
300
0.0967972
гибридный
нет
3
4 4 4
Trimf
да
linear
100
0.0154878
гибридный
нет
3
4 4 4
Trimf
да
const
100
0.03526
гибридный
да
3
4 4 4
Trimf
да
linear
1000
0.08
обр распр
нет
3
4 4 4
Trimf
да
const
300
0.153474
обр распр
нет
3
8 8 8
Gaussmf
нет
const
100
0.0644509
обр распр
нет
3
8 8 8
Gaussmf
нет
const
1000
0.0354838
гибридный
да
3
8 8 8
gaussmf
нет
const
100
0.037765
гибридный
нет
3
8 8 8
gaussmf
нет
const
1000
0.0767027
обр распр
нет
1. Применение дифференцирующих звеньев уменьшает ошибку обучения в 2 раза.
2. функция gauss2mf имеет худшее качество обучения, чем gaussnf
3. При использовании большого числа треугольных функций принадлежности, ошибка
сети приравнивается к сетям с нелинейной функцией принадлежности.
4. Метот обратного распространения ошибки имеет такой же результат как и гибридный
метод обучения, но требует в 5 – 10 раз больше эпох обучения.
5. Системы с линейной комбинацией параметров выхода уменьшают ошибку в 2 раза, но
требуют гораздо больше времени обучения чем сети в которых параметрами вывода
являются константы.
6. Кластеризация данных резко упрощает сеть. Что позволяет обучать сеть до достижения
предела обучения, но сама ошибка остается на том же уровне. Остается неясным сам
алгоритм проведения кластеризации, что исключает использование такого подхода без
среды Матлаба.
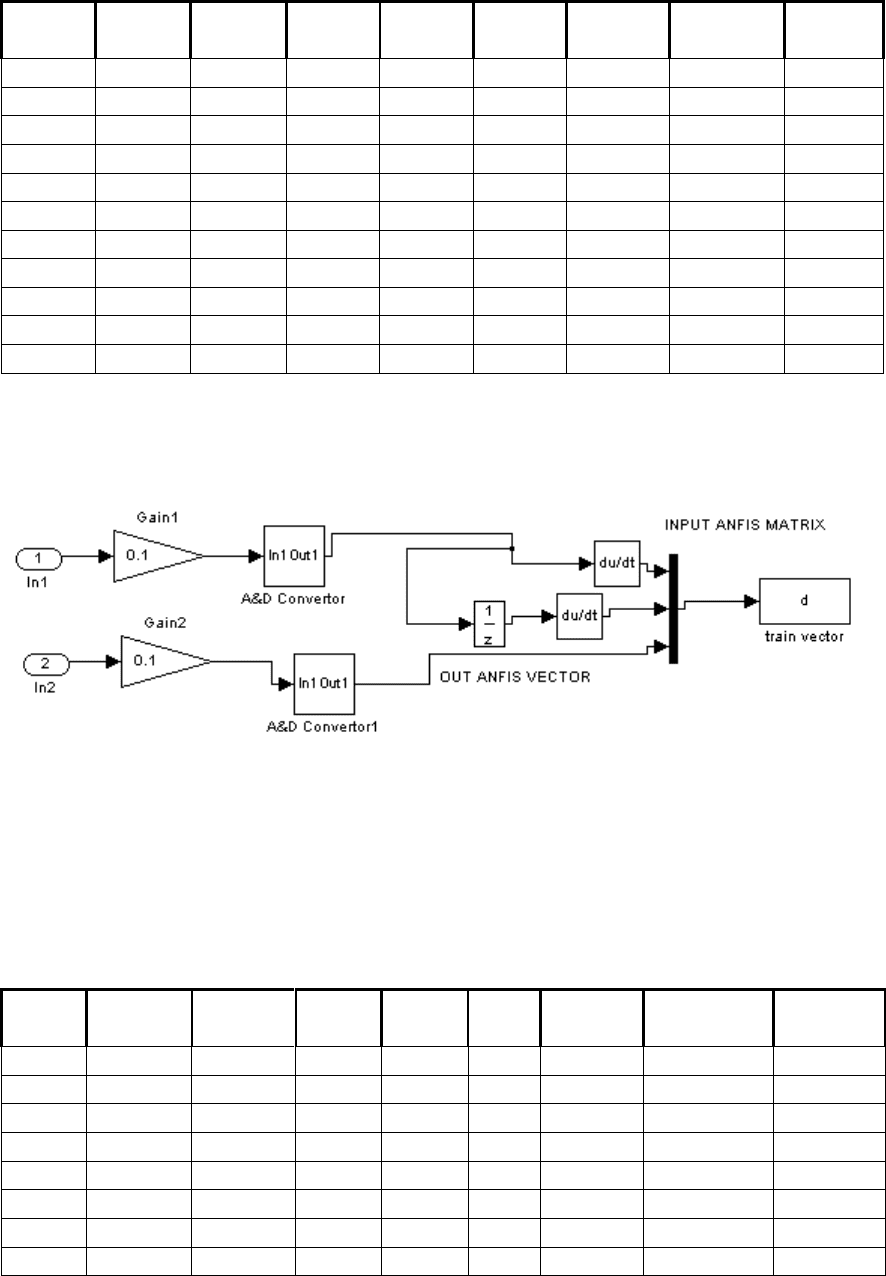
Рисунок 4.8.4.- Структурная схема формирования обучающего множества №2.
69
Таблица 4.8.2 распределение ошибки в зависимости от структуры ANFIS сети
Структура обучающего вектора № 2.
Число
входов
число вх
функций
функция
принадл
полная
сеть
тип
Сугено
Эпохи
ошибка
тип
обучения
предел
обучения
2
10 10
gaussmf
да
linear
1000
0.0886781
обр распр
нет
2
10 10
gaussmf
да
linear
10
0.0357118
гибридный
нет
2
2 2
trimf
да
const
800
0.166309
гибридный
да
2
2 2
gaussmf
да
const
560
0.230491
гибридный
нет
2
3 3
gaussmf
да
const
700
0.161054
гибридный
да
2
3 3
gaussmf
да
const
1000
0.174554
обр распр
нет
2
3 3
gaussmf
да
linear
312
0.0948254
гибридный
да
2
4 4
trimf
да
const
500
0.150849
обр распр
да
2
4 4
gaussmf
да
linear
1000
0.138458
обр распр
нет
2
4 4
trimf
да
const
120
0.151821
гибридный
да
2
5 5
gaussmf
да
linear
70
0.0537588
гибридный
да
Такая структура обучающего множества является оптимальной, так как обладает наименьшей
ошибкой при прочих равных условиях.
Рисунок 4.8. 5.- Структурная схема формирования обучающего множества №3.
Такая структура обучающего множества отличается резким увеличением ошибки
сети, а так же требует применения дифференцирования цифрового сигнала, что
усложняет физическую реализацию сети.
Таблица 4.8.3 распределение ошибки в зависимости от структуры ANFIS сети .
труктура обучающего вектора № 3.
Число
входов
число вх
функций
функция
принадл
полная
сеть
тип
Сугено
эпохи
ошибка
тип
обучения
предел
обучения
2
10 10
gaussmf
да
linear
10
0.0999
гибридный
нет
2
10 10
gaussmf
да
linear
400
0.191356
обр распр
нет
2
2 2
trimf
да
const
1000
0.1516
гибридный
нет
2
2 2
gaussmf
да
const
500
0.16
гибридный
нет
2
4 4
trimf
да
const
1000
0.1421
обр распр
нет
2
4 4
trimf
да
const
140
0.1421
гибридный
да
2
4 4
gaussmf
да
linear
1000
0.15722
обр распр
нет
2
5 5
gaussmf
да
linear
200
0.12
гибридный
да

70
Структура обучающего множества, представленная на рисунке 6 является оптимальной с
точки зрения простоты физической реализации так как имеет дифференцирования, и низкого
уровня ошибки обучения нейронной сети.
Рисунок 4.8. 6.- Структурная схема формирования обучающего множества №4.
Таблица 4.8.4 распределение ошибки в зависимости от структуры ANFIS сети.
Структура обучающего вектора № 4
Число
входов
число вх
функций
функция
принадл
полная
сеть
тип
Сугено
эпохи
ошибка
тип
обучения
предел
обучения
2
10 10
gaussmf
да
linear
10
0.0602
гибридный
нет
2
10 10
gaussmf
да
const
100
0.0807
гибридный
да
2
3 3
gaussmf
да
linear
200
0.1037
гибридный
да
2
3 3
gaussmf
да
const
200
0.17
гибридный
да
2
5 5
trimf
да
const
200
0.1572
гибридный
да
2
5 5
trapmf
да
const
200
0.1674
гибридный
да
Применение трапецеидальных термов не приводит к улучшению обучения, по сравнению с
треугольными термами.
Функция принадлежности формы колокола приводит к быстрому достижению предела
обучения, в то время как функция Гаусса продолжает медленно уменьшаться до уровня
ошибки с функцией колокола
В пакете Matlab 6.1. параметры представляются в виде файла. Начальные и конечные
параметры нейронной сети, представлены в приложении В.
