Дипломная работа: Синтез гибридной нейронной сети для управления двухмассовой электромеханической системой с зазором. 2003 г
Подождите немного. Документ загружается.

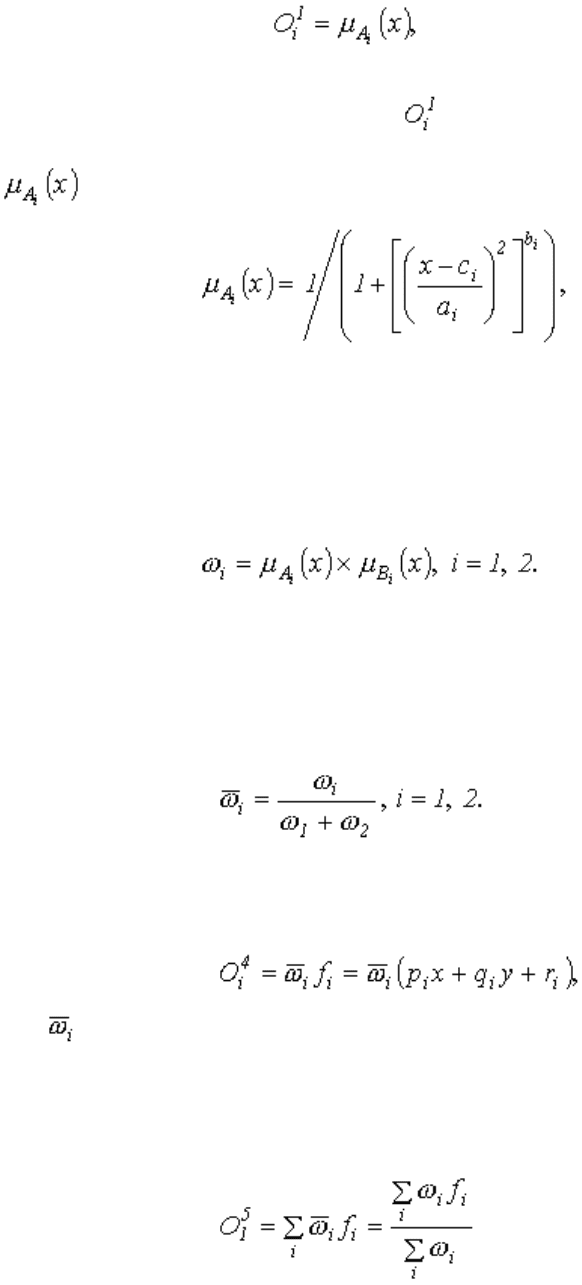
41
1-й слой: производит распределение сигналов по слою функций принадлежности, на
каждый вход.
2-й слой: Каждый узел данного слоя является адаптивным узлом со следующей
узловой функцией:
(4.3.5)
где x - входной сигнал узла i, A
i
- лингвистическая переменная, связанная с данной
узловой функцией. Другими словами, - функция принадлежности переменной A
i
,
определяющей степень, с которой данный x удовлетворяет A
i
. Обычно, в качестве
выбирается колоколообразная функция:
(4.3.6)
где {a
i
, b
i
, c
i
} - набор параметров данного слоя. Параметры этого слоя относятся к так
называемым параметрам предпосылок. Хотя, на ее место можно поставить любую
дифференцируемую функцию в диапазоне изменения входного сигнала.
3-й слой: Каждый узел данного слоя является фиксированным узлом, перемножающим
входные сигналы, причем выходное значение узла представляет собой вес некоторого
правила:
(4.3.7)
В принципе может быть использована другая подобная функция вычисления
логического «И», например поиск минимума.
4-й слой: Каждый i-ый узел данного слоя определяет отношение веса i-го правила к
сумме весов всех правил, то есть производит нормализацию сигнала отдельного
правила:
(4.3.8)
Выходные сигналы 4-го слоя называются нормализованными весами.
5-й слой: Узлы данного слоя определяются линейными (для модели типа Сугено
первого порядка) функциями принадлежности выходных переменных:
(4.3.9)
где - выходной сигнал 4-го слоя и {p
i
, q
i
, r
i
} - набор параметров данного слоя (так
называемые параметры вывода).
6-й слой: Единственный узел данного слоя является фиксированным узлом, в котором
вычисляется полное выходное значение адаптивной сети как сумма всех входных
сигналов:
(4.3.10)
42
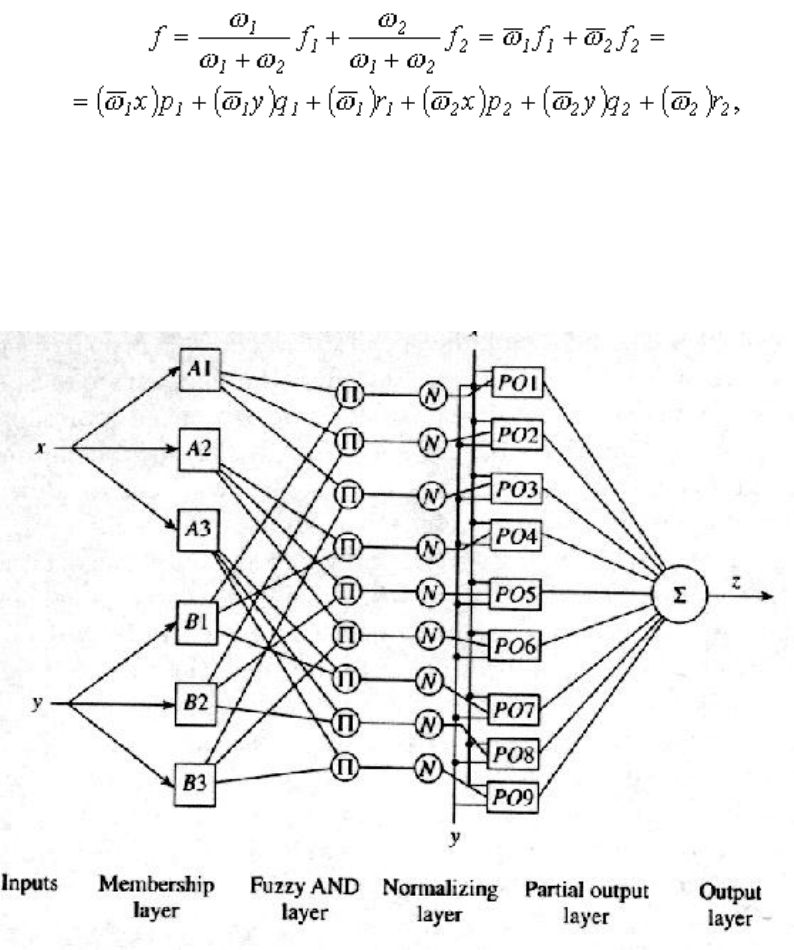
Очевидно, что для заданных значений параметров предпосылок, полное выходное
значение (рис. 4) является линейной комбинацией параметров вывода:
(4.3.11)
где p
1
, q
1
, r
1
, p
2
, q
2
, r
2
- параметры вывода. Таким образом, алгоритм гибридного
обучения, описанный выше, может быть без изменений применен к системам нечетких
рассуждений Сугено. Во время прямого прохода определяются параметров вывода
методом наименьших квадратов. Во время обратного прохода обновляются параметры
предпосылок с помощью метода снижения градиента от функционала ошибки
обучения.
Рисунок 4.3. 10 нейро фаззи сеть ANFIS архитектуры, состоящая из 6 слоев.
На рисунке 4.3.10 изображена адаптивная нейрофаззи сеть, которая может быть
рассчитана и смоделирована пакетом Матлаб 6.1. другие архитектуры гибридных
нейронных сетей в этом пакете пока не реализованы.
43
4.4. ПРИНЦИПИАЛЬНАЯ СХЕМА ПРИМЕНЕНИЯ НЕЙРОННОЙ СЕТИ.
Для управления нелинейным объектом регулирования могут использоваться несколько
альтернативных подходов к построению структурной схемы системы при обучении и с
различным местом нейронной сети в управляемой системе.
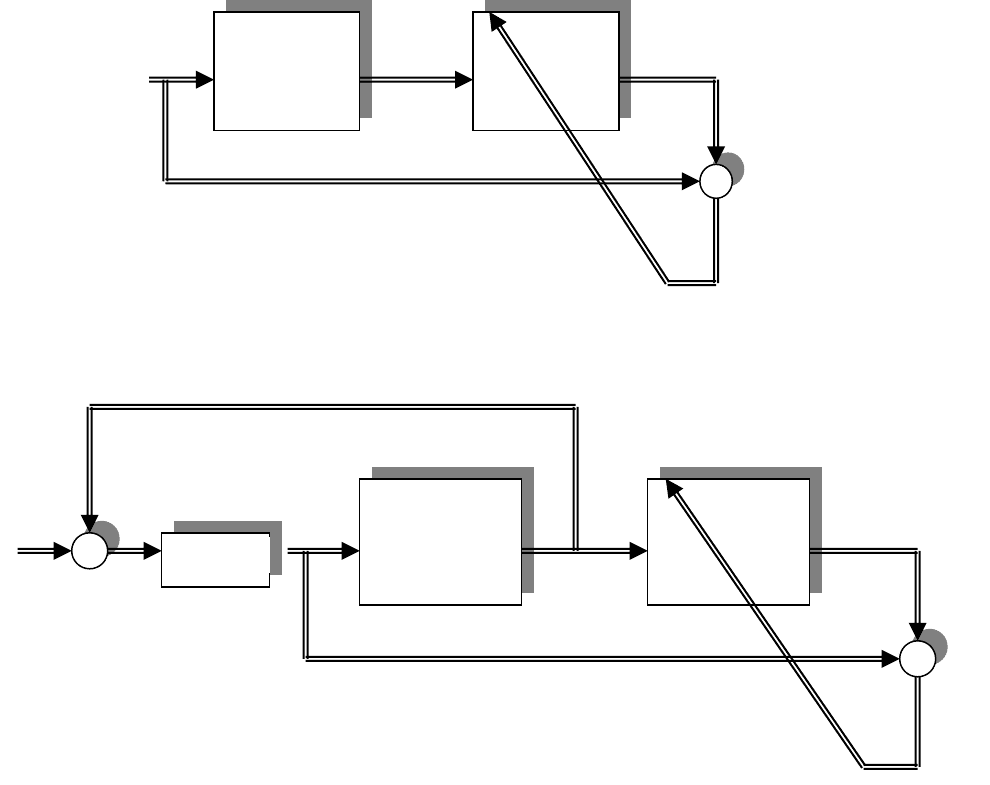
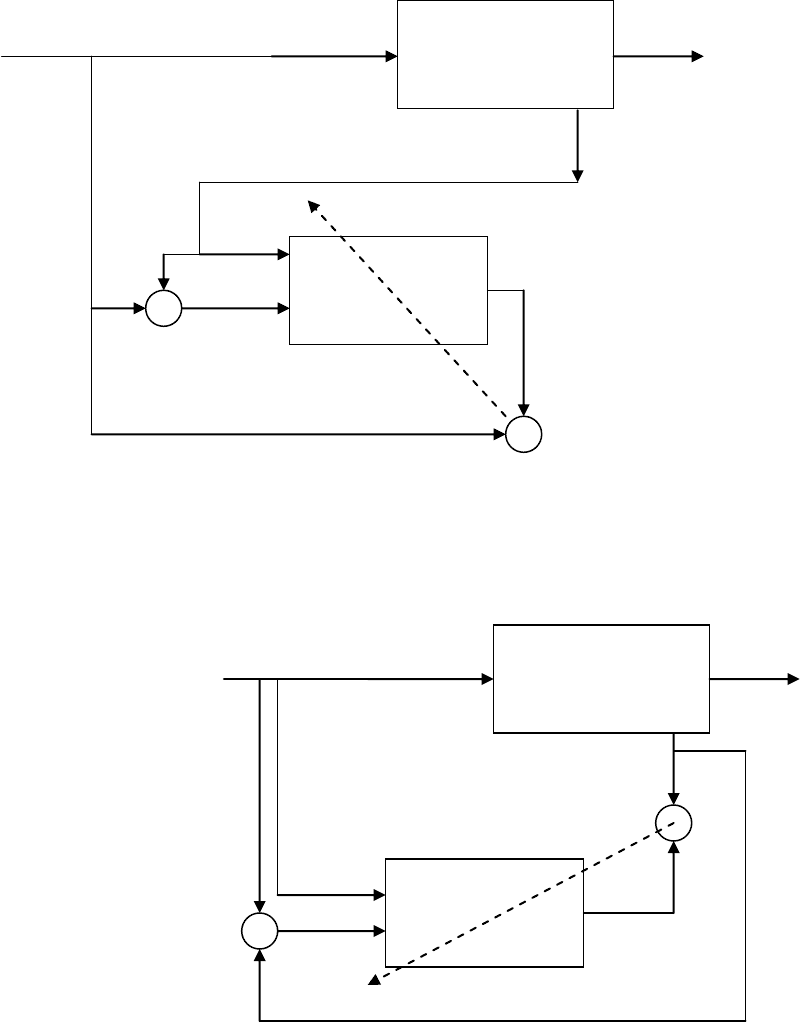
Рисунок 4.4.1. Структурная схема с архитектурой инверсного контроля. Тренировка с
открытым контуром.
Рисунок 4.4.2. Структурная схема с архитектурой инверсного контроля. Тренировка с
замкнутым контуром регулирования.
В случае тренировки сети по схеме, изображенной на рисунке 6.4.1. нейроконтроллер
NC будет представлять собой инверсную модель объекта управления и постановка
инверсной модели в прямой контур управления с обратной связью. Такой подход
приводит к компенсации передаточной функции объекта, а произведение
передаточной функции регулятора и объекта должно быть равно единице.
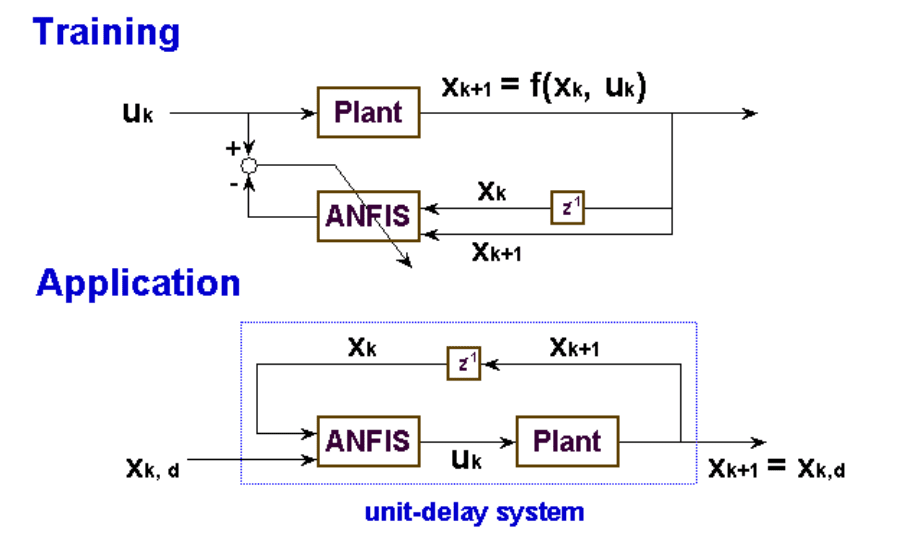
На рисунке 6.4.3 этот случай проиллюстрирован на примере ANFIS сети. Именно
этот способ обучения и использования нейронной сети применяется в данной работе.
Добавление линий задержки необходимо чтобы статическая по своей природе
гибридная нейронная сеть получила способность к аппроксимации динамической
функции. Поскольку объект регулирования имеет в своей структуре интеграторы, это
--
+
PLANT
F(u)
NC
u
E
u
--
+
PLANT
F(u)
NC
E
--
PI-R
44
приводит к задержке сигнала при прохождении внутри объекта. Применение цифровых
задержек является аппроксимацией реальных непрерывных переходных процессов.
Причем, для адекватной работы статической нейронной сети количество линий
задержки должно быть равно количеству интеграторов в системе.
Однако это не единственный вариант.
На рисунке 4.4.2. представлена структурная схема в которой нейронный регулятор
после обучения будет повторять ПИ – регулятор.
Рисунок 4.4.3. Структурная схема создания инверсной модели объекта.
На самом деле с помощью нейронной сети, в данном случае с помощью гибридной
нейронной сети, можно заменить практически любой непрерывный регулятор,
рассчитанный аналитическим путем, поскольку для НС необходимым условием
является лишь формирование обучающего множества, на котором формируются
параметры НС.
Хотя представленные схемы отличает максимальная простота, иногда лучший
результат можно получить с использованием более сложных вариантов построения
системы обучения нейронной сети [6].В таких схемах часто используется несколько
нейронных сетей одновременно, одна для идентификации объекта регулирования,
вторая, как регулятор.
Для повышения точности аппроксимации динамического объекта применяется неро
фаззи идентификатор использующий разностный сигнал текущей и заданной скорости
двигателя.
На рисунке 4.4.4. представлена схема обучения такой системы, в качестве обратной
модели объекта.
Прямая модель – это нейронная сеть, которая повторяет переходной процесс объекта
регулирования, являясь своего рода наблюдателем системы.
Инверсная модель – это нейронная сеть, которая восстанавливает входной сигнал
объекта регулирования, при известном выходном сигнале.
На рисунке 4.4.5 представлена принципиальная схема тренировки прямой модели
объекта.
45
U - n_soll las
mot
-
+
-
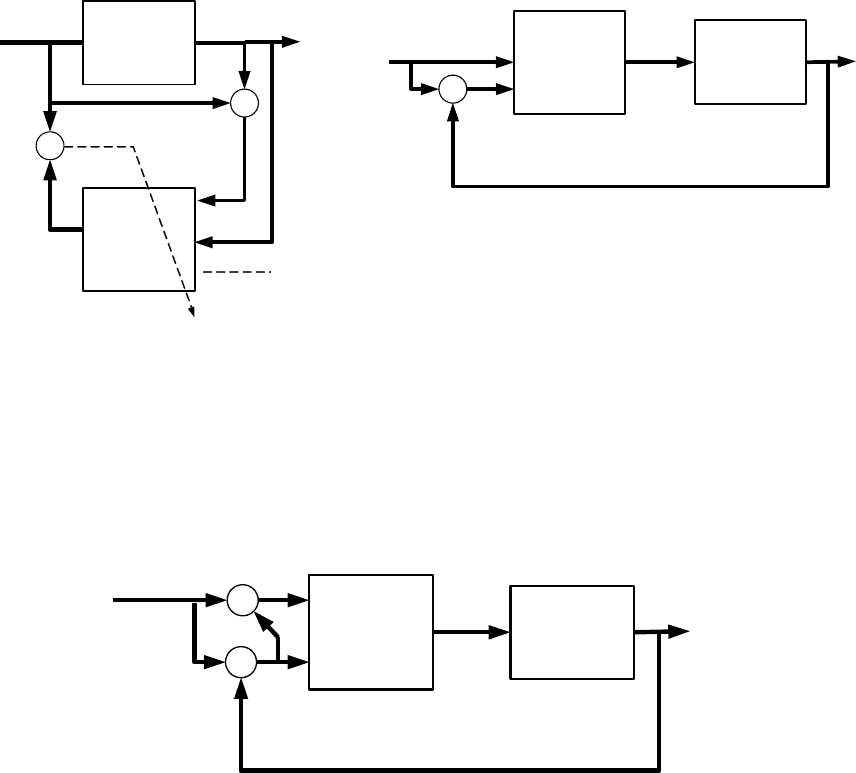
Рисунок 4.4.4.Принципиальная схема обучения нейронных сетей для инверсной
модели объекта.
U - n_soll last
mot
-
+ nn
-
Рисунок 4.4.5 Принципиальная схема обучения нейронных сетей для прямой модели
объекта.
Двухмассовый
нелинейный
электропривод
Нейронная сеть
ANFIS
Inverse Model
Двухмассовый
нелинейный
электропривод
Нейронная сеть
ANFIS
Direct Model
46
Полученные прямая и инверсная модель объекта управления используются для
построения системы управления нелинейными динамическими системами.
Простейшим вариантом будет применение инверсной модели как регулятора в прямом
канале, по принципу прямого инверсного управления. Суть этого принципа
управления сводится к компенсации нелинейности системы, с помощью нелинейной
обратной модели системы, выполненной на принципах нейронной сети. Но поскольку
нейро сети не могут полностью идеально повторить непрерывную динамическую
систему, то и сам принцип управления не выполняется строго математически.
Объект
2 массовый ЭП с
зазором
Нейронная
сеть
ANFIS
Uy
-
e
-
-
Фаза обучения нейронной сети, с сумматором на
входе, как обратной модели объекта
Объект
2 массовый ЭП с
зазором
Нейронная
сеть
ANFIS
Обратная модель
объекта регулирования
Фаза применения нейронной сети с сумматором на входе,
работающей как обратная модель
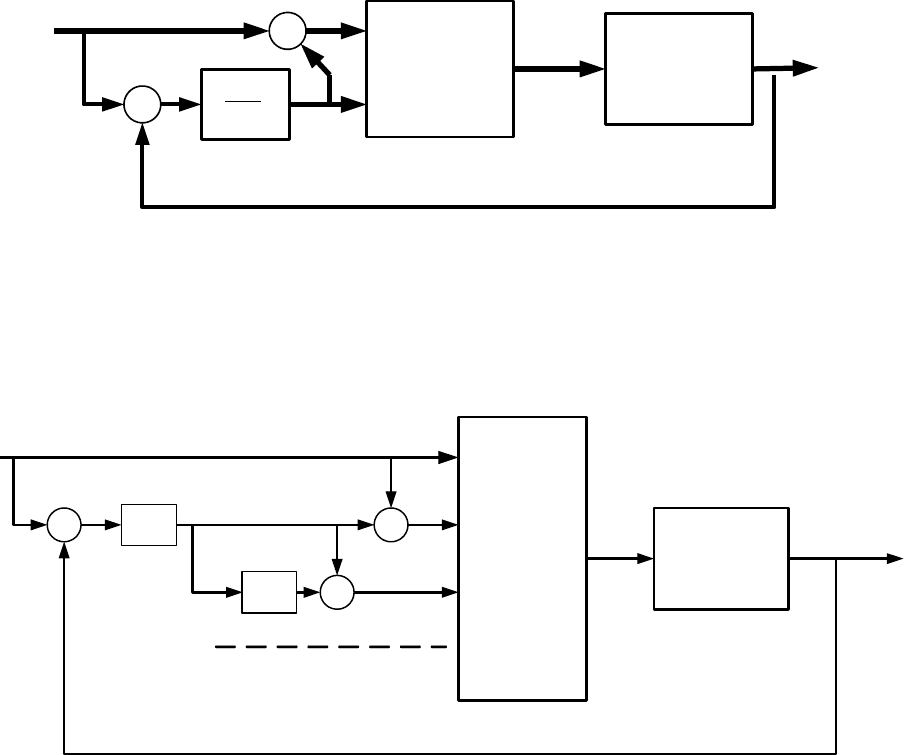
Рисунок 4.4.6. принцип прямого инверсного управления с использованием сигнала
рассогласования скорости
Однако, такие системы не могут обеспечить астатизм по управляющему и
возмущающему сигналу, следующим шагом является коррекция управляющего сигнала
на величину, пропорциональную отклонению. Принципиальная схема такого
регулятора представлена на рисунке 4.4.7.
Объект
2 массовый ЭП
с зазором
Нейронная
сеть
ANFIS
Обратная модель
объекта регулирования
Фаза применения нейронной сети с сумматором на входе,
работающей как обратная модель. Добавлена коррекция
управляющего сигнала.
Uy
-
-
Рисунок 4.4.7 принципиальная схема.
И все таки даже корректирование в канале управления не гарантирует получение
астатизма.
Наша сеть имеет на входе сигнал рассогласования скоростей, заданной и фактической,
логично, что интегрирование этого сигнала приведет всю систему к астатизму, точно
так же как это происходит при введении пропорционально интегрального регулятора
скорости или тока.
47
Объект
2 массовый ЭП
с зазором
Нейронная
сеть
ANFIS
Обратная модель
объекта регулирования
Uy
-
-
pTu
1
Рисунок 4.4.8. Принципиальная схема с коррекцией скорости и интегратором.
Так же как использование задержанных сигналов способствует аппроксимации
динамического объекта с помощью без инерционной сети, так и вычисление
производных первого и второго порядка от скорости так же приводит к улучшению
переходных процессов, устранению колебаний и линеаризации электромеханической
системы.
Объект
2 массовый ЭП
с зазором
Нейронная
сеть
ANFIS
Обратная модель
объекта регулирования
1
Z
1
Z
-
-
-
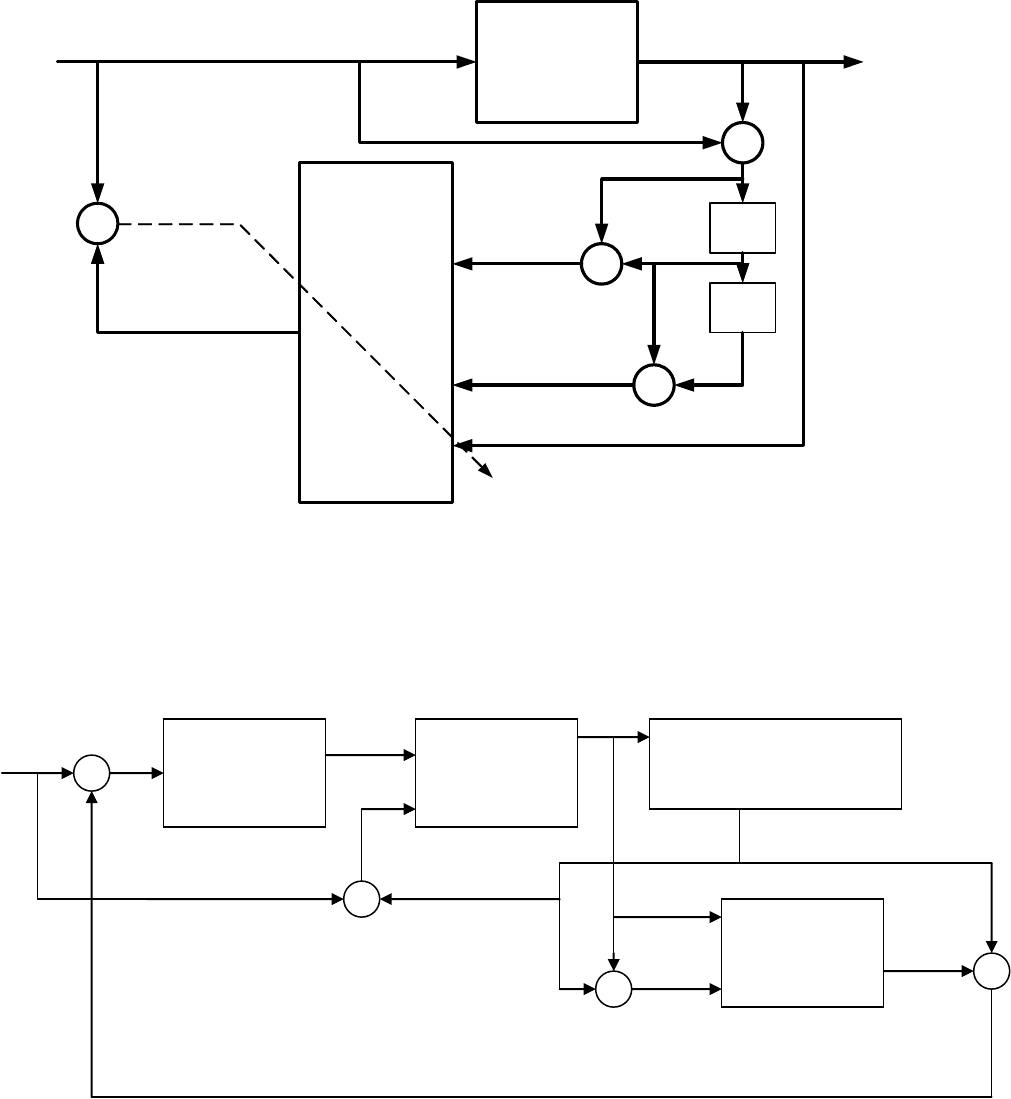
Рисунок 4.4.9 Структурная схема в рабочей фазе на основе вычисляемых разностей
задержанных сигналов.
Как мы знаем, производная от дискретной функции на данном участке может быть
вычислена как разность текущего значения измеряемой величины и ее предыдущего
значения. Это вычисление и повторяется с помощью сумматоров, стоящих перед
входом сети. Сумматор, Вычисляющий разность текущего и заданного значения
скорости необходим, чтобы, как и в ранее рассмотренных схемах, уменьшить ошибку
обучения, и дать возможность для применения интегратора. Хотя, физический смысл
производных в данном случае не очевиден, на графиках переходных процессов, мы
увидим, что такая система работает лучше, чем система с использованием тольно
задержек или только сигнала рассогласования, или комбинированная система с
задержками и вычислением рассогласования скорости.
На рисунке 4.4.10 представлена принципиальная схема в фазе обучения, для системы с
вычислением производных.
48
Цифровой
фильтр
Инверсная
АNFIS
модель
ОБЪЕКТ
РЕГУЛИРОВАНИЯ
Прямая
АNFIS
модель
Объект
2 массовый ЭП
с зазором
Нейронная
сеть
ANFIS
1
Z
1
Z
Uy
e
-
-
-
-
Рисунок 4.4.10 Принципиальная схема обучения сети с вычислением производных.
Еще одним вариантом построения системы управления можно считать схему с
применением прямой и обратной модели регулируемой системы. Принцип
формирования прямой и обратной(инверсной) модели приведен на рисунках 4.4.4 и
4.4.5.
U
+
+
+ -
-
+ +
-
Рисунок 4.4.11 Принцип применения прямой и обратной сети ANFIS для управления.
Данная схема полностью синтезируется с помощью алгоритма обучения сети.
Цифровой фильтр в схеме применяется для подавления колебаний, возникающих при
сравнении реального значения скорости и восстановленного прямой моделью, которая
выполняет роль наблюдателя состояния, однако не является им, в полном понимании,
поскольку является всего лишь приближением к нему, и работает в ограниченном
диапазоне значений входных координат. Сохраняя идеологию прямого инверсного
управления, обратная модель системы ставится в прямой канал регулирования. В
процессе работы на реальную систему действует момент сопротивления, и при
49
сравнении сигналов прямой модели и реального значения скорости, мы получим сигнал
рассогласования, пропорциональный ошибке регулирования, именно этот сигнал
является корректирующим для системы, и путем увеличения задающего сигнала на
нужную величину позволяет избавиться от статической ошибки по управлению и
возмущению.
Подбор обучающего вектора.
Характер изменения обучающего вектора, который будет подаваться на
реальную установку с целью формирования обучающего множества для нейронной
сети должен удовлетворять двум противоречивым требованиям. С одной стороны такой
вектор должен иметь простую форму, для синтеза с помощью задающего устройства –
контроллера, или DSP карты, и не приводить к повреждению самого привода и
элементов механики. С другой стороны выступают теоретические требования, для
улучшения характеристик обучения нейронной сети и создания адекватной модели
динамического нелинейного объекта управления.
Таким образом, реальный вектор обучения представляет собой компромисс
между этими позициями. Для получения максимального качества обучения требуется
подать сигнал, обладающий широким частотным спектром, для того чтобы научить
сеть реагировать на возможные вариации входного вектора. Наиболее простыми
являются ступенчатые сигналы различной формы. Идеальным для формирования
обучающего множества был бы импульсный сигнал бесконечной амплитуды и
бесконечно малой продолжительности времени, так чтобы интеграл
1)(
0
thJ
(4.4.1)
Однако на практике величина сигнала ограничена на уровне 10 вольт, а время
изменения функции не может быть меньше шага квантования в системе управления.
Разложение в ряд Фурье проводилось с помощью функции разложения
временных сигналов в спектр. При этом выполнялась ниже следующая программа:
%furie pribrazovanie dla vectora vchoda pri obuchenii file resurs : probinv.mdl
%Tsepkovsky Yuriy Jan 2003
M=size(Uz);
M=M(1);
A=abs(fft(Uz))/M;
% nachalo : 1/ T rasch : 1/step
f=0:1/0.25:1/0.0001; % f=f';
% freguence spectr
figure(3);plot(f,A);zoom; grid on;
set(gca,'xscale','lin','yscale','log');
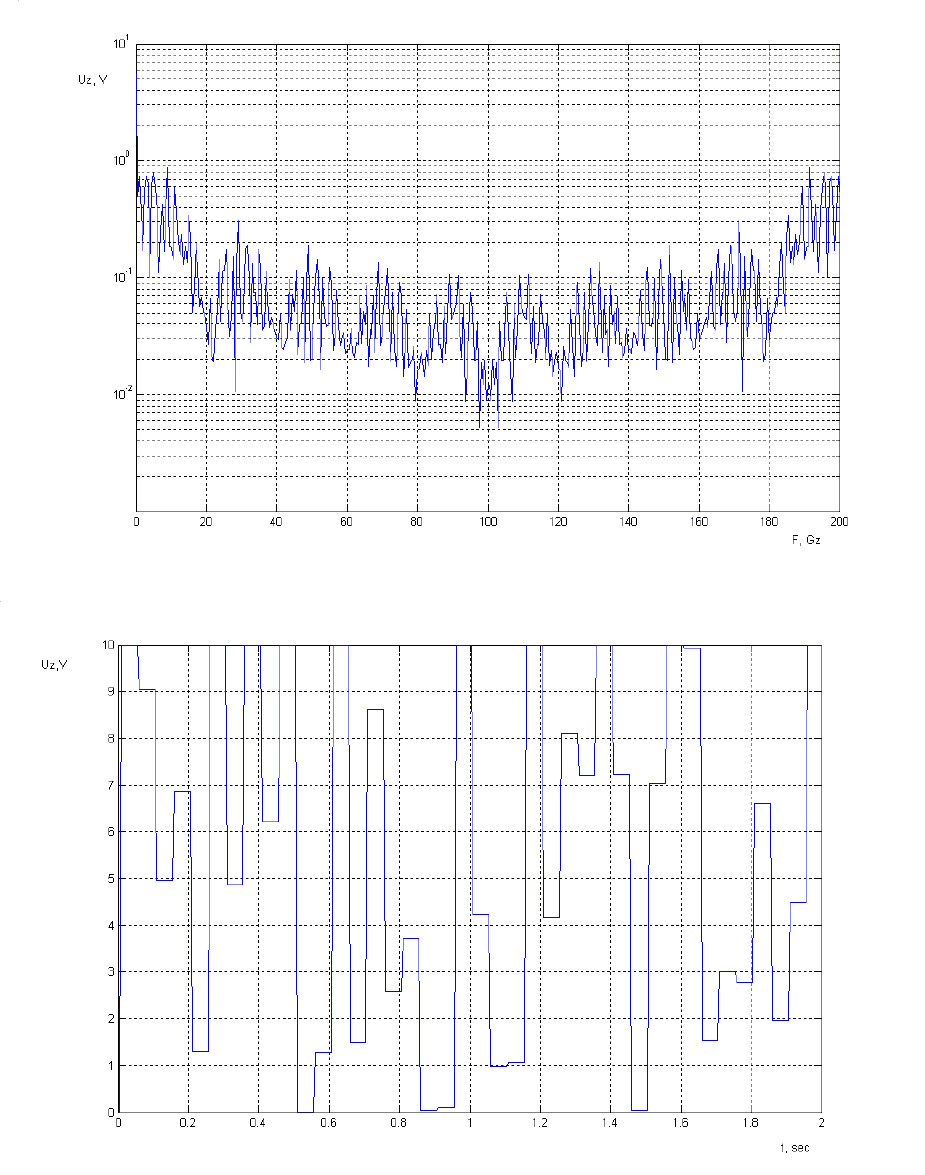
50
Рисунок 4.4.4.- Частотный спектр случайного сигнала ступенчатой формы.
Рисунок 4.4.5.- Вид случайного ступенчатого сигнала. Ширина ступеньки 0.05сек.
Создание такого сигнала требует генератора случайных чисел, создание задержек.
Однако это не приводит к заметному расширению спектра сигнала.
