Dionne G.F. Magnetic Oxides

Подождите немного. Документ загружается.

70 2 Magnetic Ions in Oxides





.1/



.2/



.1/ d

.2/

D F

 2F

 4F

.Slater integrals/ (2.31a)

D A  2B C C.Racah parameters/;





.1/



.2/



.1/ d

.2/

D 3F

C 20F

.Slater integrals/ (2.31b)

D 3B C C.Racah parameters/:

From combinations of these integrals together with the help of group theory, the

“promotional” energies are computed and added to the octahedral energies already

determined from the respective electron distribution of the particular state to com-

plete the energy term diagram. The F

parameters are the Slater integrals of the

various d orbital functions expressed in their basic spherical harmonics. Their iden-

tities have been documented in the original work [26]. Alternatively, Racah [27]

deﬁned parameters A, B,andC that can be reduced to the Slater integrals. In tab-

ular form, these interaction energies and related term information of the d

case

are listed in Table2.8 for the strong-ﬁeld method [7]. The evolution from the term

diagram to the weak ﬁeld result is sketched in Fig. 2.16. For additional comparison

with the listings in Table 2.8, the term energies from the weak ﬁeld approach are

presented in Table 2.9.

The strong ﬁeld approach to crystal ﬁeld theory will be revisited in our discussion

of S-state ion magnetoelastic properties in Chap. 5 and in the general discussion of

electric dipole optical transitions for Faraday rotation in the magnetic garnets in

Chap. 7. For future reference, the Racah parameter relations for the lowest ﬁve d

terms listed in Table 2.4 are recorded in Table 2.10. In most situations, however, a

simpler approximation based on the ground state stabilization energies is all that is

necessary to sort out the causes of the various magnetic properties.

Table 2.8 d

Term splittings for strong ﬁeld octahedral coordination

Free-ion term E

rep

Crystal-ﬁeld term E

S A C 14B C 7C

G A C 4B C 2C

C 4Dq

C 4=7Dq

C 2Dq

– 26=7Dq

P A C 7B

D A – 3B C 2C

C 24=7Dq

– 16=7Dq

F A – 8B

C 12Dq

C 2Dq

6Dq

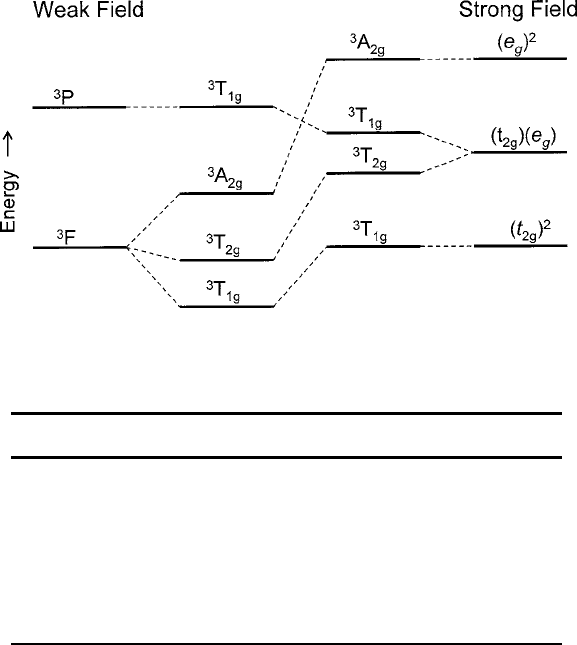
2.3 Crystal Electric Fields 71

Fig. 2.16 Schematic of energy levels of a d

ion in an octahedral crystal ﬁeld of increasing

strength

Table 2.9 d

Term energies for weak ﬁeld octahedral coordination

Crystal-ﬁeld

conﬁguration

cryst

Crystal-ﬁeld term E

term





C12Dq

A C 8B C 4C

A C 2C

A – 8B









C2Dq

A C 4B C 2C

A C 2C

A C 4B

A – 8B





–8Dq

2.3.7 Rare-Earth Ion Solutions

Crystal-ﬁeld stabilizations of the orbital angular momentum must be treated

differently in the rare-earth 4f

series because H

>>V

, which means that

J is the quantum number that deﬁnes the angular momentum. Because of the

stronger œLS energy, the terms are ﬁrst split into a multiplet of states with J

values running from

L S

L C S

in the standard notation of atomic spec-

tra. As a consequence the term splittings caused by the crystal ﬁeld are labeled

according to the J instead of the L degeneracies (although in the physical reality

only L is quenched). Nonetheless, effects of the crystal ﬁeld are signiﬁcant in

magnetic properties of oxides, and the various term splittings established with the

aid of group theory and operator equivalents as determined by Lea et al. [28]are

summarized in Table 2.11. These eigenstates of the crystal ﬁeld represent raising

of the J degeneracy and therefore can cause a decrease in the effective J value as

72 2 Magnetic Ions in Oxides

Table 2.10 Racah parameter energy relations for d

and d

10n

with

n D 2,3,4, and 5

S D A C14B C 7C

F D 3A C 9B C 3C

D D A – B C 2C

G D 3A – 11B C 3C

G D A C 4B C 2C

H D

P D 3A – 6B C 3C

P D A C7B

P D 3A

F D A – 8B

F D 3A – 15B





D D 6A – 5B C 4C

F D 10A – 13B C 7C

F D 6A – 5B C

11=2

D D 10A – 18B C 5C

3=2



68B

C 4BC C C



1=2

G D 6A – 12B C 4C

P D 10A – 28B C 7C

H D 6A – 17B C 4C

G D 10A – 25B C 5C

D D 6A21B

S D 10A – 35B

The derivation of these relations can be found in [5], Sect. 4.6

These terms are listed differently from that anticipated by Hund’s

rule in that the

Pand

F terms are exchanged in position on the

energy ladder. This is an artifact of this conﬁguration and results for

the relative values of B and C , which are found to occur in the ratio of

C=B4:5. There are other departures from the Hund’s rule norm that

will be fall beyond the scope of this discussion

Table 2.11 4f

(Rare-earth

group) term splittings in an

oxygen coordination of O

symmetry

J Term representations

1/2 E

1=2g

1 T

3/2 G

2 E C T

5/2 E

5=2g

C G

3 A

C T

7/2 E

1=2g

C E

5=2g

C G

4 A

C E

C T

9/2 E

1=2g

C 2G

5 E

C 2T

C T

11/2 E

1=2g

C E

5=2g

C 2G

6 A

C A

C E

C T

C2T

13/2 E

1=2g

C 2E

5=2g

C 2G

7 A

C E

C 2T

15/2 E

1=2g

C E

5=2g

C 3G

8 A

C 2E

C 2T

The contents of this table are included

here because they cover the full scope of

the 4f

series that is important in the

context of this book. In addition, these

entries could also the ﬁrst complete listing

available in the public domain

2.4 Orbital Energy Stabilization 73

measured magnetically, just as in the case of orbital angular momentum quenching

of L in the d

series.

The situation regarding the rare-earth ions becomes more complex not only be-

cause the high J multiplicities render analytical solutions more laborious, but also

because magnetic exchange ﬁelds interact only with the spin component of J .More-

over, since the crystal ﬁeld is about two orders of magnitude smaller than that of

the d

series, the degree of J quenching can been inﬂuenced by externally ap-

plied magnetic ﬁelds of magnitudes (>10T) that are now attainable with modern

magnet technology, for example, superconducting magnets. These effects of com-

peting crystal ﬁelds, exchange ﬁelds, and applied magnetic ﬁelds are examined in

the context of the magnetic properties of the rare-earth iron garnets in Sect. 4.3.3,

and later in relation to electron spin resonance in Chap. 6.

2.4 Orbital Energy Stabilization

When cations are placed in a lattice, the crystal ﬁeld from the anion charges is

derived from the ionic part of the chemical bonding. As a consequence, the spin

occupancies pictured in Fig. 2.3 for free ions will undergo modiﬁcations. Within

the point charge approximation, the resultant electrostatic potential between neigh-

boring ions (often approximated by a lattice energy calculation) and the ionization

potentials of the various ionic species determine the electronic energies of the

outermost electrons. For the 3d

-electron series, the local crystal ﬁeld of the imme-

diate anion neighbors provides additional binding energy by lowering the electronic

ground state energy as part of the splitting of the orbital degeneracy that was re-

viewed in the previous section. The additional electronic stabilization is therefore

the result of a perturbation by the point-charge ﬁeld, which may be further enhanced

by a covalent interaction.

2.4.1 One-Electron Model

In the weak-ﬁeld regime, a one-electron model can be constructed for the 3d

series

as a general qualitative approximation to provide an occupancy map of the ground

state electronic structures sketched. Instead of computing the electron interaction

energies in terms of the Slater integrals or Racah parameters, the ground state is ﬁrst

pictured as a distribution of electrons among the cubic ﬁeld terms [29]. The energy

levels of the T

and E

terms from the

Dand

D cases of Fig. 2.12 for single-d

electron are used as a “ﬂoor plan” to keep track of the likely d -electron spin dis-

tributions in the ground states, as diagrammed in Figs. 2.17 and 2.18 for octahedral

and tetrahedral coordinations, respectively, including the low-spin states that can

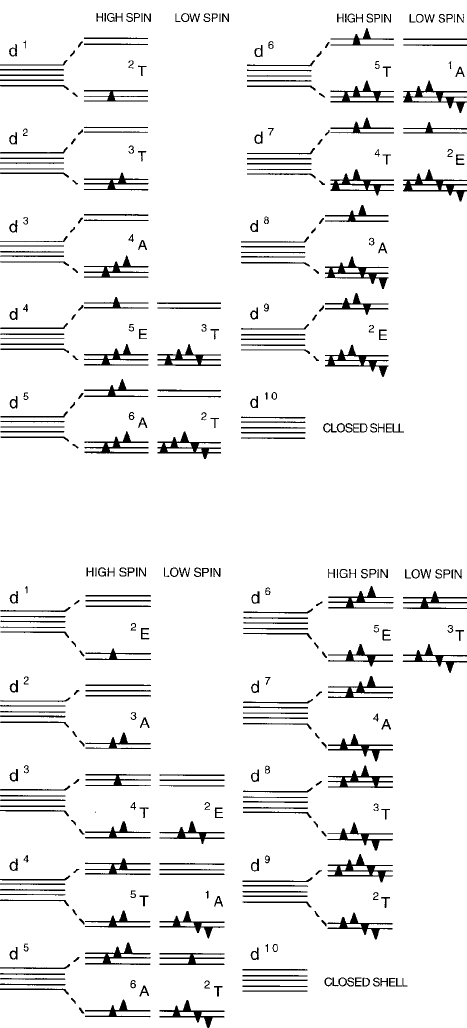
74 2 Magnetic Ions in Oxides

Fig. 2.17 One-electron d -orbital occupancy diagrams: octahedral site

Fig. 2.18 One-electron d -orbital occupancy diagrams: tetrahedral site

2.4 Orbital Energy Stabilization 75

occur in strong crystal ﬁelds (violation of Hund’s rule).

In this abbreviation, the

“Aufbau method” is applied by adding d electrons sequentially beginning with the

orbital state of lowest energy, while observing Hund’s rule of spin polarization for

the ﬁrst (’)halfofthed shell and the Pauli principle of spin pairing as spins are

added to the second (“)half.

Although not shown explicitly, the crystal-ﬁeld stabilization energy of each

conﬁguration is offset by intraorbital electron repulsion energy e

,whichis

manifested by the particular ionization potential (IP) in Fig. 2.19a (replotted from

Fig. 2.8 for 2Cand 3C) as a function of n across the transition series.

Note that the

destabilization energy (characterized by the parameter U

)of“ spins relative to ’

spins in the same orbital is on the order of 2–3 eV, which exceeds the 10Dq values

of many oxide sites.

It is appropriate here to point out that the Aufbau approximation can apply with

rigor to only the d

or d

cases. For that reason, the model is often called the “one-

electron approximation.” Where the effects of intraelectron repulsion must be taken

into account, multielectron solutions with their attendant complexities in dealing

with other important perturbations such as spin–orbit coupling, magnetic exchange,

and Zeeman effects in an external magnetic ﬁeld can be considered.

2.4.2 High- and Low-Spin States

Where H

Hund

exceeds H

, this procedure establishes a ground state with the max-

imum available spin number. The electrons are distributed among the orbital states

with Pauli spin pairing permitted only after each of the ﬁve orbitals are half-ﬁlled

(Hund’s rule). Since the energy distribution also changes with the assignment of

electrons, one of the main insights gained from this approximation is the relative

magnitudes of the cation site stabilization energies. In Figs. 2.17 and 2.18, the one-

electron ground-state conﬁgurations for the octahedral and tetrahedral sites include

The Aufbau concept can be used here directly because all of the electrons occupy orthogonal

crystal-ﬁeld states of the same orbital term under the inﬂuence of the same nuclear charge. When

applied to molecular bonding that involves Coulomb ﬁelds of multiple nuclei, the applicability is

limited by the covalent sharing of orbital states that are not fully orthogonal.

The reader is cautioned that these diagrams are used to sort out the electron occupancies of the

orbital ground state in order to anticipate the quantum designation of the ground state. The virtue of

the one-electron models is the ready insight that they can provide without the necessity of complex

mathematical analysis and computation.

In collective-electron band theory that was introduced by Stoner [30], the Fermi level is used

as the reference energy for electrical properties, and it has been found phenomenologically con-

venient to separate the spin populations into up (majority ’) and down (minority “) spin bands

based on the difference in energy between the upper and lower parts of the d -shell spin ladders

depicted in Fig. 2.3. This model is then used to explain the net collective moment in the manner of

a ferrimagnetic spin system.

76 2 Magnetic Ions in Oxides

Fig. 2.19 Origin of the low-spin state of d

shown in (b), where the upper “ half is depicted as

a virtual shell of energy U

.(a) is extracted from Fig. 2.8 to serve as an energy reference. For

10Dq < U

, all four spins are aligned parallel, producing S D 2 in the ’ states. When the

crystal-ﬁeld splitting increases to 10Dq

, the single e

’ spin will ﬂip as it can now stabilize

in the t

states of the “ shell, both satisfying the Pauli principle and creating a low-spin value of

S D 1. Note that in the one-electron approximation, the IP energy information from (a) associated

with the U

D e

correlation energy has been discarded

the “low-spin” states that occur in strong crystal ﬁelds (in violation of Hund’s

rule when the destabilization from the 10Dq splitting energy overrides the e

spin polarization energy that we designate U

In the weak-ﬁeld limit, the spins are polarized to the maximum extent and the re-

sult is logically called the “high-spin” state. Although these spin alignments are the

usual situations in the 3d

series, low-spin occupancies may also occur in selected

instances where 10Dq>U

. When this occurs, the lower half of the 3d

shell be-

gins to ﬁll before the upper one is half-ﬁlled, as illustrated by the example of 3d

in Fig. 2.19b. In most situations, stable low-spin condensations are not expected un-

less cation valences exceed 3C in octahedral sites. The example chosen here (3d

2.4 Orbital Energy Stabilization 77

the Jahn–Teller case to be discussed in the next section, is not usually expected to

condense into a low-spin conﬁguration unless the valence increases to 4C,forex-

ample, the infrequently encountered Fe

ion. A more likely situation where U

can exceed 10Dq would be found with n D 6 in an octahedral site. Co





in a

perovskite lattice is analyzed for high, low, and intermediate spin conﬁgurations by

Ibarra et al [31]. A detailed diagram in the manner of Fig. 2.19b is included to illus-

trate the application of these concepts to a challenging problem. The magnetoelastic

implications of this family of ions are discussed further in Chap. 5 (see Fig. 5.7).

In general, low-spin states do not occur in tetrahedral sites because of the 4/9

reduction factor in the value of Dq, but the hypothetical conﬁgurations are included

here for completeness. The respective d -electron diagrams are included in Figs. 2.17

and 2.18, and the corresponding stabilization energies in units of Dq are listed in

Tables 2.12 and 2.13. Comparison of these estimates of site stabilization energy can

be used to decide the likely preference for ions in lattices such as spinels and garnets

Table 2.12 High- and low-spin d -electron stabilization energies in an octahedral coordination

d Electrons

High-spin

conﬁguration

Stabilization

energy

Low-spin

conﬁguration

Stabilization

energy





4Dq





4Dq





8Dq





8Dq





12Dq





12Dq









6Dq





16Dq













20Dq









4Dq





24Dq









8Dq









18Dq









12Dq









12Dq









6Dq









6Dq

















Table 2.13 High- and low-spin d -electron stabilization energies in a tetrahedral coordination

d Electrons

High-spin

conﬁguration

Stabilization

energy

Low-spin

conﬁguration

Stabilization

energy





6Dq





4Dq





12Dq





8Dq









8Dq





18Dq









4Dq





24Dq

















20Dq









6Dq









16Dq









12Dq









12Dq









8Dq









8Dq









4Dq









4Dq

















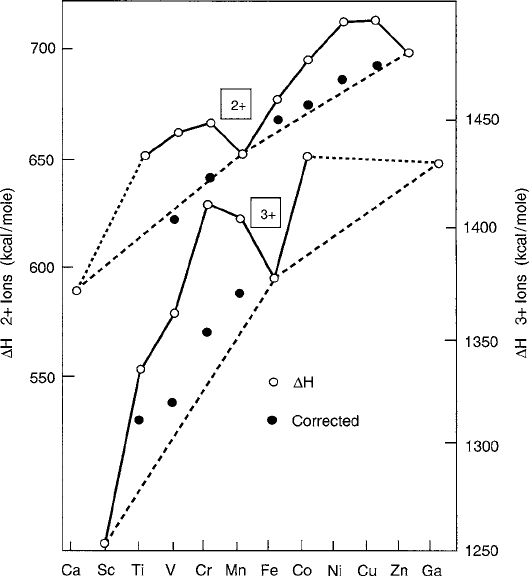
78 2 Magnetic Ions in Oxides

Fig. 2.20 Heats of hydration of divalent and trivalent transition metal ions as a function of atomic

number. Ligand ﬁeld energies are subtracted from total values to reveal the expected smooth

monotonic increase in binding energy with increasing atomic number. Data are from Holmes and

McClure [32]

where both octahedral and tetrahedral sites are present. For the speciﬁc example of

, a site preference energy of 4Dq can be deduced from the stabilization energies

listed in the tables.

The success of this simple model may be observed from the heat of hydration

data of Holmes and McClure [32] plotted Fig. 2.20, where the excess binding energy

attributed to the octahedral ligand ﬁeld stabilization is seen to follow the values

predicted in Table 2.12 for the high-spin case. Of the various 3d

ions, the most

dramatic example of a transition from high spin to low spin is 3d

,i.e.,Fe

whereby the spin value can decrease from S D 5=2 to 1/2 when Dq=B>3

in Fig. 2.21, adapted from the calculations of Tanabe and Sugano [33]. Such a low-

spin state occurs for isolated Fe

ions in K

.CN

/ as observed in electron

spin resonance (EPR) measurements [34]. With .CN

6

ligands, this intriguing

situation is examined in relation to spin–lattice relaxation in Sect. 6.2.Co

.3d

also has a low-spin conﬁguration in an octahedral site [35], where all six electrons

ﬁll the t

shell producing S D 0 instead of 2.

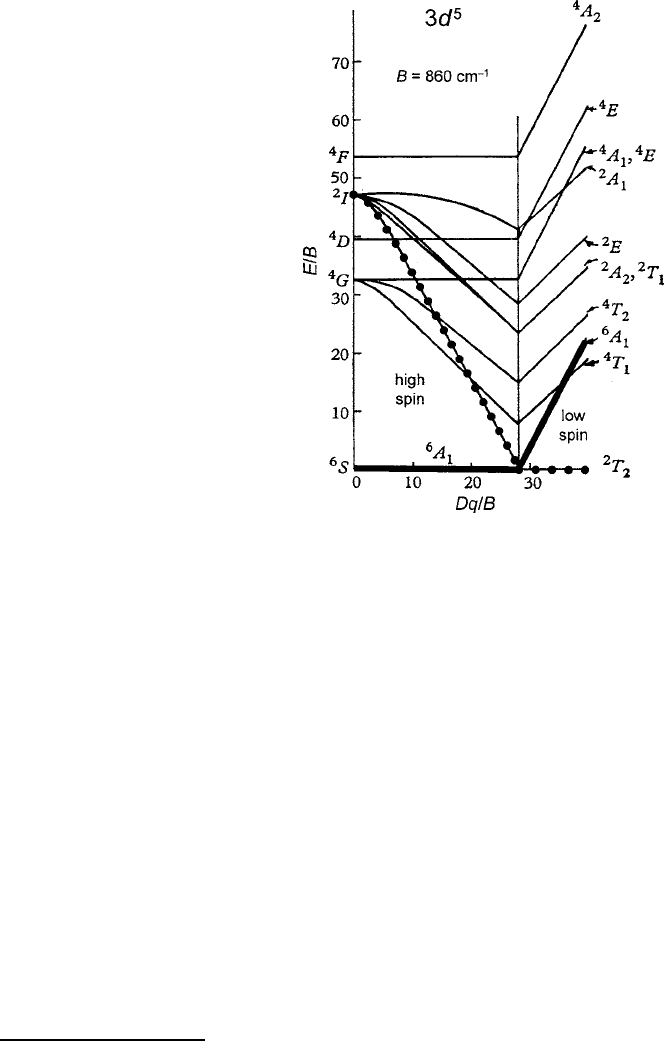
2.4 Orbital Energy Stabilization 79

Fig. 2.21 Splitting of states

of the d

conﬁguration by an

octahedral ﬁeld (abbreviated

and modiﬁed from Tanabe

and Sugano calculations

[33]). The Racah parameter



D860 cm

1



represents

the effect of the internal spin

polarization energy U

Fig. 2.19b. Note the transition

from a high-spin orbital

singlet

ground term to a

low-spin orbital triplet

when Dq=B > 3

From the tables and ﬁgures presented so far, it is evident that the cubic ﬁelds

alone fail to remove all of the ground-state degeneracy. Further stabilization can

occur, and there are two mechanisms by which this can take place locally: (1) orbit–

lattice coupling manifested in the now-celebrated Jahn–Teller (J–T) spontaneous

distortion effects, and (2) the more conventional spin–orbit (S–O) coupling that can

override and reverse the J–T distortion in select cases. Both of these phenomena are

responsible for important magnetic and electronic behavior.

2.4.3 Orbit–Lattice Stabilization (Jahn–Teller Effects)

In Figs. 2.17 and 2.18 that were discussed in relation to the single d electron

approximations in octahedral and tetrahedral sites, it is evident that in many cases

not all of the degeneracy is removed by quenching of the orbital angular momen-

tum in cubic ﬁelds. Group theory dictates that lower symmetry arrangements of

the oxygen ligands can lift the remaining degeneracies and eliminate all vestiges of

unquenched orbital angular momentum in the ground states.

Except for situations

It should be pointed out that this lifting of degeneracies does not include those of Kramers dou-

blets, which are spin degeneracies that can be split only by magnetic ﬁelds. Kramers doublets occur