Dionne G.F. Magnetic Oxides
Подождите немного. Документ загружается.

90 2 Magnetic Ions in Oxides
the molecule. In transition-metal cations, these orbital states are the eigenfunc-
tions of the particular crystal field in which the ion resides. As a result, the focus
of the molecular orbital analysis is specifically the interaction between individ-
ual electron orbitals rather than the combined result of multielectron orbital wave
functions, in the manner of the weak rather than strong crystal field approach. At-
tractions between nuclei and electrons are therefore not treated as competing with
the electron–electron repulsive perturbation, but rather grouped as part of the overall
crystal lattice energy.
For a generic heteronuclear diatomic molecule with metal ions a and b,the
individual orbital wavefunctions are hybridized into linear combinations (LCAO)
from the corresponding one-electron (nonorthogonal) orbital functions '
a
and '
b
according to
'
D N
.
'
a
'
b
/.antibonding state/ (2.35a)
and '
C
D N
C
.'
a
C
C
'
b
/.bonding state/; (2.35b)
where N
C
D
1 C
2
C
C
C
ab
1=2
and N
D
1 C
2
–
ab
1=2
are the nor-
malization coefficients, if desired, and
ab
D
h
a
j
b
i
is the density of the orbital
wavefunction overlap or simply the overlap integral. It represents a probability
that can vary from 0 to 1. Thus, the covalent sharing of orbital states by local-
ized electrons within the overall ionic bonding scheme is represented by the terms
C;
ab
1. (If the molecule is homonuclear, such as H
2
,
C;
D 1). The spatial
probability densities '
2
C
and '
2
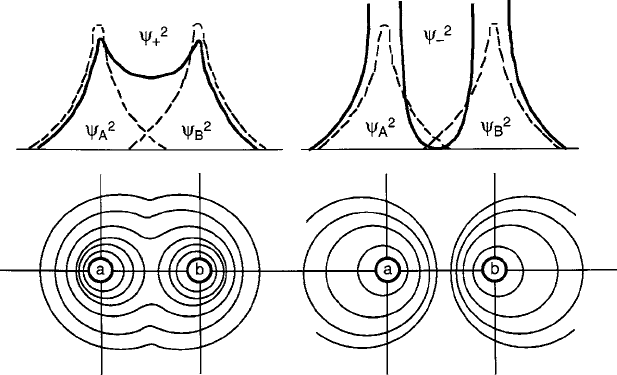
are depicted by the sketches in Fig. 2.30.Where
the electrons can be delocalized in the overlap volume between the nuclei, spins are
Fig. 2.30 Schematic of bonding and antibonding states for spherically symmetric s-electron wave-
functions of two similar atoms A and B, showing the probability distributions of electron charge
between them. Except in ferromagnetic cases with partially filled d shells, the more stable is called
the bonding state with greater charge density between the nuclei

2.5 Covalent Stabilization 91
aligned antiparallel in observance of the Pauli principle, and the energy is reduced
because the electrons screen the repulsive forces between the two positively charged
nuclei. For this reason, '
C
is called the “bonding” state; the opposite condition oc-
curs in the “antibonding” state '
because wavefunction charge clouds repel each
other, thereby restoring orthogonality.
8
In this case, spin directions can return to the
more natural parallel alignment in observance of Hund’s rule of maximum spin po-
larization. Note also that the unnormalized density function of the bonding state
j'
C
j
2
is greater than that of the antibonding state j'
j
2
, consistent with a net stabi-
lization energy gained by the wavefunction overlap (see Appendix 2A). From this
elementary approximation it can be concluded that antiparallel spin alignment re-
quires the nonorthogonality of '
a
and '
b
.
2.5.2 Determinant Method
Estimates of the molecular orbital eigenfunctions can be obtained by solving
two-level perturbation problems in the standard way, guided by the abbreviated
Hamiltonian for the interaction of two empty orbital states
H D H
a
C H
b
D
„
2
=2m
e
r
2
a
C
Z
a
e
2
r
a
CV
a
„
2
=2m
e
r
2
b
C
Z
b
e
2
r
b
CV
b
;
(2.36)
where the V
a
and V
b
represent latent contributions from the respective cross-nuclear
terms Z
a
e
2
=r
b
and Z
b
e
2
=r
a
, here treated as constant along the bond axis. The
interionic energies are treated in this manner because a one-electron solution, for
example, for H
C
2
, is sought as a molecular-orbital base analogous to the 3d
1
crystal
field model. These interactions are also diminished by screening from the electron
(1)–electron (2) repulsive energy (normally stated as e
2
=r
12
) that is taken into ac-
count by a semiempirical factor that modifies the off-diagonal matrix term defined
later. For the example of overlapping orbital functions of ions with effective nuclear
(valence) charge Z
a
and Z
b
and respective ionic radius r
a
and r
b
, the stabiliza-
tion energy and coefficients of hybridization can be approximated from a matrix
perturbation method applied to a diatomic molecule, as described in Ballhausen
[44], with a detailed derivation in Ballhausen and Gray [45]. In this method, a self-
consistent term appears in the secular equation
ˇ
ˇ
H
ij
E.ı
ij
1 ı
ij
ij
ˇ
ˇ
D 0 for
the determinant
ˇ
ˇ
ˇ
ˇ
H
aa
E H
ab
E
ab
H
ba
E
ba
H
bb
E
ˇ
ˇ
ˇ
ˇ
D
ˇ
ˇ
ˇ
ˇ
E
a
Eb
ab
E
ab
b
ba
E
ba
E
b
E
ˇ
ˇ
ˇ
ˇ
D 0; (2.37)
8
'
C
is called the “bonding” state and is often designated by a subscript g (for gerade or even).
The opposite effect occurs with the “antibonding” state '
, which would be indicated by a u (for
ungerade or odd) subscript.

92 2 Magnetic Ions in Oxides
where
H
aa
D
h
'
a
j
H
j
'
a
i
D E
a
h
'
a
j
'
a
i
D E
a
;
H
bb
D
h
'
b
j
H
j
'
b
i
D E
b
h
'
a
j
'
a
i
D E
b
; (2.38)
H
ab
D H
ba
D b
ab
h
'
a
j
h
ab
.E
a
C E
b
/
j
'
b
i
D h
ab
.E
a
C E
b
/
h
'
a
j
'
b
i
h
ab
.E
a
C E
b
/
ab
:
where b
ab
is the electron exchange or transfer integral between states of energy E
a
and E
b
,
9
ab
D
h
'
a
j
'
b
i
1 is the orbital overlap integral, and h
ab
is an interionic
screening factor that typically has a value of unity for ionic bonds. This relation for
H
ab
was recommended by Wolfsberg and Helmholtz [44, 46].
To implement the solution of this equation when applied to the molecular orbital
problem, it must first be recognized that '
a
and '
b
are not part of an orthonormal set.
The respective energies E
a
and E
b
of the '
a
and '
b
states appear on the diagonal of
the determinant in (2.37) and correspond to those of the outermost electrons under
the influence of the charges from their respective nuclear skeletons and valence
electrons. In an ionic molecule, the electron energy E
a
of the cation at site a can be
estimated from the ionization potential of the cation outer electron destabilized by
the repulsive field of the negative anion (the source of the anisotropic crystal-field
perturbation), and E
b
from the electron affinity of the anion outer electron stabilized
by the attractive field of the positive cation.
10
To be Hermitian, however, H
ab
must
equal H
ba
. Because these determinant elements represent the transfer or exchange
integral b
ab
of the tight-binding approximation, it is reasonable to adopt a singular
value of b
ab
D b.
This expression for H
ab
in (2.38) is based on the assumption that E
a
and E
b
are nearly uniform within the overlap region as suggested by Fig. 2.30.Thevalues
of E
a
and E
b
are defined graphically in the simple molecular orbital diagram of
Fig. 2.31 as the stabilization energies of the outer electrons on the respective ions.
Note that the values of E
a
and E
b
are negative, with E
a
chosen to be of lower en-
ergy. Regardless of what the exact expression for H
ab
is, the earlier exercise points
out that the magnitude of the transfer integral b is jointly dependent on the atomic
stabilization energy of the electrons involved in covalent bond and the volume
fraction of overlap .
General solutions of (2.37) for the bonding .C/ and antibonding ./ states are
as follows:
9
In this model, all electronic energies are referenced to the zero energy of the free ion. E
a
or E
b
is
the algebraic sum of its ionic stabilization energy (the cation ionization potential or anion electron
affinity) and the electrostatic potential from the charge on its neighboring ion.
10
When applied to ionic bonds, the covalent electrons are treated as initially localized on their
nuclei, as in the case of the O
2
anion with its filled 2p shell. As a result, the Hund’s rule re-
pulsion arising from a dominant e
2
=r
ij
internal exchange term is absent, which then precludes the
possibility of itinerant ferromagnetism from an antibonding band.

2.5 Covalent Stabilization 93
Fig. 2.31 Basic two-ion molecular orbital diagram, with one electron per ion. According to the
Aufbau method, both would be expected to favor the lower energy bonding state '
C
E
˙
D
E
a
C E
b
2b ˙
q
.E
a
C E
b
2b/
2
4.E
a
E
b
b
2
/.1
2
/
2.1
2
/
:
(2.39)
If we now substitute b D h.E
a
C E
b
/,(2.39) will be expressed as
E
˙
D
E
F
1 2h
2
˙
1
2
q
U
2
.1
2
/ C b
2
.2h 1/
2
=h
2
1
2
; (2.40)
where E
F
D.E
a
C E
b
/=2 is the unscreened average electron energy, and the un-
screened excitation energy U DE
a
–E
b
, so chosen to set its value negative and there-
fore consistent with the other energy parameters. The influence of h is illustrated in
Appendix 2A for a homonuclear molecule, for example, H
2
,forwhichE
F
D E
a
D
E
b
.Ifh<0, the antibonding state can be stabilized, thereby implying the implicit
screening effect of the e
2
=r
12
repulsive energy. Based on the findings of Wolfsberg
and Helmholz [46], the parameter h 1 for ionic compounds, which selects the
positive solution to be the ground orbital state. An antiferromagnetic spin pairing
with the symmetrical hybridization is required for Pauli antiparallel spin ordering of
a bonding state. For oxides, (2.40) simplifies to
E
˙
D
E
F
1 2h
2
˙
1
2
p
U
2
.1
2
/ C b
2
1
2
: (2.41)
A further approximation can be made for
2
<< 1,
E
˙
D E
F
˙
1
2
p
U
2
C b
2
: (2.42)
There is a procedure to determine the value of by computation [46], but in practice
<1can be treated as a semiempirical parameter to be deduced from experiment
[47,48].
Eigenfunctions of the E
C
and E
levels can now be determined by forming the
hybrid linear combinations

94 2 Magnetic Ions in Oxides
'
D N
.c
ba
'
a
c
bb
'
b
/.antibonding/
'
C
D N
C
.c
aa
'
a
C c
ab
'
b
/.bonding/; (2.43)
and N
D
c
2
ba
C c
2
bb
2c
ba
c
bb
1=2
and N
C
D
c
2
aa
C c
2
ab
C 2c
aa
c
ab
1=2
.Ex-
pressed in terms of the corresponding LCAO coefficients, c
ab
Dc
ba
D
C;
.Thec
ij
coefficients are then determined from the relation
P
ij
fH
ij
EŒı
ij
1ı
ij
ij
gc
ij
D0
for each solution value of E. Accordingly, we can write
.b E
/c
ba
C .E
b
E
/c
bb
D 0;
.E
a
E
C
/c
aa
C .b E
C
/c
ab
D 0: (2.44)
After recognizing the normalizing conditions N
2
c
ba
2
C c
bb
2
D 1 and
N
C
2
c
2
aa
C c
2
ab
D 1, we obtain the general relations
N
2
c
ba
2
D
"
.E
b
E
/
2
.E
b
E
/
2
C .b E
/
2
#
;
N
2
c
bb
2
D
"
.b E
/
2
.E
b
E
/
2
C .b E
/
2
#
;
N
C
2
c
aa
2
D
"
.b E
C
/
2
.E
a
E
C
/
2
C .b E
C
/
2
#
; (2.45)
N
C
2
c
ab
2
D
"
.E
a
E
C
/
2
.E
a
E
C
/
2
C .b E
C
/
2
#
:
The eigenvalues and hybrid eigenfunctions for the two extreme approximations can
now be determined for use in (2.43), recalling the definitions of b, E
F
,andU.
For strongly covalent molecules with b
2
=U
2
>> 1,(2.42) becomes mainly a
first-order perturbation, with a small off-diagonal correction
E
˙
E
F
˙
1
2
p
U
2
C b
2
E
F
˙ b=2 ˙ U
2
=4b: (2.46)
In this limit, U
2
=4b is the additional stabilization of the bonding state and can
therefore represent the trap barrier for an electron transfer between '
a
and '
b
.Itis
the bonding state energy that must be gained to escape the trap. As a consequence,
U
2
=4b is also an effective activation energy for polaronic charge transport to be
discussed in Chap. 8.
For metal-oxide compounds, the bonds are primarily ionic, with covalent electron
sharing (delocalization) more of a perturbation, giving a ratio b
2
=U
2
<< 1.Inthis
extreme, the covalent interaction is a second-order perturbation,
E
˙
E
F
˙
1
2
U
1 C b
2
=2U
2
D E
F
˙
1
2
U ˙ b
2
=4U; (2.47)
2.5 Covalent Stabilization 95
where
E
E
b
b
2
=4U antibonding;
E
C
E
a
C b
2
=4U bonding; (2.48)
E
C
E
U C b
2
=2U:
Because the transfer integral b has also been designated as a negative quantity con-
sistent with E
a
and E
b
,theb
2
=4U term represents the amount by which the hybrid
energy is stabilized by the transfer energy. For the oxide case, (2.45) simplifies to
N
2
c
ba
2
D
E
F
E
a
b
2U
2
"
1 C
E
F
E
a
b
2U
2
#
1
E
F
E
a
b
2U
2
;
N
2
c
bb
2
D
"
1 C
E
F
E
a
b
2U
2
#
1
1;
N
C
2
c
aa
2
D
"
1 C
E
F
E
b
b
2U
2
#
1
1; (2.49)
N
C
2
c
ab
2
D
E
F
E
b
b
2U
2
"
1 C
E
F
E
b
b
2U
2
#
1
E
F
E
b
b
2U
2
:
for direct application to (2.43), which can then be approximated by
'
E
F
E
a
b
2U
'
a
'
b
b
2U
'
a
'
b
; (2.50)
'
C
'
a
C
E
F
E
b
b
2U
'
b
'
a
C
b
2U
'
b
:
Note the difference between the N
C
c
ab
and N
c
ba
coefficients of (2.49), which is
similar to (2.45). This arises from the nonzero overlap integral . ¤ 0/, as described
in Appendix 2A together with the implications of normalization. For preliminary
estimates, E
F
=E
b
and E
F
=sE
a
can be set to unity. The square of coefficient b=2U
then represents the lesser fractional shares of the starting '
a
and '
b
functions in their
respective '
C
and '
hybrid eigenfunctions.
2.5.3 and Bonds and the Molecular Orbital Diagram
A thorough discussion of the symmetry contributions to covalent bonding will not
be attempted in this text, but an appreciation of its importance can be introduced
through the definition of the primary types of overlap interactions. For the transition-
metal oxides, we need only to consider the influence of an unfilled d electron shell
96 2 Magnetic Ions in Oxides
and its interaction with the 2p shell of the O
2
ligands. Although the electrons in
the outer p and s shells of the cation are principally responsible for the chemical
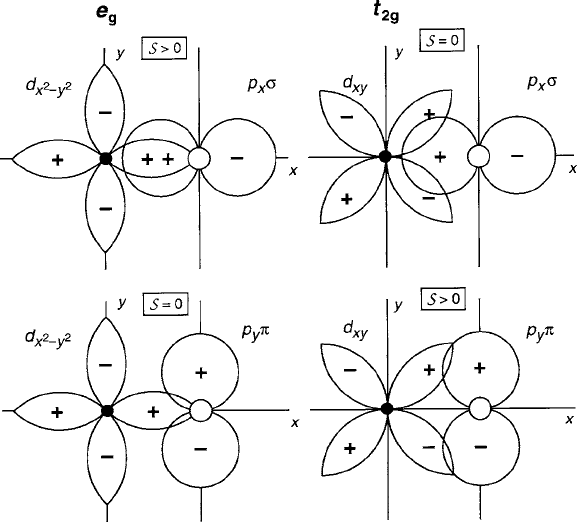
bond, the magnetic properties enter through the d shell. In Fig. 2.32, four examples
are sketched for the d –p orbital lobe arrangements characteristic of transition-metal
ions in octahedral oxygen coordinations.
The two principal factors that determine the magnitude of are as follows: (1)
the amount of spatial overlap of the cation d and ligand p orbital lobes, designated
according to whether the ligand lobe is directed along the axis joining the two nu-
clei (¢ bonds) or at a significant angle to it ( bonds), and (2) the relative signs of
the lobes. A rule often followed is that a nonzero overlap integral will occur if
both orbitals have the same symmetry about the axis joining the two nuclei.From
inspection of the examples in Fig. 2.32 we observe that e
g
d
x
2
y
2
–p
xy
¢ provides
the largest and strongest bond while t
2g
d
xy
– p
x;y
can also contribute, but
through a significantly weaker interaction. Similar constructions can also be made
for the e
g
d
z
2
–p
xy
¢, couplings. The possible influence from e
g
–p and t
2g
–p
is deemed negligible because the orthogonality of the lobe polarities would produce
cancellation. For a first-order estimate of covalent energy in octahedral complexes,
only e
g
–p¢ is generally taken into account in determining the bonding and anti-
Fig. 2.32 Illustrations of the difference between ¢ (direct overlap with oxygen 2p orbital lobes di-
rected at the cation nucleus) and (oblique overlap with oxygen p orbital lobes directed orthogonal
to the cation nucleus). Example is given for the x y plane
2.5 Covalent Stabilization 97
bonding states, while the t
2g
orbitals in octahedral sites are treated as inactive or
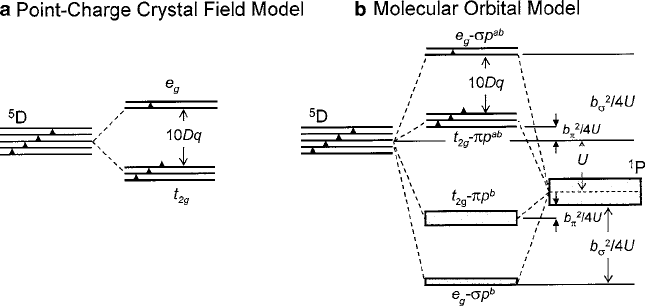
“nonbonding.” In Fig. 2.33, schematic energy level diagrams illustrate the relation
between the point-charge crystal-field approximation described in Sects. 2.3 and 2.4
and the molecular orbital model for a generic 3d –2p octahedral-site compound,
typically a transition-metal oxide, for example, Mn
3C
–O
6
. In this case, the anion is
shown with the lower energy. The bonding (b) and antibonding (ab) hybrid states for
the separate e
g
and t
2g
shells are sketched in conformance with Fig. 2.31. To empha-
size the Aufbau occupancy expectation, the bonding states are presented as occupied
mainly by the 2p paired spins from the fully populated anion states. The 3d spins
from Mn
3C
3d
4
would then occupy the e
g
–2p¢ antibonding states, beginning
with the t
2g
–2p nonbonding levels separated by b
2
¢
=4U from the e
g
–2p¢ an-
tibonding levels, which can be shown to be consistent with measured values of
10Dq2 eV. To extend these concepts further, note that large Dq stabilizes low-
spin (spin-paired) configurations. In cases of two ions with unpaired spins, large
b
2
=4U will tend to stabilize an antiferromagnetic ground state. In addition, large U
means high ionicity and large b strong covalence.
In tetrahedral sites, the bond angle between cation and anion differs substantially
from those of octahedral sites, and the t
2g
orbitals become stronger contributors
because the ligands reside along the cube body diagonals, as evident in Fig. 2.5.Itis
also for this reason that the actual value of Dq is negative, which is accounted for by
showing with the doublet stabilized relative to the triplet, as illustrated in the one-
electron models of Figs. 2.17 and 2.18. In later sections dealing with ferrimagnetic
oxides, bond angles will be seen to play an important part in the magnetic exchange
properties.
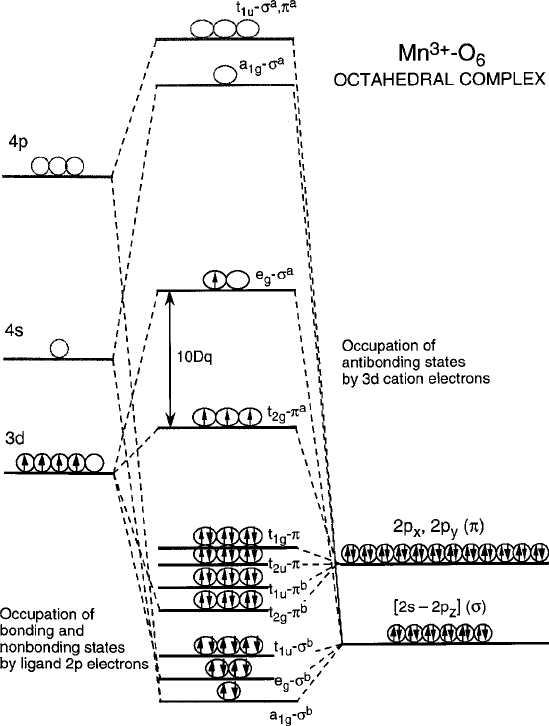
In Fig. 2.34 a complete molecular orbital energy level diagram including 4s and
4p states is shown for a 3d
4
transition metal ion and oxygen ligands in an octahedral
coordination. To a first approximation, the diagram could be constructed by com-
puting bonding and antibonding states for each of the metal levels linked covalently
to the oxygen 2p states in the manner of Fig. 2.33. Once this diagram is formed, the
Fig. 2.33 One electron point-charge crystal-field energy-level structure contrasted with molecular-
orbital model for a d
4
configuration
98 2 Magnetic Ions in Oxides
Fig. 2.34 Basic molecular orbital energy diagram for an
Mn
3C
–O
6
complex. Note that the
Mn
3C
four d electrons occupy mainly the nonbonding
t
2g
–p
ab
and antibonding
e
g
–¢p
ab
states
individual molecular orbital states are then assigned electrons from the two partic-
ipating ions according to Hund’s rule and the Aufbau principle that was employed
previously in the one-electron ground state models of the crystal-field theory. As
indicated, the low-energy bonding states are mainly 2p states that fill with spin-
paired electrons from the oxygen ligands in the fractional amount N
C
2
c
aa
2
for each
hybrid orbital combination, while the antibonding distributions would favor the ¢-
bonding e
g
states in the corresponding fraction N
2
c
bb
2
. Note also that the weaker
-bonding t
2g
electrons are designated as nonbonding and are considered to remain
in their initial cation orbital states. To place the crystal-field orbital angular mo-
mentum quenching in the context of the full molecular orbital scheme, the 3d and
2p spin occupancies of an Mn
3C
d
4
ion in an oxygen octahedral complex are
2.5 Covalent Stabilization 99
included in Fig. 2.33b. Note how the 10Dq splitting between the t
2g
and e
g
states is
retained, although relabeled as antibonding t
2g
–
a
and e
g
–¢
a
to conform to the ex-
panded nomenclature. Because of the weak t
2g
–p
a
bonding, the e
g
–p¢
a
–t
2g
–p
a
energy splitting 10Dq can be roughly equated to antibonding destabilization energy
b
2
=4U from (2.48).
Although situations in which the earlier two-level model can be applied with
some degree of rigor are relatively uncommon, the approximation can be very
helpful in providing insight on a qualitative basis. In later chapters, such applications
will be demonstrated in problems that involve magnetic exchange, magnetoelastic-
ity, magneto-optical effects, polarized spin transport, and superconductivity.
2.5.4 Valence Bond Method
Although the one-electron molecular orbital method is sufficient for most of the dis-
cussion of spin ordering and polarized spin transport on a qualitative level, the
valence bond concept is used as the basis for quantitative analyses that involve
multielectron interactions [43]. This is analogous to the difference between the
one-electron crystal field approximation and the multielectron solutions required
for interpretation of paramagnetic resonance spectra. The valence bond method was
introduced by Heitler and London [7] in their analysis of the H
2
molecule and later
generalized by Pauling [49] for application to a wide variety of molecular struc-
tures comprising dissimilar atoms. For bonding energy calculations, each atom is
assigned a valence state after a specific lattice structure is defined. Depending on
the location of the atomic components in the Periodic table, the lattice bonding is
described in terms of varying degrees of ionic and covalent.
In a diatomic molecule made up of radically different elements such as an alkali
halide, the bond is almost entirely ionic. The basic interaction of ionic bonding is
the Coulomb attraction between positive and negative charges of the cations .C/
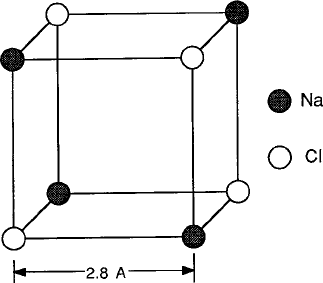
and anions ./. The simplest example is sodium chloride NaCl with Na
C
and Cl
ions occupying alternating sites at the corners of a cubic unit cell shown in Fig. 2.35,
Fig. 2.35 Basic unit cell of
an Na
C
Cl
ionic lattice
