Dionne G.F. Magnetic Oxides

Подождите немного. Документ загружается.

80 2 Magnetic Ions in Oxides

where the lattice itself furnishes the lower symmetry through its own point group,

the sources for such lower symmetry ﬁeld components are not always apparent.

In other cases there may be crystal ﬁeld components of lower symmetry that exist

locally because of lattice vacancies or variations in neighboring cation charges situ-

ated along the relevant crystal axes. In two particular situations of great importance

in determining many magnetic and magnetoelastic properties, the distortion may

occur spontaneously at the cation site because of orbit–lattice or spin–orbit–lattice

interactions peculiar to the electron conﬁguration of the transition ion.

In studies of the paramagnetic resonance behavior of Cu





ions in hy-

drated salts [36], Jahn and Teller [37, 38] noted the presence of a tetragonal

component to the crystal ﬁeld in a normally cubic octahedral site. Their explana-

tion for the phenomenon was as elegant as it was important. In situations where

a molecule has a degenerate orbital angular momentum state, the immediate envi-

ronment of the site will be found to have lower symmetry if such a distortion will

lift the degeneracy to provide a state of lower energy for the electrons that occupy

the degenerate state, that is, an increased site stabilization energy. In its elemen-

tary deﬁnition, the Jahn–Teller (J–T) effect produces a singlet orbital ground state,

which may still retain is spin degeneracy, for example, a Kramers doublet. Such

Jahn–Teller distortions can be locally static and can spontaneously deform the lattice

from cubic to tetragonal (or lower) through cooperative involvements of many sites

if the density of local distortions is high enough. If the J–T interaction is weaker,

it can manifest a dynamic behavior in which vibronic normal modes of the ligand

complex are active. This topic is discussed in detail in references already cited, and

this text will not dwell on esoteric material that might serve only to distract the

reader. There are, however, some important points that should be made clear about

variations of the distortion effects that can take place for speciﬁc members of the

transition ion series. Their inﬂuence on magnetoelastic effects and resonance relax-

ation processes is reviewed in Chaps. 5 and 6.

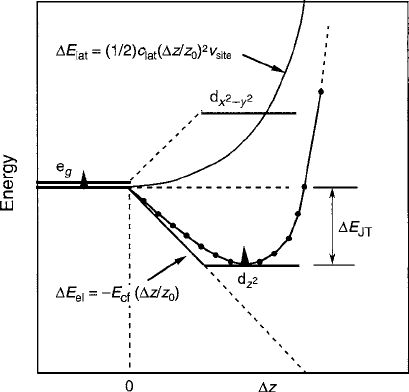
The Jahn–Teller effect in its essential form may be seen from the simple

schematic picture of Fig. 2.22. The example shows a single electron in the e

orbital doublet of an octahedral crystal ﬁeld of energy E

. A tetragonal crystal

ﬁeld component from a <100> z-axis distortion splits the doublet to create an

electronic stabilization energy E

that is equal to the product of E

and the z-axis

strain, that is, E

D E

.z=z

/,wherez

is the initial length of the octahedron.

To establish equilibrium in the localized system, E

is offset by an increase in

lattice elastic energy E

lat

for the site of volume v

site

, which is approximated as

quadratic in the form of E

lat

D .1=2/ c

lat

.z=z

site

. The reduction in energy

of the electron that occupies the lower half of the split doublet is determined by

with a noninteger spin quantum number, that is, S D 1=2, 3/2, 5/2, etc., resulting from ions with

odd numbers of unpaired electron spins. Care must be exercised in the use of the exchange ﬁeld

concept. It is not a true magnetic ﬁeld in the Maxwell sense. It is born out of covalent bonding

and the Pauli exclusion principle of indistinguishability and is therefore of electrostatic origin. It

can be only a scalar and has neither the ability to polarize the spins that it gathers along a chosen

direction nor to split Kramers doublets.

2.4 Orbital Energy Stabilization 81

Fig. 2.22 Generic model of

the Jahn–Teller effect

minimizing the net J–T stabilization deﬁned as E

D E

lat

–E

, plotted as a

function of the strain z=z

. From this simple analysis, the equilibrium value of

z=z

D E

lat

site

, and the static Jahn–Teller stabilization energy becomes

E

D .1=2/ E

lat

site

: (2.32)

For a typical oxide compound E

 10Dq  2 eV, the lattice elastic constant

lat

 2 10

dyne cm

, and the site volume v

site

 10

23

. These values then

predict a J–T strain  0:15 and a E

 0:2 eV or 1; 500 cm

1

The double-valued solution for z conﬁrms that either expansion or contrac-

tion can occur along the z axis, causing the energies of the d

y

and d

levels

to reverse accordingly. For this reason, the J–T effect can be temperature depen-

dent, diminished thermally by the growth of the random lattice phonon population,

and speciﬁcally by the vibronic modes of the local cation–anion conﬁguration [39].

When the latter conditions dominate, the stabilization of the electronic ground

state is compromised by the blurring of the e

orbital levels if the occupying elec-

trons cannot keep up with the vibronic ﬂuctuations, and doublet degeneracy can be

restored. Otherwise, the electronic stabilization is preserved and the resulting con-

dition is termed “quasistatic” in a manner that is difﬁcult to distinguish from the

simple static effect prevalent at low temperatures [40]. What distinguishes the pure

J–T effect from other spontaneous lattice distortions is that the d

y

and d

states

involved in the splitting each have zero orbital angular momentum, that is, m

D 0.

For J–T splitting of the e

doublet, there are four situations among the high-spin d

electron transition groups where this can occur in an octahedral site. As diagrammed

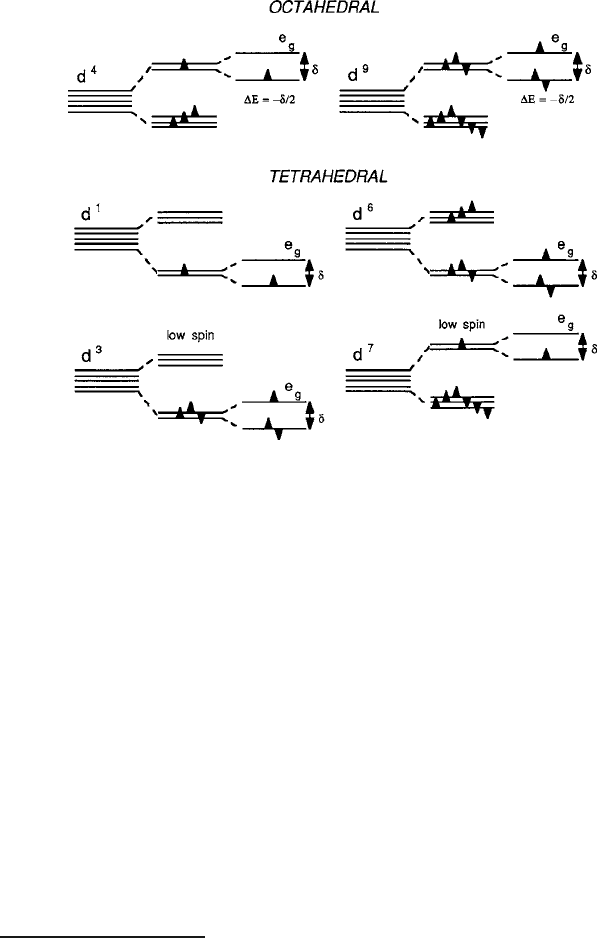
82 2 Magnetic Ions in Oxides

Fig. 2.23 One-electron model of Jahn–Teller stabilizations of the e

states

in Fig. 2.23,theyared

and d

in octahedral and d

and d

in tetrahedral sites.

the low-spin conﬁgurations are considered, d

and d

ions in tetrahedral sites are

also subject to Jahn–Teller e

splittings. The different J–T effects reveal themselves

in various situations that involve magnetoelastic properties as well as electrical con-

ductivity related to polaron activity that is discussed in Chap. 8.

2.4.4 Spin–Orbit–Lattice Stabilization

In the context of local magnetoelastic effects, it is appropriate here to point out an

important implication of the spin–orbit coupling perturbation energy. In reviewing

the crystal ﬁeld orbital occupancy diagrams for the ground state in Figs. 2.17 and

2.18, one observes that certain t

conﬁgurations remain degenerate because of par-

tially ﬁlled states. Unlike the e

doublet with m

D 0 that undergoes a pure J–T

A point worthy of note concerns the infrequent situation of d

in a tetrahedral

site. Such

a case is Fe

substituting for Zn

in a ZnO lattice. According to Fig. 2.23, a pure Jahn–Teller

effect is expected in the e

orbital ground states. The energy of this stabilization, however, would

be signiﬁcantly less than that of Mn

or Fe

in an O

site because of the 4/9 reduction in the

crystal-ﬁeld strength combined with the lower valence charge of the Fe

cation. This occurrence

of the J–T effect is analyzed by Goodenough [41].

2.4 Orbital Energy Stabilization 83

splitting independent to ﬁrst order of spin–orbit interactions, the t

triplet con-

tains both a singlet d

with m

D 0 and doublet d

xz;yz

orbitals with nonzero

D˙1 because they are hybrids of t

/ and t

1

/ from (2.11), as ex-

plained in Sect. 2.3.3. Therefore, by deﬁnition, the t

states also can be split by a

J–T effect if the d

singlet emerges as the ground state. However, if the spin–orbit

coupling LS exceeds the J–T ı splitting, an orbitally degenerate ground state can

also occur if the hybridized d

xz;yz

orbitals are stabilized. Furthermore, unlike the e

splitting that requires a tetragonal or orthorhombic distortion along a <100> axis,

the t

J–T splitting can occur by either <100> or trigonal axis <111> distortions,

as indicated by Fig. 2.13. This latter condition has implications for the design of

anisotropy and magnetostriction in ferrites.

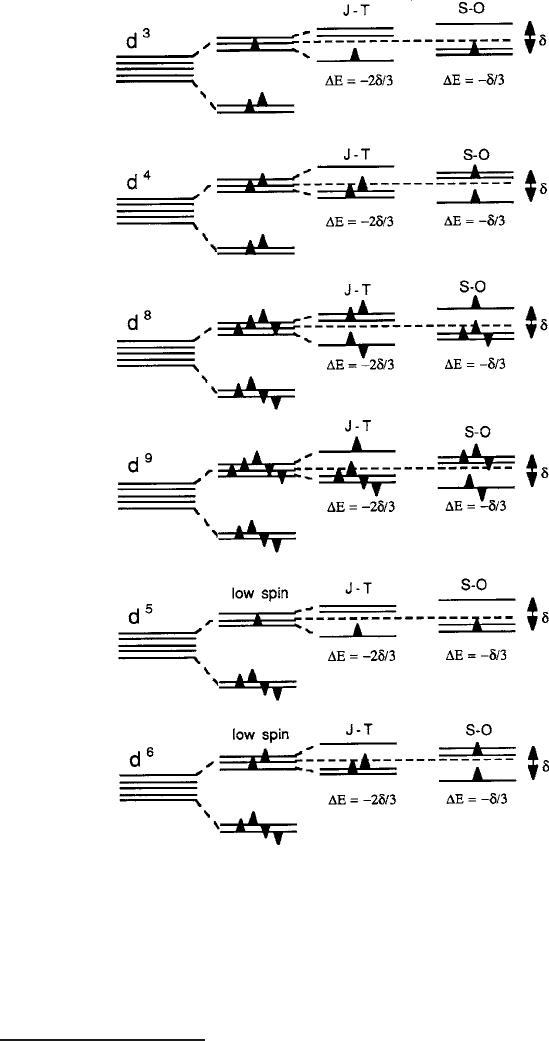
Sketches of the doublet orbital lobes are shown in Fig. 2.24. The preference for

one sign of distortion over the other lies in the relative magnitudes of ı and the

spin–orbit coupling energy . Where an exchange ﬁeld H

imposes ordering of

the spins along the axis of the unquenched orbital angular momentum, spin–orbit

coupling can stabilize the doublet as an alternative ground state that is manifested as

a collective distortion of the opposite sign, as depicted in the tutorial sketch of the

perturbed orbital states in Fig. 2.25. This possibility is represented throughout the

various t

spin occupancy situations shown in Figs. 2.26 and 2.27. The sign of

the lattice deformations can be a guide to which effect is occurring in a particular

situation.

The basic requirement for S–O stabilization is the retention of a nonzero L in

the ground state, which would mean a degenerate state in the ideal case. As indi-

cated in Fig. 2.28 for the example of a single d electron in an octahedral site, both

an axial crystal ﬁeld that produces a ı<0and a spin–orbit splitting, each acting

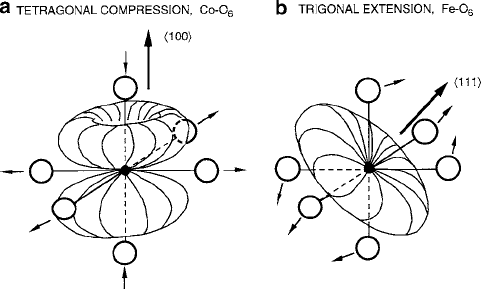
Fig. 2.24 Octahedral-site deformations from stabilization of spin–orbit doublet create ground

states in the partially quenched t

shell: (a) a single electron in degenerate hybrid d

˙ id

causes a h100i tetragonal compression (characteristic of CoO), and (b) a single electron in de-

generate hybrid of a trigonal ﬁeld produces a h111i extension (characteristic of FeO) (Based on

Figs. 44 and 53 of [40])

84 2 Magnetic Ions in Oxides

Fig. 2.25 Spin–orbit and Jahn–Teller stabilizations of the t

states

independently, can stabilize parts of the same doublet hybrid .1=



˙ id



while ı>0will produce the opposite effect. (The signs of ı reverse for a single d

“hole” in the t

shell because of the inverted level structure). In the presence of a

signiﬁcant H

, the threshold condition for S–O dominance based on this rudimen-

tary analysis is [40]:

.L  S C ı=3/  E

D 2ı=3: (2.33)

For a single d electron, S

D 1=2, and since L

D m

D˙1,(2.33) reduces to

=2 Cı=3  2ı=3

or (2.34)

=ı  2=3:

This subject is examined in greater detail for the speciﬁc 3d

ions in relation to the

magnetoelastic properties in Chap.5, supported by a quantum perturbation analysis

of the T

term under the inﬂuence of the parameters ı, ,andH

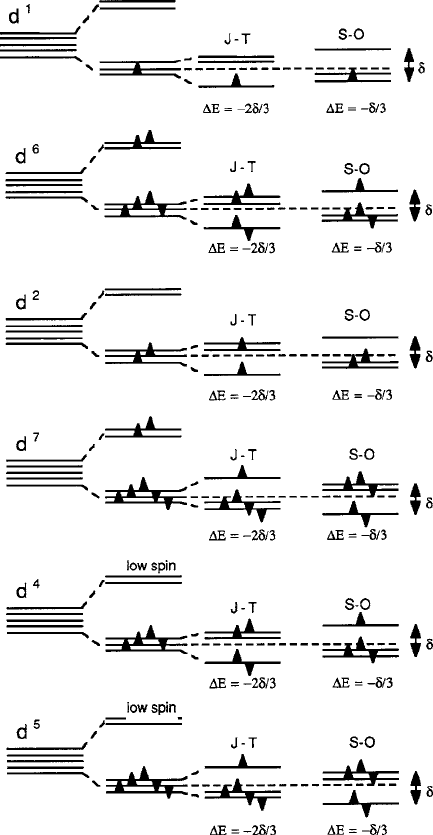
In Fig. 2.29, two common examples of the J–T and S–O stabilizations (d

and

in octahedral sites) are compared in relation to observed ligand displacements.

Note that the z-axis of a compressive distortion of the S–O case has the sign needed

to create a degenerate ground state stabilized with the m

D˙1 orbital angular

momenta. There are many instances where potential spin–orbit–lattice stabilizations

could take place. A summary of these possibilities is given in Table 2.14 with known

occurrences highlighted.

The distinction between these two spontaneous stabilization effects should be

restated because it can have important inﬂuence on the properties of magnetic ox-

ides. Because the J–T effect overrides spin–orbit coupling and stabilizes the m

D 0

singlet, cooperative manifestations of it might appear less dependent on a spin or-

dering condition (Curie or N´eel). However, the S–O effect requires collinearity of

2.4 Orbital Energy Stabilization 85

Fig. 2.26 One-electron model of J–T/S–O stabilizations of the t

shell: octahedral site

spins for cooperative distortions to occur [40] and is therefore expected only in sys-

tems where the energy gain from H

through œLS is large enough to offset the

J–T singlet stabilization. The attendant local distortions of either sign can produce

spin–lattice magnetostriction effects in spin-ordered systems, one depending on a

dominant orbit–lattice interaction with less spin–orbit coupling, and the other de-

pending on a strong spin–orbit coupling with a smaller orbit–lattice (crystal-ﬁeld)

86 2 Magnetic Ions in Oxides

Fig. 2.27 One-electron model of J–T/S–O stabilizations of the t

shell: tetrahedral site

stabilization (see Fig.2.9). If the concentration of J–T or S–O stabilized ions is high

enough, a crystallographic phase transition can take place when the temperature

decreases below a condensation threshold.

For a comprehensive discussion of this effect with Mn

and Co

in octahedral sites, the reader

is directed to Chap. III, Sect. 1E2 of Goodenough [40].

2.4 Orbital Energy Stabilization 87

Fig. 2.28 c-Axis octahedral site stabilizations of a single d spin in the context of Fig.2.25

Fig. 2.29 Examples of J–T (d

,Mn

)andS–O(d

,Co

) stabilizations

In addition to the lattice distortions, spin–orbit stabilization also brings strong

spin–lattice effects that manifest themselves in magnetoelastic properties of ferrites,

particularly with Co





ions’ octahedral sites. It should also be remarked that

any lower symmetry crystal ﬁeld, regardless of origin, that leaves an unquenched

orbital ground state can have great inﬂuence on spin–lattice relaxation properties.

These subjects are revisited in relation to the magnetoelastic and microwave behav-

iorofspeciﬁcmembersofthe3d

ion series in Chaps. 5 and 6.

88 2 Magnetic Ions in Oxides

Table 2.14 Jahn–Teller and spin–orbit Stabilized d

Ions

Pure J–T effect S–O (or J–T) effect

shell t

shell

Octahedral Tetrahedral Octahedral Tetrahedral

– d

–

––d

–

– d

(low spin) – d

– d

(low spin) d

––d

(low spin) d

(Low spin)

– d

(Low spin)

(Low spin) – d

–

(Low spin) – – d

, d

(Low spin)

–– d

These phenomena can be even more intriguing with ions of the 4f

rare-earth

series because of the combination of a weak crystal ﬁeld and a stronger spin–orbit

coupling that leaves the total angular momentum J largely unperturbed, retaining

most of their orbital and spin degeneracies in a crystal lattice. In some instances, for

example, paramagnetic TmPO

with a degenerate E

doublet ground term from the

partial quenching by the cubic crystal ﬁeld, the distinction between J–T and S–O

stabilization is somewhat blurred. Many observed spin–orbit–lattice effects such as

structural phase transitions induced by a high magnetic ﬁeld are viewed as part of

a broad generic J–T category [42] although spin–orbit effects remain dominant in

other properties such as spin–lattice relaxation.

2.5 Covalent Stabilization

The general topic of chemical bonding is expansive, and its evolution as a prime

vehicle for the application of quantum theory to electronic structure and properties

has grown with the availability and capability of high-speed digital computers. In a

primarily ionic crystal lattice, for example, Na



, the positive cation is bonded

electrostatically to its negative anion neighbors through direct Coulomb forces of at-

traction after the valence electrons of the cation are transferred to the anion. Where

the electronic wavefunctions extend far enough to overlap in the interatomic spaces,

bonding can then be stabilized by attractive forces between electrons and oppos-

ing nuclei, as in the case of the H

molecule. This situation would represent the

purest example of covalent bonding in which the orbiting electrons remain partially

delocalized in their shared orbital states. In an extreme case where the s and p

electrons correlate into itinerant charge clouds that provide the electrostatic “glue”

between the nuclei, the bonding is deﬁned as metallic because the electrons are then

conducting.

2.5 Covalent Stabilization 89

When the metal is from a transition series with unpaired electron spins in or-

bital states that do not participate directly in the bonding, their action is treated as

a perturbation already introduced by the point-charge crystal ﬁeld effects. To probe

the inﬂuence of these unﬁlled shells, hybrid orbital states formed between adja-

cent neighbors must be established. The process therefore involves two approaches

to examining magnetic properties of crystal lattices. To determine the geometrical

structure and bonding energy of the lattice based on ionic and covalent stabiliza-

tion energies, the valence-bond method is used. For the purposes of describing the

electronic origins of the spontaneous effects involving d -andf -shell electrons, an

extension of the crystal ﬁeld or point-charge model called molecular orbital theory

is the most useful method for analyzing local magnetic properties. In this approx-

imation the point charges are replaced by the actual anions (or ligands) and their

orbital states (usually 2p) interact with the d or f states of the transition metal

cations. Analogous to the one-electron model of an individual ion that sorts out

high- and low-spin states by determining the internal spin ordering, molecular or-

bitals can provide insight into the stabilization of interionic magnetic ordering prior

to attempting more elaborate solutions.

2.5.1 Molecular-Orbital Theory

To examine the role of interactions among electrons occupying individual orbital

states of adjacent ions, hybrid orbital states belonging to the overall nuclear skele-

ton of the molecule are constructed from the individual orbitals. In this concept, the

combined orbitals are assigned to the molecule rather than the individual atoms or

ions, and the available bonding electrons among the ions can then be distributed

among these “molecular orbitals” with electron spin directions following the dic-

tates of the Pauli principle and Hund’s rule, analogous to the formation of electronic

conﬁgurations in atomic structure. Once the molecular orbital scheme is established,

the Aufbau principle that was applied to map the electron distributions that make up

the crystal-ﬁeld ground states of the transition-metal ions in Figs. 2.17 and 2.18

can be adopted for the molecule [43]. The particular molecule structure can be

determined a priori from the solution of a valence-bond analysis, with the initial

electronic orbital state energies determined, for example, by a Madelung energy

computation in the case of a well-deﬁned ionic molecule.

In contrast to the valence-bond method that provides information about the

chemical and macroscopic physical properties, including mechanical and thermal

behavior, that are controlled by the strength and geometry of the bonding, a molec-

ular orbital approximation can add a window to the speciﬁc orbital (and electron

spin) interactions that determine the electronic and magnetic properties. This ap-

proach culminates in the formation of hybrid wave functions that describe the

resulting density distributions of the actual charge clouds – hence the term molec-

ular orbitals. It begins with the introduction of covalence in the form of linear

combinations of the atomic orbitals (LCAO) of the individual atoms comprising