Dionne G.F. Magnetic Oxides

Подождите немного. Документ загружается.

60 2 Magnetic Ions in Oxides

Since diagonal elements remains unchanged before and after the perturbation is

applied, for the ﬁve

D orbital states

2."

C "

/ C 3."

C "

/ D 5"

; (2.16)

and it follows that, if "

is arbitrarily set to 0,





D "

D 6Dq;





D "

D4Dq: (2.17)

The value of Dq is determined semiempirically, that is, by experiment, but an ex-

pression for it can be arrived at analytically. As explained in [13],

Dq D˙





for D states

D



315



for F states; (2.18)

where the second signs apply to ions of the lower half of the d

series.

From the eigenfunctions of (2.12) that are plotted in Fig. 2.11, the ordering of

the energy levels can be determined by inspection of the relative positions of the

negatively charged lobes in relation to the negative ligand point charges. Note that

the e

orbitals are directed toward the ligands and therefore will assume the higher

energy states.

From these orbital sketches, the existence of an unquenched l

angular mo-

mentum component may be also discerned. A test for deciding whether an orbital

momentum about an axis can still be present is whether the eigenstate can be trans-

formed into another eigenstate within its degenerate manifold by a rotation about

that axis. In this case of the [001] as axis of quantization, it can be seen by visual

(or analytical) inspection that d

y

rotates into d

by a 45

rotation about z and

that the same applies to d

and d

. Only the latter pairs are eigenstates in a cu-

bic ﬁeld, however, which means that the remaining three states have their l

fully

quenched, including the degenerate e

orbitals. This latter condition will be shown

to be signiﬁcant in the discussion of the Jahn–Teller effect.

If the z axis of quantization is taken as the Œ111 direction, where threefold sym-

metry is prevalent, the appropriate basis vectors may be constructed from the pure

set of (2.6)as

2



1

;

2



1

(2.19)

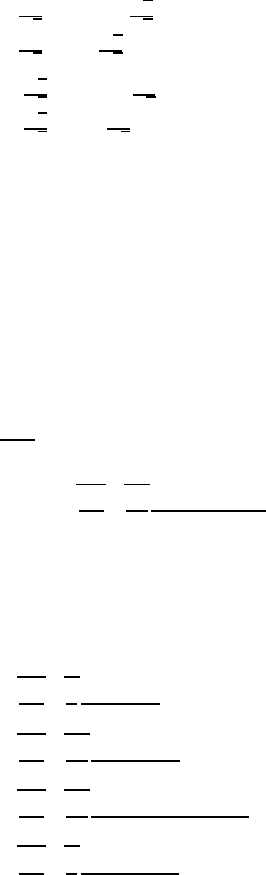
2.3 Crystal Electric Fields 61

As with the earlier eigenfunction set with the z axis along the Œ001 direction, a

straightforward application of the l

operator along the Œ111 direction will verify

that d

and the two e

states have zero angular momentum, while the remaining two

states retain m

D˙1.

By taking linear combinations of the basis vectors in real form from (2.12), we

obtain for D

or C

with the z axis along a <111> direction

e D

y

D e



D e



;

y



D t



D t

(2.20)

The functions of (2.20) are expressed in a coordinate system with z directed along

the Œ111 direction of the cube body diagonal. If an analytical problem that involved

a trigonal or rhombohedral perturbation along the Œ111 axis was to be solved with

this combination of basis vectors expressed in the regular cubic coordinate system

with x, y,andz transformed back into the x

, y

, z

coordinates set up coincident

with the .001/ family of axes, eigenfunctions for this purpose have been reported

by Pryce and Runciman [14] and Dionne and Palm [15].

For this set the appropriate crystal ﬁeld potential energy is given by a relation

[16] analogous to (2.14).



D Y



 Y

3



; (2.21)

where Y

 Y

3

D

4



 3xy



: (2.22)

The second case to be discussed is the three electron

F term, which is of greater

historical importance than the one electron case because it was the basis for the

invention of the maser (microwave ampliﬁcation by stimulated electron radiation).

For this situation the orbital spherical harmonics are the Y

group [12],

3

4

.x  iy/

;

2

4

z .x  iy/

;

1

4

.x  iy/



 r



;

4



 r



; (2.23)

62 2 Magnetic Ions in Oxides

D

4

.x C iy/



 r



;

4

z .x C iy/

;

D

4

.x C iy/

For the F states, the Y

terms of (2.8) must be included in the calculation. Solutions

of the resulting secular equation are a singlet ground state A

and two higher triplets

and T

and those of the inverted case shown in Fig. 2.12, with corresponding

eigenfunctions

3

1

;



3

1



C Y

2



;

; (2.24)





 Y

2





Following the reasoning leading up to (2.14), for

F of d

and

F of d

,theseterm

energies are

D 6Dq;

D2Dq; (2.25)

D12Dq:

Equation (2.24) is a convenient example of the meaning of orbital angular momen-

tum quenching. The ground state is a linear combination of two spherical harmonics

of the l D 2 manifold that yield the singlet A

term under the inﬂuence of the cu-

bic crystal ﬁeld. As such, it has the symmetry properties of a singlet s orbital and

therefore would carry the properties of l D 0; its only contribution to the mag-

netic moment of the ion must come from the ion spin. Conversely, if the orbital

levels are inverted in energy, the triplet T

becomes the ground state and the or-

bital angular momentum would have the characteristics of a degenerate p state with

l D 1. In this case, l is reduced from the d state value of 2 down to 1 and the result

is only partial quenching because not all of the ground state degeneracy has been

lifted. This residual degeneracy is an important factor in the properties of certain

transition 3d

, for example, Co

and a number of 4f

rare-earth ions. Further-

more, where the crystal ﬁeld splitting parameter Dq is small enough to allow the

inﬂuence of the upper terms in a subsequent perturbation calculation, appropriate

2.3 Crystal Electric Fields 63

Table 2.5 3d

states and energies in weak octahedral ﬁelds

d Electrons Orbital ground state

States and energies

in Dq

4

C12

6

2

12

6

4

C12

6

2

12

6

For tetrahedral

coordinations, multiply Dq by 4=9; for cubic

, multiply by 8=9

orbital contributions to the magnetic moment will enter into the eigenfunctions after

spin–orbit and magnetic ﬁeld perturbations are applied.

Recalling the ground state terms of the 3d

series listed in Table 2.4, we can now

point out that the two example solutions for

D and

F will apply equally to the

D and

F cases. Table 2.5 lists these crystal ﬁeld terms for the d

series in units of

Dq, with their signs adjusted to take into account the sign reversal for the upper half

of the series. An insightful commentary on the correspondence and contrast among

these ions was given by Van Vleck [17].

The point charge calculation may also be approached by another powerful tech-

nique called “operator equivalents” developed by Stevens [18]. This method is based

on the replacement of the Cartesian operator functions of the V

potential energy

with the equivalent L or J (whichever is applicable) angular momentum operators.

Expressed in operator equivalents, the ﬁrst part of the D

term of the octahedral ﬁeld

given by (2.7)

oct

D D



C y

C z





D D



C L



L.LC 1/ Œ3L .L C 1/  1



: (2.26)

64 2 Magnetic Ions in Oxides

Since the eigenfunctions of these angular momentum operators are linear combina-

tions of the spherical harmonics, the calculation of matrix elements is straightfor-

ward. Operator equivalents can be very useful for quantitative calculations of more

complex symmetries that involve higher order terms in E

and also for cases of

higher L (or J ) values. An introduction to these techniques is given in Ballhausen

[3]andLow[13] and a more comprehensive discussion including many tables of

matrix elements may be found in Hutchings [16]. To continue with this discussion,

the theory of symmetry groups will be introduced as a powerful tool for ﬁnding

crystal ﬁeld solutions.

2.3.5 Group Theory and Lower Symmetry

Conventional perturbation calculations to determine crystal ﬁeld states can become

arduous for more complicated systems. The solutions for the simple cases outlined

in the previous section will prove almost sufﬁcient for our discussion of the various

magnetic properties. To cope with the frequently encountered trigonal, tetragonal,

and orthorhombic distortions of the cubic coordinations, however, the solutions are

found by a shortcut that is derived from symmetry considerations. In the point

charge calculations, diagonalization of matrices by solutions of higher order sec-

ular determinants may be accomplished by applying group theory to determine not

only the best linear combinations of wavefunctions but also the degeneracies of the

different eigenstates, for example, the A

, E

, T

,andT

terms of the type de-

ﬁned by (2.21).

Unfortunately, the scope of this text will not permit a detailed exposition of group

theory. The interested reader is directed toward any number of excellent treatments

of this subject, including those cited earlier [3–5, 19]. For the purposes at hand,

we need to recognize that the diagonalization process involves the construction of

wavefunction combinations that conform to the symmetry of the perturbation oper-

ator. Group theory provides a method for predetermining the correct eigenfunction

combinations for a particular perturbation problem and is useful in solving for the

eigenfunctions of lower symmetry ﬁelds.

There are some terminologies that should be mentioned because they will re-

cur throughout this volume. Energy levels or eigenvalues are often referred to as

irreducible representations or energy terms. Their corresponding eigenfunctions are

called basis vectors. Early development of this discipline was conducted by Bethe

[20] and Mulliken [21], and two nomenclatures of the representations have sur-

vived, although the Mulliken version seems to have gained some preference. It has

already been introduced in the designations of the spherical harmonic combinations

in (2.24). Table 2.6 lists the notations for these two systems with the corresponding

degeneracies. The results of group theory analysis of the crystal ﬁeld problems have

been well documented, and the cubic ﬁeld representations for the various orbital

terms are summarized in Table 2.7.

For the simple case of a descent in symmetry from cubic O

to tetragonal D

orthorhombic D

, the relation of the basis vector lobes to the changing locations

2.3 Crystal Electric Fields 65

Table 2.6 Comparison

of Mulliken and Bethe

representation notations

Mulliken Bethe Degeneracy



E



1=2



5=2



G

Table 2.7 Irreducible representations for cubic symmetry

Ground Term l Mulliken Bethe

S0A



P1T



D2E C T



C 

F3A

C T



C 

G4A

C E C T

C T



C 

C

H5E C 2T

C T



C 2

C 

I6A

C A

C E C T

C 2T



C 

C

C 2

Fig. 2.13 Comparison of d -electron energy levels in crystal ﬁelds of tetragonal .c=a < 1/ and

trigonal

˛>60

symmetries [15]

of the negatively charged ligands can be visualized in Fig. 2.11. For a tetragonal

distortion shown in Fig. 2.6c, T

,andd

/ splits in the same way as the

trigonal case, but the upper E

doublet is now also split because of the relation of

the d

y

and d

lobes to the octahedral ligands. The orthorhombic distortion D

of Fig. 2.6d will remove the ﬁnal degeneracy and split the d

and d

states. The

splittings of the orbital D term in these axially distorted cubic ﬁelds are compared

in Fig. 2.13.

66 2 Magnetic Ions in Oxides

The energy level structure for the special cases of the tetragonal or orthorhom-

bic distortions that occur with pyramidal O

and planar O

coordinations shown in

Fig. 2.7 may be inferred by extrapolating the results for the weak ﬁeld solutions.

The descent in symmetry from cubic to the planar structure is particularly important

in the cuprate superconductors to be examined in Chap. 8. To obtain a quantitative

sense of the inﬂuence of a strong tetragonal ﬁeld, we return brieﬂy to the point

charge calculation and examine the effects of a tetragonal component V

to the oc-

tahedral crystal ﬁeld energy H

 V

octCT

D V

oct

C V

,where[22]

D f

.r/ R .r/ Y

C f

.r/ R .r/ Y

; (2.27)

where f

.r/ and f

.r/ are radially-dependent coefﬁcients. With the eigenfunction

set of (2.11), diagonal matrix elements may be obtained by straightforward integral

computations. Part of this process involves the deﬁning of two additional splitting

parameters representing the integrals of the radial components of the respective ma-

trix elements over space, according to

Ds D

ŒR .r/

.r/ d;

Dt D

ŒR .r/

.r/ d: (2.28)

From this deﬁnition, it may be shown that the energy states of the tetragonal pertur-

bation follow directly from the diagonal matrix elements. The splitting of the upper

doublet E

of the O

C D

group becomes



y

oct

C V

y

D 6Dq C 2Ds  Dt;



oct

C V

D 6Dq  2Ds  6Dt: (2.29a)

and that of the lower T

triplet is



oct

C V

D4Dq C 2Ds  Dt;



xz;yz

oct

C V

xz;yz

D4Dq  Ds C 4Dt: (2.29b)

where the lowest d

and d

orbitals retain their degeneracy. For Ds and Dt > 0,

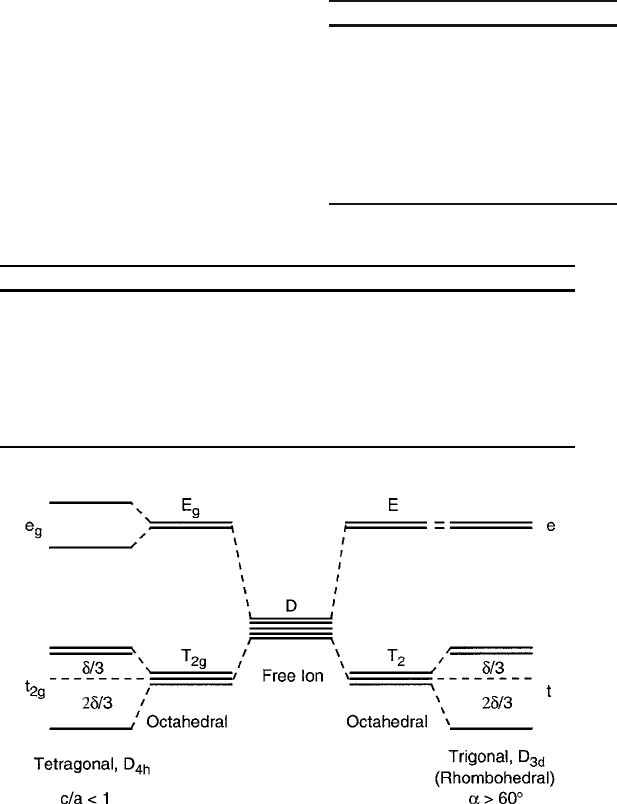
the order of energy levels is shown in Fig. 2.14. As drawn, the structure is shown

with the doublet as the ground state, but this may not necessarily be the case since

the relative individual values of Ds and Dt would determine the correct order. Note

that the uppermost state is still d

and that it reaches a maximum separation of 10Dq

from the next highest state, which is now d

instead of d

. The crossover point

where this upper state splitting becomes equal to 10Dq can be attained with a large

tetragonal distortion, but may not necessarily require a complete removal of the two

apical ligands along the z axis that would leave only an O

planar coordination. This

point is discussed further in relation to the superconductivity of cuprates in Chap. 8.

2.3 Crystal Electric Fields 67

Fig. 2.14 Details of orbital energy level splittings as a tetragonal crystal evolves from cubic to

planar, showing the 10Dq destabilization of the highest e

level. Diagram is based on Fig. A.47 of

[4]

Another demonstration of energy level determinations by group theory is real-

ized by the descent in symmetry from O

! D

that is commonly encountered in

magnetic oxides. From the basis vectors for a trigonal distortion of an octahedral

site reveal that the lower triplet T

is split into a doublet and a singlet, while the

degeneracy of the upper doublet E

is unchanged, as shown in Fig. 2.13. The fact

that the upper doublet remains degenerate will be shown to be important in a later

discussion of the Jahn–Teller effect.

For a trigonal distortion, the crystal ﬁeld potential energy isV

octC£

D V

oct

C V

where V



is applied in a similar fashion to that of the tetragonal ﬁeld component

given by (2.27), except that the set of orbital functions that it operates on are the

group of (2.20). Upon application of this perturbation, the matrix elements are

oct

C V

D 6Dq C

D;

oct

C V



D4Dq C D C

D;

68 2 Magnetic Ions in Oxides

oct

C V

D4Dq  2D  6D; (2.30)

oct

C V

2D 

D:

where D and D are deﬁned analogously to Ds and Dt of (2.28).

At this point it is instructive to compare (2.29)and(2.30). The tetragonal and

trigonal cases are similar in that the T

(and T

) group is split into a singlet and

doublet, but as illustrated in Fig. 2.13,theE

(and E) term remains degenerate in

the trigonal ﬁeld. Moreover, we now see that the t

and e

states mix under the V

perturbation. Pryce and Runciman [14] have studied this question in detail, but for

our purposes, we assume that D.5=3/ D and that the off-diagonalelements are

negligible, so that the matrix may be approximated as diagonal in later discussions.

2.3.6 Strong Field Solutions and Term Diagrams

If the crystal ﬁeld is strong enough to compete with the mutually repulsive inter-

actions among orbiting electrons in ions with multiple d electrons, or if the crystal

ﬁeld inﬂuence on the excited terms is important, all of the terms listed in Table 2.4

must be included as part of any thorough perturbation calculation. This situation is

encountered in cases where the crystal-ﬁeld splitting is larger, for example, for cer-

tain ligands such as the cyanide radical CN

, or with the larger radii 4d

and 5d

ions. The most common need for the full energy term diagrams occurs in the inter-

pretation of optical transitions from the ground state, as discussed in Chap. 7.Al-

though the ground term is usually the only part of the free-ion energy level structure

that is needed to explain the properties of magnetic oxides, the reader should appre-

ciate the meaning of the term diagrams and the basis of their theoretical origins.

If the procedure outlined for the weak ﬁeld is extended to include the upper terms

in the conventional way, large matrices result and solutions to the complete term

picture must be worked out by solution of the corresponding equations, simpliﬁed

wherever possible by the use of group theory and any other methods for reducing

the complexity of the matrices. To this end, Orgel [23] reported matrices and com-

putations for the d

series expressed in terms of the single parameter Dq. His results

for the important d

case of Fe

or Mn

(symmetric in sign for any of the cubic

coordinations in this particular instance) are shown in Fig. 2.15.

An alternative approach to the strong ﬁeld problem is to consider the effects of

the ligands on the orbital electrons prior to the energy of their mutual interaction

term

that determines the free-ion term splittings, that is, the intra-atomic e

repulsive energies. It is then assumed that the distributions of electrons among the

d orbital states are determined ﬁrst by the repulsive forces of the ligands, with the

mutual interactions among the electrons treated as the perturbation. In this situation,

the starting energy states are no longer inﬂuenced by Hund’s rule of orbital ordering,

but rather by the various electron distributions among the t

and e

orbital states as

dictated by the crystal ﬁeld, in this case anticipated as octahedral.

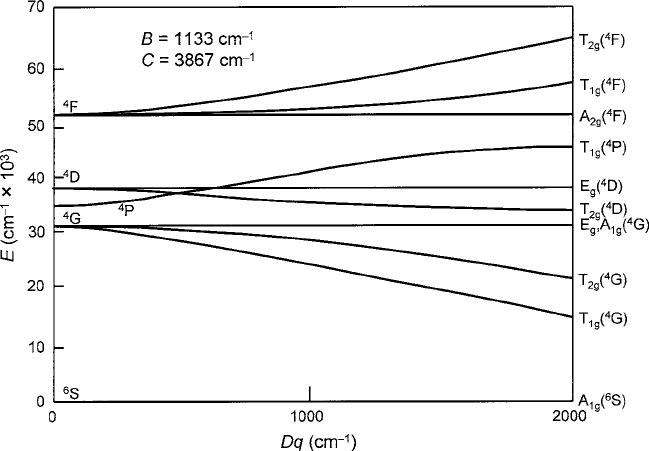
2.3 Crystal Electric Fields 69

Fig. 2.15 Multielectron energy level term diagram for a 3d

ion in an octahedral crystal

ﬁeld of O

2

ligands. Author’s computations were based on the model of Orgel [24]

In the strong ﬁeld limit, it is assumed that the mutual repulsion among the elec-

trons in the ligands dominates the distribution of electrons among the d orbital

states. As a consequence, the system of free-ion terms is broken down, and the

energy states are selected according to occupation numbers of electrons in the t

and e

shells, ﬁrst by ﬁlling the lower t

levels and then the less stable e

states.

For the simplest multiple electron case of two d electrons, there are three possible

orbital conﬁgurations within the octahedral Dq separation,













,and





. Within each of these distributions are many possible combinations that are

set by number of electrons and the number of individual states [24]. The respec-

tive energies of these groups of states is given to a ﬁrst approximation by assigning

4Dqto each electron in a t

level and C6Dq to the remaining e

electrons. To

complete the calculation, the mutual repulsion energies, which separate the free-ion

term energies through the E

rep

perturbation, are recalculated based on mixtures of

the speciﬁc octahedral t

and e

wave functions of (2.12) and then added as com-

binations of K (Coulomb) and J (exchange) determinant element integrals in the

manner of those introduced previously in relation to interatomic electron repulsion

in Sect. 1.3.3. As an example calculation, consider the interaction between the d

and d

orbitals of (2.12), for which the elements (of the Slater determinant) are

simply stated from the deﬁnition in Ballhausen [25]: