Dionne G.F. Magnetic Oxides

Подождите немного. Документ загружается.

40 2 Magnetic Ions in Oxides

2.1.2 Iron Group 3d

Ions

In the periodic table of Fig. 2.1, the elements with ions that produce signiﬁcant

magnetic effects in combination with oxygen are distinguished by shading. Their

common feature is an incomplete inner d

of f

shell. In general, the atoms sur-

render their outer s electrons to form ionic bonds with atoms that accept them to

complete their own unﬁlled s and p shells. In an analogy to electron tubes with a

cathode (emitter) and anode (plate), the metal atom that donates electrons is called

a cation, while the “anode” atom becomes an anion. Because oxygen normally has

an anion valence of 2, the cations formed from the transition metals usually have

valence charges of at least 2C, particularly in the complex oxide compounds that

produce the magnetic properties of practical interest.

One immediate observation is that once the outer 4s electrons are stripped from

the iron group elements, the partially ﬁlled 3d

shell is exposed to the molecular

environment, which is a crystal lattice of speciﬁc symmetry comprising electric and

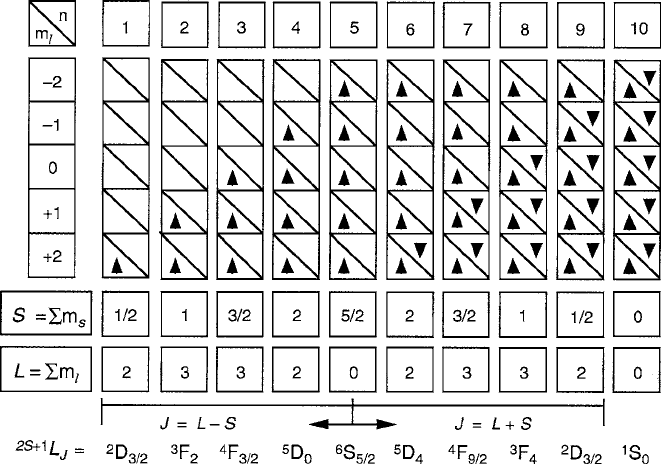
magnetic ﬁelds of its own. Figure 2.3 is a diagram of the electron occupancy of the

ten d states (two for each of the ﬁve orbitals in compliance with the Pauli exclusion

principle), indicating the formation of the multi-electron L, S,andJ quantum states

for each ground term based on Hund’s rules. The relevant parameter data for the iron

group are summarized in Table 2.1.

The ions of the lower third of the group 3d

, 3d

,and3d

are generally para-

magnetic and exhibit little collective properties, usually only causing perturbing

Fig. 2.3 Application of Hund’s rule in the formation of angular momentum ground terms in the

shell. Terms are either D

L D 2

L D 3

,orinthe3d

case, S

L D 0

2.1 The Transition Metals 41

Table 2.1 Parameters of the iron group 3d

ion series in oxygen sites

Ground state Radius

2

Electrons Ion Term LS J (

A) n Remarks

0 0 0 0.73 6 Diamagnetic ion

3=2

2 1/2 3/2 0.67 6 Metallic with

,forms

blue sapphire

in Al

3C 3

3120.64 6 Largeion

0.86 6

3=2

33/23/20.61

0.54

Forms red ruby

in Al

2200.82

0.65

J–T ion, magne-

tostrictive.

metallic with

5=2

05/25/20.82

0.64, 49

6, 4

S-state ion,

low-spin

S D 1=2

2240.77

0.61

Magnetostrictive,

low-spin

S D 0

9=2

33/29/20.73

0.60

Spin–orbit

stabilized,

highly

anisotropic,

fast-relaxing,

low-spin

S D 1=2

3140.70

Magnetostrictive

low-spin

S D 0

5=2

2 1/2 5/2 0.73 6 J–T ion, magne-

tostrictive,

metallic

conductor

with S D





0000.96 6 large

diamagnetic

ion, metallic

with Cu

Based on radius of divalent oxygen of 1.40

J.B. Goodenough, G. Demazeau, M. Pouchard, and P. Hagenm¨uller, Solid State Chem. 8, 325

(1973)

42 2 Magnetic Ions in Oxides

effects on the remainder of the series. The magnetic moments of ions from 3d

through 3d

are capable of producing strong spontaneous magnetism when in sufﬁ-

cient densities to allow exchange coupling to the order magnetically as ferro-, ferri-,

or antiferromagnets. In all cases where the ion is chemically bonded in an anion

lattice, the combined orbital angular momentum L is uncoupled from the spin S by

the electrostatic ﬁelds of the lattice, and the spin moments dominate the magnetic

properties. Where this occurs J is no longer a meaningful quantum number. Conse-

quently, the spectroscopic g factor is approximately equal to 2 for the spin angular

momentum of a free electron in all but a couple of special situations.

2.1.3 Rare Earth 4f

Ions

The second most important transition group from a magnetic standpoint has an un-

ﬁlled 4f

shell. These elements are commonly referred to as the rare earths or

lanthanides because La is the ﬁrst member of the series. The higher group with un-

ﬁlled 5f

shell, called the actinides also has magnetic properties. As mentioned

earlier an important distinction between the 4f

ions and those of the 3d

iron

group is the shielding of the 4f shell inside the 5s

and 5p

outer shells of the Xe

core. In other words, the magnetically active electrons are buried inside the Xe core

and are therefore shielded from electrostatic ﬁelds of the molecular environment. As

a result, the ions act largely independent of one another, even in highly concentrated

compounds, and are generally paramagnetic because the multiple lobes of the 4f

orbital wavefunctions do not extend far enough for covalent bonding and magnetic

exchange to be signiﬁcant.

Inspection of Table 2.2 reveals that the J values of the ions are divided into a

lower and upper group, based on whether L is larger or smaller than S . Following

Hund’s rule, for the lower half from Ce

to Eu

, J DjL  Sj; the upper half

from Gd

to Yb

features larger spin values, i.e., J DjL C Sj. It will become

evident later that the J values of the rare earths are the important angular momen-

tum parameters because of strong spin–orbit coupling energies. Consequently, the

g factors also are heavily dependent on J through the L contribution. As computed

from (1.18), the g factors listed in Table 2.2 are exclusively less than 2. Rare-earth

ions contribute a number of important effects that include the tailoring of magne-

tization vs. temperature behavior in magnetic garnets, the control of high-power

properties of microwave ferrites, and the Faraday rotation of magnetic garnets and

other compounds for optical applications.

2.1.4 4d

and 5d

Ions

The unﬁlled 4d and 5d shells of the other two transition series have ions that resem-

ble the 3d series in magnetic properties and can be used as alternatives for them in

certain cases. Tetravalent ruthenium





with a 4d

conﬁguration, for example,

2.2 Oxygen Coordinations 43

Table 2.2 Parameters of the rare earth 4f

ion series

Ground state Radius

Electrons Ion Term LS J g (

A) Remarks

0 0 0 – 1.18 Diamagnetic ions

0.97

5=2

3 1/2 5/2 6/7 1.14 Strong magneto-

optical

properties

0.99

5 1 4 4/5 1.14 Strong magneto-

optical

properties

9=2

6 2 4 8/11 1.12 Strong magneto-

optical

properties

6 2 4 3/5 0.98 Synthetic

element

5=2

5 5/2 5/2 2/7 1.09 –

3 3 0 – 1.07 Diamagnetic ion

7=2

0 7/2 2 2 1.25 S-state ions

1.06

3 3 6 3/2 1.04 Fast-relaxing ion

15=2

5 5/2 15/2 4/3 1.03 Fast-relaxing ion

6 2 8 5/4 1.02 Fast-relaxing ion

15=2

6 3/2 15/2 6/5 1.00 Fast-relaxing ion

5 1 6 7/6 0.99 Fast-relaxing ion

7=2

3 1/2 7/2 8/7 0.98 Fast-relaxing ion

0 0 0 – 0.97 Fast-relaxing ion

Based on an oxygen coordination of 8

Lutiteum is included here to complete the 4f shell. It also represents the beginning of the 5d

series

has magnetoelastic properties similar to those of trivalent manganese





with

a 3d

occupancy. In general, these ions have not attracted much interest for their

magnetic properties because the compounds formed from them do not exhibit strong

spontaneous magnetic properties. Moreover, several of them, such as rhodium (Rh),

palladium (Pd), osmium (Os), iridium (Ir), and platinum (Pt) are not available in

sufﬁcient abundance to be considered for low-cost applications. Intermetallic com-

pounds of niobium (Nb), however, have found important uses as superconductors.

2.2 Oxygen Coordinations

Transition metal ions are chemically reactive and occur naturally bonded to anions

of the seventh or eighth columns in compounds that are made up of distinct crystal

structures. Such compounds can be viewed as comprising separate metal (cation)

44 2 Magnetic Ions in Oxides

and anion lattices. In the discussions to follow, emphasis is placed on the immediate

surroundings of the metal ions, speciﬁcally the disposition of the oxygen or ligand

coordinations relative to the transition ion.

2.2.1 Crystal Systems and Point Groups

The subject of crystallographic symmetry is important to the study of magnetic

oxides, and a brief review is essential for the understanding of the concepts that

determine the properties of the transition ions in oxygen coordinations. For a thor-

ough treatment of the subject the reader is referred to the more general literature and

text books [1, 2]. In this text, the focus is on the crystal ﬁeld and molecular orbital

theories by which most of the magnetic-related properties are examined.

Table 2.3 lists the seven systems that comprise all the naturally occurring types of

crystalline structures. Corresponding cell sketches are presented in Fig. 2.4.These

systems are in turn composed of 32 crystallographic “point groups” or crystal

classes, which describe the basic symmetry of crystallographic building blocks or

unit cells. A point group, therefore, consists of a collection of symmetry opera-

tors that serve to deﬁne particular crystal structures. There are three such basic

operations: rotation, whereby the structure repeats itself upon rotation around a par-

ticular direction or axis, for example, fourfold meaning that it repeats the image of

its projection along the axis every 90

, reﬂection about a plane, and inversion, mean-

ing that the crystal retains its appearance after undergoing reversal of each of the x,

Table 2.3 Crystal systems and their symmetry elements

System

Generic point

group

Unit cell Symmetry

Triclinic – a ¤ b ¤ c

˛ ¤ ˇ ¤  ¤ 90

No axes, no

planes

Monoclinic – a ¤ b ¤ c

˛ D ˇ D 90 ¤ 

One twofold axis

or one plane

Orthorhombic D

a ¤ b ¤ c

˛ D ˇ D  D 90

Three orthogonal

2-fold axes

two planes

intersecting a

2-fold axis

Tetragonal D

a D b ¤ c

˛ D ˇ D  D 90

One 4-fold axis

or a 4-fold

inversion axis

Rhombohedral (trigonal) D

a D b D c

˛ D ˇ D  ¤ 90

One 3-fold axis

Hexagonal D

Three axes a in

x  y plane

at ˛ D 120;

c ¤ a

One 6-fold axis

Cubic (isometric) O

a D b D c

˛ D ˇ D  D 90

Four 3-fold axes

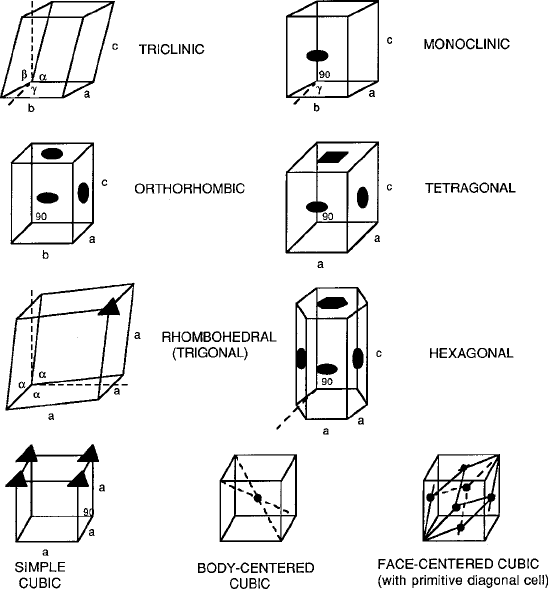
2.2 Oxygen Coordinations 45

Fig. 2.4 Crystal system diagrams

y,andz coordinates. An even further reﬁnement categorizes the point groups into

240 “space groups,” but this level of detail will not be necessary for the purposes of

this text.

There will be no attempt to explain in detail the nomenclature of the point groups

beyond the occasional labeling of particular structures for identiﬁcation purposes.

For the scope of this text, the rotation operators will be sufﬁcient to designate the

symmetries that will be encountered.

2.2.2 Cubic Symmetry

In the magnetic oxides of interest in this text, the cations usually reside in lattice

sites comprising oxygen arrangements referred to as coordinations. The basic unit of

building block is generally of cubic (isometric) symmetry or one that is derived from

it. In Fig. 2.5 the most common situations are sketched in relation to the orthogonal

Cartesian axes and are of four types: tetrahedral, with four sides and four anions

on alternate corners as shown; octahedral with eight sides and six anions on the

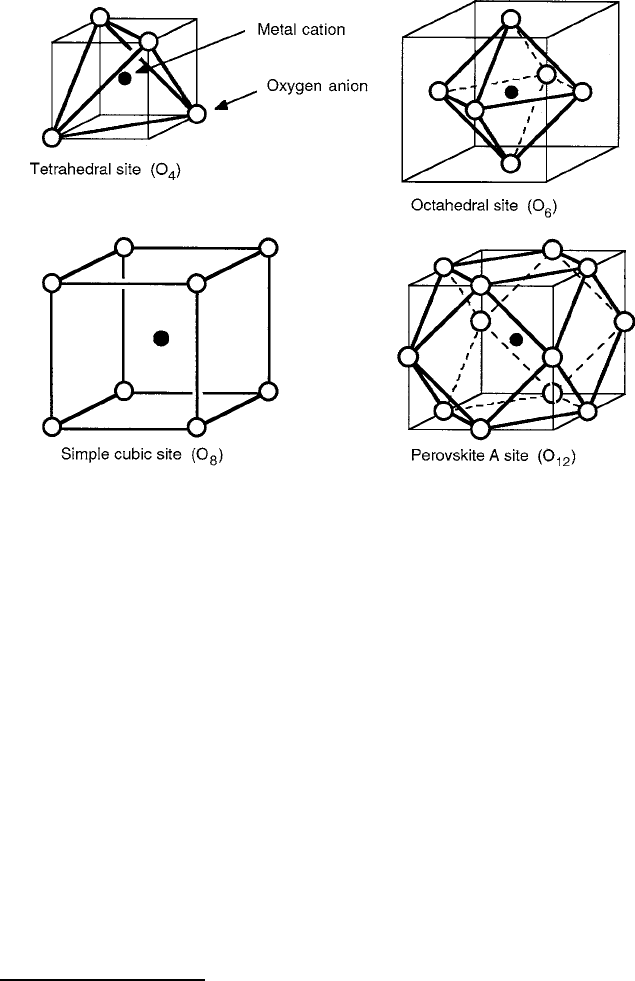
46 2 Magnetic Ions in Oxides

Fig. 2.5 Cation sites with ligand coordinations of cubic symmetry

corners of an octahedron formed with anions at the cube face centers; simple cubic

with six sides and eight anions at the cube corners; and dodecahedral, with 12 sides

and 14 anions located at the eight corners of a half-sized cube and six more at the

face centers of the full cube. This latter structure does not actually occur in the

magnetic oxides of interest here. In reality the “dodecahedral” site of the garnets

is a 12-sided cell formed from a twisted cube with only eight corner anions. Each

of these coordinations can have the required four threefold symmetry axes directed

along body diagonals, referred to as the <111> family according to the convention

of the Miller indices.

The corresponding indices for the three fourfold cubic axes

(along x, y,andz directions) are the <100> family and for the face diagonals, it is

the <110> family.

The most common oxygen coordination is octahedral, here labeled as O

for the

six anions. The octahedral site is of paramount importance in spinels, garnets, and

the various perovskite-related compounds. The tetrahedral coordination, designated

, is the alternate cation site in the spinels and garnets and is generally occupied by

smaller metal ions. Because the smaller separation between anions leads to higher

The Miller indices were developed to identify the various planes in a crystallographic lattice. The

system is based on the values of the three intercepts of the plane with the x, y,andz axes expressed

as the lowest integer values. The labeling convention for family of planes is fhklg and an individual

plane is (hkl). Alternatively, the normal axes to the planes are labeled < hkl > for the family and

[hkl] for an individual axis.

2.2 Oxygen Coordinations 47

mutual repulsive forces, the higher coordination numbers result in larger site vol-

umes to minimize these bonding energies. For this reason the larger ions, such as

the lanthanide rare earths, usually occupy O

as in the cubic perovskites, or the

dodecahedrally distorted O

sites in the garnets.

2.2.3 Lower Symmetries

In all but the simplest oxides, the cubic symmetry is usually reduced by lattice

distortions that are often large enough to be considered as part of a phase transi-

tion to another point group even though the effect may be local and involving only

an isolated cation complex. Even when the distortions are subtle, their effects on

the magnetic properties can be signiﬁcant. Since the issue of lattice distortions and

symmetry changes will recur regularly throughout the balance of the text, it is ap-

propriate that it be introduced in an orderly manner.

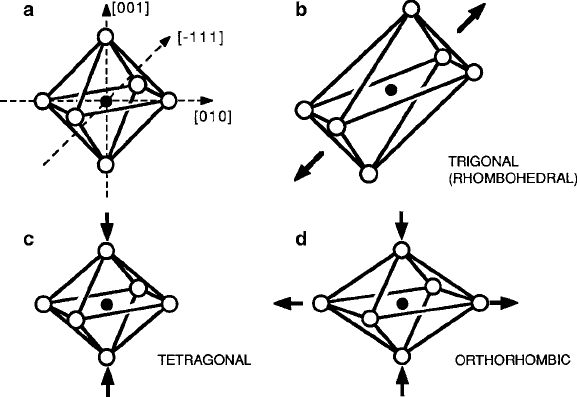
Departures from cubic symmetry vary from slight to catastrophic. However, there

is no immediate need to discuss more than the few that are depicted in Fig.2.6.

The most convenient vehicle to examine these distortions is the octahedral site,

which may undergo extensions or compressions along any of the principal axes

of symmetry. In most cases, the <111> and <100> groups shown in Fig. 2.6aare

the ones of concern. If the distortion is along a <111> axis as pictured in Fig. 2.6b,

the symmetry is reduced form cubic O

to trigonal or rhombohedral D

or C

and the immediate environment of the cation has one threefold symmetry axis.

Figure2.6c, d indicates the effects of a tetragonal D

compression along the [001]

axis and then the addition of a second distortion, this time an extension along the

Fig. 2.6 Cubic cation sites with simple distortions

48 2 Magnetic Ions in Oxides

Fig. 2.7 Other ligand coordinations in oxides

[010] axis to create a lower orthorhombic D

symmetry. Combinations of trigo-

nal and tetragonal distortions that can occur through spontaneous local distortions

called Jahn–Teller effects can reduce the symmetry even further, as will be described

in Chap. 5.

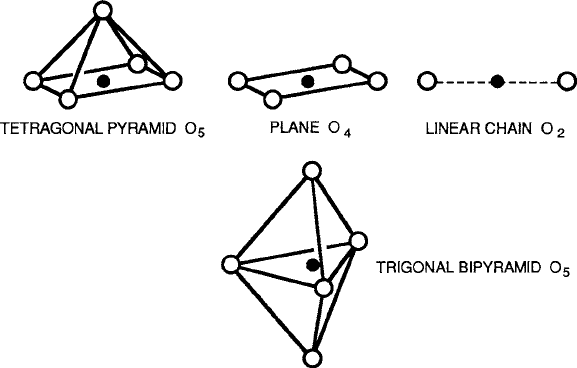
There are four other situations that are commonly encountered in magnetic ox-

ides, shown in Fig. 2.7. A tetragonal pyramid, which occurs when one of the z-axis

oxygen ions is missing, provides an O

coordination of C

symmetry (no reﬂec-

tion plane in this case); a square or rectangular planar conﬁguration is formed

by the removal of both dihedral anions and provides the ultimate tetragonal or

orthorhombic D

or D

symmetry, and a one-dimensional chain that remains af-

ter two opposite planar oxygens are removed gives pure cylindrical symmetry. In

recent years, these abbreviated octahedra have been detected in the superconduct-

ing layered perovskite-type compounds. A fourth cation site takes the form of a

trigonal bipyramid and occurs in the hexagonal structure originally called “mag-

netoplumbite.” This site occurs as only one of 13 in the type-M hexagonal ferrite

compounds and is a strong contributor to the highly anisotropic properties of these

important compounds.

2.3 Crystal Electric Fields

For an ionic lattice, the site of the cation can be approximated by an electrostatic

trap formed by a “cage” of anion neighbors. If a “point charge” approximation is

used for both the cation and the coordination of anions, the stabilization energy of

2.3 Crystal Electric Fields 49

the cation relative to free space is determined by the strength of the resulting ionic

bond. When the electrons orbiting the cation nucleus are considered, the separate

states of a degenerate orbital term are split by the perturbation in the manner of a

Stark effect, which typically amount to about 10% of the lattice bonding energy,

depending on the relative proximities of the various wavefunction lobes to the anion

charges. This perturbation ﬁeld from the anion coordination is called the crystal

ﬁeld. When the orbital wavefunctions of the anions are taken into account, the point

charges are elevated to the status of ligands, and the eigenfunctions of the orbital

states are hybridized to include both cation and anion contributions. The crystal-

ﬁeld model then forms the basis of ligand ﬁeld theory that in turn serves as the

foundation for the molecular-orbital concepts described in later sections.

Although the bonding is principally ionic in oxide compounds, the smaller cova-

lent component is critically important for the electronic and magnetic properties of

compounds with cations of a transition series. To analyze states of an ion for which

the orbiting d electrons interact with the negative charges of the anion coordination,

the effects of point-charge crystal ﬁelds on orbital angular momentum of the cation

are examined ﬁrst.

2.3.1 Angular Momentum States

To introduce the quantum mechanical effects of Stark splittings to the free ion orbital

angular momentum states, it is necessary to review the formation of the multielec-

tron orbital terms that are usually governed by Hund’s rules, which state that the

lowest energy multiplet term has the following:

1. The maximum possible combined spin value S,and

2. Within the maximum S manifold, the maximum combined L.

These rules originate from the Pauli exclusion principle and the quantum mechanical

necessity for spins to align parallel when dispersed among the set of orthogonal

orbital wavefunctions by mutual electrostatic repulsion. To visualize the “laddering”

exercise, Fig. 2.3 illustrates schematically the situation among the states of a d

series. The rows of stacked boxes represent an orbital angular momentum value

of operator l

. Each box can hold two electrons, one for each up or down spin

orientation as required by the Pauli exclusion principle. Beginning with the lower

half of the series from d

to d

, the electrons are added sequentially, obeying the

spin polarization requirement to ﬁll the ﬁrst ﬁve up spin compartments and produce

a half-ﬁlled set of orbitals with the maximum spin value of S D 5=2 when the d

limit is reached.

From an energy standpoint, the half-ﬁlled shell is most stable because each d

electron occupies a separate orthogonal orbital state, and the destabilizing effect of

the mutual repulsion is a minimum. This correlated spatial dispersal of the polarized

spins beyond a random distribution reduces the screening of the nucleus and stabi-

lizes the spins in proportion to their numbers (or their combined S). As the upper