Dionne G.F. Magnetic Oxides

Подождите немного. Документ загружается.

1.2 Induced Magnetism 9

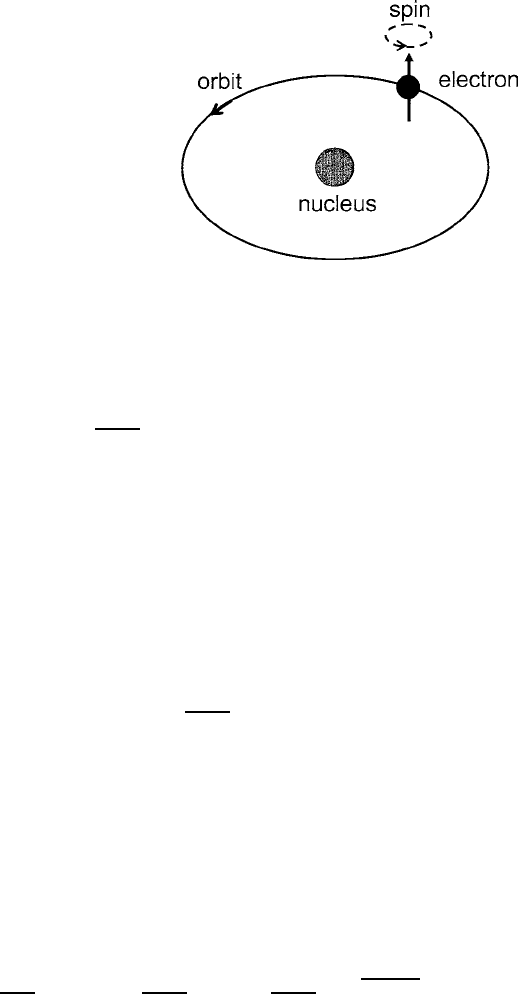
Fig. 1.3 Atomic origins of

the orbital and spin magnetic

moments

a nucleus, as pictured in Fig. 1.3. The most basic quantity in electronic magnetism

is the magnetic moment of the electron spin m

, called the Bohr magneton, which

is deﬁned from the principles of electrodynamics as

e„

D 9:27  10

21

.emu/: (1.20)

[For a proton, a much smaller nuclear magneton is similarly deﬁned as m

, with

mass D 1; 836 m

.] Although electric charges can be distinguished by a sign dif-

ference, in neglect of rigor we shall adopt the commonly used convention that e is

positive unless otherwise required.

A vital concept that also arises from quantum mechanics is the relation between

magnetic moment and angular momentum. For the electron spin, the angular mo-

mentum along the z-axis of quantization is deﬁned from the uncertainty principle as



D˙„=2 and it follows from (1.20)that

D g







; (1.21)

where g (D2 for an electron spin) is the Land´e or spectroscopic splitting factor

(of historical signiﬁcance in connection with the discovery of the Zeeman effect).

Note that Planck’s constant is contained in 

. This line of reasoning can extend

to the orbital angular momentum through a simple classical analogy of a current

loop formed by the electron in an orbit of radius r and angular frequency ! that

constitutes a current i D e!=2c encompassing a circular area A D r

with or-

bital angular momentum l D m

!. Here, the individual orbital magnetic moment

becomes

D iA D



2c



r

D g





l D g





.l C 1/„; (1.22)

where g D 1 for orbital magnetism and Planck’s constant is contained in l.Itis

therefore appropriate to adopt the notion that the magnetic moment of a free atom

10 1 Introductory Magnetism

or ion is directly proportional to its angular momentum and the effective g factor,

which varies between 1 and 2 depending on the relative weighting of the orbital and

spin contributions.

In the many-electron systems of atoms and ions, the angular momenta of spins

and orbits are added as scalars, provided the rules of the Russell-Saunders coupling

are observed. From the standard theory of the addition of angular momentum, the

squares of the resultant angular momenta expectation values of S for spins and L

for orbits summed over all of the electrons in a particular orbital shell are related by

D S.SC 1/ „

;

D L.LC 1/ „

; (1.23)

where S D

s, with s D 1=2 and L D

l, with l D 0,1,2,3,etc.forthe

s, p, d ,andf shells, respectively. The values of S range from a maximum S and

descend in steps of 1 to a minimum of 0 or 1/2 depending on whether the number

of electrons is even or odd, that is, S , S  1, S  2;:::;1=2or 0. The values of L

follow the same rule except that the minimum can only be 0 because of the integer

values of l.

Of particular importance for the rare earth elements is the total angular momen-

tum J , which is formed by the coupling of S and L vectors and is given by

D J.JC 1/ „

; (1.24)

where J

D L

C S

C 2L  S ,andJ may assume values from a maximum of

L CS

L  S

, again in steps of 1, thereby creating a multiplicity of values

(2S C 1). Note that the spin–orbit coupling operator can be expressed as

L  S D

ŒJ .J C 1/  L.LC 1/  S.SC 1/ „

: (1.25)

Apart from the quantum mechanical operators S

, L

,andJ

, the other group of

diagonal operators are the z-components of these momenta M

„, and their values

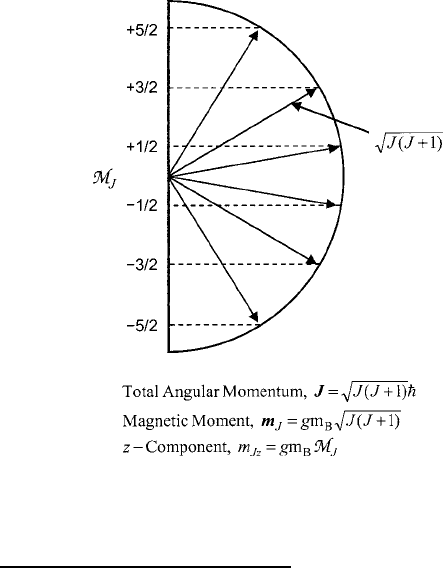
can be observed by the spatial quantization model of Fig. 1.4 for S D 5=2,where

can take values from CJ to J , with a multiplicity of 2J C 1. In magnetism,

the z component represents the measurable or observable quantity and is therefore

of critical importance. From these basic relations, it is now possible to construct

general expressions for the total magnetic moments from a set of S , L,andJ

vectors with Planck’s constant assumed by the Bohr magneton (1.20):

D g





J.J C 1/„Dgm

J.J C 1/; (1.26)

and

D g





„Dgm

; (1.27)

1.2 Induced Magnetism 11

Fig. 1.4 Spatial quantization

diagram of the total angular

momentum for J D 5=2.

Note that Planck’s constant

becomes absorbed in the

Bohr magneton m

when the

magnetic moment is deﬁned

where

g D 1 C

J.J C 1/ C S.SC 1/  L.LC 1/

2J .J C 1/

: (1.28)

1.2.2 Temperature Dependence of Susceptibility

Except for the paramagnetism of a free-electron gas in metals (Pauli paramag-

netism), which is temperature insensitive to ﬁrst order, the most characteristic

feature of paramagnetism is the inverse temperature dependence of the suscep-

tibility. The derivation of the functions describing this dependence is born out

of classical Boltzmann statistics, which are applicable provided that interactions

between the individual moments are negligible. Note that the small diamagnetic

component remains part of the total induced susceptibility.

Consider a collection of n independent identical magnets of moment m per unit

volume subjected to a magnetic ﬁeld H .AtT D 0K, the moments may be expected

to align with the ﬁeld without perturbation. At higher temperatures, randomization

due to thermal agitation from lattice vibrations would work against the magnetic

alignment. The resultant effective magnetic moment would be less than nm by a

factor that varies directly with H and inversely with T .

12 1 Introductory Magnetism

Langevin ﬁrst solved this problem from an entirely classical standpoint by

assuming that (1) m is the only value of magnetic moment possible, (2) all direc-

tions of m are allowed, and (3) the only aligning agent is H . The reduction in energy

from the interaction between a moment m forming an angle  with z-axis-directed

H vector is

DmH cos : (1.29)

The ratio of the effective z component of the total magnetic moment to the actual

moment is determined by integrating over the continuum of energy states weighted

by the Boltzmann occupation probability exp .E

=kT/ covering the complete

range of  values. The weighted average of the moment in the direction of H is

D m

1

y cos 

cos  d .cos /

1

y cos 

d .cos /

: (1.30)

The details of the integration over the energy states may be found in most standard

texts on magnetism. For the purposes of this introductory exercise, a summary of

the results will be sufﬁcient:

D L.y/D cothy 

; (1.31)

where L .y/ is the Langevin function and y D mH= kT . For typical ﬁelds and

temperatures in the paramagnetic region, y  1. In this limit, L .v/  y=3 and the

volume susceptibility may be expressed from (1.8)as



par

4n Nm

4nm

L.y/ 

4nm

3kT

; (1.32)

where n is the volume density of magnetic moments, so that 4nm corresponds to

the magnetization 4M .

Reﬁnement to this theory was contributed by Brillouin, who introduced the

2J C 1s multiplicity to Langevin’s assumption (1). In this case, the decrease in

energy of (1.29) becomes

Dgm

J.J C 1/H Dgm

H; (1.33)

and the total moment per unit volume in the direction of H is

n Nm

ng m

J

; (1.34)

1.2 Induced Magnetism 13

where y D gm

H=kT and the sums are over the allowed M

values from CJ to

J . Through a combination of integration and series summation, (1.34)istrans-

formed to

n Nm

D ng m



2J C 1

coth



2J C 1



y 

coth



: (1.35)

To expose the inﬂuence of different J values on the maximum z-component of

ng m

J ,

it is convenientto make a further substitution of y D a=J , which modiﬁes

(1.35)to

n Nm

ng m

D B .a/ D

2J C 1

coth



2J C 1



a 

coth

; (1.36)

where B .a/ is the celebrated Brillouin function. Since the assumption that y  1

also applies to a in the paramagnetic limit, (1.36) reduces to

B .a/ 

J C 1

a 



J C 1



C 2J C 1

30J



: (1.37)

If the cubic term is ignored in this approximation, we can substitute m D gm

into (1.32) and then apply (1.37) to express the susceptibility as



par

4ngm

B .a/ Š

4ng

J.J C 1/m

3kT

: (1.38)

Equation (1.38) is also a phenomenological explanation for the empirical Curie law



par

D C=T, with the Curie constant

C D ng

J.JC 1/ m

=3k: (1.39)

Because m

D gm

J.JC 1/ from (1.26), (1.32)and(1.38) indicate that the

Langevin and Brillouin functions are equivalent in the linear paramagnetic region

at low H or high T . Where the two theories differ is in the saturation values of

ng m

J z

, which are proportional to J in the Brillouin function instead of

J.J C 1/

because of the spatial quantization of the magnetic moment. Only as J !1do the

two curves merge, as seen in Fig. 1.5. The accuracy of the Brillouin function was

veriﬁed experimentally under saturation conditions as shown in Fig. 1.6 for ions of

different J values [3].

Where h is absorbed into m

in magnetic analyses, the practice of replacing M

with J

as the

z-component of J , or simply using J as the angular momentum counting parameter has become

accepted. This is particularly true in the widespread application of the Ising approximation to

the Heisenberg model of magnetic exchange. However, where angular momentum is not directly

involved in magnetic concerns, for example, electric-dipole transitions discussed in Chap. 7, h must

not be forgotten.

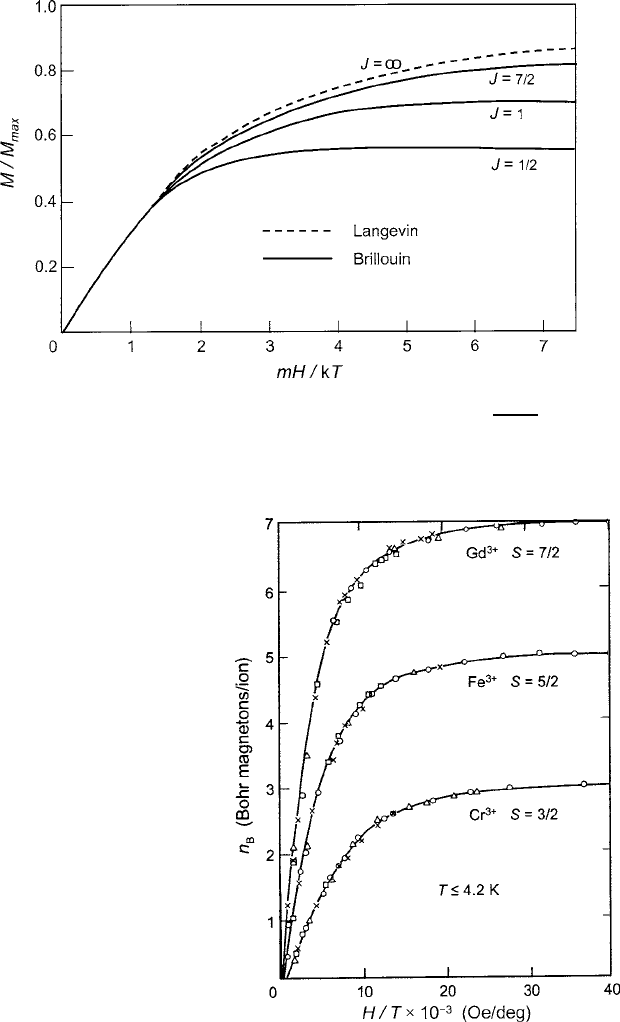
14 1 Introductory Magnetism

Fig. 1.5 Standard graphs of the Langevin and Brillouin models as a function mH=kT for J D

1=2,1,7/2,and1. Note that M remainslessthanM

max

(proportional to J

J C 1) because of

the quantum correction, and that the two models merge only as J !1

Fig. 1.6 Paramagnetic

saturation in potassium

chromium alum

J D 3=2

ferric ammonium alum

J D 5=2

, and gadolinium

sulphate octahydrate

J D 7=2

. Data from

W.E. Henry [3]

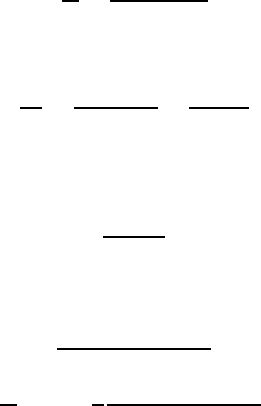
1.3 Spontaneous Magnetism 15

1.3 Spontaneous Magnetism

The interactions of magnetic moments in the preceding discussion have been limited

to mutual coupling through dipolar ﬁelds and with external ﬁelds. The most in-

tense manifestation of magnetic phenomena in solids occurs when the moments are

brought close together where the short-range forces of chemical bonding inﬂuence

strong parallel or antiparallel alignments. What distinguishes these phenomena from

diamagnetism and paramagnetism is that the materials may remain magnetized in

the absence of a magnetic ﬁeld. For that reason, magnetism associated with the

chemical bonding is referred to as spontaneous.

1.3.1 Classical Ferromagnetism and Antiferromagnetism

Although the Langevin and Brillouin functions provide a phenomenological basis

for the empirical Curie law, the behavior of the susceptibility at the onset of spon-

taneous magnetic ordering is not accounted for. To introduce these effects, Weiss

added a term to H that represents the collective inﬂuence of the neighboring mag-

netic moments. This modiﬁcation deﬁned an effective Weiss “molecular” ﬁeld

D H C N

M; (1.40)

where N

is the resultant Weiss molecular-ﬁeld coefﬁcient, which is dimensionless

when the magnetic moment is expressed as a volume density, that is, as magnetiza-

tion M . By manipulation of (1.32)and(1.38), the magnetic susceptibility relation

that includes the exchange ﬁeld H

becomes



H C N

; (1.41)

which can be converted to



T  CN

T  

; (1.42)

where 

is the Curie temperature parameter for ferromagnetism. An analogous

relation describes the antiferromagnetic case, according to



T C 

: (1.43)

From (1.39), the paramagnetic Curie and N´eel parameters are given by



D CN

J.JC 1/ m

;



D

J.JC 1/ m

: (1.44)

16 1 Introductory Magnetism

Fig. 1.7 Schematic of

inverse susceptibility vs.

temperature comparing the

Curie–Weiss law for

paramagnetism and two

spontaneous cases,

ferromagnetism and

antiferromagnetism

In the antiferromagnetic case, N

represents the resultant coefﬁcient of the oppos-

ing sublattices, with the factor 2 in the denominator because the population of like

spins in each sublattice is n=2. It must be noted that 

and 

are smaller in mag-

nitude than the actual T

and T

threshold temperatures for long-range magnetic

order. In most cases, T

 

, but the relation between T

and 

is more complex

because of the competing inter- and intrasublattice molecular ﬁelds. Only where the

intersublattice molecular ﬁeld is dominant can the aforementioned relation for 

be equated to T

. This subject is examined further in Chap.3.

For N

>0, parallel alignment is the result; for N

<0, the alignment is

antiparallel. By plotting measurement data of 1= as a function of T as illustrated

in Fig. 1.7,valuesofC and 

or 

may be determined from the slope and intercept

of the straight-line graph formed from the linear function. From these results values

of N

can be deduced.

The ability to obtain basic information about the strength of spontaneous mag-

netism from these plots represented an important milestone in the investigation of

magnetism. With the introduction of the molecular or mean ﬁeld concept, the varia-

tion in magnetization as a function of temperature in the ferromagnetic state can be

calculated with good accuracy.

1.3.2 Solutions of the Brillouin–Weiss Equation

The variation of magnetization with temperature and magnetic ﬁeld in the ferromag-

netic state may be computed by substituting the relation for the effective magnetic

ﬁeld of (1.40) into the previously deﬁned expressions for E

, y,anda. Accordingly,

eff

ŒH C N

M.T/

ŒH C N

M.0/B .a

eff

/ : (1.45)

1.3 Spontaneous Magnetism 17

Because a

eff

is now a function of B .a

eff

/,(1.36) can no longer be solved in closed

form. The most expeditious way to solve for B as a function of T and H is through

the use of a numerical iteration code that is managed easily by a digital computer,

which is reviewed in Sects.3.2 and 4.1. In many textbooks [4, 5], however, graph-

ical solutions are indicated, and there is merit in reviewing the results of these

procedures. To investigate spontaneous magnetization, we set H D 0 and rearrange

(1.45) to obtain a second relation between M.T/=M.0/and a

eff

,sothat

M.T /

M.0/

eff

(1.46)

and from (1.36)

M.T/

M.0/

D B .a

eff

/; (1.47)

where T is emphasized as the principal independent variable, and M.0/D ngm

J .

Solutions for M.T/=M.0/as a function of a

eff

are found by plotting (1.46)and

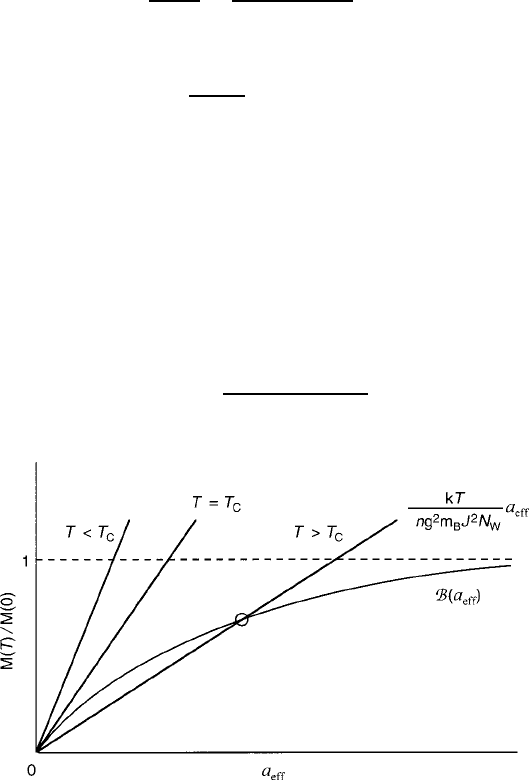
(1.47) as shown in the standard graph of Fig. 1.8 and by noting the nonzero inter-

section of the linear curve with the Brillouin function curve. The Curie temperature,

which is the highest temperature for which spontaneous magnetic order can exist,

is that obtained from the slope of the linear curve that matches the asymptote of the

B vs . a

eff

curve at the origin. As contained in the linear term in (1.37), the slope of

B at the limit of a

eff

 1 is given by Œ.J C 1/ =3J  a

eff

, which leads directly to the

limiting value of temperature for spontaneous magnetism

D 

J.J C 1/

: (1.48)

Fig. 1.8 Graphical solution for the Curie temperature, as described in text. Spontaneous mag-

netism breaks down at the temperature where the linear curve becomes tangential at the origin of

the Brillouin curve

18 1 Introductory Magnetism

Fig. 1.9 Universal Brillouin–Weiss curves for J D 1=2,1,and1, with H

 H

From (1.46)and(1.48) a universal relation can be constructed according to

M.T/

M.0/



J C 1





eff

: (1.49)

Universal curves of the Brillouin–Weiss theory are shown in Fig. 1.9,whereB is

presented for different values of J . The curve for j !1is the Langevin limit

where

J.JC 1/ ! J .

Another useful relation can be obtained by combining (1.37)and(1.49)to

eliminate a

eff



M.T/

M.0/



.J C 1/

C .J C 1/



1 





.J C 1/

C .J C 1/



1 



for

! 1: (1.50)

This relation indicates that M (T) is a continuous function of temperature up to the

Curie temperature. It also reveals that the M.T/=M.0/follows a .1  T=T

1=2

near the Curie temperature, and that its slope tends to inﬁnity at T D T

.The

exponent 1/2 was subsequently deﬁned by the parameter ˇ, sometimes called the

scaling constant, which usually assumes values lower than 1/2 in other models of

the approach to the Curie temperature.