Dionne G.F. Magnetic Oxides

Подождите немного. Документ загружается.

50 2 Magnetic Ions in Oxides

half of the shell begins to ﬁll, the sixth electron must now share an orbit with its spin

antiparallel to the net spin of the lower half in order to satisfy the Pauli principle.

The natural consequence is an abrupt increase in energy for d

that is the direct

result of the e

correlated repulsion. From d

to d

, the process is repeated

with a positive energy increment until the d shell is ﬁlled and the net spin returns

to S D 0, at which point the d states can be considered part of the closed-shell

ion core. The effect on energy from the ﬁlling of the d-orbital shell obeying Hund’s

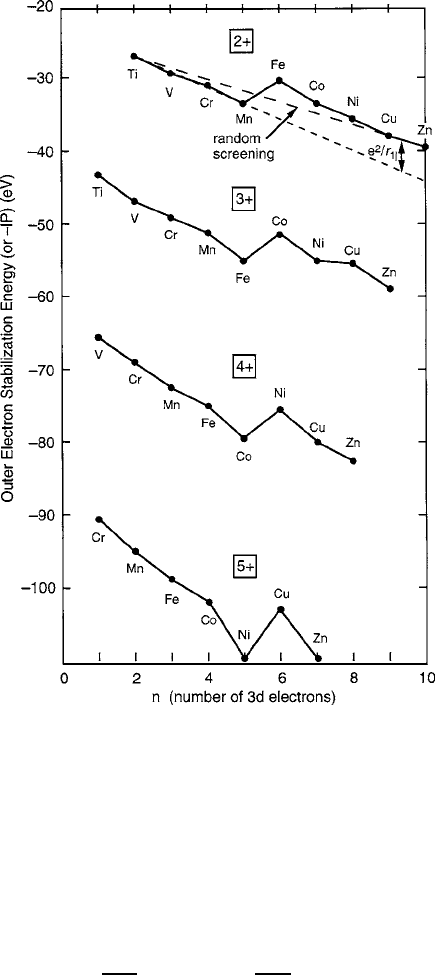
rule can be seen in the ionization potentials (plotted negative relative to free space)

in Fig. 2.8 as a function of n for different ionic valences across the transition series.

Note that the departures from the baseline for random dispersal are consistent with

the concept that the internal alignment (intraexchange) energy U

is proportional to

the net spin value of the ion, and that the maximum destabilization between up and

down spins is on the order of 2–3 eV.

More important for the immediate discussion are the combined values of L,

which can be calculated by straightforward additions of m

in each column. The

resultant designations for the ground terms of each free ion

2SC1

indicate that

only three orbital degeneracies occur in the d -electron transition series: S, D, and

F, but not P. Since the S represents an L D 0 state, d

automatically becomes a

spin-only magnetic entity, which greatly simpliﬁes analysis of magnetic properties,

at least to ﬁrst-order approximation.

When a positive magnetic ion is subjected to the electric ﬁeld of the negative an-

ion charges, the lobes of the electron orbital wavefunctions react to repulsive forces

that either stabilize or destabilize the different orbitals depending on their relative

proximity to the orbital lobes of the ligands, for example, 2p

x;y;z

orbital functions

of oxygen. In the broadest of contexts, the orbital angular momentum is captured

by the crystal ﬁeld, and in the process it is decoupled from the magnetic moments

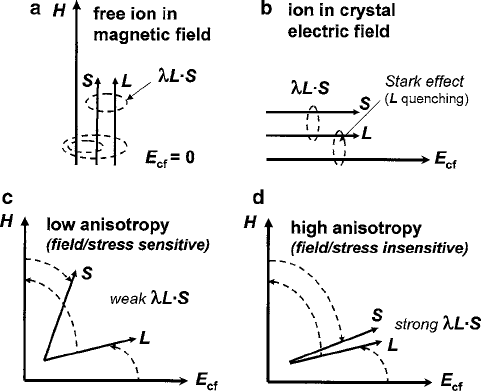
of the electron spins. A sketch of this quenching effect and its relation to spin–orbit

coupling is presented in Fig.2.9 for a uniaxial crystal ﬁeld that separates the L and

S vectors when it is not collinear with a magnetic ﬁeld vector H . Crystal-ﬁeld the-

ory is applied through quantum mechanical methods to determine the energy level

structures of the resultant orbital states and their associated eigenfunctions.

2.3.2 Crystal Field Hamiltonian

Before the effects of the crystalline environment on the cation energy states are

considered, the Hamiltonian of the free or unperturbed ion must be reviewed. A

more complete discussion can be found in other texts [3–6] that have emanated from

the treatise by Condon and Shortley [7]. If the terms involving neighboring nuclear

charges are omitted, the Hamiltonian for a free ion of angular and spin momentum

quantum numbers L and S

H D ŒH

Coul

C H

Hund

 C H

; (2.1)

2.3 Crystal Electric Fields 51

Fig. 2.8 Electronic energies of d-shell ions plotted as reverse ionization potentials. Note stabi-

lizing effects of Hund’s rule spin polarization and the destabilization by U

D e

needed to

establish Pauli spin pairing, as the upper half of shell ﬁlls. The electrons of the half-ﬁlled shell d





are the most stable, and the d

conﬁguration is the least stable, which explains why Fe

ions frequently act as electron “donors” in charge transfer phenomena in mixed-valence situations

with Fe

ions. Conversely, the unﬁlled upper half shell can be the source of holes, as in the case

of d

(e.g., Mn

), which then act as “acceptors.” Data are from C.E. Moore, NSRDS-NBS 34,

Ofﬁce of Standard Reference Data, National Bureau of Standards, Washington, DC

where the bracketed terms are the free-ion energies comprising

Coul

D

„



10

1



;

the basic relation containing the Coulomb attractive energy between the Z elec-

trons and the nuclear charge separated by r

,andH

Hund

i>j

, the energy of

52 2 Magnetic Ions in Oxides

Fig. 2.9 Orbital angular momentum and spin–orbit coupling in a uniaxial crystal ﬁeld: (a)mag-

netic ﬁeld H acting on a free magnetic ion aligns the orbital L and spin S angular momentum

vectors already made collinear through spin–orbit coupling œ LS ,(b) independent of H , lattice

crystal-ﬁeld E

(presented as orthogonal to H axis) couples with L, creating a Stark effect that

partially “quenches” the orbital magnetic moment and causes an elastic distortion of the ion site,

a magnetostrictive effect that creates high magnetic sensitivity to both ﬁeld and external stress if

spin–orbit coupling is weak. This is the case of “soft” magnetization, and (d) similar to (c) but with

spin–orbit interaction strong enough to produce substantial magnetocrystalline anisotropy that re-

duces magnetic sensitivity and creates a condition for “hard” magnetization. The Stark distortion

effect can also be the result of spontaneous local orbit–lattice (Jahn–Teller) stabilizations in which

spin–orbit coupling mediates interactions between orbit–lattice stabilizations and a magnetically

polarized spin system

mutual repulsion between the Z electrons orbiting the same nucleus and separated

by r

. The latter quantity is a concern for ions with multiple unpaired electrons in

an unﬁlled shell, particularly in the presence of strong crystal ﬁelds. In combination

with the crystal ﬁeld, the H

Hund

operator is responsible for the distribution of elec-

trons among the various orbital states of the unﬁlled shell and therefore the ordering

and separation of the orbital energy terms, which have been computed and thor-

oughly documented in the literature of atomic physics [7]. The eigenfunctions of this

free-ion Hamiltonian are the familiar solutions of the Schr¨odinger equation in the

form of exponentially decaying radially symmetric functions R.r/ combined with

spherical harmonics Y

that shape the various wavefunction lobes, according to



D R.r/Y

: (2.2)

The R.r/function is in part a decaying exponential that is common to all orbitals

within a main Bohr “n” shell. For a given transition series, it is treated as a scale

2.3 Crystal Electric Fields 53

constant. The various terms formed from the spherical harmonics tend to be ordered

energetically according to Hund’s

2SC1

L rule, which states that the lower energies

favor ﬁrst the highest multiplicities 2S C1 and then the highest L within each 2S C1

group. For the 3d

series, the 3d

case with L D 2 and S D 1=2,

D is the only

orbital term because the inﬂuence of the H

Hund

mutual repulsion energy is moot.

The solutions for the multiple electron cases, which are sorted out by the inﬂu-

ence of H

Hund

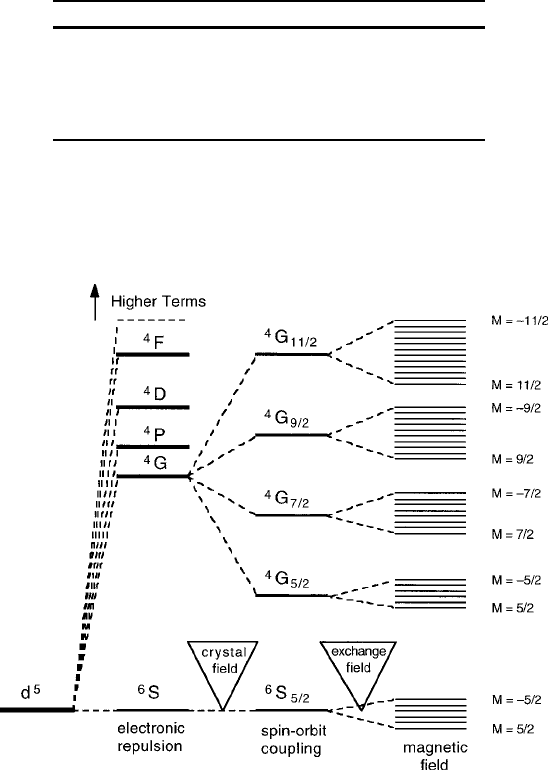
, are listed in Table 2.4. An example of the important ﬁve-electron

case 3d

corresponding to Fe

isshowninFig.2.10, with the

S ground term and

Table 2.4 3d

(iron-group) free-ion energy terms (lowest 5)



















–

a 4

–

There are two values for this term

For this case in particular the order of the term energies does

not follow the approximation of Hund’s rule. This is

characteristic of the higher energy terms in conﬁgurations with

greater numbers of d electrons

Fig. 2.10 Generic model of energy-level structure of ﬁve-d electron





conﬁguration, typical

of the Fe

3C6

S-state ion

54 2 Magnetic Ions in Oxides

the ﬁrst excited term

G with its subsequent multiplet splittings and eventual Zee-

man splittings in a magnetic ﬁeld. A physical picture of the

G state would have the

D2 state electron shown in the occupancy diagram of Fig. 2.3 reversing its

spin sense to form a pair in the m

D 2 orbit and provide a resultant L D 4 with

an S D 3=2. This conﬁguration will be shown in Chap. 5 to provide the basis for

magnetic anisotropy of iron in cubic crystal ﬁelds. The spin–orbit coupling energy

is the third term in (2.1); H



.r/ l

 s

.10

1

for the iron group and

1

for the rare-earth group) is the perturbation that produces the multiplet

structure observed in atomic spectra. Where the coupling functions 

.r/ are sufﬁ-

ciently invariant among the states, they are usually combined into a semiempirical

constant 

When the ion is situated in a crystal lattice, a crystal ﬁeld term H

must be added

to (2.1) to account for the interactions between the electron charges and the electric

ﬁeld of the crystal lattice environment:

H D ŒH

Coul

C H

Hund

 C H

C H

: (2.3)

In the simplest approximation, the source of H

is represented as point charges

ﬁxed at the locations of the particular ligands (anions) surrounding the cation. The

purpose is to simulate a Stark effect coupling between the orbital angular momen-

tum L and the crystal ﬁeld that competes with the spin–orbit coupling between S

and L as depicted in Fig. 2.9. The immediate effects are to make S as the principal

source of the magnetic moment and remove J as a “good” quantum number. This

action by the crystal ﬁeld is called “quenching” of the orbital magnetism and results

in g  2 when it is dominant.

2.3.3 Hierarchy of Perturbations

As suggested by the order of terms in (2.3), H

is usually smaller than the lattice-

related perturbation terms. At this point it becomes both convenient and instructive

to deﬁne three crystal ﬁeld regimes, deﬁned loosely as weak and strong for the d

series, and the shielded case of the 4f

rare-earths, according to

Hund

> H

.3d

series/;

 H

Hund

.4d

and 5d

series/; (2.4)

< H

.4f

series/:

The ﬁrst of these is the one of principal interest because it applies to the most

commonly encountered iron group 3d

series. In this “weak ﬁeld” case, the crys-

tal ﬁeld is smaller than the energy term separations due the H

Hund

repulsive energy

of (2.1) listed in Table 2.4. Consequently, the starting free-ion terms in a perturba-

tion calculation are not mixed, only their degeneracies are split into ﬁne structures

2.3 Crystal Electric Fields 55

by the crystal ﬁelds. Moreover, only the ground terms need to be considered for

interpreting most magnetic effects. These operations and their implications on the

magnetic properties will be the main topic of this text.

The “strong ﬁeld” second case is also important, perhaps more for the high-

energy transitions to be examined in a later discussion of magneto-optical proper-

ties. It is analytically more challenging than the “weak ﬁeld” case because the H

magnitudes are equal or greater than the free-ion term splittings set by H

Hund

and

are therefore strong enough to mix the starting orbital terms prior to the removal of

their degeneracies. As a result, the various possible electron distributions among the

individual d orbital states, that is, the excited states, must be included as separate

energy levels prior to application of the symmetry constraints imposed by the H

operator. The strong ﬁeld situation is sometimes referred to as the covalent limit

because the strong H

potential energy is produced by the overlap of the cation and

anion orbital lobes. It is more common among the 4d

and 5d

transition series ions

with larger ionic radii, but can also apply in the 3d

series when the anion complex

provides a locally stronger crystal ﬁeld than that of the standard O

2

coordinations.

In certain cases the crystal-ﬁeld splitting can be large enough to cause a breakdown

in Hund’s maximum S rule by producing what is called a “low-spin” state that then

leads to a change in the orbital ground term.

The third is the rare-earth 4f

case, in which the Stark effect of the crystal ﬁeld

is not great enough to decouple L from S because of the shielding by the ﬁlled

and 5p

shells. Here, œL  S remains a constant of the motion and the H

operation creates the various multiplet terms now identiﬁed by

2SC1

,whereL

represents the orbital angular momentum of the orbital term designated by S, P, D,

F, G, etc, with respective values of L being 0, 1, 2, 3, 4. For the rare earths, the

total angular momentum J and its speciﬁc g value as deﬁned by (1.29), rather than

simply S with its ﬁxed g D 2, determine the individual ion contributions to the

magnetic properties.

2.3.4 Weak-Field Solutions

The subject of crystal ﬁeld theory has been presented in many excellent texts [3–5].

Historically, the seminal work was carried out by Kramers [8], Van Vleck [9], and

Schlapp and Penney [10], who treated the combined effects of the various lattice

charges at a given cation site as the result of repulsive electrostatic ﬁelds from neg-

ative point charges that represent the effects of the anions or ligands. Because the

potential V

cryst

at the cation site from the assembly of neighboring charges satisﬁes

Laplace’s equation r

D 0, H

.DeV

/ may be expressed as an expansion of

generalized Legendre polynomials, which take the same familiar form of spherical

harmonics comprising (2.2). The problem of applying quantum perturbation theory

to determine the electronic states of the cation in a particular crystal ﬁeld is then

reduced to the solving of a secular equation,

56 2 Magnetic Ions in Oxides

cfij

 E

D 0; (2.5)

where H

cfij

, i and j are integers that run from 1 to k. E

are the k

eigenvalue solutions of the matrix, each representing new energy states depending

on the extent of the degeneracy removal. In this case it is the orbital angular mo-

mentum degeneracies of the spherical harmonic parts of the free ion wavefunctions

of (2.2) that determine the order of the splittings.

To illustrate the method, the example of a singled electron will be reviewed. The

spherical harmonic functions (also expressed in the d

abbreviations) for the

term are given in Cartesian coordinates by

2

D d

2

4

.x  iy/

;

1

D d

1

4

z .x  iy/

;

D d

4

 r

; (2.6)

D d

D

4

z .x C iy/

;

D d

4

.x C iy/

For an octahedral .O

/ site, the crystal ﬁeld potential energy is given by [11]

oct

D D



C y

C z





C higher order terms: (2.7)

Expressed in spherical harmonics, (2.7) becomes

oct









4













6





(2.8)

where D

D .35=4/ Ze

and D

D .21=2/ Ze

and a is the cation to anion

distance. The additional spherical harmonics are expressed as [12]

4

 r

;

4

35z

 30z

C 3r

;

C Y

4

4

 6x

C y

; (2.9)

2.3 Crystal Electric Fields 57

4

256

231z

 315z

C 105z

 5r

;

C Y

6

231

4

512

 15x

C 15x

 y

For the tetrahedral .O

/ and cubic .O

/ coordinations only the Y

terms of (2.8)

enter the calculation. Their crystal ﬁeld energies scale according to

tet

D.4=9/ V

oct

;

cub

D.8=9/ V

oct

: (2.10)

If the radial part of (2.2) is folded into the scale factor of the matrix elements within

the n D 3 shell, we may work with only the Y

functions of (2.6)tosetupa5  5

matrix based on (2.5). Following this step, diagonalization with the aid of rotational

symmetry considerations (group theory) or by solution of the secular equation will

separate the 5  5 matrix into a 2  2 and a 3  3 matrix, according to

C d

2

D d

; (2.11)



D d

1

;

 d

2

The degree of crystal-ﬁeld quenching of the orbital angular momentum about the

[001] axis may be checked by the expectation values of the l

operator from the

appropriate inner products to show that, in addition to d

,thee

and t

states have

D 0, while the remaining two t

states retain m

D˙1. If the function set

of (2.11) are formed into the set of linear combinations in real form sketched in

Fig. 2.11, they are expressed as

(

y

C d

2

/ D



C Y

2





 y



D d

D Y



 r



)

;

 d

2

/ D



 Y

2



3xy

D

 d

1

/ D



 Y

1



3xz

D

C d

1

/ D



C Y

1



3yz

;

; (2.12)

where the radial factor R.r/ and other common factors have been dropped for

convenience. The designations e

and t

are from group theory conventions for

individual electron orbitals. (A more general nomenclature for these states that is

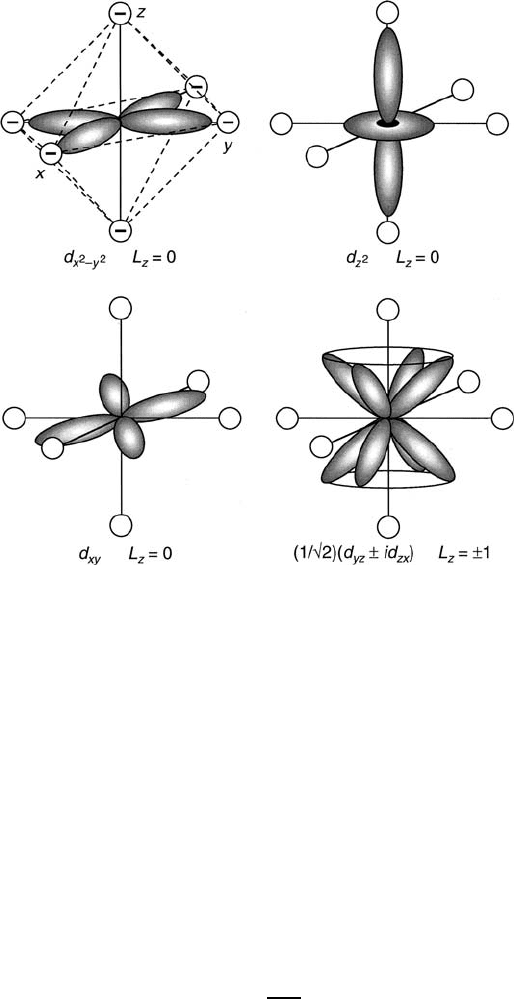
58 2 Magnetic Ions in Oxides

Fig. 2.11 Eigenfunctions lobes of the d -electron shell with orbital angular momentum quenched

by a crystal ﬁeld of tetragonal

symmetry. Only the d

, d

states remain degenerate with

nonzero L

D˙1

used where multiple electrons are involved is A

, A

for singlets (also B

, B

lower symmetry reﬁnements), E

for doublets, and T

, T

for triplets). With this

set of wavefunctions, the matrix is diagonal, so that the eigenvalues of (2.5) become







y

D "

C "

D "

C "



(2.13a)

and





D "

C "

D "

C "

D "

C "

;

; (2.13b)

where V

D Y



C Y

4



: (2.14)

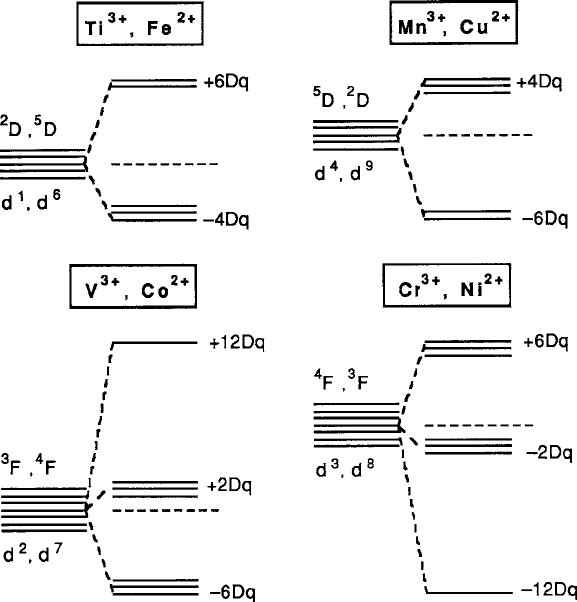
2.3 Crystal Electric Fields 59

Fig. 2.12 Multiple electron crystal-ﬁeld energy levels for D and F terms indicating correspon-

dence between members of the lower and upper halves of the 3d

transition series

which is derived from the octahedral potential energy of (2.8), without the normal-

izing factors. Equation (2.13) indicates that the ﬁvefold degeneracy of the

Dor

term .L D 2/ is split into a doublet and triplet. If the free ion ground term is

For

F .L D 3/, there are seven orbital states that are split into a singlet and two triplets

as sketched in the four basic octahedral crystal-ﬁeld diagrams of Fig. 2.12.Theen-

ergy ordering of the levels, that is, upright or inverted, is a matter determined by the

spin occupancy and Hund’s rule and is examined in Sect. 2.4. The correspondence

between d

and d

10n

conﬁgurations can be reasoned by recognizing that d

fea-

tures electrons and d

10n

holes, which become distinguishable under the inﬂuence

of the ligand charges. For this reason, level inversion occurs between the d

and

10n

ions, that is, equal numbers of unpaired electron spins vs. “hole” spins. A

further convention is to label the overall splitting equal to 10Dq,whereDq > 0.

Then

 "

D 10Dq: (2.15)