Dionne G.F. Magnetic Oxides

Подождите немного. Документ загружается.

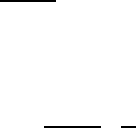
1.3 Spontaneous Magnetism 19

At temperatures near 0 K, a relation that has its origins in spin-wave theory has

proven to be the more effective at ﬁtting data than the Brillouin function. It is com-

monly referred to as the Bloch T

3=2

law and is given by

M.T/

M.0/

D 1  AT

3=2

; (1.51)

where the exchange constant J enters the relation through the parameter

A D

0:1174





3=2

and f D 1, 2, or 4 for the simple, body-centered, or face-centered cubic lattice,

respectively.

The values of B as a function of T can also be computed [6] by means of a

convergent iterative procedure that is described in Chap. 4 in relation to multiple

sublattice ferrites. The importance of the Brillouin function will revisited in the

discussions of antiferromagnetism. In Chap. 7, an external ﬁeld H is included as

an active variable in combination with the molecular ﬁeld to illustrate the origin of

magnetoresistance properties of magnetic oxides.

1.3.3 Quantum Origins of the Molecular Field

The origin of the Weiss molecular ﬁeld was ﬁrst proposed by Heisenberg [7], who

postulated that spontaneous spin alignments are determined by short-range interac-

tions between adjacent spins that are made possible by the coupling of orbital wave

functions as part of the chemical bonding. The effect is electrostatic and arises from

electron exchange between bonding atoms. In a quantum mechanical format, the

Heisenberg exchange energy is expressed as a Hamiltonian function with adjacent

spins at sites i and j related by

D2

i>j

 S

; (1.52)

where J

is the exchange constant. Phenomenologically, the sign of J

determines

the type of spin alignment; intuitively, it is seen that J

> 0 will cause ferromag-

netism and J

< 0 will create antiferromagnetism depending on the cosine of the

angle between S

and S

The orbital interactions the determine J

are analyzed through the use of the

one-electron Hartree–Fock approximation to the wave functions of a many elec-

tron system, with modiﬁcations required to account for the indistinguishability of

20 1 Introductory Magnetism

fermions and satisfy the Pauli exclusion principle [8]. An example that can illustrate

the quantum mechanical origin of the effect is the case of two one-electron atoms

a and b with corresponding electrons labeled (1) and (2). This is the hydrogen

molecule (H

) employing the valence-bond approach of Heitler and London [9].

The Hamiltonian (here representing a local Madelung energy) for this pair before

taking into account the electron–electron repulsion is therefore

D

„







; (1.53)

where Z

and Z

are the respective nuclear charges. There are two possible solutions

to this equation, '

D '

.1/ '

(2) where the two electrons remain on their “home”

atoms, and '

D '

.2/ '

(1) where the electrons are exchanged between the two

atoms.

To this point in the analysis, the electrons have been treated as “distinguishable.”

However, orthogonality requires that their eigenfunctions satisfy the relation

; (1.54)

which means that two solutions exist:

D˙'

: (1.55)

Because neither of the basic wavefunctions '

nor '

can fulﬁll the indistinguisha-

bility requirement of (1.55), the usual linear combinations are constructed,

sym

C '

anti

 '

/: (1.56)

To satisfy the indistinguishability, wavefunctions must always be antisymmetric,

meaning that exchange of two fermions must always involve a sign reversal [8].

However, only '

anti

meets this criterion. To render both eigenfunctions antisymmet-

ric, the orbital functions must be completed by attaching the spin matrix functions



sym

(for parallel spins) and 

anti

(for antiparallel spins) to create the ﬁnal set

D '

anti



sym

;

D '

sym



anti

: (1.57)

For a two-electron molecule, the total spin for 

sym

is S D 1 from parallel spin

vectors, thereby forming a spin angular momentum triplet (S

D 1; 0; and  1 in

units of „). Conversely, 

anti

is the singlet S D 0 from antiparallel spins.

1.3 Spontaneous Magnetism 21

Fig. 1.10 Basic diagram of

magnetic exchange

interaction identifying the

various linkage distances

among positively charged

nuclei a and b and their

bonding electrons 1 and 2

The problem can now be solved by considering a perturbed Hamiltonian in the

form of H D H

C H

and by calculating the eigenvalues of the two states for the

various electrostatic interactions among the nuclei and electrons, according to











;

repulsion attraction (1.58)

as depicted in Fig. 1.10. Computing the expectation values of the integrals

;

; and

produces the energy eigen-

values given in a form that exposes the spin exchange operator as determined by the

procedure of second quantization using Fermi operators [10,11],

E D K  J



C 2s

 s



; (1.59)

where

K D

.Coulomb integral/;

J D

.exchange integral/: (1.60)

To calculate the exact quantum mechanical values of the s

 s

scalar product (in

units of „

), the standard relation for the angular momentum vector addition s

D S can be used:

 s

D S.SC 1/  s

C 1/  s

C 1/ : (1.61)

For the parallel and antiparallel values of S D 1 and 0, respectively, and the values

of s

D s

D 1=2,(1.59) reduces to

E D K  J for S D 1.ferromagnetism/;

E D K C J for S D 0.antiferromagnetism/: (1.62)

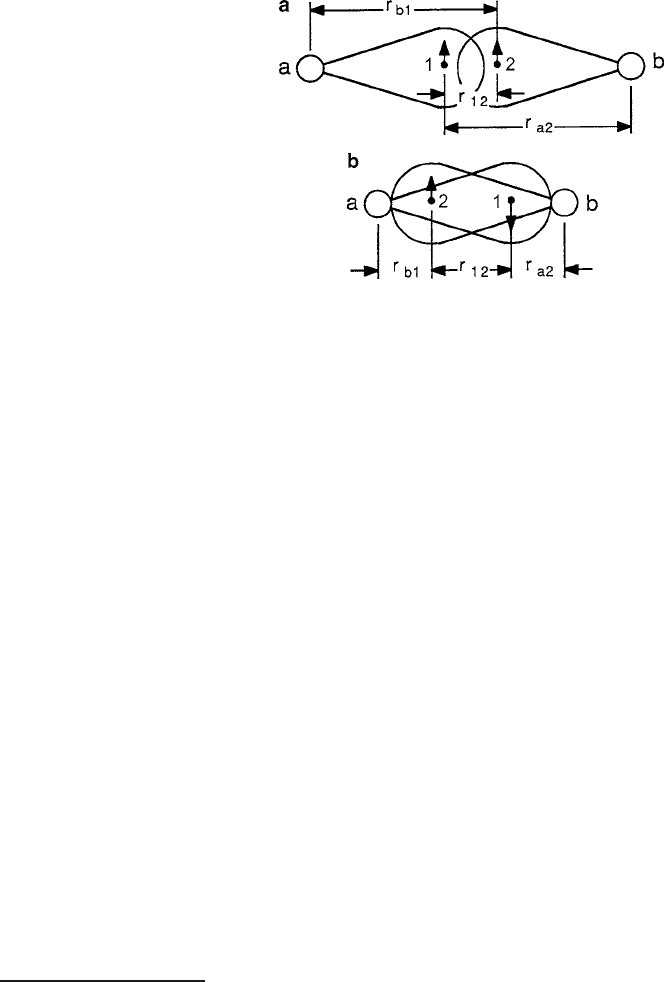
22 1 Introductory Magnetism

Fig. 1.11 Orbital interaction

diagram contrasting the

competing roles of mutual

electron repulsion and

electron-nuclear attraction as

nuclear separation decreases:

(a) ferromagnetism in an

antibonding state, and (b)

antiferromagnetism in a

bonding state. Note the

reversed locations of

electrons 1 and 2 relative to

the two nuclei

The choice of ground state in (1.62) is therefore determined by the sign of J ,which

follows the same rules that are stated below (1.52), that is, ferromagnetism for J>

0, antiferromagnetism for J<0.

Computation of J is not a trivial task, but some insight may be gained by in-

specting the relative sizes of the terms in (1.58) and comparing them with the

diagrams in Fig. 1.11. For overlapping orbital wave function lobes of the type shown

in Fig. 1.11a, the close proximity of the electron charge concentrations can make

the repulsive e

term dominant and render J>0, thereby establishing the

ferromagnetic

as the ground state. If the overlap is more extreme because of

a smaller r

distance, the situation of Fig. 1.11b would arise and the attractive

Z

and Z

terms could be large enough to make J<0and pro-

duce the antiferromagnetic

ground state.

Overlapping wavefunction lobes are characteristic of d and f electron shells.

Ferromagnetism is more likely to occur in the upper half of the iron group elements

because of their larger populations of unpaired and itinerant electrons. The graph

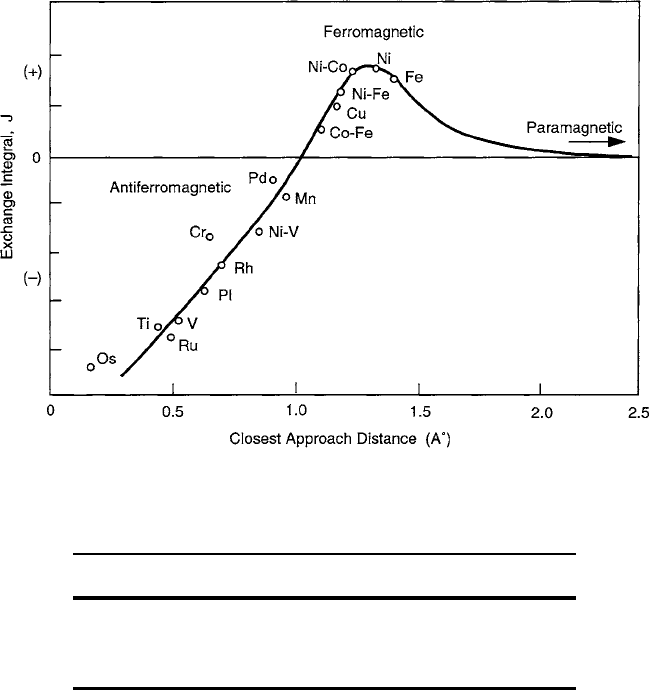
in Fig. 1.12 illustrates the qualitative support for this model, where J values were

estimated from Curie and N´eel temperature measurements. Positive J values occur

for larger r

distances in the familiar Fe, Co, and Ni of the 3d

transition group

and members of the 4f

rare-earth series.

An early phenomenological description of magnetic exchange was introduced by

Stoner [12]. Because of its success in interpreting magnetism in metals, it is known

as the theory of collective electron ferromagnetism. The result of this approach is

the band theory model that has helped to explain some features of the 3d

transition

series of elements. The theory predicts that ferromagnetic metals have moments that

are lower than anticipated based on the number of unpaired Bohr magnetons of the

Since the spins of an antiferromagnet are antisymmetric, it follows that the orbital functions must

be symmetric, and vice-versa for the ferromagnet. The former case is referred to as a “bonding”

state because of the orbital wavefunction overlaps, which is why most ionic compounds are in-

trinsically antiferromagnetic. The antibonding state then becomes a ferromagnet, as explained in

Chaps. 2 and 3.

1.3 Spontaneous Magnetism 23

Fig. 1.12 Chart of exchange constant data compiled as a function of the distance of closest ap-

proach of electron of neighboring atoms. Adapted from Lax and Button [14]

Table 1.3 Magnetic moments of ferromagnetic atoms

Transition

element

Free atom

conﬁguration

Solid state

distribution

Net 3d or 4f Bohr

magnetons

Fe 3d

7:4

0:6

C4:8  2:6 D 2:2

Co 3d

8:3

0:7

C5  3:3 D 1:7

Ni 3d

9:4

0:6

C5  4:4 D 0:6

Gd 4f

4f

7:1

0:9

7.10

free atom, as shown in Table 1.3. The reasons lie in the details of the overlapping

of 4s and 3d electronic bands in metals [13], as sketched in the density of states of

the split magnetic bands in Fig.1.13. Further support for the band concept is given

by the result for Gd

, which has seven unpaired electrons that occupy the shielded

4f inner shell and are thus exempted from the distractions of the 6s bonding states.

An effective approximation for insulator compounds is based on single-electron

molecular-orbital theory of covalent bonding. In contrast to the valence bond

method described earlier, molecular orbital theory focuses speciﬁcally on the

electron–nuclear interaction terms of (1.58) and ignores the mutual repulsion

, thereby favoring antiparallel spin alignment in the ground state. The

spin stabilization state that emerges is called indirect or superexchange because

the interactions between the positive magnetic ions (spin cations) occur through

the mediation of negative ligands (anions). It is particularly well suited for de-

scribing transition-metal insulating compounds where the basic exchange is

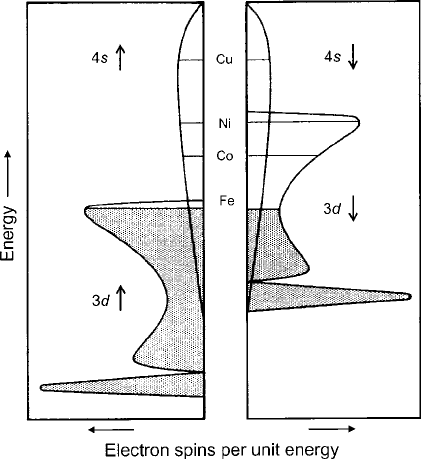
24 1 Introductory Magnetism

Fig. 1.13 Band model of

electron spin occupancy as a

function of energy for the

overlapping 3d and 4s bands

axis [12].Thebandsareﬁlled

to the levels indicated for iron

metal. The concept of

dividing the bands into

collective up and down spins

separated in energy by the

exchange stabilization [11]

resembles the application of

Hund’s rule in formulating

the ground-state spin

conﬁguration of

transition-metal ions, as

diagrammed in Figs. 2.3 and

2.19. Adapted from Lax and

Button [14]

antiferromagnetic. However, there are varying conditions of superexchange (in-

cluding charge transfer or itinerance) that apply to different cation–anion–cation

situations.

This subject is placed into a broader context in Chap. 3, where collective and

localized spontaneous magnetism are contrasted. In a normally antiferromagnetic

structure, ferromagnetism requires electron delocalization in the form of Fermi gas

conductivity or large-polaron charge transfer between magnetic cations in mixed-

valence compounds.

1.3.4 The Ising Approximation

The exact solutions of the total spin scalar product S

 S

eigenvalues require

the application of Fermi operators that lead to the mathematical and conceptual

complexities indicated by the stated result for the exchange energy E

taken from

(1.59). An effective simpliﬁcation called the Ising approximation has proven to be

accurate for most practical situations. If the exchange constant is the same for all

spin interactions, J

of (1.52) may be replaced by J and the scalar product can be

expanded and summed over the nearest neighbors S

of spin S

to give

D2J

i>j



C S



: (1.63)

1.4 Gyromagnetism 25

If the spin components are replaced by their time averages, and a total of z identical

nearest neighbors are included in the sum, (1.63) may be expressed as

D2zJ





: (1.64)

If the classical Larmor theory is used (see Sect. 1.5.1), the spin vectors will precess

about an effective molecular (or exchange) ﬁeld directed along the z-axis of quan-

tization. As a consequence, the time averages of the x and y spin components are

assumed to be zero, and

2zJ

: (1.65)

From this approximation a relation between the exchange integral J and the Weiss

molecular ﬁeld coefﬁcient N

may be derived. Since we consider only the z com-

ponent of the magnetization M



Dngm



and (1.65) becomes

2





: (1.66)

For H D 0, H

can also be expressed in terms of the Weiss molecular ﬁeld by

equating to E

from (1.33), according to

g

; (1.67)

where M

becomes S

and the applied ﬁeld H is replaced by the exchange ﬁeld

.From(1.66)and(1.67)

2zJ

; (1.68)

and we have for the Curie temperature from (1.48), after (1.68) is substituted,

2zJS .S C 1/

; (1.69)

with S replacing the total angular momentum .J / for our discussion of spin

exchange. Equations (1.68)and(1.69) are important in the models for thermomag-

netism and magnetoresistance.

1.4 Gyromagnetism

To this point in the discussion, there has been little mention of the spectroscopic

splitting factor g that was introduced as part of the quantum mechanical deﬁnition

of the magnetic moment. Before leaving this introductory chapter, it is appropriate

to explain the classical origins of the magnetic resonance phenomenon that is not

only an important topic for later parts of this text, but also provides a direct means

of measuring g.

26 1 Introductory Magnetism

1.4.1 Larmor Precession and Resonance

Magnetic resonance is based on a theorem that the motion of an electron under a

central force, for example, Coulomb attraction to a nucleus, and a magnetic ﬁeld H

in a ﬁxed coordinate system is identical to that of an electron under the same central

force with H D 0 in a coordinate system that is rotating about the H axis with

angular frequency

D H D

H; (1.70)

where !

is the Larmor precession frequency and g equals 1 for an orbiting electron

and 2 for an electron spin;



 D 1:76  10

rad=s=Oe



is usually referred to as the

gyromagnetic constant.

The derivation of this relation may be found in many stan-

dard textbooks [14,15]. For the diamagnetic case with g D 1, the sense of rotation

in the precession orbit is to establish a magnetic moment that is directed against H ,

thereby providing the basic mechanism for diamagnetism.

From the general case of a ﬁxed magnetic moment m in a ﬁeld H , the rotation

direction would be consistent with the moment and ﬁeld in parallel. The basic theory

of magnetic resonance may be derived from the equation of motion

.m  H /; (1.71)

where the vector m  H is normal to the plane containing m and H . Consequently,

the resulting torque causes the clockwise precession of m about H viewed along

the direction chosen as the z-axis of the magnetic ﬁeld. The solutions of (1.71)for

the individual components of m may be expressed as

D m sin  cos !

D m sin  sin !

t; (1.72)

D m cos  D constant:

where m forms a constant angle  with the z axis in establishing a cone of precession

at the Larmor frequency. Recalling the earlier discussion of the quantum mechanical

constraints on the values of the projection of m on the axis of quantization, we

express m

J z

D gm

since Planck’s constant „ is absorbed in the Bohr magneton.

Note also that from a quantum energy standpoint, the Zeeman splitting

„!

D gm

HJ

D gm

H forJ

D 1: (1.73)

The equivalence of (1.70)and(1.73) can be determined by inspection.

Where the frequency is designated by the symbols  or f expressed in cycles/s (Hz), an alterna-

tive constant 

D2:78GHz=kOe

is deﬁned. However, confusion can arise when the symbol !

is used for , usually in microwave engineering literature. In such instances, 

must be employed

with H . Note also that the negative sign of the electron charge e has been absorbed in the deﬁni-

tion of !

in (1.70), thereby allowing  to be treated as positive wherever frequency and ﬁeld or

magnetization are related.

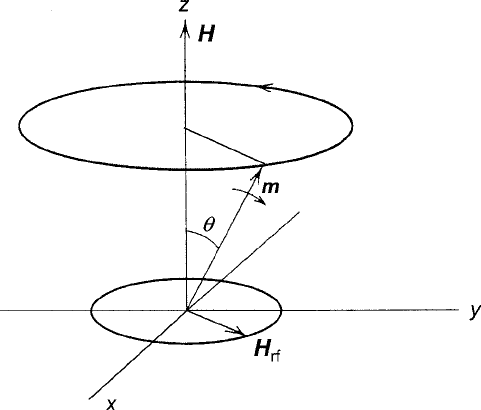
1.4 Gyromagnetism 27

Fig. 1.14 Standard classical diagram of magnetic resonance showing the precession of a magnetic

moment m about a ﬁeld H at the Larmor frequency. When a circularly polarized oscillating ﬁeld

matches the frequency and sense of the precession, m is subjected to a torque that rotates it

away from the H axis, thereby producing a complex susceptibility

Magnetic resonance occurs where an alternating (usually radio frequency) mag-

netic ﬁeld H

is applied in a direction perpendicular to H. Because a linearly

polarized signal can be decomposed into two counterrotating circularly polarized

signals, the physical situation resembles that depicted in Fig. 1.14, where only the

component that rotates in the direction of the precessing moment is capable of con-

tinuously inﬂuencing the angle of m relative to the z axis by creating a second torque

m H

normal to the m H direction. By setting the frequency of the alternating

ﬁeld at ! D !

, H

will synchronize with the precession and apply a constant

torque that will cause the cone half-angle  to oscillate from full alignment with H

. D 0/ to its opposite limit . D /. The rotation of m away from H represents

the absorption of energy. Where a quantum mechanical model can be applied, the

two extreme values of  represent two energy levels of a degeneracy that is split by

H (Zeeman effect). This view of magnetic resonance is explored in a discussion of

electron paramagnetic resonance in Chap. 6.

1.4.2 Phenomenological Relaxation Theory

An important feature of all resonating systems is the effect of damping. It

occurs most visibly in vibrating mechanical systems that reduce their amplitudes

exponentially because of air resistance or friction. The decay is a manifestation of

the loss of energy as the system relaxes back to equilibrium. For systems under

28 1 Introductory Magnetism

constant excitation, it is the energy that must be supplied to maintain the reso-

nance condition at a given intensity. In magnetic resonance, the relaxation arises

principally from two sources: (1) the transfer of magnetic energy imparted by the

alternating magnetic ﬁelds to the system of magnetic moments, commonly referred

to as the “spin system,” back to the environment, which is the lattice in the case of

solids and (2) the tendency of the precessing moments to lose phase coherence due

to perturbations of the external magnetic ﬁeld by local dipolar ﬁelds. The ﬁrst is loss

of signal energy directly to the lattice; the second is a loss of signal by decoherence

of the precessing spins. Eventually this energy will also be transformed into heat or

radiation.

In mathematical terms, following the approach developed by Bloch and

Bloembergen [16, 17], the relaxation of magnetization M .D˙m/ back toward

the z axis (longitudinal relaxation) following the removal of the H

ﬁeld is deter-

mined by the relaxation rate 

1

of its M

component

D

 M



D

 M



; (1.74)

where 

.D

/ is the spin–lattice relaxation time and M.DM

/ is the equilibrium

value of M

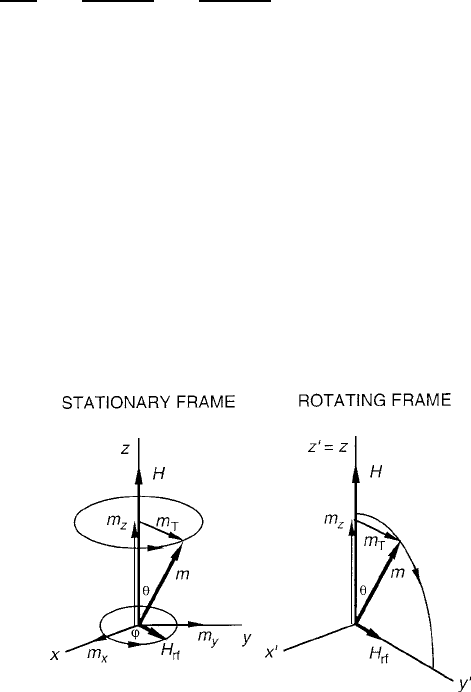
. In the stationary frame of reference of Fig. 1.15, the decay process of

the individual m vector can be visualized as following an inwardly precessing spiral.

Accordingly,

M  M

.t/ D ŒM  M

.t/ exp .t=

/: (1.75)

The second relaxation phenomenon of importance concerns the phase decoherence

of M

and M

among individual spin vectors as they precess about H (transverse

relaxation), which occurs in paramagnetic systems through dipole–dipole interac-

tions. In ferromagnetic systems, the decoherence represented by 

is seen in the

form of spin waves, which occur under special conditions. In this case the vector

components of the spins that are perpendicular to H ,thatis,M

and M

lose their

collective coherence at a rate deﬁned as 

1

, once the alternating drive ﬁeld is re-

Fig. 1.15 Two frames of

reference for magnetic

moment precession:

stationary and rotating at the

precession angular frequency