Dionne G.F. Magnetic Oxides

Подождите немного. Документ загружается.

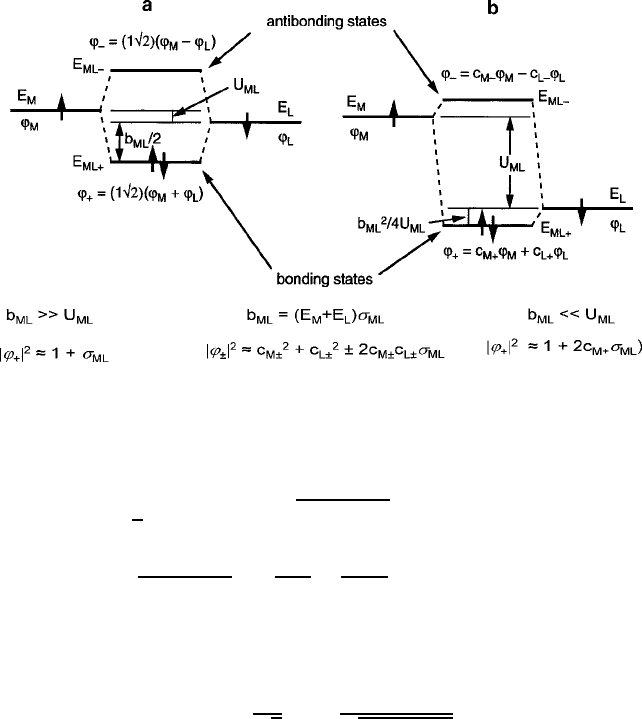
110 3 Magnetic Exchange in Oxides

Fig. 3.2 One-electron metal–ligand molecular orbital diagram illustrating the stabilization of an

electron spin pair and the formation of bonding and antibonding hybrid eigenstates for (a) b

,and(b) b

<< U





C E

/ ˙

C b





C E





for b

<< 1; (3.1)

where U

D E

–E

. Hybrid eigenfunctions are 

ML˙

D c

M˙



˙ c

L˙



where

M˙

D c

L



1 ˙

C b

1=2

: (3.2)

This approximation can be used as a building block to create an artiﬁcial M–L–M

molecule that represents the actual situations sketched in Fig. 3.3. By attaching a

second cation to the opposite lobe of the same ligand orbital function, we can con-

sider forming an illustrative model by pursuing a qualitative line of reasoning. To

reduce this three-body problem diagrammed in Fig. 3.4 to a manageable two-body

case, an effective overlap integral between M and M

must be deduced from the

bonding state of the M–L–M

molecule. Once this interaction parameter is deter-

mined, the M–M

coupling can be approximated in the manner of a simple diatomic

molecule.

From the MO diagram of Fig. 3.2, the unpaired 3d spins in the e

states are

localized to their respective nuclei in the '

ML

and '

L

antibonding states. The

smaller b

=4U

 10Dq is, the closer the levels will approach those of a “free”

ion. As long as the b

, b

¤ 0, however, a portion of the j'

and j'

den-

sities is hybridized with the j'

density in the lower energy bonding state. As a

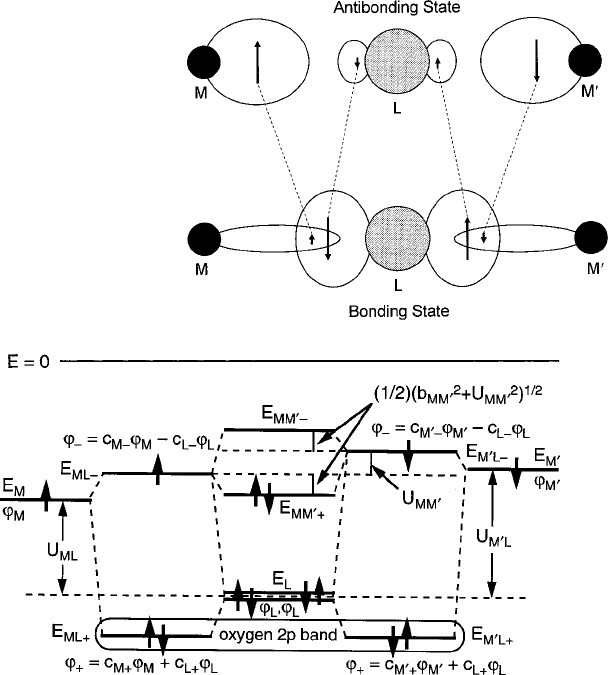
3.1 Interionic Magnetic Exchange 111

Fig. 3.3 One-dimensional

sketches of

metal–oxygen–metal

molecular orbital hybrid

states illustrating the

fractional spin distributions of

the respective 3d metal and

2p ligand wavefunctions

Fig. 3.4 One-electron metal–oxygen–metal molecular orbital diagram illustrating the formation

of the basic bonding and antibonding hybrid eigenstates that produce superexchange in magnetic

oxides. Figure reprinted from G.F. Dionne, J. Appl. Phys. 99, 08M913 (2006) with permission.



2006 by the American Institute of Physics

result, the two 3d spins are partially delocalized into antiferromagnetic states by an

effective overlap integral 

MLM

that is mediated through the ligand 2p orbital func-

tion containing its original paired spins. As depicted schematically in Figs. 3.1d, e,

excess densities in the regions between the cations and anion, i.e., (1 C 

), will

deﬁne the volume of bonding interaction, while depleted densities (1–

/ in the

corresponding antibonding states will restore the population total (see Appendix 3A

of Chap. 2). From this diagram, it is evident that the orbital stabilization occurs in

the bonding state, despite the fact that the 3d spins are mainly localized in the anti-

bonding state. The effective overlap integral 

MLM

can then be approximated from

the volumes of the two 3d wavefunctions represented in the bonding states j

MLC

and j

, i.e.,

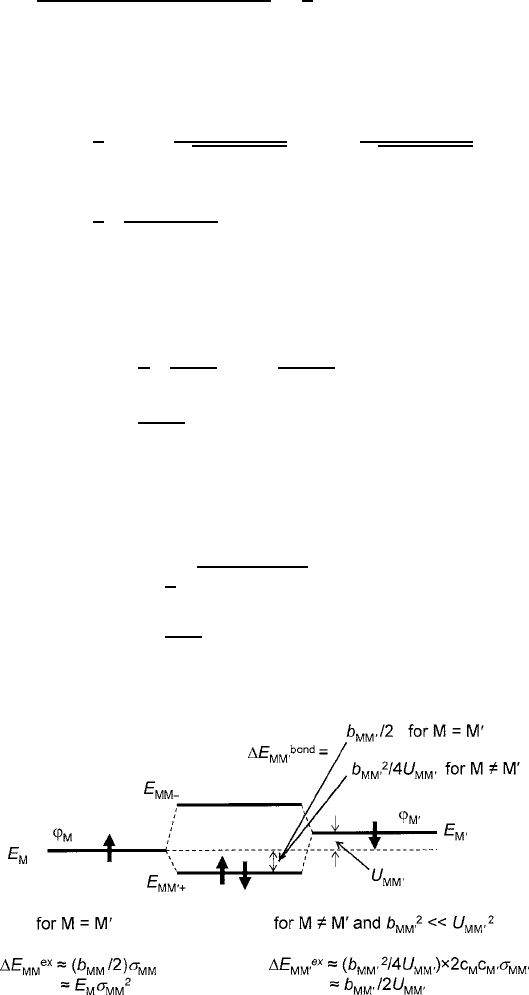
112 3 Magnetic Exchange in Oxides



MLM





C c



MLC

C c





C c



(3.3)

where



1 

C b

1 C

C b

1=2



C b



1=2

: (3.4)

For a magnetic oxide with strong ionic bonding, b

<< 1 and c



=2U

,sothat



MLM











for homonuclear M D M

: (3.5)

Thus, the effective overlap integral between M and M

can now be labeled as



D 

MLM

, and the simpliﬁed two-body problem depicted in Fig. 3.5 can be

solved with 

D c

M˙



˙ c



and a bonding stabilization energy

E

bond



C b



for homonuclear M D M

; (3.6)

Fig. 3.5 Two-body approximation to the metal–oxygen–metal molecular orbital extracted from

the upper half of Fig. 3.4

3.1 Interionic Magnetic Exchange 113

where b

D .E

C E

/

. Because only the delocalized fraction of the

3d spin population in

is required to satisfy Pauli spin pairing, the por-

tion of the covalent-bonding energy that stabilizes the antiparallel spin alignment is

weighted by the delocalized fraction 2c



.From(3.4)and(3.6)

E

D E

bond

 2c



C b



C b

1=2



; (3.7)

which is a ﬁrst-order function of b

In terms of the Heisenberg exchange energy between ions M and M

for com-

bined electron spins E

D2J

,(3.7) for a single orbital spin pair

where S

D 1=2 can be expressed as J

D b



. Because the screening

parameter h

MM0

is presumed to be positive based on the ground state spin occupa-

tion in Fig. 3.5, antiferromagnetism should prevail and J

would have a negative

other M and M

orbitals can compete, h

could be negative, causing an inversion

of the bonding/antibonding states and a weakening or even reversal in sign of J

leading to an antibonding ferromagnetic ground state.

To ensure the ferromagnetic alignment where b

MLM

is small, the missing con-

tribution from the e

repulsion would have to be introduced by a two-electron

exchange calculation, which would make a positive addition to the transfer element

and lead to a reversal in the cation–cation bonding/antibonding states '

and '



It is important to recognize that although these parameters are not the same as those

used in the more formal analysis of superexchange, at a qualitative level the model

provides helpful insight as well as providing an estimate of the effective transfer

integral b

. It also allows the addition of competing direct cation–cation b inte-

grals to arrive at a combined result. A comparison of the two approaches is offered

in the next section. Recall also that since b

varies directly as the ﬁrst power of the

overlap integral 

, by deﬁnition in (2.38), both 

and the quasi-direct trans-

fer integral b

are proportional to 

as indicated by (3.5). When the actual

exchange stabilization energy E

in (3.7) is considered, its dependence on the

cation–anion orbital overlap becomes 

, as pointed out also by Ballhausen [4].

This high sensitivity of the indirect exchange coupling conﬁrms that the stability

of long-range spin ordering in a crystal lattice is severely diminished by magnetic

dilution.

3.1.2 Valence-Bond Solutions

Analysis of interionic electronic and magnetic properties in ionic crystal lattices

by the molecular-orbital (MO) approach is largely conceptual, based on probabi-

lity estimates of the ground-state electron spin occupancy. As the name implies, a

114 3 Magnetic Exchange in Oxides

molecule is ﬁrst built from the strong Coulomb electric ﬁelds between cations and

anions, and then as demonstrated in the previous section, a second cation is added

to estimate the strength of magnetic exchange coupling that is more than an or-

der of magnitude weaker than the electrostatic bonding. Because the stabilization

from electronic hybridization is controlled by the wavefunctions overlap volumes,

the orbital overlap integral  represents a measure of the delocalization and is re-

tained explicitly in the formalism. In its purest form, however, the method does not

readily extend to collective electron situations unless the presumption of long-range

homogeneity allows the adoption of Hartree-Fock formalisms that lead to band mod-

els. An important feature of the MO approach is the preservation of the internal

electronic energy-level information of local cations from which the sensitivity of

the orbital angular momentum to lower symmetry crystal ﬁelds affects the multi-

plet structure that in turn determines the local magnetoelastic, magneto-optical, and

magnetic relaxation properties.

For the discussion of speciﬁc molecules, particularly as their complexities in-

crease, the more rigorous valence-bond (VB) approach offers a more quantitative

methodology [5]. Computation of bonding and exchange energies for speciﬁc

structures can be carried out by a method that allows the introduction of multi-

electron wavefunctions and includes the mutual electron repulsive energy e

A two-electron Hamiltonian that retains the nuclear and electronic interactions

is a convenient starting point. The effects of crystal ﬁelds on the partially ﬁlled

d -electron states can also be included if the appropriate molecular orbitals are em-

ployed as the starting wavefunctions. For the analysis of direct magnetic exchange

(applied originally to the H

molecule [1]), the valence-bondmethod is used to com-

pute the orbital interaction energies that dictate the high-spin (parallel) and low-spin

(antiparallel) states based on the indistinguishability requirement (Pauli principle)

of the two electrons sharing hybrid orbital states of both atoms. For this purpose,

the Coulomb energy terms E

and E

of (3.1) are replaced by the actual interionic

electron–nuclear attraction and electron–electron mutual replusion terms similar to

obtain a two-electron Hamiltonian H D H

C H

,where

D



„









;

D



: (3.8)

In the MO solutions, such as the hydrogen molecule ion sketched in Fig. 3.6a, H

contains only the nuclear terms. Under this restriction, the results for the MO and

VB methods are usually identical. However, that quickly changes when the electron

correlation energy is introduced in a formal manner. As deﬁned in Fig. 3.6b, the

distances r

and r

are the electron–nuclear separation of the exchanged electrons

labeled 1 and 2 on nuclei a and b, respectively, and r

is the separation between the

electrons themselves. Two-electron degenerate eigenfunctions '

D '

(initial

occupancy) and '

D '

(exchanged occupancy) of this Hamiltonian are con-

structed from products of single-electron functions for computation of the matrix

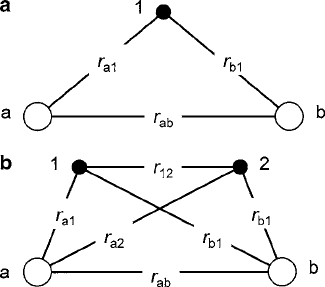
3.1 Interionic Magnetic Exchange 115

Fig. 3.6 Electrostatic

linkages between nuclei a and

bandelectrons1an2for(a)

the single electron hydrogen

molecule ion H

,and(b)the

hydrogen molecule H

elements K

.Coulomb/ Dh'

i and J

.exchange/ Dh'

i of the

2 2 Slater determinant described in Sect. 1.3. The solutions of the secular equation

give bonding and antibonding states energies according to K

˙J

. Consequently,

the sign of J

determines whether the spins in the ground state are parallel .S D 1/

for J

>0, or antiparallel .S D 0/ for J

<0.

The computation of J for a superexchange coupling between two magnetic ions

(spin cations) M

and M

bonded to a common O

2

ligand begins with the

assumption that unﬁlled orbital states are present in the M

–O–M

molecule. Since

the electrostatic stabilization among ions is maximized if the oxygen ligands carry

2– charges, meaning that the oxygen 2p band is ﬁlled, the unpaired electron spins

reside on the metal cations. Because of the ionic character of the bonding and the

important inﬂuence of crystal ﬁelds that remove the degeneracies of the 3d shell

states, as described in Chap. 2, the analysis of the interactions between M

and M

are treated on an individual orbital state basis.

A physical rationale is proposed to serve as a basis for superexchange second-

order perturbation analysis, which requires the existence of an excited state that

can be mixed with a state of lower energy by the electrostatic perturbation of

the molecular bonding, i.e., a nonzero off-diagonal matrix element created by a

transfer integral, to produce separate bonding and antibonding states. Maintain-

ing observance of the Pauli principle, the model sketched in Fig. 3.7ashowsthe

transfer of spins from the O

2

2p states onto the unﬁlled orbitals of the cations

to produce stabilization of an antiferromagnetic state between the spins localized

on the two cations through the creation of a virtual excited state energy U .Ini-

tially both spins are resident on the respective cations, with the relevant 2p orbital

state of the O

2

ion ﬁlled. The excited state is postulated by creating a virtual

transfer of the M

spin to the equivalent M

orbital state, resulting in the reaction

C M

! M

.nC1/C

C M

.n1/C

C U. A return reaction in the will com-

plete the transfer of spins from '

D '



(initial occupancy) to '

D '

(exchanged occupancy), and stabilize antiferromagnetic spin alignment.

If the starting wavefunctions are molecular orbitals that reﬂect the effects of the

cross electron–nuclear terms of (3.8), the electrostatic perturbation H

can now be

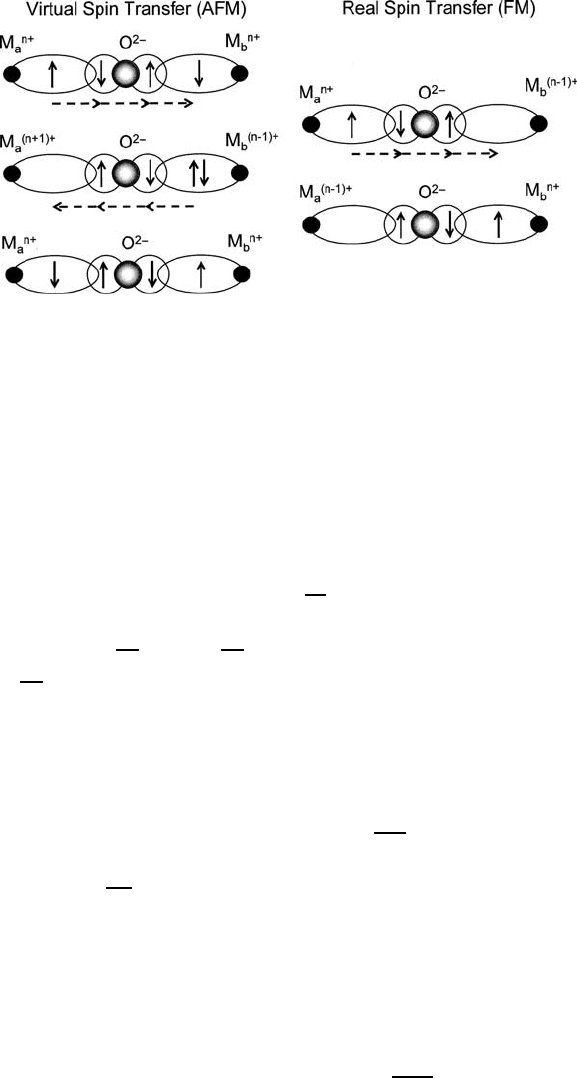
116 3 Magnetic Exchange in Oxides

Fig. 3.7 Tutorial illustration of superexchange virtual and real spin transfer: The former produces

antiferromagnetism, the latter, somewhat weaker ferromagnetism accompanied by electrical con-

ductivity

approximated by the e

electron repulsion term. This approach was used by

Anderson in his original formalization of the superexchange interaction [6]. For

apairof3d orbital states of cations linked by a 2p orbital of an oxygen ligand,

second-order perturbation theory is applied to the system to compute the energy

of the stabilized ground state. The standard correction to the orbital ground-state

energy for the orbital energy is then

E D

; (3.9)

where b



, U D



,and

exp.r

/, with  as a screening parameter [7]. After the addition of

the electron spin exchange operator s

 s

of negative sign (for antiparallel align-

ment) from Anderson’s formal solution by second quantization theory and the use

of the four Fermi spin operators to account for the two anion spins occupying the

2p orbital, (3.9) becomes

E

virtual

D2J

virtual

 s

D 2

 s

; (3.10)

where J

virtual

D

. This result has the reverse sign from the ﬁrst-order result for

direct exchange

E

direct

D2J

direct

 s

; (3.11)

where J

direct

>0.

In generalized format for n orbital levels linking two cations i and j,theex-

change stabilization energy derived from the spin operator part of (3.9)is

E

virtual

D2J

virtual

 S

D 2

 s

; (3.12)

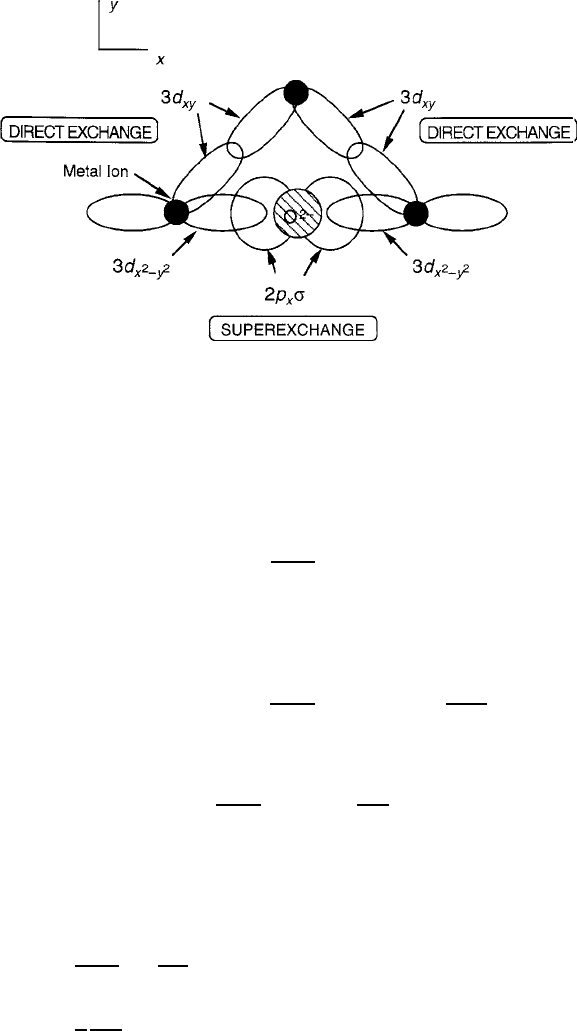
3.1 Interionic Magnetic Exchange 117

Fig. 3.8 Metal–oxygen exchange bonding showing the comparison between direct and indirect

or superexchange. Superexchange stabilizes antiferromagnetism; direct exchange is commonly

ferromagnetic

where J

is the direct exchange contribution suggested by Fig.3.8. If ions have total

spins S

and S

summed over n orbital states with s

D s

D 1=2, we can write

 s

 S

; (3.13)

and the combined exchange constant for the molecule is determined by applying

(3.11)and(3.12):

D J

direct

C J

virtual

ndirect



;

or simply







; (3.14)

where the subscript in (3.12) have been replaced by n for the parameters J and b.

For superexchange, we can extract from (3.12)forS

D S

D S,

virtual

D

virtual



for n equivalent orbital states with equal S D n=2; (3.15)

118 3 Magnetic Exchange in Oxides

Table 3.1 Bonding and exchange parameters

Molecular orbital(MO) Valence bond(VB)



0.3



10 eV b

 1:5 eV

–E

15 eV U

i15 eV

10Dq

=4U

D 1:7 eV



=2U



 0:1



2 eV

E

Super

1=2

0:1 eV

n D 1

E

Super

0:1 eV

n D 1

Super



D0:19 eV

n D 1

Super

1=n

D0:2 eV

n D 1

Per e

orbital in an octahedral site, 180

bond angles

D10eV , E

D25 eV

These values are on the order of ionization potentials and electron afﬁnities. See Ref. [7]

and we can also write

E

virtual



n

: (3.16)

The details of the quantum mechanical solution that include the explicit representa-

tion of the Fermi spin operators that control the alignment of the respective electron

spins s

and s

vectors are discussed in many standard texts [7, 11] and will not be

repeated here. However, it is important to compare the initial assumptions of the

MO and VB models and how they inﬂuence the results relevant to crystal ﬁeld and

magnetic exchange energies (Table 3.1).

In typical situations, the spin directions are not precisely aligned, but form an

angle 

with each other. To introduce this angular dependence into Anderson’s

result, the use of the exact relation for the scalar product S

 S

is not convenient

because of the quantum correction S.S C 1/ in the angular momentum addition.

If the Ising approximation is adopted, whereby only the z components of S are

retained in the vector product, S

D S cos







and the exchange energy for two

spins with z

equivalent neighbors can be expressed as

E

ferro

.VB/ D2z

 S

D2z

cos







Dz



1 C cos 



; (3.17)

There is a distinction between U

in the MO case and U of the VB method. In the MO case,

represents the in-lattice difference in energy between the two outermost electrons that remain

with their parent ions, and exchange is viewed simply as a small ﬁrst-order perturbation without

allowing for the formation of new ionic states by formal charge transfer. In the VB case, an exci-

tation deﬁnes U as the net change of two ionic stabilization energies involved in the virtual spin

transfer, approximated by the difference in the ionization potentials between the initial and ﬁnal

valence states of the ions. Here the perturbation is treated mathematically as second order.Asa

result, U

 0 in the localized MO treatment for like cations M D M

, but for the virtual spin

transfer of the VB method, U ¤ 0.SeeTable 3.1.

3.1 Interionic Magnetic Exchange 119

and for the antiparallel case,

E

antiferro

.VB/ D2z

 S

2z

sin







(3.18)

D z



1  cos 



To provide stabilization for ferromagnetism (

D 0), J

>0and for antiferro-

magnetism





D 



, J

<0. From this general result, the various spin ordering

situations that occur in transition-metal oxides can be examined.

This result was also obtained by Goodenough [7], who reasoned that Hubbard’s

exchange integral b

[12] could be modiﬁed to obey the Pauli exclusion principle by

constructing a transfer integral t

for a particular pair of orbital states that included

the canting angle 

between ionic spins. For this exercise, the relations are t

cos







and b

sin







for antiparallel and parallel alignment, respectively.

Installation of the t

expressions in place of b

in the superexchange terms of (3.12)

will yield results equivalent to (3.17)and(3.18).

If the MO model is used, the transfer integral is a ﬁrst-order perturbation and the

respective relations of (3.17)and(3.18) simplify to

E

.MO/ D2z

cos 

; (3.19)

where parallel alignment (

D 0) requires J

>0, and antiparallel alignment





D 



sets J

<0. This approach can be simply the analysis when ﬁrst-order

double exchange interactions are also present.

3.1.3 Spin Alignment in Oxides

The foregoing analyses for estimating spin alignment can be summarized. Ferro-

magnetism (parallel spins) occurs when the collective electron repulsion energy





is dominant in H

of (3.8). This is expected when the nuclear separa-

tion r

is large enough that the electron orbits overlap enough to disperse the spins

according to Hund’s rule without being unduly inﬂuenced by the attraction ﬁelds of

their opposite nucleus (antibonding state is lowest). To comply with (3.12), this con-

dition requires that J>0. It should be noted in Fig. 1.12 that the light members of

the 3d series provide fewer numbers of electrons to screen the attractive effects of

the nuclei for ferromagnetism to occur. This observation is also consistent with the

shorter bond lengths found for Ti, V, Cr, and Mn. Antiferromagnetism (opposing

spins) occurs when the interionic electron–nuclear terms of (3.8) are dominant in

. This is expected when the nuclear separation is small enough that the electron

charge clouds overlap greatly .r

<< r

/ and the dispositions of the spins are

controlled by the attractive ﬁelds of the opposite nuclei (bonding state is lowest). For