Dionne G.F. Magnetic Oxides

Подождите немного. Документ загружается.

120 3 Magnetic Exchange in Oxides

this case, the electrons can be more stable by ﬁlling states as spin pairs according to

the Pauli principle, and J<0. Experimental results that support these predictions

are shown in Fig.1.12 for a variety of direct exchange coupled compounds [13].

In oxides and other ionic compounds, the magnetic ions are not usually nearest

neighbors. Therefore, any direct exchange effects should be weak. If the collective-

electron formalism that is successful for metals is applied to oxides, r

and r

are

seen as too large to create a negative J , thereby predicting that a weak ferromagnetic

spin alignment might be expected. However, in most instances, this conclusion is not

supported by experiment. The cation spin ordering is most often antiferromagnetic.

Following the early suggestion of Kramers [14]thatindirect exchange must occur,

the general concept sketched in Fig. 3.1d was adopted. Indirect or superexchange is

the coupling of cations spins through the medium of nearest-neighbor anion ligands.

Ferromagnetism can also be produced by direct exchange .J > 0/ between next-

nearest neighbors, however,shown as 3d

orbitals overlapping across the diagonals

of a two-dimensional model, for example, a cube face.

In addition to the mechanism where spins of like cations with half-ﬁlled orbitals

correlate through common ligands by virtual charge transfer of two electrons in

a periodic structure to produce antiferromagnetic order analogous to itinerant fer-

romagnetism in metals, real charge transfer between dissimilar ions can induce

ferromagnetism by the sharing of a single electron. Because the spins are initially

local to their parent ions, these short range transfers are commonly described as

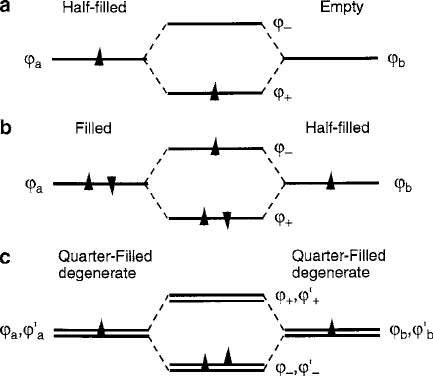
delocalized or semicovalent. Figure 3.9 illustrates two delocalization conditions:

(a) half-ﬁlled to empty and (b) ﬁlled to half-ﬁlled orbital transfers [15]. A spe-

Fig. 3.9 Molecular-orbital diagrams of ferromagnetic superexchange: (a) delocalization from

half-ﬁlled to empty, (b) delocalization from ﬁlled to half-ﬁlled, and (c) Hund’s rule ferromag-

netism in quarter-ﬁlled degenerate orthogonal metal–ligand states

3.1 Interionic Magnetic Exchange 121

cial case of ferromagnetic delocalization exchange

occurs between neighboring

cations of the same atomic element occupying identical lattice sites, but with dif-

ferent valence charges. When this mechanism operates in an antiferromagnetic or

ferrimagnetic system in which opposing magnetic sublattices are present, the trans-

fers are intrasublattice (homonuclear, H

for the active orbital), and the resulting

energy stabilization is called double exchange [16–19].

A somewhat related situation can occur in crystal ﬁelds (cubic, trigonal, or tetrag-

onal) that allow orbital degeneracy to survive unquenched. In Fig. 3.9c, a single

electron occupying a doublet, for example the t

spin-orbit stabilized case of d

in a c=a < 1 tetragonal site, presents a degenerate antibonding state that allows

Hund’s rule to be sustained and provides metallic ferromagnetic superexchange.

A fourth type of indirect exchange occurs where the spins couple to each other

through polarization of the “charge clouds” of their mutual environment rather than

by a formally deﬁned covalent bond. This mechanism, called RKKY after its col-

lective authors Ruderman-Kittel [20], -Kasuya [21], and -Yosida [22] and described

in most standard texts on magnetism, is generally associated with the rare-earth

or lanthanide series where the 4f

states are denied direct exchange interactions

with like-orbital states of neighboring cations or with crystal ﬁelds of anions by

the shielding from ﬁlled outer shells. Unpaired electron spins of the partially ﬁlled

inner shell interact indirectly with the immediate ligand ﬁeld by polarizing

the charges of their ﬁlled outer 5s

and 5p

shells that provide shielding from the

crystal ﬁelds of the ligands, as evidenced by the weaker superexchange effects of

rare-earth ions when occupying the c sublattice of magnetic garnets.

3.1.4 Ferromagnetism by Spin Transfer

Although less important from a purely magnetic standpoint, the case of real transfer

by delocalization is of interest because of the electrical conductivity implications

[3]. In the analysis of the magnetism created by a single mobile spin, it must be

recognized from the outset that there can be no spin-dependent stabilization asso-

ciated solely with the transfer between the two orbital states. However, if the two

cations each have a net spin or reside in a cluster of lattice spins that would provide

an exchange ﬁeld to dictate the orientation of the transferring spin, the net spins

of the cations involved in the transfer would likely be ferromagnetically aligned.

Otherwise the transfer electron would undergo a spin reversal to obey Hund’s ﬁrst

As a primer to the terminology used in the discussion of magnetic exchange in insulators,

we ﬁrst deﬁne two-electron exchange as virtual (spins do not actually switch nuclei) and

therefore covalent, with correlated spins to create antiferromagnetic order by correlation ex-

change, or simply superexchange. One-electron semicovalent exchange is described as real

(since the spin can actually switch nucleus) with delocalized spins to create ferromagnetic order

exchange.

122 3 Magnetic Exchange in Oxides

rule, violating the S D 0 requirement. If the spin retains its orientation in oppo-

sition to the polarization dictates of Hund’s rule, its energy of the e

repulsion

represents a destabilization that would offset any antiparallel alignments that are fa-

vored by unpaired spins occupying other orbital states on the same ion. The result

of an antiparallel alignment between the cations would be the discouragement of the

spin transfers through the creation of a spin trap or magnetic activation energy that

would result in a loss of the energy that would otherwise be gained by the sharing

of the spin.

As a consequence, in cases where only one of the orbital states is half-ﬁlled,

the Pauli principle is no longer the main concern because only one electron can be

involved in the coupling, and the two-electron exchange effects do not apply. Be-

cause the second orbital would be either empty or ﬁlled with no net spin in either

case, the e

repulsive term is not involved in the charge transfer. For practical

purposes, it can be convenient to view these two orbital combinations as analogous,

with electron transfer into the empty orbital and “hole” transfer into the ﬁlled or-

bital. Except for the extremes of d

, d

or certain low-spin conﬁgurations that are

diamagnetic because of low-spin S D0 conﬁgurations, Hund’s rule is followed for

ions with S D0 to prevent the loss of transfer energy that would otherwise occur

through the formation of excited states within the 3d-electron shell.

The various superexchange interactions between magnetic cations involve an-

ion mediation and can be described in greater detail. Two basic situations can be

expressed in chemical ionic notation as follows:

1. Two-electron covalent exchange (superexchange) occurs between half-ﬁlled or-

bitals depicted in Fig. 3.10a, where an electron from cation M

is undergoes a

virtual transfer to cation M

, requiring an excitation energy U according to

C M

! M

.nC1/C

C M

.n1/C

C U

followed by a corresponding return transfer of the electron from M

back to

to complete the exchange. Here U is for the general case of dissimilar ions

of the same valence charge. The term correlation is frequently used to describe

the antiparallel spin alignment that occurs cooperatively on opposite sides of the

cation–anion covalent bonds through virtual transfer mentioned qualitatively in

Sect. 3.1.1 and conﬁrmed by the analytical formalism [5–10].

2. One-electron semicovalent exchange occurs between dissimilar ions M and

(with d -shell occupancy differing by only one electron spin) through real

spin delocalization between half-ﬁlled ! empty or ﬁlled ! half-ﬁlled orbital

combinations:

C M

.nC1/

C!M

.nC1/C

C M

C U ˙ U

;

where U

is the adjustment for internal exchange energy of spin stabiliza-

tion (or destabilization if a spin ﬂip is required) to comply with Hund’s rule

where unpaired spins occupy other states of the 3d shell, shown schematically in

Fig. 3.10b. If the spin transfers within a ferromagnetic conﬁguration, the M

state

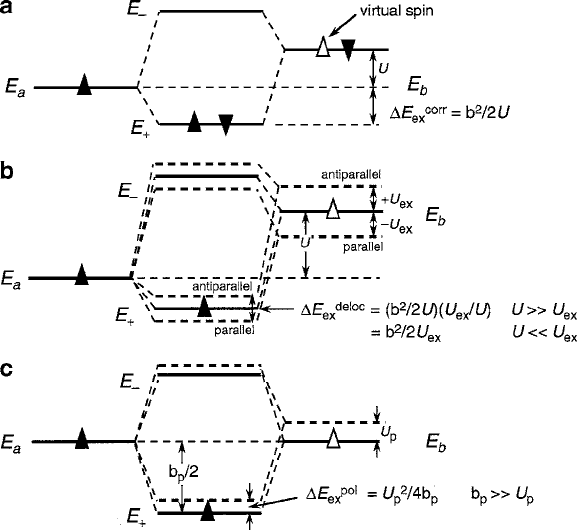
3.1 Interionic Magnetic Exchange 123

Fig. 3.10 Molecular-orbital diagrams indicating the origin of the exchange stabilization with

Aufbau spin order preferences indicated for: (a) of two-electron correlation antiferromagnetism,

(b) one-electron delocalization ferromagnetism (general case), and (c) one-electron delocalization

ferromagnetism, special case of mixed-valence charge transfer

becomes more stabilized by U

, which will tend to offset U .However,ifthespin

transfers within an antiparallel conﬁguration, the M

state becomes destabilized

by a similar energy.

General semicovalent exchange (Case 2) where the ions have different electron

conﬁgurations results from the delocalization of a single electron as described by

(2.46). Note that in its pure molecular form it is basically the H

molecule ion,

i.e., a one-electron case, but with U

added. This situation can occur with ions

of different atomic elements, e.g., Mn





and Cr





in octahedral ligand

coordinations. The energy reduction from the sharing of an electron between a half-

ﬁlled/empty hybrid state is also given by (3.16), but with half of the energy because

of one electron instead of two involved in the exchange. Since there is no a pri-

ori requirement for spin polarization, i.e., no electron repulsion within the hybrid

wavefunction, the amount of energy contributed by the transfer of the single spin

will be inﬂuenced by the established alignment of the other spins occupying the or-

bital states involved. However, if a spin ﬂip is necessary to complete the transfer in

compliance with Hund’s rule, the ionic transfer activation energy U

would be

increased instead of reduced by U

, thereby resulting in a lowering of the transfer

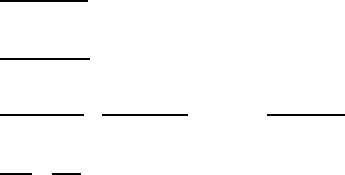
124 3 Magnetic Exchange in Oxides

probability and ferromagnetic exchange stabilization, as diagrammed in Fig. 3.10c.

The magnitudes of the respective delocalization exchange energies are given by

deloc



.U  U

.ferromagnetic system/

deloc



.U C U

.antiferromagnetic system/

E

deloc



.U  U



.U C U

D 2b



 U



(3.20)







for U

<< U

in agreement with Goodenough’s VB result [23]. As discussed in connection with

real spin transfer, E

deloc

represents an exchange trap energy for a mobile spin, e.g.,

a polaron with activation energy U

¤ 0. Typical values of the relevant parameters

are b 2 eV, U 15 eV, and U

 2 eV (Slater integral), which permit the

<< 1 requirement to be satisﬁed. If the initial energy of M

is restored in

the process by an accommodation of the spin orientation, U

then represents the

height of a barrier between two identical traps to be surmounted before a lossless

transfer is complete. With only one electron involved in the stabilization energy, the

MO orbital model can be used without loss of rigor.

In a special situation of Case 2 the combined energy of the initial and ﬁnal

states of mixed-valence M

and M

are unchanged in an adiabatic transfer event,

with the ions essentially exchanging positions in the lattice. In this situation, the

effect is called “double exchange” and occurs according to M

C M

.nC1/C

that is basically ferromagnetic as diagrammed in Fig.3.10c. How-

ever, the spin transfer still requires a mobility that is limited by an activation energy.

In real situations, the spin transfer is between mixed-valence ions of the same atomic

element, e.g., Mn





and Mn





or Fe





and Fe





.Themain

interest in these combinations is the promotion of ferromagnetism through spin

transfer (or vice-versa) by means of polaron carriers with mobility that is activated

by thermal hopping of electrons across energy barriers of height (or traps of depth)

generically deﬁned as U

D U

C U

. In special cases where exchange transfer

is strong and the trap depth is small, these effects can also be realized by covalent

tunneling through the bonding ground states. Here U

represents the trap energy

of a small polaron that results from adjustments of the local electrostatic (elastic)

environment [23].

For analytical purposes it is appropriate to introduce a polaron transfer integral

.Db

/ integral. For the case of b

>> U

, which is of interest for polarized spin

transport, the magnitudes of the contributions can then be deduced from the one-

electron molecular orbital solutions for double exchange from (2.46), noting that the

energies E

 E

D E

/2 in this limit. Here the extent of the exchange stabilization

that occurs because of the mutual ownership of the electron spin is determined by

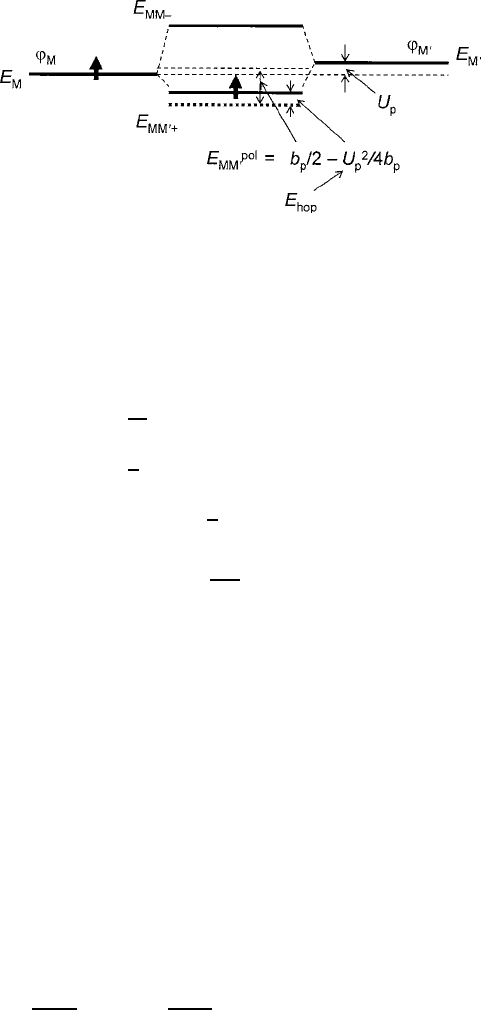
3.1 Interionic Magnetic Exchange 125

Fig. 3.11 Model of polaronic spin transfer indicating the origin of the E

hop

activation energy

the degree of sharing. When U

appears, both the sharing and stabilization decrease

accordingly. For a pair of identical orbital states, the analysis in Sect. 3.1.1 can be

applied to obtain the following relations

pol



.for U

D 0/;

pol





C U



1=2



for U



;

hop

D E

pol









1=2

 b



(3.21)





for b

>> U



;

where E

hop

is the effective polaron trap energy after U

is reduced by the transfer

integral b

in proportion to the ratio U

. The concept of polaronic electron spin

transfer is diagrammed schematically in Fig. 3.11; for a ﬁlled to half-ﬁlled hole

transfer, the mechanism is equivalent. This topic will be examined in greater detail

in Chap. 8.

3.1.5 Goodenough–Kanamori Rules

On the basis of the exchange energies of individual molecular-orbital states, rela-

tions for the total ionic exchange constants can be deduced by applying (3.14)to

combine the contributions from every occupied state. To this end, we deﬁne a resul-

tant exchange constant between ions i and j :

D

E

D



E

virtual



E

deloc



; (3.22)

126 3 Magnetic Exchange in Oxides

where E

virtual

and E

deloc

are for each individual orbital state and are positive

quantities by deﬁnition. In most cases, the ferromagnetic inﬂuence of the orbital

states linked by the single-electron transfers competes with the antiferromagnetism

of any lower energy half-ﬁlled orbitals. In octahedral sites, where t

orbitals form

weaker  bonds and e

stronger ¢ bonds, the resultant magnetic alignment will de-

pend on the particular ion combination. A more typical example is that of a d

–d

coupling between ions of the same atomic element. Here the ferromagnetic stabi-

lization of the single electron in the e

–p¢ state is offset by the antiferromagnetic

energies of the six t

–p electrons. The resultant spin alignments of these particu-

lar ions can assume parallel or antiparallel conﬁgurations depending on a variety of

factors [3].

For any superexchange combination M

–O–M

, estimates of the J

constant

can be made if values can be assigned to the b

integral and excitation energy U

for each participating orbital state. In analytical terms, we express (3.15)as

D





: (3.23)

This relation applies to any combination of 3d

ions. To make calculations, it must

ﬁrst be realized that three of the ﬁve d orbitals are t

–p and the other two are

–p¢. The distinction is important because the overlap integral 



is signiﬁcantly

less than 

. Estimates of these contributions that are made in Appendix 3A suggest

that b



 0:1.

With this ratio one can construct models for individual ion combinations to pre-

dict the likely net superexchange interaction. As an example, the relation of (3.23)

can be applied to the d

–d

case



to t



occupying adjoining octahedral

sites:

virtual









.antiferromagnetic/; (3.24)

or and for the single e

spin

deloc

C





.ferromagnetic/; (3.25)

which yields J

.antiferro/=J

.ferro/  –0:33 if the above ratio of b



is used.

Since the spin system can stabilize with either alignment, the

greater stabilization energy will determine which one will dominate, i.e., which one

will provide the larger spin-ordering temperature. The result for the above example

suggests a condition of ferromagnetism dominated by the delocalization exchange

from only one of the e

–p¢ bonds.

Note that if only one electron is stabilized in a semicovalent transfer, it could be argued that the

E

virtual

=E

deloc

is double at 0.2, which would result in J

antiferro

ferro

0:66.

3.1 Interionic Magnetic Exchange 127

By pursuing this reasoning to evaluate the probable spin alignments of various

combinations favored by particular cation–anion–cation linkages, a catalog of su-

perexchange interactions among members of the 3d

series can be created in-

cluding relative strengths of the expected J

constants. Such endeavors were

undertaken independently by Goodenough and Kanamori with results that have be-

come such valuable guidelines for the chemical design of magnetic compounds that

the Goodenough–Kanamori rules have been added to the lexicon. In Table 3.2,a

compilation of superexchange interactions based on Kanamori’s review [24]isre-

produced with some additions. The listing is restricted to some of the more standard

combinations, as examined by Anderson [6], Goodenough [25, 26], Anderson and

Hasegawa [18], and Slater [27]. Those with the same ionic valence are probably

more credible than the others because of more consistent values anticipated for b

and U .

Table 3.2 Summary of spin alignment estimates of d

ion 180

superexchange interactions in

octahedral sites (after Kanamori [24])

–d

Probable

combinations Cations Bond mechanism Spin alignment result

–d

–Mn

¢, -bonds

–Cr

A, G, A–H, S AF AF

–d

–Ni

¢-bonds

A, G, A–H, S AF AF

–d

–Mn

¢-bonds

–Fe

A, G, A–H, S AF AF

-bonds AF(weak)

G, A–H, S Uncertain

-bonds (Weak)

–d

–V

¢, -bonds

–Cr

A, G, A–H, S F F

–d

–Cr

¢-bonds

–V

A, G, A–H, S F F

–V

-bonds AF(weak)

–Cr

G, A–H Uncertain

-bonds (Weak)

A, S

–d

–Mn

Bond angle

–Fe

Dependent

–d

–Fe

¢-bonds

(e.g., FeO) A, G, A–H, S AF AF

–Co

-bonds Uncertain

(e.g., Co

(Weak)

–d

–Co

¢-bonds

(e.g., CoO) A, G, A–H, S AF AF

-bonds Bond-angle dependent

A Anderson mechanism; G Goodenough mechanism; A–H Anderson-Hasegawa mechanism;

S Slater mechanism

Not 180

bond angles

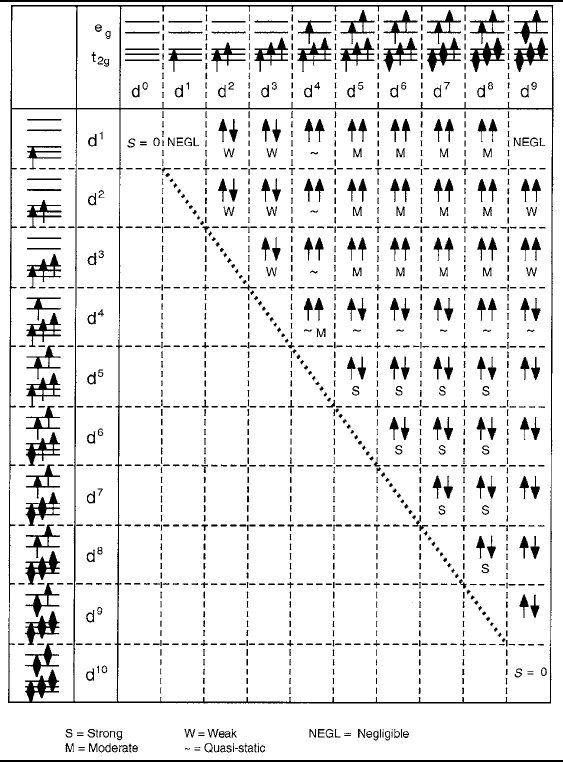
128 3 Magnetic Exchange in Oxides

Table 3.3 Spin ordering of d

ions in octahedral oxygen cites, high-spin states,

180

bonds (after Goodenough [28])

A more comprehensive study of cation combinations including those involving

low-spin conﬁgurations is given by Goodenough [28]. In Table 3.3 results for 180

bonds between cations in octahedral sites are presented. It is important, however, to

recognize that the spin ordering temperatures could be meaningful only where a ho-

mogeneous magnetic lattice is created. In most of these situations, particularly those

involving combinations far from the diagonal or of widely differing cation valences,

the actual materials structures may not be thermodynamically stable and may be

fashioned only through artiﬁcial procedures such as molecular beam epitaxial layer

growth. To estimate corresponding N´eel or Curie temperatures, the proper relations

between the spin values and the number of exchange coupled nearest neighbors must

3.2 Antiferromagnetism 129

Fig. 3.12 Model of the

Goodenough–Kanamori rules

of spin alignment for d

, d

and d

conﬁgurations in

octahedral sites. E

shell spin

reversal in d

is shown

intentionally to illustrate a

Hund’s rule violation

be selected for each pair of cations. An example of the application of these rules is

offered by the Aufbau models of superexchange couplings between the aforemen-

tioned d

–d

and d

–d

combinations sketched in Fig.3.12. As pointed out above,

the former favors ferromagnetism in one state of the e

shell that is opposed by all

three antiferromagnetic virtual states of the t

shell. In a charge-ordereddouble per-

ovskite lattice, e.g., La





, the result is largely inconclusive.

With Ni





in place of Mn

, however, all ﬁve orbital levels produce ferro-

magnetism that results in a Curie temperature near 300 K [29]. This subject will be

addressed further in Sect. 3.3.

Before the topic of the effective magnetic ﬁelds created by superexchange is

examined in the context of antiferromagnetism and ferrimagnetism, the implications

of tetrahedral sites and non 180

bond angles should be mentioned. Recalling the

discussion of the crystal ﬁeld parameter 10Dq and how it reverses sign between

octahedral and tetrahedral sites, we immediately recognize that the relative strengths

of  and ¢ bonds should be expected to change since the locations of the negative

anion charges are in the directions of the body diagonals in the tetrahedral case.

Where the bonds form other than 180

angles, the inﬂuence of the t

orbitals is

likely to increase relative to the e

orbitals. These subtleties will be discussed further

as the need arises in later chapters.

3.2 Antiferromagnetism

Because superexchange is generally associated with antiparallel spins, magnetic

oxides usually feature antiferromagnetic ordering. At this point in our discussion,

it is necessary to return to the subject of molecular ﬁelds introduced in Sect. 1.3

in preparation for a more detailed account of the opposing sublattice theories of

antiferro and ferrimagnetism.

3.2.1 Superexchange and Molecular Fields

One of the most important results of the insights gained into the relation between

covalent bonding and superexchange is the increased understanding of the origins