Dionne G.F. Magnetic Oxides
Подождите немного. Документ загружается.


442 8 Spin Transport Properties
proportionate decrease of the n
s
.T / and increase of the n
t
.T /. After rearrangement
to isolate n
e
s
.T /,(8.40) becomes
n
e
s
.T / D n
e
s
.0/
n
s
.T / n
t
.T
c
/
n
s
.0/ n
t
.T
c
/
: (8.41)
Based on this relation for the effective carrier density that contributes directly to the
supercurrent, the various London current and magnetic-field-related parameters can
be examined.
8.5.2 Condensation Energy
According to the London thermodynamic arguments, the condensation energy of
the superconduction transition is the reduction in the Gibbs free energy per unit
volume G D G
n
G
s
. According to the London thermodynamic arguments,
the condensation energy of the superconduction transition is the reduction in the
Gibbs free energy per unit spontaneous magnetism that was originally proposed by
London in defining his macroscopic molecule concept [90]. Unlike spontaneous
magnetism, however, there is no fixed population of dipoles and no strong ex-
change field that may lend itself to a Brillouin function variation with temperature.
Instead, the fractional population of superconducting polarons is exponentially de-
pendent on .kT /
1
, and since the polarons are transported by covalent transfer that
is not directly phonon-coupled to the lattice, the conduction mechanism is temper-
ature independent. This situation permits the electrostatic potential energy of the
dipole array to be released adiabatically as kinetic energy of carriers in an ordered
state (i.e., dynamic ferroelectricity), without the randomness of the thermalization
that produces the temperature change associated with the magnetocaloric or elec-
trocaloric effects.
Since condensation occurs as a supercurrent, a two-dimensional model is suffi-
cient to describe the physical situation. For a planar array of dipoles with moment
m
d
, G can be expressed as
15
15
This relation may be derived from the standard theory for the interaction energy density of a
dipole array (with K D 1)
E
d
D
X
j>k
"
m
j
m
k
r
3
jk
r
jk
m
j
r
jk
m
k
r
5
jk
#
;
where r
jk
is the distance between neighboring dipoles j and k. For the case of an x–y square-
planar array, we may consider the energy minimum to occur with the dipoles aligned with the
x-axis. E
d
in the x direction is 2m
2
d
=r
3
d
,inthey direction, Cm
2
d
=r
3
d
, and in the z direction, 0.
The net E
d
would then resemble (8.42). In general, lattice structure, as well as polaron dispersal,
must be examined to determine the best approximation for individual cases.
8.5 Supercurrents and Magnetic Fields 443
G
h
m
d
m
d
i
=KR
3
d
n
e
s
m
2
d
h
cos
i
=KR
3
d
n
e
s
: (8.42)
Since hcos iD1 (perfect alignment), R
s
D a= x
e
s
D a=n
e
s
V ,andm
d
D eR
d
=2
(at the midpoint between cell centers), (8.42) may be approximated by
G .1=4/
e
2
V=aK
n
e
s
2
.1=4/
e
2
=VaK
x
e
s
2
; (8.43)
where the minimum value of R
d
D R
t
D 2a asshowninFig.8.36b. For a D 4
˚
A,
K D 16, and recalling that V 1:7a
3
for La
2x
Sr
x
CuO
4
, it may be estimated that
G D 8:32 10
8
x
e
s
2
ergscm
3
. (For this computation and those that follow,
e D 4:8 10
10
esu:). Since x
e
s
is a function of T , G.T / may be evaluated at
T D 0. With x
e
s
.0/ D 0:068 for La
1:8
Sr
0:2
CuO
4
(see Fig. 8.27), G.0/ D 3:77
10
6
ergscm
3
;forYBa
2
Cu
3
O
7
,wherex
e
s
.0/ D 0:09 and V 1:5a
3
[considering
only the Cu(2) sites], and G.0/ D 7:54 10
6
ergscm
3
.
The formation of the spatially ordered carriers .rn
s
D 0/ in a molecular chain
results from the electrostatic dictates of the Madelung energy. For the creation of the
supercurrent, however, the dynamic order of the carriers results from electrostatic
repulsion between the mobile halves of the dipoles, possibly enhanced by the Pauli
principle repulsive action. As the carriers transfer between cells, maintaining the
required one carrier per cell ordering, there is no direct competition for quantum
states and the Pauli repulsion serves as a propellant to charge transport, rather than
as a cause of carrier scattering. As a consequence, supercurrent rigidity follows
naturally from the constraints of the directed bonding orbitals which act as inflexible
conduits for the passage of electrons.
8.5.3 London Penetration Depth
From the relation between current density and magnetic field stated in (8.28), the
London penetration depth is now defined in terms of n
e
s
, according to
L
D
mc
2
=4e
2
n
e
s
1=2
mc
2
V=4e
2
x
e
s
1=2
; (8.44)
which provides
L
.0/ D 5:32 10
5
V
1=2
x
e
s
.0/
1=2
cm, if the true electron mass
is used. For the La
1:8
Sr
0:2
CuO
4
perovskite in Fig. 8.27, V D 1:7a
3
, a D 4
˚
A, and
x
e
s
.0/ D 0:068, which yields
L
.0/ 2; 130
˚
A, in good agreement with the 2,000
˚
A
value determined from experiment [91,92]; for YBa
2
Cu
3
O
7
,whereV 1:5a
3
and
x
e
s
.0/ D 0:09,
L
.0/ 1; 740
˚
A, in accord with the 1,670
˚
A value derived from
microwave stripline resonance measurements [93]. The familiar ratio then reduces
to a new two-fluid function
Œ
L
.0/=
L
.T /
2
D n
e
s
.T /=n
e
s
.0/: (8.45)
444 8 Spin Transport Properties
From (8.38), (8.39), and (8.41), the following relation can be derived [72,94]
n
e
s
.T /
n
e
s
.0/
D
1 exp
E
hop
=kT
1 exp
E
hop
=kT
c
exp
E
hop
=kT
c
; (8.46)
which leads to
Œ
L
.0/=
L
.t/
2
D n
e
s
.t/ =n
e
s
.0/ D 1 exp .W W=t/; (8.47)
where t D T=T
c
.
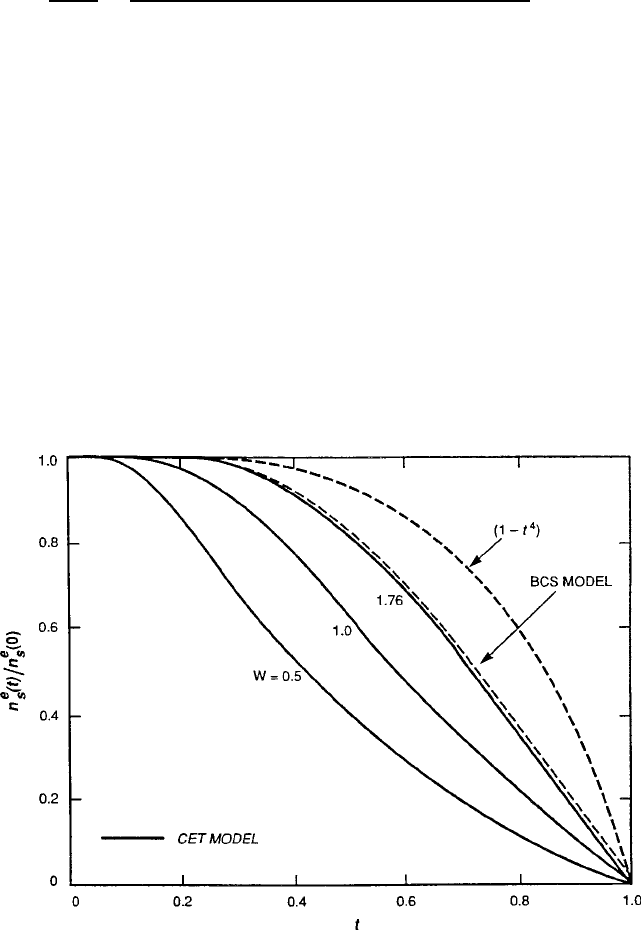
In Fig. 8.38, generic curves of n
e
s
.t/ = n
e
s
.0/ from (8.47) are plotted for a range of
W values [including W D 1:76, i.e., the universal ratio between kT
c
and the BCS
energy gap .0/], and compared with curves of the empirical two-fluid
1 t
4
and BCS models [95]. At this point, it is instructive to compare the basic critical-
temperature relations for the BCS and GET models:
kT
c
D .0/=1:76 .BCS/; (8.48a)
and
kT
c
D E
hop
=W .CET/: (8.48b)
Fig. 8.38 Comparison of n
e
s
.T /=n
e
s
.0/ vs. t for W D 0:5, 1.0, and 1.76 (BCS value), the actual
BCS function, and the empirical
1 t
4
two-fluid function. Figure reprinted from [94]permis-
sion.
c
1993 by the IEEE
8.5 Supercurrents and Magnetic Fields 445
With the La
1:8
Sr
0:2
CuO
4
and YBa
2
Cu
3
O
7
systems examined in Sect. 8.4, working
values of W determined from fits to data are 0.75 and 0.5, respectively. For the
BCS model, the denominator is the constant, 1.76, calculated from =,where
is Euler’s constant .D 0:577/. All of the material-related information is contained
in the gap parameter .T / computed at T D 0 that appears in the numerator. This
temperature-dependent gap energy, which determines the ratio of supercarriers to
quasiparticles (normal electrons), is a maximum at T D 0 and falls to zero in a
Brillouin-type curve as T ! T
c
. In the CET treatment, a “gap” equivalent would
be the fixed numerator E
hop
, but the denominator is also a material-related variable
that is strongly dependent on the polaron radius
p
. Although their meanings differ
somewhat, .0/ and E
hop
both represent energy separations (the former a conden-
sation gap for electrons paired in k-space and the latter a polaron trap barrier), the
important differences in the two relations of (8.48) also lie in the W parameter vs.
the fixed denominator 1.76 of the BCS model.
Although the regime in which the above analysis was focused is the “clean”
limit
0
L
of the high-T
c
superconductors, for completeness it is appropriate
to mention the relations for effective penetration depth and coherence length
that are used for the other classes of superconductors. For type-I pure limit with
0
L
(formally expressed as
3
0
2
L
), D 0:65
L
.
0
=
L
/
1=3
, and for the
type-II (London or dirty) limit where Ÿ ! ` (formally expressed as
3
0
2
L
,
D
L
.
0
=/
1=2
L
.
0
=`/
1=2
.
8.5.4 Critical Magnetic Field
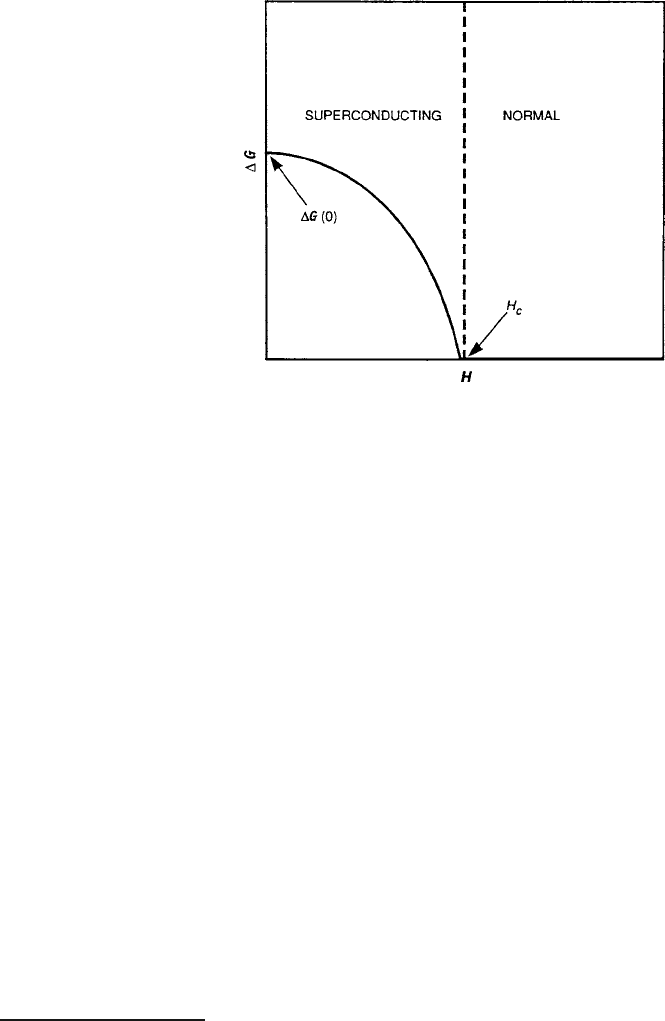
If a bulk specimen is placed in a magnetic field H , the field will be expelled from
the interior during a superconduction transition (the Meissner effect). Consequently,
the superconduction Gibbs free energy G
s
will increase by the amount of the energy
density H
2
=8 of the expelled flux [96]. As a function of H , G
s
becomes
G
s
.T; H / D G
s
.T; 0/ C H
2
=8: (8.49)
For a nonmagnetic specimen in the normal state, however, G
n
.T; H / D G
n
.T; 0/,
and since the condition for the return to the normal state is G
n
G
s
D 0, the critical
field may be defined according to Fig. 8.39 as
rG.T; 0/ D G
n
.T; 0/ G
s
.T; 0/ D H
c
.T /
2
=8 (8.50)
and
H
c
.T / D Œ8G.T; 0/
1=2
; (8.51)
where H
c
.T / is the value of H that (with i
s
) decays exponentially from the surface
according to exp.–x=
L
/ as determined by the solutions of (8.27). After substitution
from (8.43),
H
c
.T / D
2e
2
V=aK
1=2
n
e
s
.T / D
2e
2
=VaK
1=2
x
e
s
.T /: (8.52)
446 8 Spin Transport Properties
Fig. 8.39 Change in Gibbs
free energy as a function of
H , indicating a decreasing
energy available for
conversion to the kinetic
energy of supercurrent as
H ! H
c
[9]
To determine H
c
, the specimen cross-sectional area A should exceed the penetration
depth in order to avoid the necessity of a correction .1 A
eff
=A/
1=2
to the effective
volume of flux expulsion. If A
eff
=A ! 1,asinthecaseofafinewireorthinfilm,
the flux penetrates much of the material and the effective H
c
is substantially greater
than the true value.
From the estimates of G(0,0) beneath (8.43), substitution into (8.51) leads to
H
c
.0/ 10 kOe for bulk La
1:8
Sr
0:2
CuO
4
,andH
c
.0/ 14 kOe for YBa
2
Cu
3
O
7
.
An experimentally based value of 10 ˙ 2 kOe for bulk polycrystalline YBa
2
Cu
3
O
7
was derived from conventional theory [67].
A universal relation follows directly from (8.52):
H
c
.T /=H
c
.0/ D Œ
L
.0/=
L
.T /
2
D n
e
s
.T /=n
e
s
.0/ (8.53)
and
H
c
.t/ =H
c
.0/ D 1 exp .W W=t/ (8.54)
to produce a temperature dependence the same as the two-fluid function of (8.45).
The curves plotted in Fig.8.40 for W D 1:76 and 2 are therefore from the same
family as those of Fig. 8.38, but in this case it is more appropriate to compare them
with the standard thermodynamic relation H
c
.t/ =H
c
.0/ D
1 t
2
,
16
andalsoto
examine the slopes at T D T
c
. From the derivative of (8.54), it may be shown that
16
Note that the universal relations for H
c
.
t
/
=H
c
.0/ and
Œ
L
.0/=
L
.
t
/
2
are identical according to
(8.45)and(8.54), but differ in their thermodynamic counterparts (1 t
2
)and(1 t
4
), respectively.
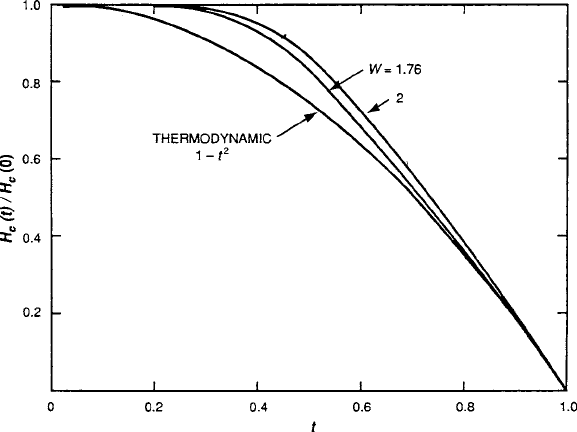
8.5 Supercurrents and Magnetic Fields 447
Fig. 8.40 Comparison of H
c
.
t
/
=H
c
.0/ vs. t for W D 1:76 (BCS value) and the thermodynamic
1 t
2
two-fluid function [9]
Œ@H
c
.t/ =@t
tD1
DH
c
.0/W (8.55)
or
@H
c
.T /=@T DWŒH
c
.0/=T
c
at T D T
c
: (8.56)
To match the slopes of the CET curve to the thermodynamic relation, W must equals
2 slightly larger than the 1.76 BCS ratio. As indicated in Figs. 8.38 and 8.40,the
curves fit well over the upper half of the t range. Based on these results, one con-
cludes that lower values of W substantially alter the shape of these curves, including
the appearance of a tail and an inflection point at t D W=2, i.e., concavity begins to
appear for W<2, and have an overall deleterious effect on the magnitudes of H
c
.
8.5.5 Critical Current Density
From the hypothesis of dynamic ferroelectricity, critical current may be defined by
equating carrier kinetic energy to condensation energy G.From(8.50)and(8.51),
the carrier kinetic energy [97] can be expressed as
G D .1=2/ n
e
s
mv
2
s
D H
2
c
=8 D .1=4/
e
2
V=aK
n
e
s
2
; (8.57)

448 8 Spin Transport Properties
and
v
s
D
.1=2/ e
2
V=maK
1=2
n
e
s
1=2
D
.1=2/ e
2
=maK
1=2
x
e
s
1=2
: (8.58)
For La
1:8
Sr
0:2
CuO
4
and YBa
2
Cu
3
O
7
, with a D 4
˚
AandK D 16, v
s
D 7:3 10
6
and 8:4 10
6
cm s
1
, respectively. Note that the relation v
s
K
1=2
is consistent
with the expected trends in local accelerating fields within materials of high or low
dielectric constant, i.e., metals or insulators.
Since the general supercurrent density i
s
D n
e
s
ev
s
, a critical current density
i
s
.D i
c
/ can be defined from (8.58)as
i
c
D
.1=2/ e
4
V=maK
1=2
n
e
s
3=2
D
.1=2/ e
4
=mV
2
aK
1=2
x
e
s
3=2
; (8.59)
For the La
1:8
Sr
0:2
CuO
4
and YBa
2
Cu
3
O
7
superconductors of Fig. 8.27 with K D
16, a D 4
˚
A, and V D 1:7a
3
and 1:5a
3
, i
c
.0/ D 3:67 10
8
Acm
2
and 6:33
10
8
Acm
2
as the upper theoretical limits correspondingto x
s
.0/ D 0:068 and 0.09,
respectively.
17
From (8.47), (8.59) may be converted to a universal curve,
i
c
.t/ =i
c
.0/ D Œ1 exp .W W=t/
3=2
: (8.60)
This relation is appropriate for film specimens where penetration depths exceed the
thickness. For bulk specimens or films with greater thickness, (8.60) can be modified
according to [98]
i
c
.t/ =i
c
.0/ D Œ1 exp .W W=t/
3=2
A
eff
.t/ =A
eff
.0/; (8.61)
which simplifies to
i
c
.t/ = i
c
.0/ Œ1 exp.W W=t/
3=2
L
.t/ =
L
.0/ Œ1 exp .W W=t/
(8.62)
In Fig. 8.41, the data of Lessure et al. [99] for a bulk YBa
2
Cu
3
O
7
specimen is
plotted and compared favorably with (8.62)forW D 1.
In an external magnetic field H , part of the condensation energy density H
2
=8
is required to expell H from the interior of the material as shown in Fig. 8.39,anda
more general expression for G .H / may be constructed from (8.50)and(8.51):
G .H / D G
n
.H / G
s
.H / D
H
2
c
H
2
=8: (8.63)
17
From (8.28) it will be recalled that i
S
D
c=4
2
L
A.IfA
c
H
c
L
(for specimens of di-
mensions greater than
L
), then (8.59) may be derived directly from the London theory, with
i
c
D
.
c=4
/.
H
c
L
/
.
1=2
/
e
4
=mV
2
aK
1=2
x
e
s
3=2
,after
L
D
mc
2
=4e
2
n
e
s
1=2
from (8.26)
and H
c
D
2e
2
V=aK
1=2
n
e
s
from (8.52) are substituted.
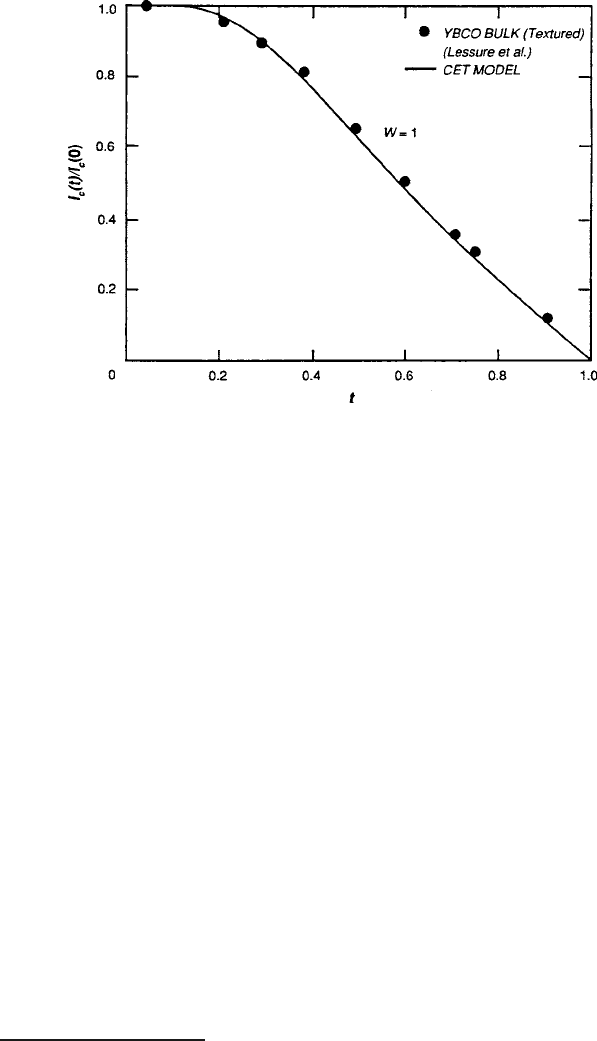
8.5 Supercurrents and Magnetic Fields 449
Fig. 8.41 CET universal plot of i
c
.
t
/
=i
c
.0/ for the bulk case with W D 1 [9], compared with
data of Lessure et al. [99]
From (8.58)and(8.63), (8.57) for the kinetic energy density may be generalized to
G .H / D .1=2/ n
e
s
mv
2
s
D
H
2
c
H
2
=8 (8.64)
If it is assumed that n
e
s
is unaffected by H ,
18
the reduction in G occurs as a de-
crease in carrier velocity and
v
s
D
H
2
c
H
2
=4mn
e
s
1=2
; (8.65)
from which a universal relation for critical current density as a function of magnetic
field may be deduced as
i
c
.H / =i
c
.0/
h
1 .H=H
c
/
2
i
1=2
(8.66)
Thus, it is seen that the supercurrent is limited by magnetic field which offsets the
condensation energy, and by temperature which controls the density of available
carriers.Note that (8.66) describes the situation in the absence of a fluxoid lat-
tice, i.e., type-I superconductors, where H
c
is the thermodynamic critical field, and
18
In type-II superconductors, there are situations where n
e
s
may be considered to be a function of
H , such that
L
.
H
/
!1as n
e
s
.
H
/
Dj
S
.
H
/
j
2
! 0 [100].
450 8 Spin Transport Properties
should not be expected to predict accurately the behavior of type-II superconductors,
in which a variety of magnetic-field-related effects may influence i
c
.t; H / [101].
Since T
c
DE
hop
=kW, the superconduction critical temperature may be increased
in two ways (1) by raising E
hop
, at the risk of introducing a magnetic exchange en-
ergy barrier that could upset the b E
hop
requirement and (2) by reducing W , either
through improved polaron dispersal .P ! 1/ or smaller polaron radii .n
t
! 0/,but
at the expense of lowering in a relative sense H
c
and i
c
as T ! T
c
.
8.5.6 Coherence Length
A natural segue from the discussion of critical magnetic fields is the subject of coher-
ence and its role in type-II superconductors. As discussed in Sect. 8.4.1, the notion
of coherence was introduced by Pippard [54], who proposed that the nonlocal na-
ture of the superelectron may be characterized in terms of the uncertainty principle.
In this approach as applied to free-electron systems, the superconducting electrons
are drawn from the population with energies within kT
c
of the Fermi level. In order
to obtain a relation for the individual carrier momentum p
s
in the superconducting
state, Pippard reasoned that their momentum range could be estimated by dividing
the condensation energy, assumed to be equivalent to kT
c
, by the Fermi velocity v
F
,
i.e., p
s
kT
c
=v
F
/ [102]. As a consequence, the position uncertainty (coherence
length) becomes x .D
0
/ .h=2/ .v
F
=kT
c
/.
Another definition of coherence length was provided by Ginsburg and Landau
(GL) from the solution of a Schrodinger-type equation with a nonlinear term [55].
The resulting aggregate eigenfunction for this differential equation contained an
exponential decay [see (8.31)], §
s
.x/ §
s
.0/ exp .–x=Ÿ/,where
j
s
j
2
D n
s
is the
expectation value of a spatially varying superconduction ensemble wavefunction of
coherence length that reduces to the Pippard result for T T
c
. Thus, conceptual
compatibility between Pippard and GL can be established if is the average distance
a carrier travels before losing coherence with the ordered state. In reality, the carrier
rarely reaches this limit, but the attendant velocity range defines the degree of spatial
order. In its essentials, the Pippard definition describes the coherence of a carrier
chain composed of wavepackets with a spatial profile that may be assigned a de
Broglie wavelength defined by
deB
D h=p
s
: (8.67)
This concept is compatible with the basic CET model of a chain of localized
wavefunctions that link to form a single molecular-orbital function. Applying the
uncertainty relation for space packets, we obtain
p
s
x h=2; (8.68)

8.5 Supercurrents and Magnetic Fields 451
or in this present context
p
s
0
h=2; (8.69)
where p
s
is replaced by p
s
.
19
In the CET model, the condensation energy is not immediately determined by
kT
c
, so the use of the above Pippard relation for p
s
must be modified. The role of
the energy trap is different from the conventional band theory approach in that it de-
termines directly the population of available supercarriers, but only indirectly their
energy. As discussed in Sect. 8.5.2, G is determined by n
e
s
.T / and is more closely
associated with H
c
than T
c
. Because the CET model has conveniently produced a
distinct relation for the carrier velocity, however, the question of estimating p
s
by
indirect means is unnecessary, and we may therefore define a coherence length sim-
ilar to that of Pippard directly from the relation for superconductor carrier velocity
of (8.58),
0
.h=2/ =p
s
D .h=2/ =mv
s
h
2
=2
2
me
2
.aK=V /
1=2
n
e
s
1=2
(8.70)
If the perovskite parameters from previous estimates, K D 16, V D 1:7a
3
,and
a D 4
˚
A, are applied to (8.70) (expressed in terms of x
e
s
),
0
.0/ 8 10
8
x
e
s
.0/
1=2
cm (8.71)
For x
e
s
.0/ D 0:068 .La
1:8
Sr
0:2
CuO
4
/ and 0.09 .YBa
2
Cu
3
O
7
/,
0
.0/ 32
˚
Aand
27
˚
A, respectively, in general agreement with experiment [103]. For type-I metal
superconductors, Ÿ
0
.0/ 10
4
˚
A, which is also consistent with (8.71) through the
direct dependence of
0
on the dielectric constant
K
1=2
that becomes very large
in highly polarizable materials with loosely bound electrons.
20
Since a discussion of the type-II superconductors will follow, it is appropriate to
establish the analytical relationship between
0
and
L
from (8.70)and(8.44):
0
D Œ
2h
2
=m
2
c
2
.aK=V /
1=2
L
; D
2 10
10
.aK=V /
1=2
L
cm; (8.72)
where lengths are expressed in cm. For the two perovskite systems
D
L
=
0
5 10
9
.aK=V /
1=2
; (8.73)
19
An alternative derivation of (8.69) may be obtained from a standard quantum mechanics op-
erator through the relation j
.
h=2
/
r
s
D p
s
s
,wherep
s
is a good quantum number for
a stationary state. Since the ensemble wavefunction
s
.
x
/
s
.0/ exp
.
x=
0
/
from (8.31),
r
s
D
.
1=
0
/
s
and we again arrive at p
s
0
h=2. This result suggests that the ensemble
concept of GL and the individual wavepacket idea of Pippard are equivalent as far as coherence is
concerned.
20
The dielectric constant in the context of conducting materials is viewed here as a parameter
that represents the polarizability in a quasi-insulating state, with at least some of the “free” elec-
trons condensed back on their parent ions for covalent transfer. In the metallic state, of course,
macroscopic polarization effects can only be inferred, since any measurements are precluded by
the presence of free electrons.
