Dionne G.F. Magnetic Oxides

Подождите немного. Документ загружается.

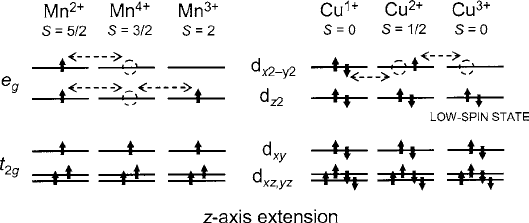
402 8 Spin Transport Properties

temperature, a metal–insulator transition takes place. Application of magnetic ﬁelds

large enough to inﬂuence the Curie temperature has been shown to produce dramatic

magnetoresistance effects – colossal magnetoresistance (CMR) [24]. To explain the

origin of this phenomenon, we ﬁrst examine the source of the ferromagnetic spin

alignment.

8.3.1 Manganese-Ion Exchange Interactions

For the basically cubic octahedral oxygen coordination, crystal-ﬁeld effects dictate

that the t

orbital states are of lower energy and are half-ﬁlled to satisfy the Hund’s

rule spin polarization requirement for both Mn





and Mn





. For each

combination of exchange linkages, the t

electrons produce weak antiferromag-

netism via covalent  bonding through the O

2

anions, e.g., Mn

–O

2

–Mn

For the Mn

–O

2

–Mn

combinations, the larger transfer integrals are the re-

sult of the stronger 180

¢-bonding in the e

states. A single electron in the e

shell (Mn

case) can be stabilized by a static Jahn–Teller (J–T) distortion that

splits energy levels as shown in Fig. 8.9. Where the distortions are cooperative, a

tetragonal/orthorhombic phase will appear (with site axis ratio c=a; b >1)andthe

half-ﬁlled d

orbital is stabilized relative to the empty d

y

state. Superexchange

spin ordering possibilities for this system were examined in a seminal paper by

Goodenough [25].

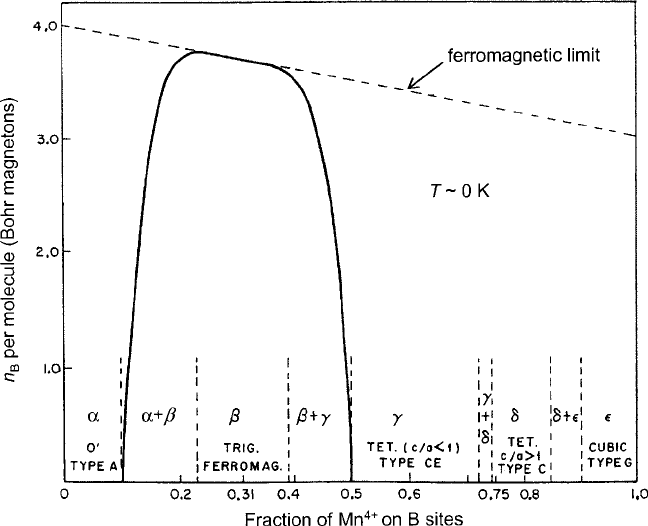
From the Curie temperature data of Jonker and Van Santen [26]for



1x



1x



presented in Fig. 8.10 with the various crystallographic

phases as a function of x [25], the variations in exchange ﬁeld with Mn

concen-

tration may be analyzed on the basis of changes in the nature of the J–T effect.

At x D 0, the J–T effect should be mainly static and cooperative, favoring an

orthorhombic distortion and antiferromagnetic order in most cases. With increas-

ing Mn

concentration, ferromagnetism dominates in the regime up to x D 0:5,

with a peak near x D 0:3.AsMn

ions are introduced, parallel spin alignments

Fig. 8.9 Schematic diagram of delocalization exchange in the e

shell, comparing the various

cases of mixed-valence Mn and Cu

8.3 Magnetoresistance in Oxides (CMR) 403

Fig. 8.10 Plot of Curie temperature vs. x for



1x



1x

with various crys-

tallographic phases indicated. Model is adapted from original data of Jonker and Van Santen [26]

presented in Fig.3.22. Figure reprinted from [25] with permission.

1955 by the American Phys-

ical Society. http://link.aps.org/doi/10.1103/PhysRev.127.2058

result from a combination of factors (1) the Mn

–O

2

–Mn

couplings contribute

ferromagnetism by charge transfer among half-ﬁlled/empty orbital combinations as

studied by Zener [27] and de Gennes [28] and (2) the anticipated antiferromag-

netism from the Mn

–O

2

–Mn

couplings in a static J–T effect is converted to

ferromagnetism possibly by vibronic-induced J–T effects proposed by Goodenough

[29–32] that alternates the order of the e

–2p¢ antibonding levels (bands) and al-

lows the two e

electrons to be stabilized with parallel spin alignments in separate

molecular-orbital states.

Ferromagnetism can therefore occur because of the absence of static tetrago-

nal deformation that leaves the e

states degenerate and removes the necessity for

Pauli spin pairing, similar to the t

degeneracy in the case of CrO

discussed pre-

viously. As illustrated in Fig. 8.11, in cases where the Mn

–O

2

–Mn

couplings

dominate and the electronic bandwidth is broad enough for the interactions to be

collective, a ligand vibronic mode may cause the d

and d

y

states of adjacent

Mn cations to oscillate out of phase and form a quarter-ﬁlled e

shell. This situation

allows Hund’s rule to apply and gives rise to ferromagnetic order and spin-polarized

metallic conductivity. The quasi-static J–T effect is consistent with the absence of

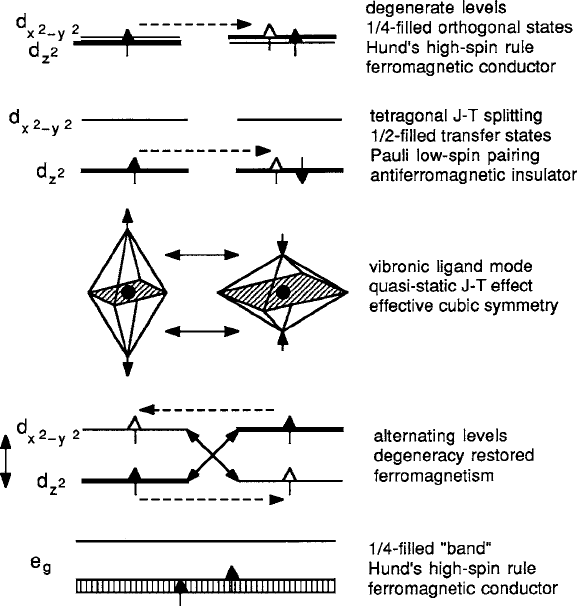
404 8 Spin Transport Properties

Fig. 8.11 Schematic diagrams of J–T effects, including the quasistatic case in which carrier trans-

fers into empty e

orbital states that are mixed by vibronic modes may cause ferromagnetism

the static orthorhombic distortion in the regime of the observed ferromagnetism that

would normally be expected to stabilize the e

electron of the Mn

ions in the

lower of the split e

states. This condition would tend to deny tunneling transfer by

increasing the spin-dependent part E

hop

of the polaron trap energy. The anticipated

couplings for the various combinations were summarized in Chap. 3 (Table 3.7).

Above x  0:1, the vibronic actions can inﬂuence a change in crystallographic

phase from orthorhombic to cubic or rhombohedral (trigonal), thereby restoring the

degeneracy of the e

levels in the crystal ﬁeld, and remaining such until x ap-

proaches 0.5. In some cases the vibronic effect on e

can occur in the presence of

an orthorhombic bias. With half the Mn ions in the 4Cstate, the quasi-static behav-

ior breaks down as the lattice symmetry returns to orthorhombic. At this point, the

levels are split, and the remaining Mn

–O

2

–Mn

couplings revert to anti-

ferromagnetism, combining with the existing antiferromagnetic Mn

–O

2

–Mn

couplings to produce various cation charge order and antiferromagnetic conﬁgu-

rations in the range from 0:5 < x < 1:0. It should also be pointed out that in

8.3 Magnetoresistance in Oxides (CMR) 405

the ferromagnetic region the maximum available m

per formula unit is apparent

at cryogenic temperatures, conﬁrming the anticipation of complete uncanted spin

polarization similar to that of CrO

To account for the magnetic exchange effects that produce the observed ferro-

magnetism, a single magnetic lattice is assumed. Because both the carrier charges

are among the d electrons that provide the magnetic moments, the disposition of

spins cannot be static. Valence-charge ordering may occur coincident with spin or-

dering in spatially variable phases, which could explain the reported observation

of a metal–insulator mosaic that probably corresponds to ferro/antiferromagnetic

domain patterns [33]. To describe this system by traditional analytical methods

is a formidable challenge. Nonetheless, a model based on a random distribution

of Mn

and Mn

cations carrying spins S

and S

can be fashioned. For this

exercise, three exchange interactions are deﬁned: J

 S

, J

 S

,and

S

.orJ

 S

/, from which an effective exchange energy is constructed

for use with the Brillouin–Weiss theory.

For an individual charge transfer between Mn

and Mn

ions, (8.1) can be

applied to express the activation energy as

.

/ D zJ

 S

 zJ

.1 C cos

/; (8.20)

where z is the number of nearest neighbors and 

is the average angle between

the Mn

and Mn

spins which will be assumed to be simply , the average angle

between adjacent spins within the entire system. When  D 0, E

is a maxi-

mum, the spins are collinear, and the S D 0 requirement for the charge transfer is

satisﬁed. If >0, E

decreases and energy must be provided to restore the spin

alignment and maintain S D 0. According to (8.1), the additional energy has the

effect of a magnetic trap of depth

hop

D E

.

/  E

.0/ D zJ

.1  cos 

/; (8.21)

and E

hop

is also the activation energy necessary to effect the charge transfer be-

tween the two cation sites. It should be noted that 

values in the range 0 to 

areallowedby(8.21), and that the theoretical maximum activation energy from

exchange is actually 2E

hop

when the spins are antiferromagnetic. For the present

problem, however, the regime of interest is the ferromagnetic to paramagnetic tran-

sition that occurs at the Curie temperature where the average angle between spins

becomes =2.

8.3.2 Magnetoresistivity-Temperature Model

Since the Brillouin–Weiss function B

represents the average z-axis projection of

spins within a cone of half-angle , it also represents the average angle between a

spin and the direction of the exchange ﬁeld in which it resides. Consequently, cos 

406 8 Spin Transport Properties

in (8.21) may be represented by B

and the spin canting effect on the binding energy

can now be expressed as a function of temperature and magnetic ﬁeld.

The total activation energy as a function of temperature and magnetic ﬁeld H

may then be expressed in terms of molecular ﬁeld theory according to

hop

D E

hop

C E

hop

Œ1  B

.T; H / ; (8.22)

where E

hop

is the polaron trap energy in the absence of spin-polarization constraints

(chosen as 0.004 eV), and E

hop

0:1 eV) is the magnetic exchange contribution that

reaches its full value in this system when the spins become disordered at T>T

[34,35].

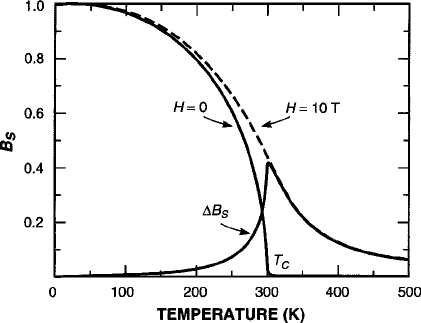
In Fig. 8.12, the Brillouin–Weiss function is plotted as a function of T for an aver-

age molecular-ﬁeld coefﬁcient N D 114 molcm

3

(derived from the J

, J

,and

parameters of the randomly dispersed Mn

and Mn

ions with x D 0:23),

resulting in a Curie temperature of 300 K. The effect of an external ﬁeld H D 10 T

in extending the ordered ferromagnetic region above T

is shown together with the

corresponding B

that occurs when the ﬁeld is applied. From (8.22), it is seen that

B

reﬂects the change in E

hop

due to the applied ﬁeld that causes the magnetore-

sistance effect.

By combining (8.22)and(8.18), magnetoresistance curves can be computed

for any set of material parameters or external ﬁeld values. In Fig. 8.13,  vs. T

data [36] for a composition estimated as



0:77

0:23



MnO

subjected to H

ﬁeldsof0,1,3,5,and14Tareﬁttedbycurvesgeneratedfrom(8.19)incom-

bination with (8.22) using the above values for E

hop

and E

hop

, x D 0:23,and

C D 6 m cm .eV/

1

. Except for the H D 0 curve, which did not reach its full

peak probably due to the inhomogeneously broadened tail of the thermomagnetism

curve and the possibility that the specimen was not magnetically saturated, and the

one for 14 T, which may exceed the range of validity of the approximations, the-

ory and data are in reasonably good agreement. Because of the magnetocrystalline

Fig. 8.12 Calculated plots

and B

vs. T for

D 300 K with H D 0 and

10 T. Figure reprinted from

[35] with permission.



1996 by the American

Institute of Physics

8.3 Magnetoresistance in Oxides (CMR) 407

Fig. 8.13 Comparison of B

approximation theory with experiment for  vs. T with H D 0,1,3,

5, and 14 T. Data are from Li et al. [36]. Figure reprinted from [35] with permission.

 1996 by

the American Institute of Physics

anisotropy ﬁelds, which can probably reach beyond ﬁelds of 0.1 T, the presence of

domains of varying size and disposition should be expected at low ﬁelds and tem-

peratures approaching T

Part of the discrepancy between theory and experiment is the result of the molec-

ular ﬁeld approximation which represents the z-axis projection of the combined

magnetic moment from all of the spins that occupy a cone of average half angle

. Any difference between  and the average canting angle between neighboring

and S

spins could account for the relatively small disagreement between theory

and measurement in the metallic region below T

. It has also been assumed that the

polaron charges are randomly dispersed providing a net molecular ﬁeld coefﬁcient

that is constant with temperature when in fact it probably changes as the various ex-

change couplings compete for dominance as polaron charges shift about to maintain

the lowest lattice energy.

Another consideration is the role of the polaron bandwidth (or inverse lifetime)

which narrows with increasing temperature. As indicated by (8.16)and(8.17),

carrier transport is likely to be by tunneling at the lowest temperatures, but the co-

herence could dissipate and give way to random thermal hopping well before the

Curie temperature is reached. Since the Debye temperatures of these compounds

can be less than 200 K, the onset of nonadiabatic hopping could begin at temper-

atures below the liquid nitrogen range. This tunneling temperature regime would

fall into the range of HTS found in perovskite cuprate lattices. With an appropriate

value for b

, a more reﬁned model that includes the inﬂuence of quantum tunneling

as a function of magnetization could be constructed to calculate more accurately the

resistivity temperature dependence as the material evolves from metal to insulator

as T ! T

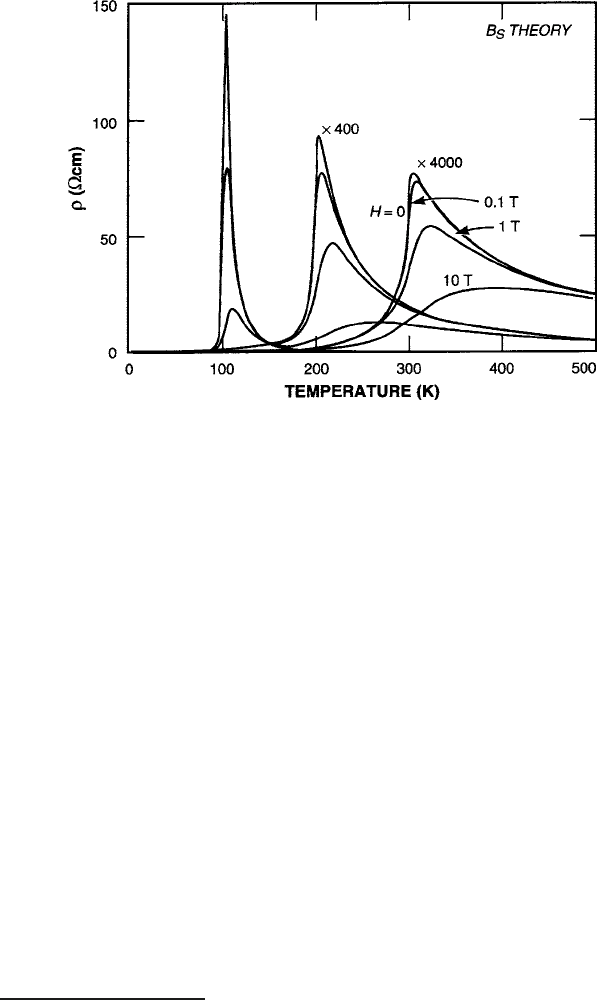
408 8 Spin Transport Properties

Fig. 8.14 Predicted plots of  vs. T by the B

approximation for T

values of 100, 200, and 300 K.

Magnetic ﬁeld strengths are H D 0, 0.1, 1, and 10 T. Figure reprinted from [35] with permission.

 1996 by the American Institute of Physics

In Fig.8.14, example curves of  from the B

approximation are plotted as func-

tions of T with H values of 0, 0.1, 1, and 10 T for Curie temperatures at 100, 200,

and 300 K. Since E

hop

is a constant of the transfer ions, the peaks of  at H D 0

should theoretically touch the insulator-phase envelope (given by a  calculation

using the full E

hop

 0:1 eV) at each of the T

values. From these results, the mag-

nitude of the anomalous increase in  at T

is shown to increase by almost four

orders of magnitude between 300 and 100 K.

Some conclusions can be drawn from this analysis (1) the metal–insulator transi-

tion occurs at the Curie temperature, which is an intrinsic property of the exchange

ﬁeld and therefore the chemical bonding of the material, (2) the metallic property

deﬁned by the positive slope of the  vs. T curve is the direct result of the negative

slope of the magnetization M vs. T curve, (3) the magnetoresistance is the result

of enhancement of the intrinsic exchange ﬁeld by an external magnetic ﬁeld, (4)

the magnitude of the external ﬁeld needed to cause signiﬁcant changes in resistiv-

ity must be on the same scale as the exchange ﬁeld, i.e., greater than 10 T, and (5)

the peak resistivity and magnitude of the magnetoresistance decrease with rising

temperatures.

Note that if the curves in these ﬁgures were extended to T D 0,  would begin to rise sharply

at T  40 K because of the elastic trap energy E

hop

D 4 meV. In reality, the thermal hopping

mechanism may be dominated by polaronic tunneling at these lowest temperatures and the metallic

region would theoretically reach T D 0,where would also approach some residual value.

8.3 Magnetoresistance in Oxides (CMR) 409

The model used above is derived from the notion that spin directions undergo

canting as the temperature increases. This is the Boltzmann statistical basis of the

Brillouin–Weiss theory that was applied in a direct fashion to the carrier trap en-

ergy which is allowed to vary as a continuous function of temperature and magnetic

ﬁeld. A more simpliﬁed view of the CMR effect could be constructed by treating

the carriers as comprising two groups, each with ﬁxed activation energies: those

free to be transported with minimum activation energy (E

hop

) permitted by ferro-

magnetic ordering and those from a paramagnetic phase with trap energy E

hop

from

(8.10). Partitioning of the carrier populations could be determined by separating

the magnetic components according to B

(for ferromagnetic spins) and (1  B

)

(for paramagnetic spins), each weighted by their respective activation probabilities

exp



E

hop

=kT



and exp



E

hop

=kT



. Such reasoning would lead to an alterna-

tive version of (8.18):

 D



eff





1

; (8.23)

where n

eff

D n

eff

exp



E

hop

=kT



C .1  B



E

hop

=kT



. By inspecting

(8.23), we see that  approaches (8.18) in the high temperature limit. In the regime

below T D T

,a vs. T curve can be constructed directly from Fig. 8.12.However,

this approach could be useful in the immediate vicinity of T

where the approxima-

tion of a two-phase magnetic system might reasonably represent the breaking down

of spin ordering. Where magnetic ordering is not a direct issue in determining the

degree of carrier availability, a model based on two distinct carrier trap energies can

also produce interesting results when applied to the case of HTS in Sect. 8.4.

At higher temperatures, changes in the cation charge distribution could enable the

rhombohedral (trigonal) phase to extend beyond x D 0:5, giving rise to the peculiar

antiferromagnetic/ferromagnetic transition ﬁrst reported by Jonker and Van Santen

[26]for



0:3

0:7



MnO

. In the regime where the ferromagnetic stabilization can

no longer dominate, a variety of antiferromagnetic ordering conﬁgurations can ap-

pear labeled as type A, C, and CE, where mixed Mn

and Mn

ions compete for

spin alignments, and G for the stable antiferromagnetic end member x D 1 with

only Mn

ions [37]. The phenomenon of magnetoresistance can still occur when a

large enough applied ﬁeld is able to upset the net exchange ﬁeld and reverse the sign

of the resultant J constant. Structural symmetries react to the magnetic and charge

order, as the relative disposition of the d

and d

y

orbitals continue to deter-

mine the nature of the spin ordering and the anisotropy of charge transfer, whether

along respective z-axis chains or within x–y planes. Detailed low-temperature phase

diagrams for the manganite systems that correlate magnetic, crystallographic, and

phases can be found in publications by Goodenough [37,38].

A comment on the conduction properties of the inverted spinel (generic formula





) magnetite Fe





is in order. Although metallic

conduction can be attributed to the polaronic charge transfer between octahedral

(B-site) Fe

–Fe

ions via the incoherent hopping mechanism Fe

$ Fe



, above the charge ordering Verwey temperature (120 K) where the trap energy

drops from 0.15 eV to 0.04–0.06 [39], there remains the large antiferromagnetic

410 8 Spin Transport Properties

contribution to the trap energy from the A sublattice. Moreover, the ferromagnetic

spin transfer is likely between only one of the ﬁve orbital states, which leaves the

remaining four to oppose it by correlation superexchange [40]. Recent analysis has

indicated that the overall exchange interaction between the B-site Fe ions remains

antiferromagnetic despite the signiﬁcant double exchange effect [41]. As a result,

the prospects of achieving a high degree of polarized spin transport in a true ferri-

magnet seem remote because of the frustration tendencies endemic to systems with

opposing sublattices. The relatively small E

hop

at room temperature, however, sup-

ports the suggestion that the value of U

eff

in the Sr





compound

is also small.

8.3.3 Dilute Magnetic Oxides

As a prelude to a discussion of large polaron superconductivity, some observa-

tions concerning polarized spin transport in magnetically dilute compounds are

appropriate. Following reports of parallel spin ordering above 300 K, magnetically

dilute oxides have been investigated vigorously in the search for room-temperature

magnetic semiconductors. Because the spins are isolated as ionic substitutions in

crystalline compounds, the apparent ferromagnetic effects that can exist to 1,000 K

are not explained by conventional orbital overlap exchange. For magnetically dense

ferrites with Curie temperatures (T

) that range from 500 to 900 K, even modest

dilution of the iron will sharply reduce T

to well below these levels, as explained

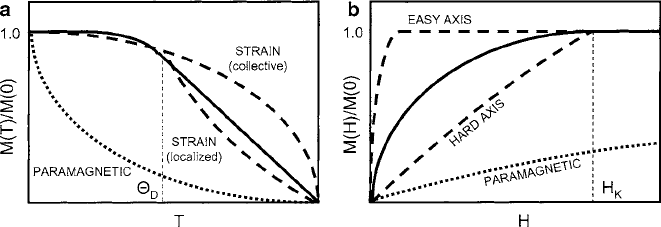
in Chap.4. Other features peculiar to these dilute magnetic systems are sketched in

Fig. 8.15. Measured thermomagnetism behavior in (a) generally follows a linear

Fig. 8.15 Schematic models of magnetization in dilute magnetic oxides: (a) comparison of pro-

posed thermomagnetic concave and convex contours for localized and cooperative magnetoelastic

extremes. The more linear intermediate curve suggests that magnetoelastic spin ordering (en-

hanced by ferromagnetic double exchange) percolates at lower concentrations than shorter-range

antiferromagnetic exchange. Because the static strain follows the Debye temperature 

, while

the important parameter of exchange is the Neel temperature, competition would be expected as

temperature and concentration increases. In part (b) corresponding magnetization curve models

showing the effect of collective magnetocrystalline anisotropy. The dashed curves represent the

condition where external uniaxial stress deﬁnes the limits of collective easy and hard magnetic

directions of the cooperative magnetostrictive strain

8.3 Magnetoresistance in Oxides (CMR) 411

slope (solid curve) rather than the familiar a Brillouin–Weiss convex contour,

suggesting the absence of a magnetic bias ﬁeld proportional to the magnetization,

i.e., a magnetic exchange ﬁeld H

D NM. Moreover, T

values vary little among

the different magnetic ion/oxide combinations, and are generally insensitive to the

magnetic ion concentration at low levels [42]. Magnetic saturation in (b) usually re-

quires several kOe of ﬁeld, indicating a signiﬁcant anisotropic demagnetizing ﬁeld.

Vanishingly small remanent moments suggest signiﬁcant stress demagnetization,

thereby indicating further the presence of magnetoelastic ions [43].

Two properties of these compounds have attracted the attention of researchers:

(1) the magnetic impurity concentration should be low enough .<10%/ to avoid the

occurrence of local antiferromagnetic pairs and (2) for good electrical conduction,

the impurity concentration must include mixed-valence states and be high enough

to produce charge transfer via polarons with aligned spins. This latter issue remains

a subject of concern, however. Because of the low densities of magnetic ions, argu-

ments that the reported ferromagnetic spin ordering is the result of itinerant spins

stabilized in antibonding states by conventional exchange are difﬁcult to support

on theoretical grounds. Without an aligning ﬁeld of many Tesla, the dilution of the

magnetic system will have the magnetization of a simple paramagnet that will not

survive to temperatures much above the cryogenic range.

From the discussion of exchange ﬁeld effects on the intensity of microwave mag-

netic resonance in Sect. 7.1, it was concluded that when a population of independent

spins become stabilized into a collective magnetic moment m, the distribution of the

population among available states as a function of temperature will not follow the

Boltzmann partition theory unless the effective temperature of the spin system is

reduced according to the strength of the alignment interaction [44]. Instead of the

scalar addition of a Weiss molecular (exchange) ﬁeld exponent m.H

C H/=kT

that serves to explain the coexistence of microwave (Zeeman effect) and infrared

(exchange) resonances discussed, the higher energy stabilization of the magnetic

system might also be created by a cooperative magnetoelastic effect induced by a

polarizing magnetic ﬁeld or uniaxial (or planar) stress “ﬁeld” sufﬁcient to percolate

local site distortions into a net strain, e.g., with Mn

J–T ions in Y

[59 of

Chap. 5, 45]. Such an energy condensation would be the result of an incipient mag-

netostrictive strain that overcomes local constraints imposed by the undistorted host

sites. The lattice would then respond to an aligning magnetic or strain bias ﬁeld that

encourages the formation of a cooperative magnetoelastic ground state of energy

approaching that of the combined unrestrained J–T stabilizations [46].

If a magnetoelastic energy term E

is included, (7.9) can be expressed as



C E



(8.24)

and the Brillouin function becomes B.T / D tanh .E

=2kT

/. The internal polar-

izing ﬁeld term E



1 cm

1



is linearly dependent on the spin alignment, while

the spontaneous exchange term E



500 cm

1



has a quadratic dependence on

spin ordering. Note that E

can also represent an anisotropy ﬁeld arising from