Dionne G.F. Magnetic Oxides
Подождите немного. Документ загружается.

432 8 Spin Transport Properties
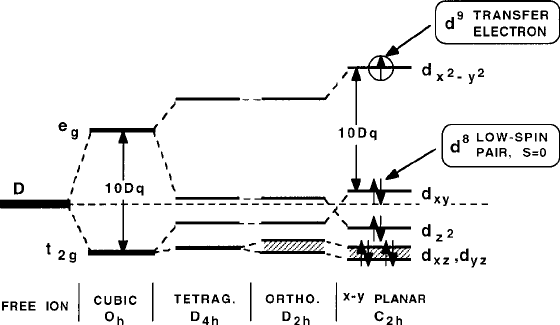
Fig. 8.30 Crystal-field diagram illustrating the d
8
low-spin
.
S D 0
/
state with the free ion level
as zero-energy reference [9]
the antibonding e
g
–p¢ orbital states are split into lower d
z
2
and upper d
x
2
y
2
,
where the unpaired spin is located and from which the polaronic transfer of spins
to neighboring ions will take place. Note that the t
2g
states remain labeled as non-
bonding because of their weak overlaps with the oxygen 2p lobes. With reference
to Fig. 8.18, the Cu sites of the superconducting perovskites are either tetragonal
(with an orthorhombic component in some cases), pyramidal, or square planar. The
relevant spin occupancies of the d states are now shown in Fig. 8.30. With d
x
2
y
2
as the path of transfer, with single occupancy in the Cu
2C
d
9
member and empty
for the Cu
3C
d
8
member in a low-spin .S D 0/ state, as illustrated in Fig. 8.31
and earlier as part of Fig. 8.9.
The source of polarons differs among these compounds. In the simplest case
of the La
3C
2x
Sr
2C
x
Cu
2C
1x
Cu
3C
x
O
4
system with maximum T
c
40 K[50], Sr
2C
ions are fixed negative charges in the A sublattice, and the mixed valence occurs
as tetragonally coordinated Cu
3C
holes that are tethered to the nearest Sr
2C
ions,
thus making the conductivity p-type. A modification of this system that introduces
the pyramidal coordinations La
3C
2x
Sr
2C
x
Ca
Cu
2C
1x
Cu
3C
x
2
O
4
increased T
c
to 60 K
[77]. For the YBa
2
Cu
3
O
y
system with T
c
95 K[51], the situation is more com-
plex. The mixed valence occurs here as a result of oxygen vacancies which establish
polarons in both the planes of Cu .2/ –O
5
pyramids and Cu .1/ –O
2
linear chains;
chemical formulae highlighting proposed Cu valence distributions that vary linearly
with polaron concentration may be written as follows:
YBa
2
h
Cu
2C
5=2y=4
Cu
3C
y=43=2
i
2
h
Cu
2C
113y=2
Cu
3C
3y=210
i
O
y
for
6:67 y 7
and YBa
2
h
Cu
2C
5=2y=4
Cu
3C
y=43=2
i
2
h
Cu
1C
103y=2
Cu
2C
3y=29
i
O
y
,for
6 y 6:67,
with Cu(1) and Cu(2) site valences v .1/ D 1:5y 8 and v .2/ D 0:25y C 0:5,
respectively.

8.4 Superconductivity in Oxides 433
Fig. 8.31 p-Type 3d
x
2
y
2
2p
y
Cu
2C
O Cu
3C
covalent transfer in 180
ı
perovskite bond
geometry for d
9
! d
8
(low-spin) [9]
As suggested by Fig. 8.32, the superconduction is likely to occur in the
Cu .2/ –O
4
planes of the pyramidal complex, because the Cu
2C.3C/
content of
the Cu .1/ –O
4
planes would phase over to Cu
1C.2C/
at y D6:67 as a result of
oxygen vacancies within the plane that create the Cu .1/ –O
2
chains. Moreover,
these vacancies would break up the continuity of the transfer couplings neces-
sary for superconduction. The origin of positive mobile polarons, therefore, would
arise from the fixed negative charges of O
2
ions filling the vacancies, as y ! 7.
In Sr-free La
2
CuO
4Cı
[78], the excess oxygen is more correctly described by
La
2x
Cu
2C
1x
Cu
3C
x
O
4
, which is brought about by La cation deficiencies. As de-
termined earlier, a threshold value of x
0
0:08 (or ıD0:04) is all that is necessary
for the onset of superconduction.
Partial verification of this valence model was reported by Tranquada et al. [60]
who determined experimentally that the average spin of the Cu(2) ions is 0.66 Bohr
magnetons .m
B
/ at y D 6, and that the Cu(1) sublattice is diamagnetic. This result
indicates that most of the Cu(2) ions are 2C (with some spin canting likely reducing
the effective spin values) and that the Cu(1) ions are 1C, which is consistent with the
model in Fig. 8.33. The occurrence of Cu
1C
ions in the Cu .1/ –O
2
chains should be
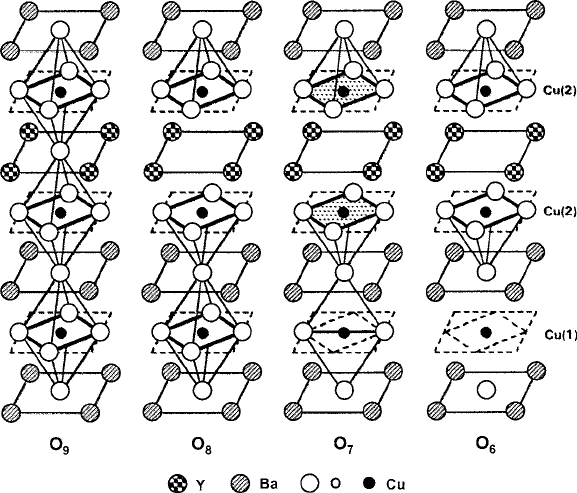
434 8 Spin Transport Properties
Fig. 8.32 Ordered A-layer structure of YBa
2
Cu
3
O
y
, showing breakdown of Cu–O
6
complexes as
y decreases from 9 (hypothetical in this case). At y D 8, oxygen is removed from Y–O
4
planes and
Cu(2) sites are square-pyramids (i.e., Cu–O
5
), but retain C
4
symmetry axis. At y D 7, Cu(1) ions
become linearly coordinated in x–y plane (orthorhombic phase), with uniaxial superconduction
expected; Cu(2) ions retain square-planar coordination in x–y plane, with planar superconduction
possible. At y D 6, Cu(1) planes are fully depleted of oxygen and Cu(2) ions lose mixed-valence
with only 2C species present (see Fig. 8.33)[9]
expected, since its large radius
0:96
˚
A
would preclude its occupancy of the Cu(2)
pyramidal sites; furthermore, there is already ample evidence for d
10
configurations
to favor linear coordinations [79].
An even more intriguing confirmation of this originally proposed linear Cu va-
lence distribution has come from the “bond valence sum” analysis of Brown [80].
The results plotted in Fig. 8.34 indicate that the Cu valence distribution is basically
linear, but with an oscillation about the relevant portion of the linear curve from
Fig. 8.33, added here for comparison.
Together with the compounds discussed above, the parameters for more-
complicated “layered” structures are summarized in Table 8.1. In cases where
the Cu resides principally in sites with O
4
coordinations, which may provide
E
hop
>4meV, T
c
can reach 120 K. For the Bi
3C
2
Sr
2C
; Ca
2C
3
Cu
2C.3C/
2
O
8Cı
system [63], the optimum Cu
3C
concentration xD0:33 occurs because of a com-
bination of excess O
2
(i.e., ı 0:17) or the occurrence of monovalent calcium
[81]. The Tl
3C
2
Ba
2C
2
Ca
2C
x1
Cu
2C.3C/
x
O
4C2xCı
compounds [82] derive their po-
laron sources from either fixed-valence cation deficiencies (i.e., excess O
2
)orthe
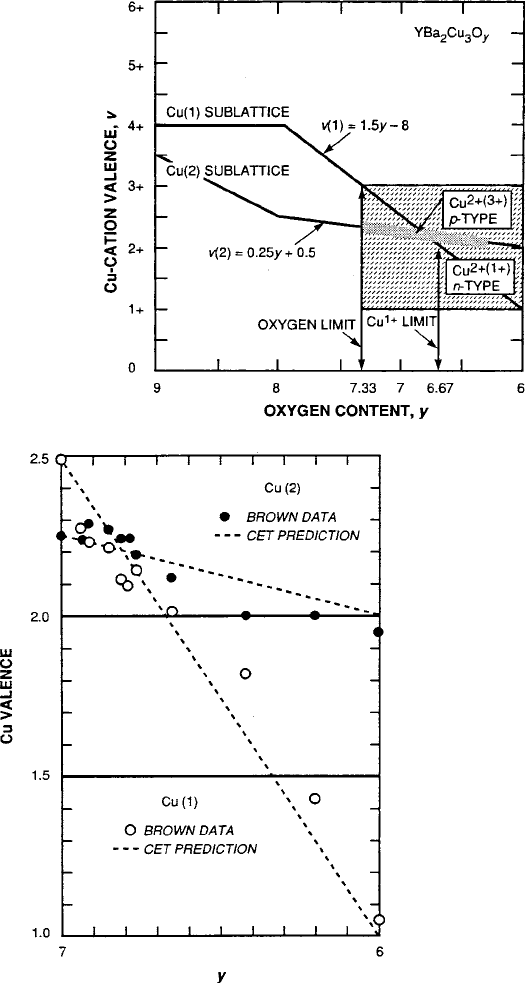
8.4 Superconductivity in Oxides 435
Fig. 8.33 Proposed linear
valence model of Cu(1) and
Cu(2) as a function of the
oxygen content variation and
distribution depicted in
Fig. 8.32 [9]
Fig. 8.34 Nominal Cu valence as determined from linear model of Fig. 8.33 compared with
valence-bond-sum analysis of Brown [80]forYBa
2
Cu
3
O
y
[9]

436 8 Spin Transport Properties
Table 8.1 Layered cuprate superconductors
a
E
hop
b
Compound O
2
coord. T
c
(K) x (meV) ˇ
b
Ref.
p-type
Cu
3C
C
La
2x
Sr
x
CuO
4
Cubic O
6
40 0.2 2.5 0.7 [50]
La
2x
Sr
x
CaCu
2
O
4
Pyramidal O
5
60 0.2 4 0.7 [77]
YBa
2
Cu
3
O
y
Pyramidal O
5
95 0.25 4 0.57 [51]
Bi
2
.
Sr; Ca
/
3
Cu
2
O
8Cı
Planar O
4
120 0.33 (>4)(<0:5)[63]
Tl
2
Ba
2
CuO
6Cı
Cubic O
6
80 – (2.5) (<0:5)[82]
Tl
2
Ba
2
CaCu
2
O
8Cı
Pyramidal O
5
110 – (4) (<0:5)[82]
Tl
2
Ba
2
CaCu
2
O
10Cı
Planar O
4
120 – (>4)(<0:5)[82]
Hg
2
Sr
2
Ca
n1
Cu
n
O
2nC4Cı
Pyramidal O
5
135 – (>4)(<0:5)[112]
c
n-type
Cu
1C
Nd
2x
Ce
x
CuO
y
Cubic O
6
24 0.23 (2.5) (>0:7)[83]
Sr
1x
Nd
x
CuO
2
Planar O
4
40 0.14 (4) (>0:7)[85]
a
Some entries of this table are taken from Table 8.1 of reference [86]
b
Brackets indicate suggested values
c
This compound was prepared under high pressure which, together with Hg, probably increased
the covalent exchange energy b
p
between the Cu ions
mixed valence of Tl, which can appear as 1C or 3C to suit the ionic size or charge
requirements of its locale. With such a dual mixed-valence condition present, the
likelihood of higher polaron ordering, i.e., smaller ˇ, is also increased. Since any
defects would not be oxygen, these compounds should have chemical stability that
is superior to the YBa
2
Cu
3
O
y
system.
Another source of the enhanced T
c
values could be larger b values that result
from a covalent coupling between the d
x
2
y
2
–2p¢ antibonding state and the 6s
orbital of Bi
3C
or Tl
1C
. An increased exchange integral would give rise to a smaller
x
t
. A measurement of the W parameter for the compositions with maximum T
c
could help to sort out these possibilities.
Zero-spin polarons can also occur in cuprates with n-type conduction prop-
erties. In A
2
BO
4
perovskites, Cu
1C
–O
2
–Cu
2C
combinations can produce su-
perconductivity with Cu
1C
d
10
;S D 0
ions as the minority carrier instead of
Cu
3C
d
8
;S D 0
. Through Ce
4C
substitutions in A sites and the creation of O
2
vacancies by a reducing atmosphere anneal, Tokura et al. [83] reported n-type su-
perconductivity with T
c
24 KinNd
3C
2x
Ce
4C
x
Cu
2C
1x2y
Cu
1C
xC2y
O
4y
,for
z D 0:15 and y D 0:04. As a consequence, stoichiometry is maintained with a
Cu
1C
concentration of x D 0:23.
Although the critical temperatures of this system are not particularly large,
14
these results are very significant for providing insight about the microscopic
mechanism of superconductivity. The substitution of tetravalent cations into the
14
Since Nd
3C
is a magnetic rare-earth ion with S D 3=2, superexchange involving the A sublattice
may result in Ce
4C
clustering that would lead to larger ˇ parameters.
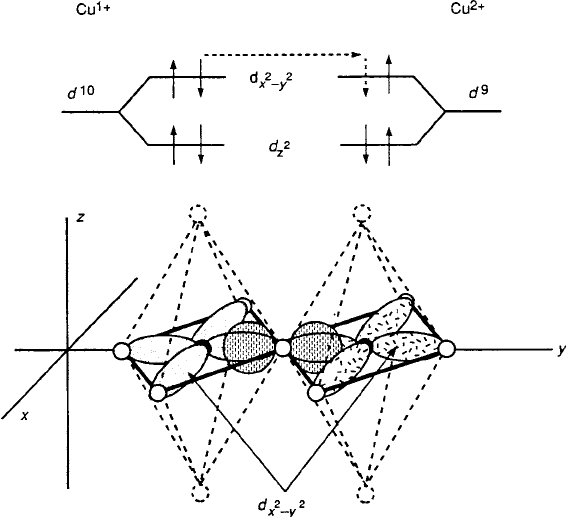
8.4 Superconductivity in Oxides 437
Fig. 8.35 n-Type 3d
x
2
y
2
2p
y
Cu
1C
O Cu
2C
covalent transfer in 180
ı
perovskite bond
geometry for d
10
! d
9
[9]
A sublattice creates negative polarons (electrons), and the appearance of super-
conduction verifies the prediction of n-type Cu
1C
! Cu
2C
C e
orbital transfer
predicted in the initial report on the CET model [84]. As shown in the orbital trans-
fer diagram of Fig. 8.35,thed
x
2
y
2
orbital is again the transfer path. Here the Cu
1C
ions provide the S D 0 states required for spin transfer and the onset on magnetic
frustration in the Cu
2C
host lattice with S
L
D 1=2. In addition, the existence of
n-type superconduction significantly weakens the argument that high-T
c
phenom-
ena are based on hole transport through the oxygen sublattice, i.e., local peroxide
O
1
formation. For the oxygen ligands to provide conduits for electrons, O
3
ions
would have to be postulated – a situation even more unlikely than the peroxide case.
Another interesting feature of these compounds is the necessity to create oxygen
defects as part of their preparation. In this case, the Cu
1C
ions occupy square pla-
nar sites .Cu–O
4
/, with an occasional missing oxygen, As shown in Fig. 8.32 for
YBa
2
Cu
3
O
y
, the Cu(1) sites that are proposed to harbor Cu
1C
ions are also square
planar to linear, as y falls below 7. Since Cu
1C
ions are usually not accepted in sites
of higher coordination, e.g., octahedral O
6
, because of their large radii
0:96
˚
A
,
this result is entirely consistent with traditional metal-oxide chemistry.
A primitive layered n-type family Sr
2C
1x
Nd
3C
x
Cu
2C
1x
Cu
1C
x
O
2
was reported by
Smith et al. [85]. In this case, the Cu ions reside in planar coordinations, with the A
438 8 Spin Transport Properties
sites forming oxygen-free layers that are interleaved between Cu–O
4
planes. The n-
type compositions are noteworthy because of the increased T
c
D 40 Kandthelower
value of x
max
D 0:14. In the context of the foregoing discussion, these results may
be explained by an E
hop
higher than that of the compound containing Ce
4C
, but with
alargerˇ parameter, as compared in Table 8.1. This interpretation remains in accord
with the general conclusions that T
c
through E
hop
has a crystal-field dependence re-
lated to oxygen coordination, and that cation spatial ordering is essential for high T
c
.
Mixed-valence combinations involving zero-spin transition ions were examined
further in the context of HTS materials design [86]. Figure 8.21 suggests how var-
ious zero-spin polaron possibilities could be developed from low-spin states to
participate in coherent spin tunneling. In certain lattice structures, the t
2g
shell can
be the source of superconductivity, as confirmed by the critical temperature of 4.7K
reported for low-spin Co
3C
d
6
;S D 0
and Co
4C
d
5
;S D 1=2
combinations in
Na
1C
x
Co
3C
x
Co
4C
1x
O
2
that becomes n-type when hydrated, with likely composition
Na
1C
0:35
Co
3C
0:35
Co
4C
0:65
O
2
1:3H
2
O[87].
Because these situations require strong cation–anion interactions, the possibility
of utilizing cations with the longer reaching radial components of the 4d
n
and 5d
n
shells might be attractive candidates for future investigation. Larger U
p
values to-
gether with greater and b
p
integrals could result in increased T
c
values through
favorable E
hop
=W ratios in (8.39). Low-spin combinations of the strongly covalent
Ru
2C
4d
6
;S D 0
and Ru
3C
4d
5
;S D 1=2
ions in highly reduced stoichiom-
etry, for example, would satisfy the U
ex
D 0 condition that allows b
2
p
U
2
p
,
and charge ordering could then parameter optimize the polaron dispersal for spin
transport. In the octahedral sites of a spinel lattice, a T
c
12 K derived from t
2g
shell d
xy
–d
xy
¢ delocalization exchange
3d
1
$ 3d
0
was observed from n-type
Ti
3C
! Ti
4C
C e
transfers [88].
In summation, the mixed-valence manganites and cuprates are metallic if the po-
laron trap energy from antiferromagnetic exchange is eliminated. La
1x
Ca
x
MnO
3
is metallic for x<0:5because of the occurrence of ferromagnetism that results
from vibronic Jahn–Teller effects and delocalization exchange between partially
filled e
g
orbital states. Above x D 0:5, the crystallographic structures are influenced
by a complexity of factors that include J–T distortions that in turn control the split-
ting of the e
g
states. Magnetic order can then be established in a variety of antifer-
romagnetic configurations, often tenuous and subject to insulator–metal transitions
when high magnetic fields reverse the sign of the resultant exchange field to restore
the ferromagnetism and create and produce a significant magnetoresistance effect.
An internal spontaneous magnetic moment acting as a magnetic source, however,
would oppose the flux exclusion (Meissner effect) that is a fundamental property of
superconductivity. p-Type La
3C
2x
Sr
2C
x
Cu
2C.3C/
O
4
is metallic because zero-spin
Cu
3C
“hole” carriers (or Cu
1C
carriers in n-type La
3C
2x
Ce
4C
x
Cu
2C.1C/
O
4
) can
transport as large polarons in the charge-ordered B sublattice. These conditions
remove the possibility of magnetic exchange trapping and frustrate any antifer-
romagnetic order above a concentration threshold of only a few percent. In both
materials systems, large polarons can become itinerant, in one case contributing to a
8.5 Supercurrents and Magnetic Fields 439
condition from which a magnetoresistance anomaly may occur at the Curie temper-
ature, and in the other, making possible the coherent transfer among S D 1=2 and
S D 0 charge-ordered and spin-frustrated ions that is necessary for a superconduct-
ing state. Other compounds where the absence of a magnetic exchange trap allows
polaronic conductivity to condense into superconductivity are the mixed-valence
Ti, V, and Bi oxides [89].
8.5 Supercurrents and Magnetic Fields
From this model, two-fluid functions can be developed to analyze penetration
depths, critical magnetic fields, critical current densities, and other properties as a
function of temperature [23]. The end result in each case is determined by the super-
carrier density n
s
. One central result of this approach to the superconducting state
that arises from the Boltzmann-type partitioning of the carriers, however, is that the
supercarrier population will decrease accordingly with temperature until the density
of supercarriers falls below the threshold value of n
t
and the superconducting state
is extinguished. As a consequence, high supercurrent densities would be expected
only at the lower temperatures regardless of the critical temperature value.
Although the basic requirement for zero resistance has been defined as n
s
n
t
,
this condition alone is not sufficient for superconduction. Superconductivity is a
thermodynamic state of energy lower than the normal state, and condensation to
the superconducting state occurs when this stabilization energy is transferred to a
supercurrent flow. In the following sections, the role of magnetic field in limiting this
current is described, and the factors that determine critical magnetic field, critical
current density, and related phenomena are examined [9].
8.5.1 Supercurrent Formation
It is important to remember that a superconductor is not a “perfect” conductor.
Perfect conduction implies simply zero electrical resistivity – the unrealizable case
of universally unimpeded charge transport. For a material to be a perfect conductor,
there can be neither scattering among carriers nor energy loss in the form of thermal
dissipation through electron–phonon interaction. In reality, electrons in a solid can
never be completely uncoupled from the lattice, and where so-called “free” electrons
are involved, the state occupation limitations imposed by the Pauli exclusion princi-
ple create a repulsive action that also limits current flow. Superconduction, however,
requires spatial rigidity of the supercurrent in order to fulfill the E D 0; B D 0 con-
ditions. As pointed out in the discussion of (8.26), supercurrent rigidity .ri
s
D 0/
requires both rA D 0 (the London gauge) and rn
s
D 0, where the latter is
also a sufficient condition that implies real-space ordering of supercurrent carriers
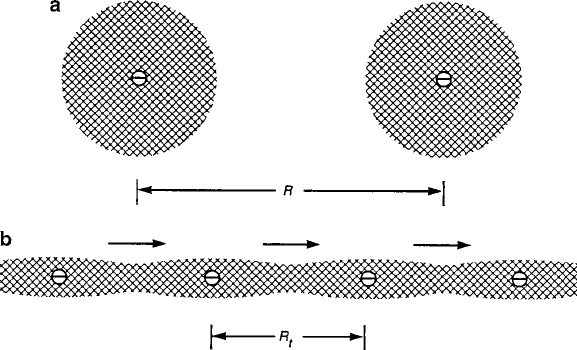
440 8 Spin Transport Properties
Fig. 8.36 Two-dimensional model of polaron condensation to superconducting state: (a)be-
low percolation threshold and (b) after ferroelectric alignment with ordered supercurrent flow
at R D R
t
[9]
that may also involve some form of dynamic spin ordering. The spatial ordering of
charges .rn
s
! 0/ suggests a MO scheme as a source of rigid conduits for super-
current flow.
If mixed valence can provide conduction among bonding electrons delocalized
within the directed lobes of their covalent bonds, electrostatic ordering of these car-
riers must exist; lattice periodicity alone would suggest a regularity for any carriers
participating in the bonding. The charge balance requirements for optimizing the
Madelung energy also dictate such a spatial distribution of valence states. Since part
of the trapping or stabilization energy of the carrier is due to the electrostatic attrac-
tion to its polaron source, i.e., the other half of its electric dipole, the carrier ordering
is dictated by the dispersal of the fixed polaron sources, as depicted in Fig. 8.36a. For
vanishingly small concentrations, the carriers are isolated, with radially symmetric
cell profiles in an x–y plane (in reality, only the fourfold symmetry of a d
x2y2
orbital in the CuO
4
square-planar case). As the spatial density of polaron “cells”
increases, the shapes of the overlapping regions converge into a chain to assume the
minimum energy orientation of aligned electric dipoles. At a threshold density of
fixed polaron sources, condensation of ordered chains would occur spontaneously
in a manner depicted by Fig. 8.36b.
In the preceding sections, the necessary condition that D 0 was discussed
in terms of a series of parallel, independent chains that could be represented by
a one-dimensional model, since only one completed chain would be required for
zero resistance. For phenomena related to the buildup of supercurrent and its as-
sociated magnetic effects, however, orbital transfer can no longer be treated as an
isolated linear chain, but rather as series of interconnected chains distributed across
a macroscopic area.
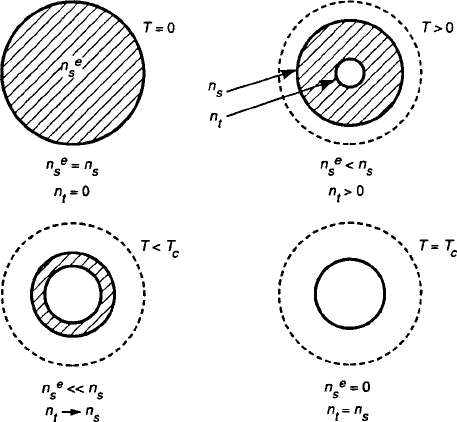
8.5 Supercurrents and Magnetic Fields 441
The completion of a single path is contingent on a threshold supercarrier density
n
t
, occurring at T D T
c
. Since a fraction of the electrons is in thermal activation at
all times, the total n
t
cannot be expected to complete every possible superconduc-
tion linkage simultaneously. Even if the chemical ordering were ideal .P D 1/,the
incidence of electron–phonon encounters is still random. An analog to this effect
would be the electrical breakdown of a gaseous medium, which begins with a single
irregular striation that moves about as dictated by random molecular collisions. As
the ionizing collisions increase with density, multiple striations percolate and the
gas is eventually transformed into a plasma continuum with a large fraction of the
ionized gas participating in the current.
At this point, we may reasonably assume that the current increases continuously
from zero, with only the excess of n
s
over n
t
initially contributing to the super-
current. An effective carrier density at T D T
c
is therefore defined as n
e
s
.T
c
/ D
n
s
.T
c
/ n
t
.T
c
/ D 0.AtT D 0, however, there are no hopping electrons and we
must assume that all of n
t
is contributing to the supercurrent, i.e., n
e
s
.0/ D n
s
.0/.To
satisfy these boundary conditions in the most direct manner, the above relation may
be generalized to all temperatures, according to
n
e
s
.T / D n
s
.T / n
t
.T /; (8.40)
where n
t
.T / D n
t
.T
c
/
1 n
e
s
.T / = n
e
s
.0/
Thus, the fractional contribution of the
threshold carrier density n
t
.T
c
/ to the supercurrent increases in direct proportion
to the buildup of the effective carrier density n
e
s
.T / as T ! 0. The logic of
(8.40) is displayed in Fig. 8.37,wherethen
e
s
.T / population declines because of the
Fig. 8.37 Pictorial representation of the simultaneous decrease of n
e
s
.T / and the growth of
n
t
.T / as T ! T
c
,wheren
s
and n
t
converge to establish the threshold density for the onset of
superconductivity [9]
