Dionne G.F. Magnetic Oxides

Подождите немного. Документ загружается.

422 8 Spin Transport Properties

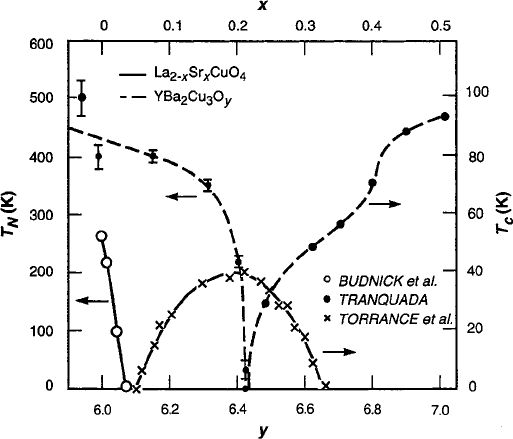
Fig. 8.20 Experimental veriﬁcation of the magnetic frustration requirement prior to the onset of

superconductivity in La

2x

CuO

and YBa

systems. Data from Budnick et al. [59],

Tranquada [60], and Torrance et al. [61]

ﬁxed negative charge represented by the Sr

dopant by establishing a ring of mo-

bile carriers (as in Fig. 8.2), and then to frustrate through spin canting the regions

beyond these lowest energy polaron sites. Where the charge transfer condenses into

a superconducting state at critical temperature T

, the threshold for frustration could

be reduced further. Experimental evidence of this condition is shown in Fig. 8.20

for two common cuprate superconductors [59–61]. Other possible S D 0 can-

didates among the 3d

series with occupied transfer orbitals d

y

and d

are

diagrammed schematically in Fig. 8.21.

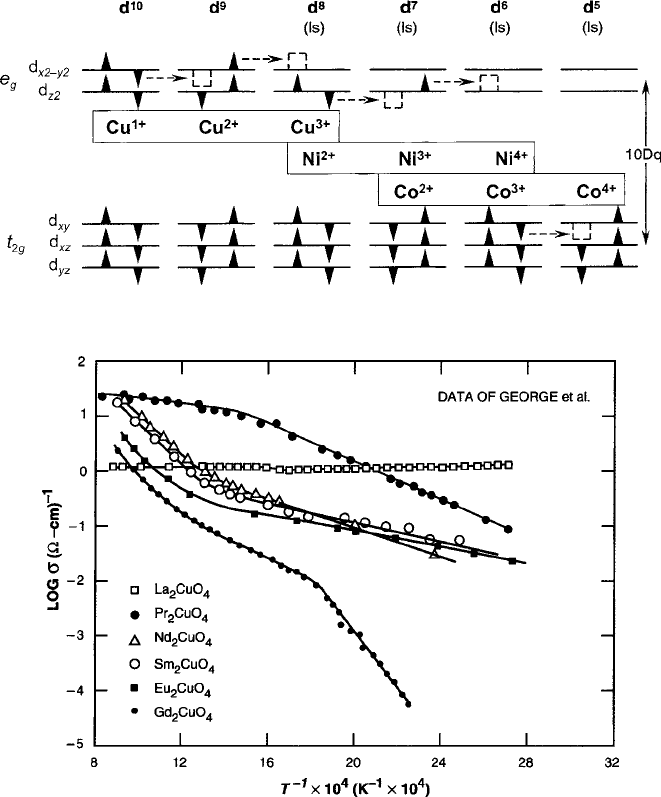
The inﬂuence of magnetic exchange on the Cu

–Cu

conductivity in the pres-

ence of rare-earth ions occupying the A sites is shown dramatically in Fig. 8.22,

where the data of George et al. [62] indicate the absence of activation energy for the

nonmagnetic La compound. In all of the others, antiferromagnetic interactions de-

ter the formation of large polarons that are necessary for the coherent activationless

charge transfer of superconductivity. As shown in Fig. 8.20, only about 5% zero-

spin Cu

could be sufﬁcient to frustrate the long-range antiferromagnetic ordering

in La

2x

CuO

and create the metallic phase that allows the onset of supercon-

ductivity (the T

, T

D 0 condition). When one considers that less than one-third

of the copper cations supply charge carriers, it would not be surprising to ﬁnd the

superconducting state to consist of spontaneously organized domains of metallic

diamagnetism interspersed with regions of insulating or semiconducting antiferro-

magnetism. Such a result is not unlike the room temperature formation of metallic

and insulator regions in the manganites [33].

8.4 Superconductivity in Oxides 423

Fig. 8.21 Schematic diagrams of S D 1=2 ! S D 0 transfers among 3d

ions in low-spin states

Fig. 8.22 Conductivity  data as a function of temperature, showing the inﬂuence on the activation

energies from RE ion exchange interactions with Cu

ions in a

CuO

series. Note the

absence of E

hop

in the La

CuO

case. Data are from George et al. [62]

8.4.3 Large-Polaron Superconductivity

Metallic conduction properties in oxides have been demonstrated to condense into

superconductivity at temperatures far above those of conventional metal and in-

termetallic compounds, reaching above 130 K [50, 51, 63]. To understand how

covalent tunneling in the form of large polarons can be the agent of HTS, the

424 8 Spin Transport Properties

nature of isolated larger polarons in diamagnetic or magnetically frustrated lattices

in the context of superconductivity phenomenology is considered. As introduced in

Sect. 8.4.1, the primary condition that evolves from the London equations when ap-

plied to a system of supercarriers of volume density n

in the real-space ideal case,

supercarriers must be spatially ordered, thereby rendering their transport coherent,

i.e., rn

D 0.

In collective-electron systems this spatial order condition can be treated by the

ensemble wave function

with spatial decay (coherence) length  according to the

proposed

exp .r=/. Because n

is represented by the quantum mechan-

ical probability density j

, the gradient expressed from (8.32) can be repeated as

.r/

D



exp









(8.33)





: (8.34)

If  !1, the London rn

D 0 requirement is satisﬁed. The magnitude of the

coherence length serves as a measure of the purity of the superconducting state

[54,64].

For the polaron case, the equivalent of j

would be the transfer efﬁciency .r/

of (8.14), which regrettably cannot be expressed as an exponential function in this

model because of the central electrostatic ﬁeld of the polaron trap given by (8.15).

To extend the comparison to (8.33), the notion of coherence would be deﬁned by

the stabilization energy of the covalent bond according to

r.r/



1 



D

Kab





: (8.35)

Since the bracketed .a=r/

is dimensionless, a characteristic dimension for an indi-

vidual polaron can be deﬁned as

D a



Kab



; (8.36)

which is the same as the result for the large polaron radius derived by Holstein [6],

except for a numerical multiplication factor. Consequently, the use of the polaron

radius as a measure of coherence of the superconducting state can be adopted with

the restriction that polaron dispersal must be achieved by real-space positioning of

the polaron sources. This limitation does not exist with collective electron super-

conductivity formalized in momentum–space.

Within an individual polaron cell, the carrier ranges spontaneously and coher-

ently through correlated transfers to a boundary deﬁned by the covalent strength of

the orbital bonds in which it resides and the polarizability of the lattice. In terms

of (8.36), the “quality” of the superconductor, i.e., r

instead of  in this model, is

determined by the product of the dielectric constant K and the exchange integral b

8.4 Superconductivity in Oxides 425

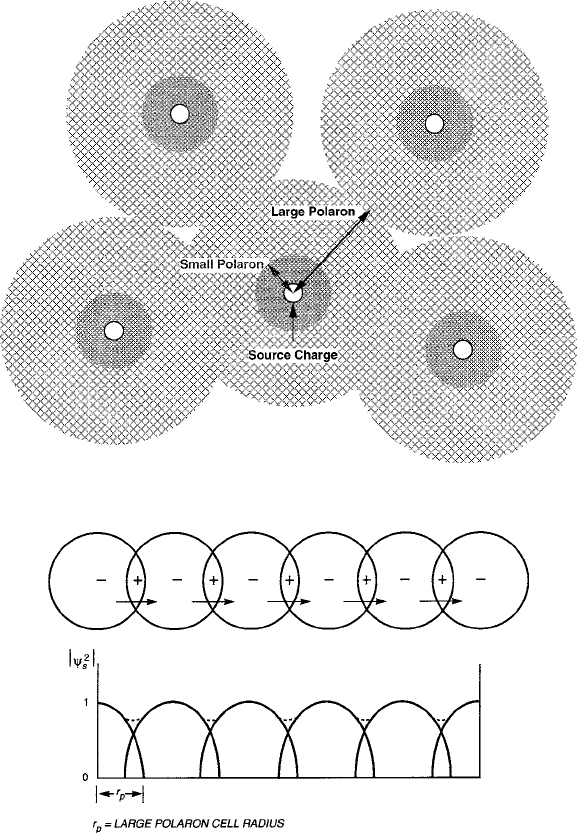
Fig. 8.23 Two-dimensional picture of large polaron cells amidst ﬁxed polaron ionic sources

Fig. 8.24 One-dimensional model of a large polaron chain, indicating the merger of carrier density

functions j

to establish a continuous molecular-orbital state

When the concentration reaches a percolation threshold where cells begin to over-

lap, the dispersed polaron carriers and their ﬁxed source ions sketched in Fig. 8.23

condense into a string or chain of dipoles and a dynamic ferroelectric state of coher-

ently tunneling carriers can form as in Fig. 8.24, still with one carrier per polaron

cell. The smallest concentration threshold would then be determined by r

, subject

to the attendant requirement that antiferromagnetic frustration must also occur.

426 8 Spin Transport Properties

Following the concepts of local vs. collective charge transfer, coherent tunneling

would survive only under the conditions (1) that polaron cell overlap be small

enough that Pauli scattering would be moot and Fermi statistics not be a concern

and (2) that thermal energy would not produce random hopping events to disrupt

the correlated charge ﬂow in the superconducting chains. The ﬁrst condition would

be concentration dependent, whereby the orbital levels would merge into a partially

ﬁlled band at high concentrations, producing normal metallic properties typical of

the t

-band metals such as CrO

mentioned in Sect. 8.2. A second limitation, which

is reﬂected in Holstein’s conclusion that hopping would dominate over tunneling

where T>

=2, could show its effect at even lower temperatures because of the

added requirement that the coherent chains of polaron carriers be continuous.

8.4.4 Normal Resistivity and Critical Temperature

From the above qualitative concepts, a “two-ﬂuid” model can be constructed to ac-

count for the resistivity characteristics of the HTS cuprate superconductors. This

can be accomplished in a straightforward manner; the total carrier concentration x

is divided into normal and superconducting fractions by means of the thermal acti-

vation probability function. The basic premise of this theory based on large polarons

is that carriers that are not activated by random lattice vibrations can be transported

through the bonding, and the formation of a coherent tunneling state among this

portion of the polaron population can then be established.

To begin the analysis, we deﬁne the normal carrier concentration as

D x exp





hop



; (8.37)

where E

hop

is the basic polaron trap energy that was deﬁned previously as E

hop

our discussion of the manganites. As an example of the normal resistivity behav-

ior of polaronic oxide compounds, (8.34) can be introduced to (8.19) to compute

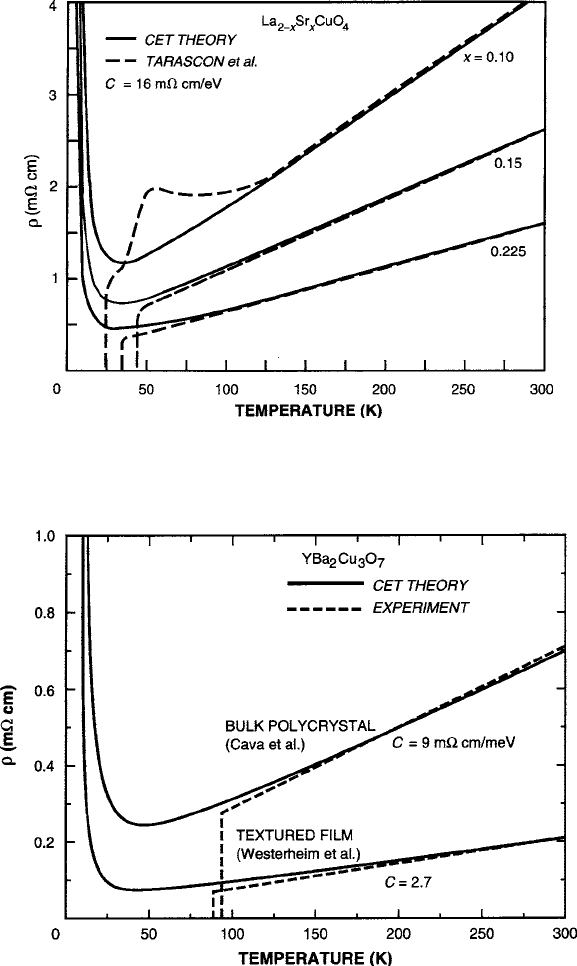
 vs. T curves similar to the model of Fig. 8.8. Above the critical temperature T

the resistivity behavior of La

2x

CuO

superconductors is metallic, as plotted in

Fig. 8.25. For the ﬁtting of these data [65] C D 16 m cm eV

1

, larger than that

for La

1x

MnO

partly because of 50% higher lattice volume fraction occupied

by octahedral B sites and the large angle grain boundaries in these bulk ceramic

specimens. In these calculations E

hop

D 4 meV for each value of x D 0:10, 0.15,

and 0.225. Note that the onset of superconductivity occurs at the resistivity mini-

mum, which suggests that the polaron trap could be the key to determine the value

of the critical temperature. A second comparison between theory and experiment

[66] is presented in Fig. 8.26 for data from the most commonly studied compound

YBa

(YBCO) in bulk ceramic [67] and epitaxial ﬁlm [68] forms. In this

latter case, the extrapolated straight-line asymptote appears to reach the origin at

T D 0.

8.4 Superconductivity in Oxides 427

Fig. 8.25 Comparison of theory with measured  vs. T for the La

2x

CuO

system case. Data

are from Tarascon et al. [65]. Figure reprinted from G.F. Dionne, IEEE Trans. Magn. 27, 1190

(1991) with permission.

 1991 by the IEEE

Fig. 8.26 Comparison of theory with measured  vs. T for bulk polycrystalline and oriented ﬁlm

YBa

. Respective data are from Cava et al. [67] and Westerheim et al. [68]. Figure reprinted

from G.F. Dionne, IEEE Trans. Magn. 27, 1190 (1991) with permission.

 1991 by the IEEE

428 8 Spin Transport Properties

If x

is now subtracted from x, the concentration fraction that is available for

tunneling is the result. From this group, however, the limitations of transfer efﬁ-

ciency or probability and polaron dispersal must be taken into account. To this end,

the supercarrier density is expressed as

D P .x  x

/ D P x



1  exp





hop



; (8.38)

where x

is substituted by its deﬁnition from (8.37). A more general form of the

transfer probability P D .1  2ˇx/ represents the probability that a receptor site

is adjacent to a carrier site. For these purposes, a dispersal parameter 0  ˇ  1 is

deﬁned whereby ˇ D 0 for perfect ordering and 0.5 for random ordering; the higher

values represent various degrees of clustering. Because the transfer involves adja-

cent pairs of mixed-valence ions, the maximum value of x is 0.5 for single transfers.

Arguments can be made to support a double transfer as the minimum event (real-

space pair transfer). These concepts were discussed previously [8,23] and would be

consistent with the suggested presence of spin waves [69]. If the coherence of the

condensed state requires a two-carrier transfer as the minimum event, the factor P

would be applied twice as P

 .1  4ˇx/ and the limit of x would become 0.33.

From a concentration x

of dispersed large polarons depicted in Figs.8.23 and

8.24, a percolation threshold, deﬁned as x

D a=r

D e

=Kab

, would be reached

at the maximum temperature for which coherent tunneling can exist, i.e., the critical

temperature T

. Above this temperature there would not be enough tunneling carri-

ers to sustain the condensed state; below it, there would be excess carriers to provide

supercurrent necessary for the “perfect” diamagnetism and other properties associ-

ated with the superconducting state. Accordingly, from (8.38) T

can be related to

according to [8,9]

hop

; (8.39)

where W D ln .1  .x

=P x//

1

Since the polaron dimension also inﬂuences the spatial extent of local magnetic

frustration discussed in Sect. 8.4.2, it follows directly that the Neel temperature

would decrease monotonically with polaron density, and reach zero where the po-

laron cells merge or percolate. As a consequence, a minimum concentration for

superconduction at T

D 0 (and a maximum for magnetic order at T

D 0) will

be deﬁned as x

D x

=P , with  and P evaluated at x D x

.SinceP  1; x

will be greater than x

, particularly in the oxides if  is small because of a larger

polaron radius. In the data to be examined next, x

was determined to be 0:04 and

 0:075, consistent with the range of reported minimum polaron concentrations

(0:02  x

 0:09, from various publications) that also represent the point of total

breakdown in long-range antiferromagnetic order (T

D 0) as conﬁrmed by the data

in Fig. 8.20.

Equation (8.39) is a correction to (1.8.25) in [8], where the right-hand side was erroneously

inverted.

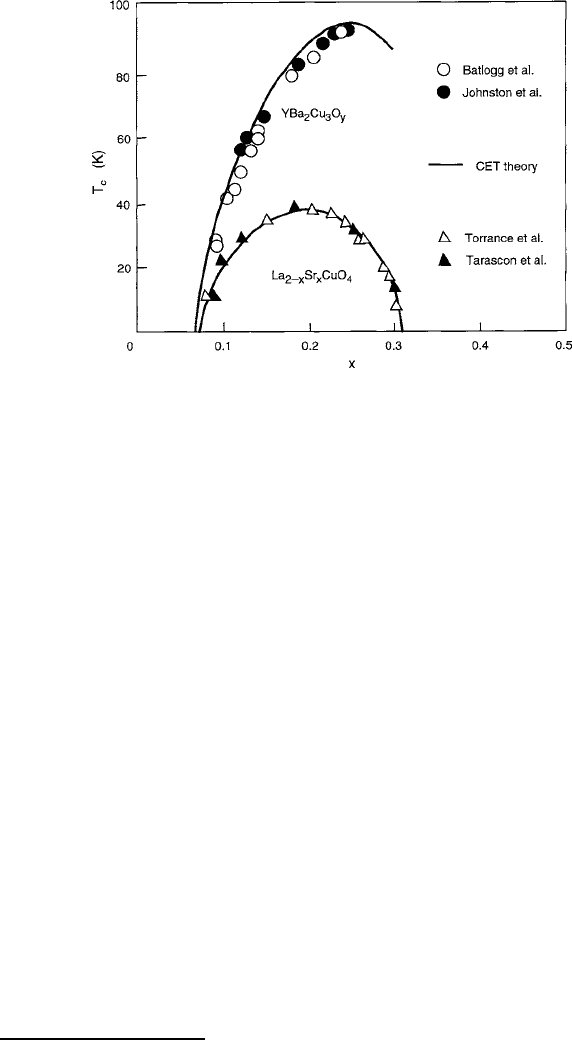
8.4 Superconductivity in Oxides 429

Fig. 8.27 Critical temperature T

vs. x for La

2x

CuO

,andYBa

(for which y has

been converted to x using the linear relation y D 0:25x 1:5). Data are from Torrance et al. [61],

Tarascon et al. [65], Johnson et al. [70], and Batlogg et al. [71]

In Fig. 8.27,theT

vs:x results of the interpretation of the experiment by means

of (8.39) are presented for hole-carrier (p-type)



2x



1x

and

YBa

compounds [61, 65, 70, 71]. To standardize the T

results in terms of

polaron ion concentration in YBa

(YBCO), x has been extracted from

the charge–balance relation y D 0:25x  1:5 for each value of y. The parabolic

character of the curves arises from the introduction of the dispersal factor P to the

W parameter. There are two readily discernible differences between the results for

the two compounds: (1) the peak in T

is greater for YBCO, suggesting that the value

of ˇ is reduced (from 0.7 to 0.57) because of better spatial ordering of the polaron

sources

and (2) the entire curve is higher, suggesting that E

hop

is increased (from

2.5 to 4meV). The implications of this latter possibility are complicated because an

increase in the polaron trap energy would result from a decrease in b

[72], which

in turn would mean that U

could have been increased by the D

ﬁeld as suggested

by the pyramidal-to-planar descent depicted in Fig. 8.18. If the transfer integral is

affected, it would also mean that the transfer probability  and the polaron radius

that determines x

would also change. As an example of the effects of the polaron

dispersal variation, Fig. 8.28 is offered for the YBCO values of E

hop

D 4 meV;x

0:035,andx

D 0:075, where it is shown that ideal ordering could theoretically

produce T

values approaching room temperature.

In these layered structures, the mixed valence in the Cu cation lattice caused by the charges of the

substitutional ions or oxygen vacancies occurs in the crystallographic layer of the Cu–O

planes.

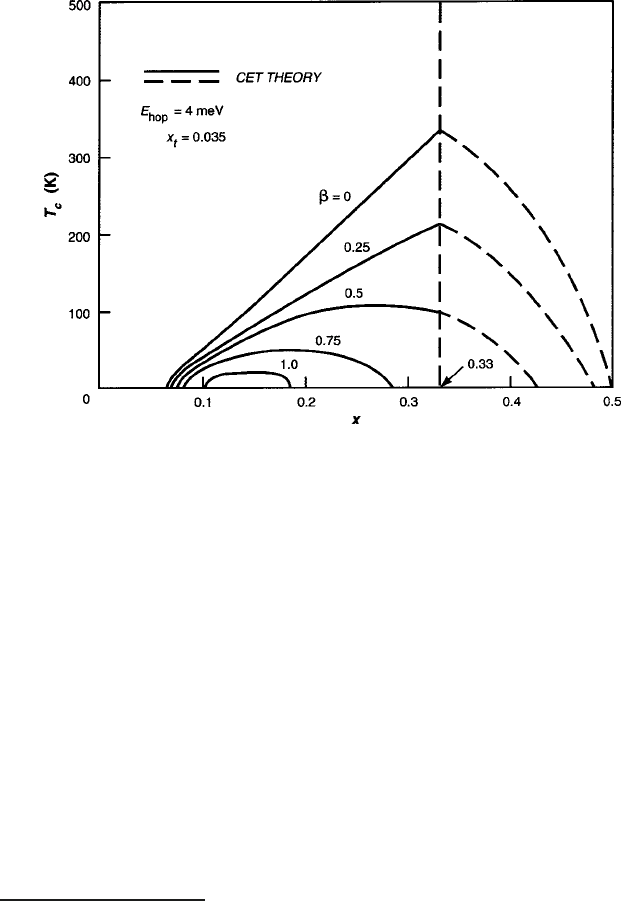
430 8 Spin Transport Properties

Fig. 8.28 Projected T

vs. x curves over the range of 0  ˇ  2 for individual carriers and

0  ˇ  1 for pairs. Dashed curves indicate that the “real-space” pair model does not apply

beyond x D 0:33

8.4.5 Layered Cuprate Superconductors

It is appropriate to begin this discussion with a review of the orbital states and

occupancies of the Cu

–O

2

–Cu

superexchange combination, which leads to

p-type superconduction that is conﬁned to select Cu–O

planes that occur as part of

the B-lattice oxygen coordinations in perovskite-type lattices. Although the large-

polaron concept implies that the region of mixed-valence condition is local, with

carriers tethered to ﬁxed polaron sources, it should be emphasized that the valence

state is not a ﬁxed entity in cases where itinerant polarons exist through extended

covalent delocalization. In accord with the .CuO/

molecular ion concept,

the

transfer cations in these partially covalent compounds assume average (noninteger)

valences lower than their nominal ionic assignments because the carrier electrons

The

CuO

molecule in this model is Cu

2

, where the “hole” carriers tunnel as part of

the antibonding chain formed from the d

y

 2p. A second possibility that has received

attention is the peroxide option in which the balancing of the electronic charge is not the result

of a third ionization of the Cu atom, but rather by the reduction of the negative charge on the O

to create a Cu

1

molecule. In this case, the Cu

ion acts as an acceptor in a band model

semiconductor sense, leaving the hole carriers in the O

2

band. An immediate distinction from

the former approach is that the transportable spin could traverse the anion lattice through direct 

linkages. The interested reader is encouraged to consult the publications of K. Johnson that describe

a novel approach to superconductivity and its relation to dynamic Jahn–Teller effects [74,75].

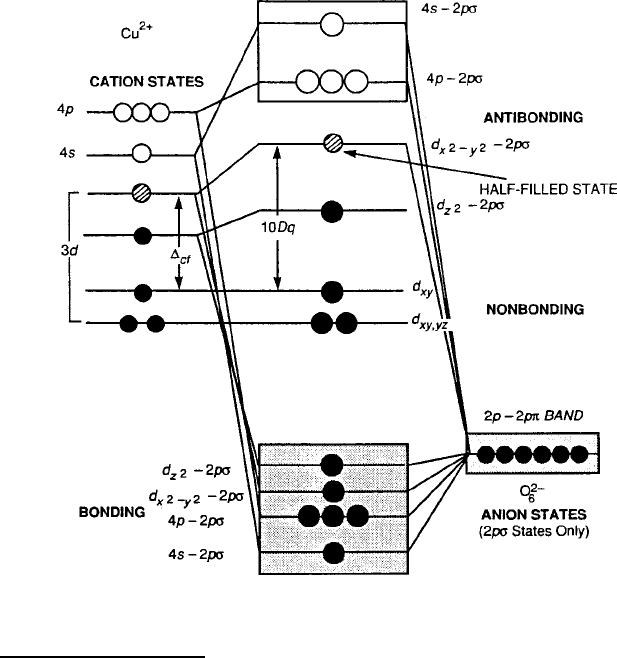
8.4 Superconductivity in Oxides 431

become shared among the ions, both Cu and O, within the large-polaron cell.

These effects of covalent bonding may be estimated from the orbital reduction

factors of transition-metal complexes as determined for paramagnetic resonance

measurements of g-factors and spin–orbit coupling constants. In the case of Cu

in Tutton salts, for example, the reduction is about 15% [73]; if applied to the ox-

ide, this would mean that the actual ionic charges would be Cu

1:7C

1:7

. For want

of a suitable systematic means for determining these effective valences, however,

the integer valence values of the free ion oxidation states will be maintained in the

discussions that follow.

To examine covalence involving the unﬁlled d shell of a transition series, it is ﬁrst

necessary to establish the crystal-ﬁeld (point-charge model of ionic lattice) split-

tings for the particular system. The order of energy levels for the ﬁve 3d orbital

states shown for the Mn–O

octahedral coordination .O

/ in Fig. 2.34 is adjusted to

the tetragonal .D

/ case in Fig. 8.29 for the Cu

cation. For a c-axis extension,

Fig. 8.29 MO diagram for a tetragonally

distorted CuO

complex [9]

This traditional view has also been expressed by A.W. Sleight in a review of superconducting

oxide chemistry [76].