Dionne G.F. Magnetic Oxides
Подождите немного. Документ загружается.

392 8 Spin Transport Properties
Incoherent electrical conduction by thermal hopping is significant where E
hop
is
small or temperature is large. Because spin alignment determines U
ex
in a magnetic
material, the term magnetic polaron can be added to the lexicon. In simple terms,
when neighboring spins of the trapped carrier are aligned parallel, the local envi-
ronment of the carrier is ferromagnetic and cos D 1, thereby removing the U
ex
part of the polaron trap. The carrier would then be constrained only by its dielectric
(elastic) trap. The ferromagnetic polaron therefore has the transport properties of a
conventional dielectric polaron.
8.1.3 Transfer by Covalent Tunneling
At low temperatures, a more efficient transfer mechanism can produce remarkable
effects when the right conditions of chemical bonding and spin ordering are present.
In the context of molecular-orbital states charge transfer can also be viewed as a
quantum mechanical probability stemming directly from the covalent bond, i.e.,
through a “covalent-transfer” mechanism. This concept can be readily appreciated
by imagining the concentric ring diagram in Fig.8.2 as analogous to a hydrogen
atom (with reversed polarity in this case), where the rings would represent a se-
ries of higher energy states. The wavefunction of the mobile polaron charge could
then be viewed as an s orbital wavefunction and its probability of occupancy at
a distance r from the source would then be determined by its contribution to the
molecular-orbital state as the carrier moves toward the outer rings. Such an exercise
can be approximated from the eigenfunctions of (8.6) after being modified to antic-
ipate the variable polaron trap energy U
p
.r/ of (8.10) and is sketched in the energy
level diagram of Fig. 8.3.
For the small polaron limit b
2
p
.E
a
E
b
/
2
D U
2
p
, application of the proce-
dureusedtoderive(8.6) yields
'
small
C
1
p
2
1
b
p
2U
p
2
!
1
2
'
a
C
b
p
2U
p
'
b
(8.11)
and the transfer probability of the polaron carrier from site a to site b can be defined
as the square of the coefficient c
ab
of '
b
. If we define a transfer efficiency as the
ratio of the two probabilities
.r/
small
b
p
=2U
p
2
1
b
p
=2U
p
2
b
p
2U
p
2
; (8.12)
which tends toward zero in this approximation, thereby confirming the ineffective-
ness of quantum tunneling to extend the range of the carrier beyond the small-
polaron ring.
8.1 Polarons and Charge Transfer 393
For the large polaron limit b
2
p
U
2
p
,the'
C
eigenfunction for a bonding state
with the coefficients defined in (8.6), would be
'
large
C
1
p
2
"
1 C
U
p
b
p
1
2
'
a
C
1
U
p
b
p
1
2
'
b
#
; (8.13)
and
.r/
large
c
2
ab
c
2
aa
1 U
p
=b
p
1 C U
p
=b
p
1
2U
p
b
p
: (8.14)
From the electrostatic attraction between two oppositely charged particles in a
medium of dielectric constant K and M
a
to M
b
dimension a,ther-dependent part
of U
p
becomes
U
0
.r/
e
2
K
1
a
1
r
e
2
Ka
1
a
r
: (8.15)
Therefore, the charge-transfer probabilities can be related to quantum mechanical
tunneling to a distance r from the polaron source by substituting (8.15) (or another
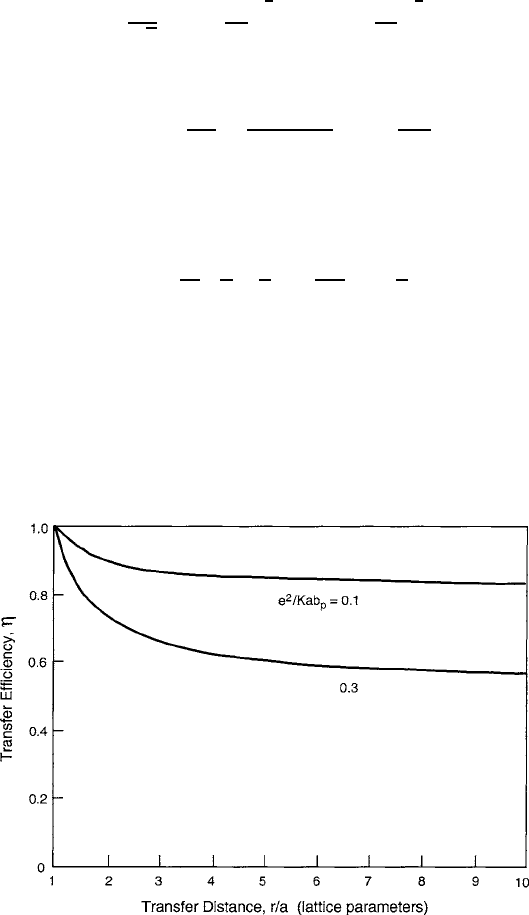
appropriate function) into (8.12)and(8.14). Figure 8.4 compares the efficiency pa-
rameter variation with r=a for large polarons. A somewhat more rigorous approach
would consider consecutive discrete transfers of the polaron carrier from its source.
To this point, the only reference to temperature has been in relation to the Boltzmann
Fig. 8.4 Polaron transfer efficiency as a function of reduced lattice length for two ratios of elec-
trostatic energy to polaron half-bandwidth

394 8 Spin Transport Properties
activation probability. Although not stated explicitly, there is a T dependence of the
spin alignment that is characterized by the Curie temperature through the Brillouin–
Weiss theory. The temperature will also affect the value of E
hop
and the extent to
which tunneling is allowed to control the lifetime of the polaron in its trap. However,
even if perfect spin alignment were possible, lattice vibrations would still create a
temperature dependence of b
p
, which will now be related to a polaron bandwidth.
8.1.4 The Holstein Polaron Theory
In his quantum mechanical analysis of polaron motion [6]. Holstein defined three
stages of conductivity that were determined by the relative magnitudes of two en-
ergy parameters (1) the polaronic charge exchange energy b
p
, which establishes the
lifetime
p
of the polaron carrier in its site according to
p
„=b
p
, and thereby
presents b
p
as the width of the polaron energy band that is the product of the full
electronic exchange integral b and a lattice vibronic coupling factor, and (2) the en-
ergy U
p
of the electrostatic potential well in which the carrier resides and which is
shaped by the charge of the carrier and a neighboring charge of opposite sign that
created it, i.e., the other half of an extendible dipole. The temperature dependence of
b
p
is determined by the number of vibrational modes (phonons) available to interact
with the carriers. The vibrational overlap integral is a decreasing function of T and
its contribution to b
p
is maximum at absolute zero, diminishing rapidly with rising
temperatures.
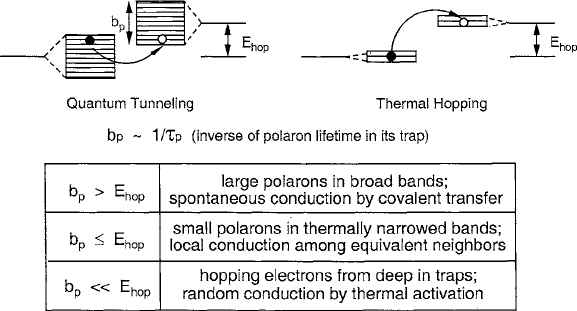
Based on these concepts, Holstein defined the criterion for a large polaron (one in
which the carrier extends beyond its immediate environment by spontaneous charge
transfer) if b
p
E
hop
, and that of a small polaron (which is limited to its imme-
diate neighboring sites) if b
p
<E
hop
. These transfer mechanisms are often referred
to as coherent or adiabatic because of their energy conserving nature. In the final
stage which sets in at higher temperatures, the metallic conductivity begins to break
down and semiconduction by incoherent nonadiabatic electron hopping becomes
dominant. With increasing temperatures, the large polaron condition begins to fail
because higher-frequency lattice vibrations allow the carriers to stabilize in their
traps by permitting elastic adjustments to occur more quickly, thereby lengthening
the polaron lifetime of
p
. This action leads to a decrease in b
p
which begins to set
in as the temperature approaches the Debye temperature
D
.
2
2
The relation between the Debye energy k
D
and U
p
in determining the actual activation energy
E
hop
can be appreciated if one recognizes that the electrostatic potential of the polaron dipole field
has an intimate tie to the elastic distortion that dresses the polaron charge site. The distortion of the
lattice can be viewed as a reaction to the dipolar field and both energies involve the polarizability of
the lattice through the dielectric constant K. As origins of the trap energy, they could be considered
to have some equivalence.
8.1 Polarons and Charge Transfer 395
The polaron bandwidth b
p
is reduced by vibronic (orbit–lattice) coupling that
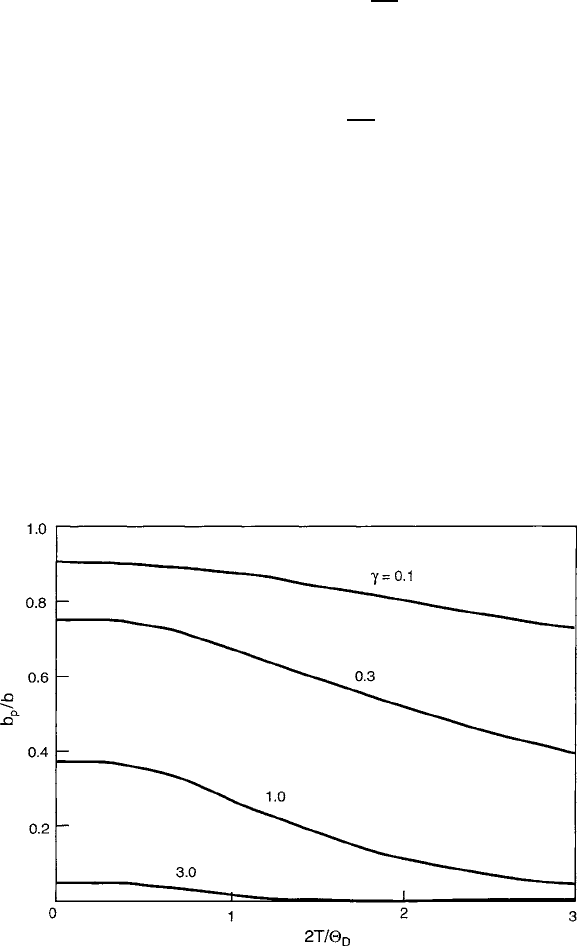
produces a temperature-dependent narrowing given by [12].
b
p
.T / D b exp
coth
D
2T
(8.16)
that ranges from b
p
.T / D b exp .–/ at T D 0 to the simplification
b
p
.T / D b exp
T
D
; (8.17)
when T
D
=2.
Although not readily discernible in this brief summary, another facet of
Holstein’s model is that the threshold where thermal activation becomes a significant
competitor to tunneling is T
D
=2. As seen in the complete function (8.16) plot-
ted in Fig. 8.5, the polaron bandwidth is still a sizable fraction of b exp ./ at this
point. The parameter 50=K
2
opt
would be 0.2 to 2.0 for transition-metal oxides
with an optical dielectric constant K
opt
in the 15 to 5 range. As a consequence,
the decrease in b
p
will eventually serve to reduce the carrier population according
to a probability approximated by the Boltzmann relation exp
E
hop
=kT
in the
usual diffusion relation for electron hopping by thermal activation. Therefore, the
transport of a polaronic carrier requires that an increase in energy E
hop
be supplied
to remove it from its trap. A qualitative summary of the polaron stages is presented
in Fig. 8.6.
Fig. 8.5 Reduced polaron bandwidth as a function of reduced temperature for different values of
396 8 Spin Transport Properties
Fig. 8.6 Diagram of polaron stages based on the relative magnitudes of b
p
and E
hop
8.2 Metallic Oxides with Polarized Spins
For electronic conduction in solids, two conditions must be satisfied (1) there must
be charge carriers and (2) there must be a mechanism to enable their transport.
Carriers can be “free,” as in collective-electron metals, excited as in band-model
semiconductors, or activated from polaron traps in ionic compounds. The second
requirement involves the environment of the destination sites and what lies in be-
tween, i.e., the mobility. The temperature dependence of these variables is what
generally defines whether the material is a metal (carrier density decreasing with T )
or insulator (both carrier density and mobility increasing with T ). There is, how-
ever, another significant distinction that applies particularly to magnetically ordered
materials.
Charge carriers in metals are drawn mainly from s and p states, despite the for-
mation of hybrids with d states in the collective intermingling. As a result, the
d -electron magnetic carriers represent only a fraction of the population that pro-
duces current. In transition-metal oxides, the s and p electrons of the cations are
transferred to the oxygen to establish the anion lattice, and have only negligible hy-
brid mixing with the d shell. Therefore, in the rare situations where the d electrons
become itinerant, the current has the spin polarization of the transfer states, which
is usually ferromagnetic in contrast to the more random situation in a ferromagnetic
metal. Since the vast majority of the carriers are of only one spin orientation, metal-
lic compounds of the transition-metal series are frequently called “half-metals.” The
possible origins of polarized spin transport in select metallic oxides can be reviewed
in the context of molecular-orbital theory.
In systems where only the t
2g
orbital states are occupied, i.e., the lighter mem-
bers of a 3d
n
transition series, metallic conduction can occur if the t
2g
levels retain
a degeneracy in a lower symmetry crystal field. The most common occurrences are
found with d
1
and d
2
configurations in simple monocation-site compounds. Be-
8.2 Metallic Oxides with Polarized Spins 397
cause the cation sites are principally octahedral, the t
2g
electrons usually form weak
bonds to the O
2
anions and therefore feature small exchange stabilization that
would normally be expected to provide low antiferromagnetic N´eel temperatures
T
N
. At room temperature, even with dynamic Jahn–Teller (J–T) or spin–orbit (S–O)
splittings
10
2
eV
of the triplet, the t
2g
states would then form partially filled
t
2g
–p–t
2g
states resulting from the localized metal–ligand–metal superexchange
[8,9].
8.2.1 Simple Oxides
In cases such as TiO and TiO
2
, single d electron transfer can occur as a result
of hopping electron between 3C and 4C mixed-valence states of the Ti ions when
the compound is off stoichiometry, e.g., from O
2
vacancies. Spontaneous magnetic
ordering is usually not involved here because the spin density is too small to produce
anything but paramagnetism. A more interesting situation occurs with stoichiomet-
ric CrO
2
3d
2
. The crystal structure is rutile (tetragonal cation site symmetry D
4h
with c=a <1), which splits the t
2g
triplet into a lower d
xy
singlet and an upper d
xz:yz
doublet, as sketched in Fig. 8.7a. The molecular-orbital hybrid states populated ac-
cording to the Aufbau qualitative guidelines would then have a single electron in
each level, but with competing spin-polarization tendencies. In the lower state, the
half-filled d
xy
–p–d
xy
hybrid would be expected to follow the rules of antifer-
romagnetic superexchange [13]. In the upper d
xz:yz
–p–d
xz:yz
doublet, however,
Hund’s rule high-spin alignment can exist within the two orthogonal states because
the degeneracy allows the two electrons to select different orbitals, thereby avoiding
the Pauli principle while providing ferromagnetic exchange stabilization through
itinerant charge-transfer characteristic of metallic conduction [8, 9]. The net result
would be determined by the spin configuration that produces the lowest energy.
Consequently, the antibonding half of d
xy
–p–d
xy
is stabilized to accommodate
the electrons with the lower energy SD1 parallel spin alignment. The ferromag-
netic order gives the full 2m
B
magnetic moment per cation (100% polarization) at
low temperatures and coexists with metallic conductivity up to a Curie temperature
of 400 K [14,15]. A more in-depth discussion of the various orbital interactions that
lead to the magnetic order and electrical conductivity of these compounds is given
by Goodenough [16].
8.2.2 Complex Oxides
Another uncommon situation occurs in mixed (or double) perovskites (Fig. 8.1)
in which charge-ordered dissimilar octahedral-site cations can produce metal-
lic conduction and long-range spin order that reach above room temperature.
AprimeexampleisSr
2
2C
Fe
3C
Mo
5C
O
6
[17]. The charge-transfer and mag-
netic properties are believed to originate from the half-filled/half-filled correlation
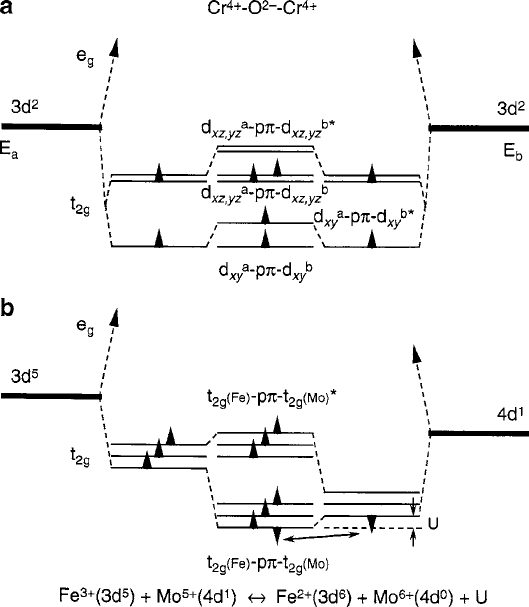
398 8 Spin Transport Properties
Fig. 8.7 Molecular-orbital approximations for two special cases of spin-polarized metallic charge
transfer: (a)Cr
4C
O
2
3d
2
where a ferromagnetic moment occurs because of the survival of a
spin–orbit d
xz;yz
doublet that forms a “band” with partially filled orthogonal states allowing Hund’s
rule to apply and (b)Sr
2
2C
Fe
3C
Mo
5C
O
6
, which is a paramagnet/unbalanced antiferromag-
net (quasi-ferrite) that occurs by delocalization superexchange involving the sharing of the single
Mo
5C
electron. Oxygen ligand states are not shown
superexchange [13] between the two lowest states of Fe
3C
3t
2g
3
e
g
2
and
Mo
5C
5t
2g
1
e
g
0
that form the 3d
xy
.Fe/ –2p–5d
xy
(Mo) hybrid in the B sub-
lattice. Antiferromagnetism is expected in this case, but with a net “ferrimagnetic”
moment associated with the remaining four unpaired spins of the Fe
3C
ion. As a
consequence, the compound is a quasi-ferrimagnet with only one crystallographic
sublattice and only one molecular-field coefficient. If this material were an ideal un-
canted ferrimagnet, the magnetic moment per formula unit would be 4m
B
. Although
measurements indicate that the actual value at low temperatures is closer to 3m
B
,
the conductivity is still metallic. One possible explanation can be gleaned from
the molecular-orbital model in Fig. 8.7b. Beginning with the conductivity issue, we
can reason that the single spin resident in the t
2g
shell of the Mo
5C
5d
1
ion is
shared with the Fe
3C
3d
5
ion by delocalization exchange. Since the outermost
8.2 Metallic Oxides with Polarized Spins 399
electron of the Fe
2C
3d
6
ion is loosely bound in a filled d
xy
orbital, i.e., the first
one added to the half-filled t
2g
shell, we can argue that two ionic configurations can
exist simultaneously through spin transfer reactions
Fe
3C
C Mo
5C
, Fe
2C
C Mo
6C
C U
eff
t
2g
3
e
g
2
C t
2g
1
e
g
0
, t
2g
4
e
g
2
C t
2g
0
e
g
0
C U
eff
The degree of sharing and hence the mobility of the single Mo
5C
spin will de-
pend on the relative magnitudes of U
eff
and b,whereU
eff
is the difference in the
binding energy between the initial and final states of the transfer and b is the ex-
change integral between the Fe and Mo ions mediated by the O
2
ligand (not
shown in Fig. 7b). If the single Mo
5C
spin becomes itinerant in this sense, spin-
polarized transport could take place in the narrow half-filled band constructed from
the 3d
xy
.Fe/ –2p–5d
xy
(Mo) hybrid. Inspection of the above charge-transferreac-
tions reveals that the left-hand side represents an antiferromagnet (or a quasi-ferrite)
and the right-hand side a paramagnet. Therefore, the probability of obtaining the
maximum 4m
B
is reduced by the probability of paramagnetism that occurs when
Mo
5C
is missing its t
2g
spin. If a paramagnetic contribution is present, experiments
at very high magnetic fields might help to clarify the situation.
Another point of interest is that the 3m
B
value of the net magnetic moment per
molecule lends credence to the suggestion that the Goodenough–Kanamori (G–K)
rules [9] for predicting the most probable type of spin ordering might not apply in
this case. If only the e
g
states are considered because of the conventional wisdom
that the t
2g
–p hybrids are effectively nonbonding and can be ignored, the logical
conclusion for 180
ı
¢ bonding of the perovskites is that ferromagnetic delocaliza-
tion exchange will result between the empty Mo
5C
and half-filled Fe
3C
e
g
shells,
producing magnetic moment limit of 6m
B
. However, the experimental result of 3m
B
suggests that the d
xy
–p bond of the t
2g
shell is strong enough to stabilize the type
of ferrimagnetic ordering proposed.
In a series of compositions with Cr, Mn, and Co used in place of Fe, [18] ferro-
magnetism was found only with Cr. Since it assumes its 3C valence with a highly
stable electronic configuration t
2g
3
e
g
0
, 3d
3
-d
1
antiferromagnetic (ferrimagnetic)
superexchange is again the likely result. No evidence of metallic conduction was
reported, however, which suggests that the value of U
eff
is greater than that of the
Fe case. The other ions also showed insulating properties, but no magnetic order-
ing. The prospects of antiferromagnetism are reduced because the most stable forms
of Mn and Co are divalent, which would force the Mo valence to be raised to the
diamagnetic 6C state, thereby lowering the chance of spontaneous magnetism. Sim-
ilar analysis can be applied to other combinations of transition metals, such as Ti,
W, and Re, but the prospects for strong superexchange with spin-polarized metallic
conductivity between the alternating B-site cations probably remains highest with a
d
5
–d
1
combination.
Ferromagnetism in metallic oxides also occurs with spins in the e
g
shell of
the mixed-valence perovskite
La
3C
1x
Ca
x
2C
Mn
3C
1x
Mn
x
4C
O
3
, for temperatures
reaching above 300 K. The origins of this ferromagnetism are complex and are

400 8 Spin Transport Properties
discussed in Sect. 8.3.1. Normally when the e
g
shell is occupied, strong ¢ bonds are
formed that produce antiferromagnetic stabilizations that can survive to well above
room temperature. Simple oxides of the heavier 3d
n
elements, MnO through CuO,
all feature antiferromagnetism and usually p-type semiconduction when mixed va-
lence occurs, despite the ferromagnetic tendencies that can still exist with the t
2g
shell partially filled.
8.2.3 Classical Resistivity–Temperature Model
Returning to the discussion that produced (8.10), we can now examine the ques-
tion of conductivity in polaronic oxides. Most transition-metal oxides are termed
mobility-activatedsemiconductors in contrast to more conventionalband model ver-
sion with the usual description of holes and electrons dictated by Fermi statistics.
The electrical resistivity of mixed-valence oxides obeys the standard relation for
mobility-activated semiconduction in which the polaron trap energy E
hop
and the
activation energy are equivalent in the temperature regime where random hopping
is dominant [19–22],
D
x
eff
V
e
eD
kT
1
exp
eD
kT
; (8.18)
where the carrier concentration per chemical formula unit, x
eff
D n
eff
=V , the ratio
of the volume carrier density to the volume of a formula unit V , the factor (eD/kT )
is the Einstein diffusion mobility, and D the diffusion constant that equals the ratio
of the square of the mean-free path to the carrier lifetime d
2
hop
=
hop
. To account for
the probability of a transfer being completed, an effective carrier concentration is
defined by x
eff
D xP ,whereP is a polaron dispersal probability equal to (1 x)for
a random distribution. Further dependencies of relevance are that
hop
D
1
hop
,which
is on the order of the Debye frequency and d a=.1x/ to account for the average
hop distance as a function of concentration [23]. Upon substituting appropriately
into (8.18), a working expression for the resistivity becomes
D
C.1 x/ kT
x
exp
E
hop
kT
D
C.1 x/ kT
x
for kT E
hop
; (8.19)
where C D V=e
2
a
2
hop
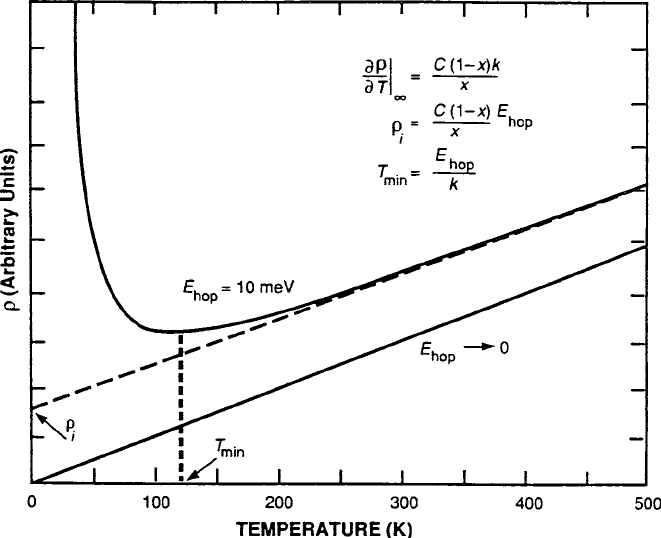
. As illustrated in Fig. 8.8, plotted as a function of T
for E
hop
D 10 meV from (8.19) will show insulating behavior (decreasing) at low
temperatures and pass through a minimum at T D E
hop
=k.AsT increases further,
the curve will approach a metallic straight line of (increasing) slope C .1–x/ k=x.
Note that the asymptote of the curve will pass through the origin at T D 0,which
is a result that is not expected in experiment because residual resistivity
i
effects
would appear. This model is discussed further in relation to superconductivity in
Sect. 8.4.
8.3 Magnetoresistance in Oxides (CMR) 401
Fig. 8.8 Generic plots of vs. T for E
hop
D 0 and 10 meV, defining relations for T
min
,and
asymptote slope @=@T j
1
and intercept
i
. Figure reprinted from G.F. Dionne, IEEE Trans. Magn.
27, 1190 (1991) with permission.
c
1991 by the IEEE
The temperature of metal–insulator transition therefore resides in the value of
E
hop
, which from (8.10) is controlled greatly by the magnetic state of the spin
system. There are two prominent examples where E
hop
is reduced to the basic elas-
tic polaron limit E
0
hop
D U
0
p
by the absence or removal of E
ex
hop
.D U
ex
/.Ifthe
spins are collinear, cos D 1 and E
ex
hop
0. In oxides, this condition is uncom-
mon because superexchange usually dominates to produce antiferromagnetism. An
important exception can occur with Mn ions in certain ferromagnetic perovskites
compounds that feature metallic properties but also display large magnetoresistance
effects at the Curie temperature.
8.3 Magnetoresistance in Oxides (CMR)
In the generic
RE
3C
A
2C
MnO
3
perovskite system, the conditions for metal-
lic conduction in the Mn sublattice can occur in a ferromagnetic phase that ap-
pears at lower temperatures. When the ferromagnetism is dissipated at the Curie
