Dionne G.F. Magnetic Oxides

Подождите немного. Документ загружается.

362 7 Magneto-Optical Properties

strengths for the separated transitions that interact, respectively, with right- and

left-handed circularly polarized waves [16, 19]. A diamagnetic transition results

from a L  S splitting of the excited state, characteristic of BiYIG compounds

[25, 26]. The frequency dependence of "

and "

in the diamagnetic case presents

line shapes nearly the reverse of those of the paramagnetic case [16], which is con-

venient for identiﬁcation purposes. Note also that because spin–orbit interaction

organizes the orbital angular momentum L

D˙1 states in either case, the asso-

ciated spin S

states must be aligned in a saturating magnetic ﬁeld to produce an

observable cooperative effect.

Figure7.10 presents the results of the diagonal tensor elements, and Fig. 7.11

shows the Kerr ellipticity and rotation. The identiﬁcation of the transitions re-

sponsible for the spectra of the diagonal elements was accomplished by ﬁtting the

imaginary part to the Gaussian peaks shown in Fig. 7.12, with the parameter values

listed in Table7.2. The exercise was begun by assuming energy values correspond-

ing to the features of the measured spectrum. Moreover, to match the data for "

at energies above 4 eV found in the literature [21,22], a strong charge-transfer tran-

sition was assumed at 4.35eV. The Gaussian curve ﬁt to the "

spectrum compares

well with ﬁts achieved by others [27, 28]. Most notable is the agreement with the

onset of strong absorption peaks commencing at approximately 2.85 eV.

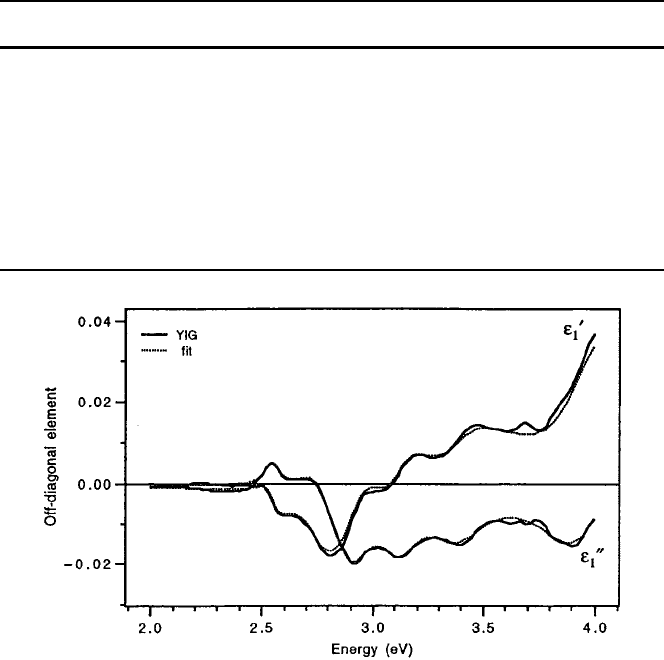
The "

spectra were ﬁt by assuming a series of paramagnetic transitions [23,

24]. The agreement shown in Fig. 7.13 was accomplished with the parameters listed

in Table 7.2. Note the correspondence with the transition energies found from the ﬁt

to the spectrum of "

. An exception is a transition at 3.93 eV which has no match

in the Gaussian curve ﬁt to "

. To extend the agreement with data in the literature

[21,22] for energies above 4 eV, we added the strong paramagnetic transition in the

vicinity of 4.35 eV.

The widths of the magneto-optical peaks listed in Table 7.2 are generally smaller

than those of the "

spectra. The "

spectrum was modeled with Gaussian functions

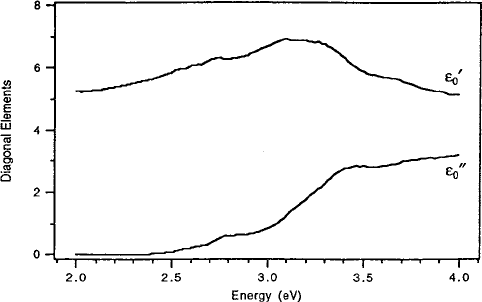
Fig. 7.10 Measured spectra of the real and imaginary parts of "

for YIG. Figure reprinted from

[24] with permission.

 2003 by the American Institute of Physics

7.3 Magneto-Optical Spectra 363

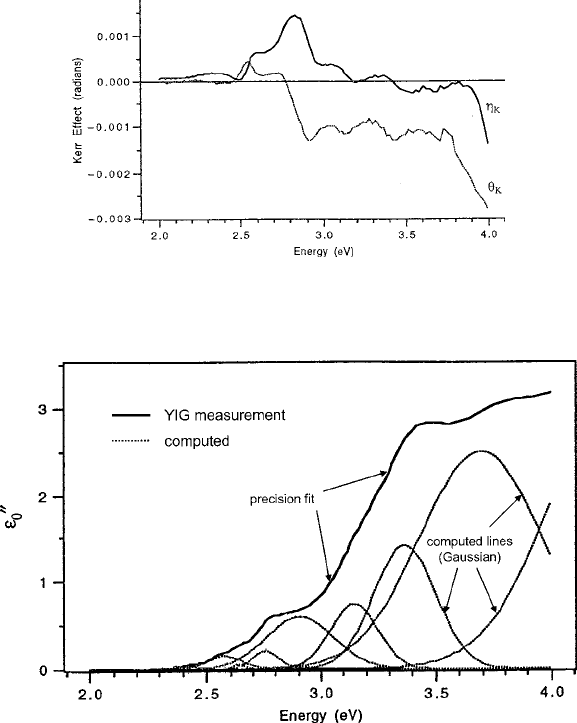
Fig. 7.11 Measured Kerr ellipticity and rotation of YIG. Figure reprinted from [24] with

permission.

 2003 by the American Institute of Physics

Fig. 7.12 Precision ﬁt of Gaussian curves to data of "

. Computed and measured curves are almost

perfectly coincident. Individual computed curves are shown. The parameters used in the ﬁtting are

listed in Table. 7.2 Images are reproduced from Allen’s doctoral thesis [23]. Figure reprinted from

[24] with permission.

 2003 by the American Institute of Physics

of half-width 

determined at the e

1

point relative to the peak value, while the

Lorentzian shapes assumed for the "

components have smaller half-widths 

when

characterized by values at half maximum.

From the numerical results obtained from curve ﬁts of "

and "

,(7.38) was used

to determine the quantity N=N listed in Table7.2 for each transition. Note that the

spectrum consists entirely of paramagnetic transitions. This result is surprising

because the ground state of the Fe

ions is a

S term, with no orbital angular

momentum. An explanation for the acquisition of orbital angular momentum by the

364 7 Magneto-Optical Properties

Table 7.2 Permittivity and ground-state splittings of Y



2





eV 10

2





2





eV 10

2



jN=N j

j



eV 10

3



2.41 3.0 8:02 –– ––

2.58 14.2 10:6 1:16 4.2 0.082 4.1

2.64 4.4 3:9 –– ––

2.73 19.4 8:3 1:23 8.4 0.063 3.15

2.90 58.8 20:7 3:58 11.0 0.061 3.05

3.15 73.5 14:6 2.40 10.8 0.033 1.65

3.37 141 18:8 2.28 16.5 0.016 0.80

3.70 250 37:1 –– ––

3.93 – – 5.36 23.8 – –

4.35 338 43:1 8:25 35.0 0.024 1.20

Fig. 7.13 Lorentzian curve ﬁts to "

and "

. The parameters used in the ﬁtting are listed in

Table. 7.2 Figure reprinted from [24] with permission.

 2003 by the American Institute of

Physics

iron ion ground state from excited terms within the ion was proposed by Clogston

[29] and later reﬁned by Scott et al. [20]. For the present exercise, a partial solution

of an intersublattice covalent model is attempted.

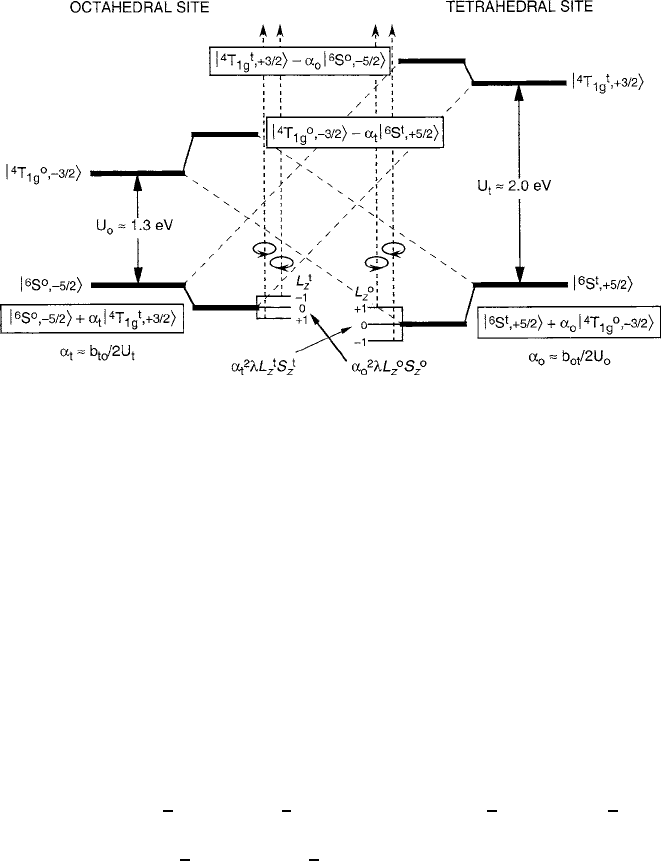
Listed in Table7.2 are the 

magnitudes of the L

-degenerate ground-state

component split by spin–orbit coupling. In a ferrimagnetic spin system, superex-

change stabilizes the maximum stationary value of spin component S

of the Fe

ions in both octahedral and tetrahedral sites. The attendant covalent interaction

also produces molecular-orbital states that hybridize the orbitals of the octahe-

dral

and tetrahedral

terms in a bonding state that correlates the electrons

into an antiferromagnetic spin alignment. More relevant to the present discus-

sion, however, is the hybridization of the octahedral

D –5=2/ term with

the lowest excited term

DC3=2/ of the neighboring tetrahedral site, and

7.3 Magneto-Optical Spectra 365

Fig. 7.14 Molecular-orbital model of the

mixing into the

S ground state of the opposing

magnetic sublattice. Similar models can be made for the intrasublattice covalent mixing. Figure

reprinted from [24] with permission.

 2003 by the American Institute of Physics

vice versa with respect to

and

.TheS

values are adopted from the

exchange energy perturbation used by Clogston [29]. Illustrated schematically in

Fig. 7.14 are ground states reﬂecting a small orbitally degenerate component from

the opposing sublattice

(and higher) terms. The unnormalized hybrid ground

terms

; 5=2iC˛

; C3=2i and

; C5=2iC˛

; 3=2i,where

and ˛

are the respective mixing fractions which are given by the relevant factor

=2U

, half of the ratio of the transfer integral to the energy difference between the

relevant states of the two cations.

If the T

triplet is treated as a quasi-P state, the ground-state splitting from

L  S D ŒL

C .1=2/ .L



C L



/ arises from the L

D˙1 differ-

ence of the i-site diagonal matrix elements, which simpliﬁes to



D 2



; 

C ˛



; C





C L



; 



C˛

; C



 2˛



; C

L

; C



 3˛

: (7.39)

For the 3d

, 0:06 eV and b

0:5 eV (in oxides). The U

i;j

values [24] indicated

in Fig. 7.14 result in ˛

10

2

, which is sufﬁcient to account for the 

splittings

that approach 5 meV as deduced from N=N values.

Although the concept of cross transfers between sublattices is speculative, there

is further evidence that these effects can provide indirect avenues to satisfy the

S D 0 selection rule. This subject will be revisited after the anomalous diamag-

netic contributions of Bi

in YIG are reviewed.

366 7 Magneto-Optical Properties

7.3.3 Iron Garnets with Bismuth Ions (Diamagnetic)

In stark contrast to the theoretical spectra constructed from split ground state

paramagnetic transitions that served to provide a high precision ﬁt to the magneto-

optical properties of Y

, the story of the remarkable enhancement of Faraday

rotation when Bi

ions are substituted for Y

, reported originally by Buhrer in

1969 will be outlined [30]. Rather than a population-sensitive split ground state, it

is the splitting of the excited

P state by spin–orbit coupling that produces the large

value of the off-diagonal tensor element "

, but only for select transitions in the

ions in the magnetically opposed octahedral and tetrahedral sublattices [26].

Similar to the curve-ﬁtting exercise described above, the approach adopted is based

directly on the interpretation of reported data. The analysis is based on the over-

lapping of three diamagnetic-type Fe

transitions that are inﬂuenced by covalent

interactions with Bi

ions.

For ferrimagnetic systems, the orbital singlet ground state

S of Fe

ions is

unperturbed by the strong superexchange ﬁeld that inﬂuences only the spin system

(Sect. 7.1). For this reason, interpretation of the rotation and ellipticity spectra from

3x

must logically be based on the diamagnetic functions described by

the off-diagonal permittivity tensor elements "

D "

C i"

, according to [25]

D !





0˙

 !

 



C i



0˙

C !

C 





0˙

 !

C 



C 4!



; (7.40)

where !

D 4Ne

=m;!

0˙

D !

˙,andN is the density of transition centers.

The oscillator strengths for the positive and negative rotations are f

˙f=2

[which denotes a subtraction occurring in (7.40)]. If we introduce the excited state

splitting, f

 .˙f=2/.1˙ =!

/, as determined by Allen and Dionne [17].

If this expression is separated into real and imaginary parts without approxima-

tions, one obtains separate relations for the "

and "

, which may be used to compute

Faraday and Kerr rotations and ellipticities [22]. For the magnetic garnets at energies

below 2.5 eV, the diagonal elements of the tensor "

 n

(n is the index of refrac-

tion  2:3 in this regime) and "

 0. The Faraday rotation constant is given by



 .!=cn/ "

; (7.41)

For this system, both "

and "

are only modestly increased by Bi

substitutions.

These features make (7.41) accurate for use in this energy regime [22].

From inspection of the magnetic garnet magneto-optical data in the literature,

one can identify two general groupings (1) Kerr effect ellipsometry measurements

To remain consistent with the literature of this problem, the frequently-used parameter !

introduced. Its relation to the parameter !

deﬁned to simplify the analysis in Sect. 7.3.1. is given

by !

0˙

D !

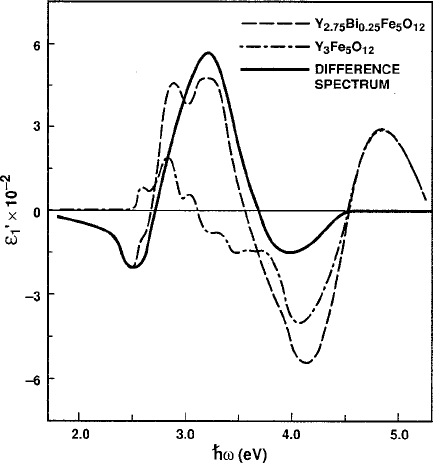
7.3 Magneto-Optical Spectra 367

Fig. 7.15 Y

3x

data of Wittekoek et al. [21], showing the difference curve formed

from the subtraction of the x D 0 and 0.25 curves. Figure reprinted from [25] with permission.



1993 by the American Institute of Physics

of "

and "

as a function of spectral energy over the range from 2 to 5 eV and

(2) 

transmission measurements in the range below 2 eV. Although Faraday

rotation effects are of practical importance at lower energies, the major optical

events take place at higher energies. It is reﬂection data from the Kerr effects, there-

fore, that provide the fundamental clues to the source of the phenomena. According

to published data [21, 31], the major peak in "

lies between 3 and 3.5eV.

In Fig. 7.15, "

data of Y

3x

that have been reduced from Kerr ellip-

sometry measurements by Wittekoek et al. [22] are reproduced for x D 0 and 0.25.

If the x D 0 (YIG) curve is treated as a base line, the curve for the Bi contribution is

found by subtraction of the two curves. Figure7.16 presents the results of the same

procedure applied to the corresponding "

data. In both cases, the resultant curves

reveal smooth Lorentzian-type functions of ! depicting behavior that is strongly

suggestive of two or three individual transition bands below 4 eV. Equation (7.40)

can be applied directly to the difference curves of Figs. 7.15 and 7.16 by selecting

appropriate values of parameters ,  ,andf for two principal diamagnetic tran-

sitions of opposite sign (the sign is determined by the direction of the magnetic

moment that couples to the electric vector through spin–orbit coupling). As pre-

sented in Figs.7.17 and 7.18, close ﬁts to the experimentally derived curve are made

with transitions at 2.6 and 3.15 eV over most of the range of measurement. To re-

ﬁne the interpretation and extend the model beyond 4 eV, a third transition of similar

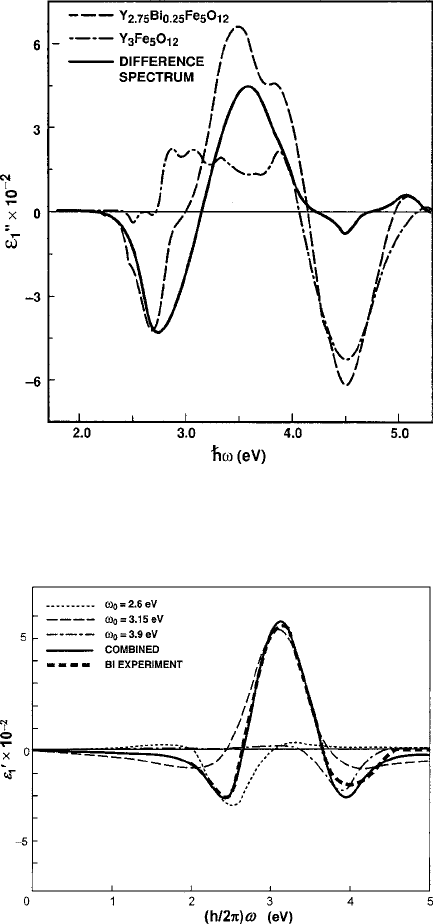
368 7 Magneto-Optical Properties

Fig. 7.16 Y

3x

data of Wittekoek et al. [21], showing the difference curve formed

from the subtraction of the x D 0 and 0.25 curves. Figure reprinted from [25] with permission.

 1993 by the American Institute of Physics

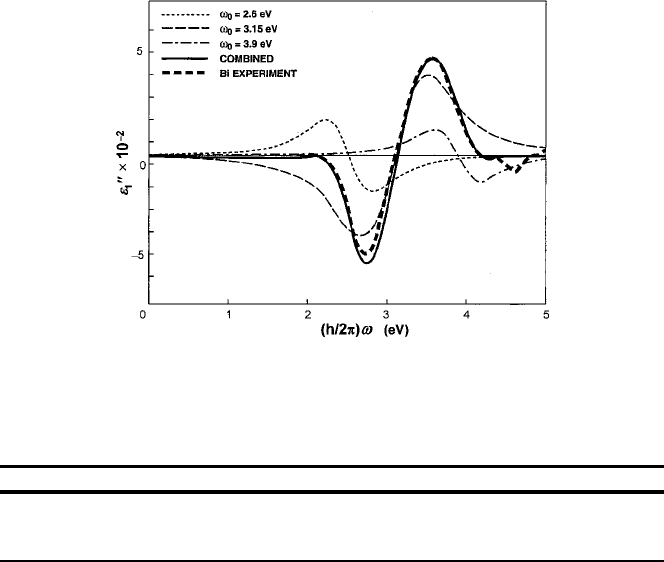
Fig. 7.17 Curves of "

calculated from the parameter values listed in Table. 7.3 showing the com-

bined curve of the Bi effect between energies of 0 and 5 eV. Difference curve from Fig. 7.15 is

added for comparison. Figure reprinted from [25] with permission.

 1993 by the American In-

stitute of Physics

7.3 Magneto-Optical Spectra 369

Fig. 7.18 Curves of "

calculated from the parameter values listed in Table. 7.3 showing the com-

bined curve of the Bi effect between energies of 0 and 5 eV. Difference curve from Fig. 7.16 is

added for comparison. Figure reprinted from [25] with permission.

 1993 by the American In-

stitute of Physics

Table 7.3 Spectral parameters of "

enhancement for x D 0:25

Lattice site !





=

Tetrahedral 2.6 2:8 0.44 0.11 0.25

Octahedral 3.15 8 0.54 0.27 0.5

Tetrahedral

3.9 3 0.44 0.11 0.25

This transition appears to be of tetrahedral Fe origin but may also be inﬂuenced by charge transfer

excitations (which may not be Lorentzian) or by the strong Bi

S !

P transition at 4.5eV [34]

sign and proportions to the one at 2.6 eV is added at 3.9 eV. It is also important to

recognize that the unique spectral shapes of both "

and "

are ﬁtted with the same

set of parameter values listed in Table 7.3.

To highlight further the closeness of the ﬁt between theory and experiment in the

lower energy region, the calculated curve for "

from Fig. 7.16 was modiﬁed accord-

ingto(7.41), scaled to x D 0:44 (with the assumption that the 

dependence on

Bi content remains linear at small values of x)[17] and plotted in Fig. 7.19 together

with the corresponding 

measured curve of Simsa et al. [32] after subtraction of

the Y

baseline. The close agreement over the range from 1 to 2.5 eV indi-

cates that the principal Bi contributions are not of paramagnetic origin.

The opportunity to separate opposing magnetic sublattice contributions by the

signs of the different Faraday peaks is an important aspect of magneto-optical spec-

tra. Scott et al. [27] concluded that the 3.15-eV line originates in the octahedral

Fe–O

complexes (transitions from

S to excited

G or

D bands [33]). From

Fig. 7.16, therefore, one concludes that the weaker 2.6-eV peak is of tetrahedral ori-

gin .Fe–O

/. Most signiﬁcant for practical matters is the dominance of the negative

tail of the intense 3.15-eV line in the 1–2-eV region.

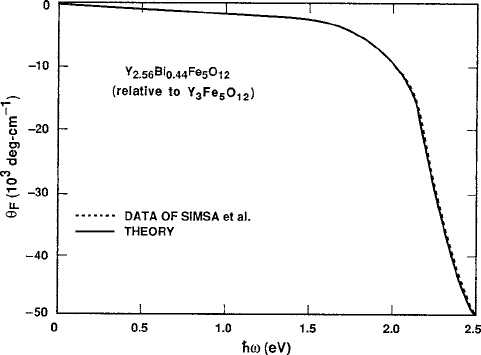
370 7 Magneto-Optical Properties

Fig. 7.19 Comparison between theory (scaled to x D 0:44) and experiment for energies below

2.5 eV, using parameter values of Table. 7.3 Data curve is from [32] and has also been corrected

to remove Y

baseline. For ﬁxed N , the largest reasonable = values below saturation

levels [17] were chosen to ﬁt the data. Figure reprinted from [25] with permission.

 1993 by the

American Institute of Physics

As listed in Table7.3,the values for each transition are broad (0.25–0.5eV).

If the "

values reported [21] are not greatly increased by Bi additions, the large

enhancement of "

would not be caused by an increased f . For the same reason,

the proposition that Bi

transitions cause the "

anomalies would also have to

be ruled out. For a homogeneous distribution, one explanation could be that Bi

ions perturb and enhance the multiplet splitting of the excited band [29]ofthe

exchange-coupled Fe

lattices in direct proportion to the density and strength of

the Fe

–O

2

–Bi

bond linkages, thereby producing (to a ﬁrst approximation) a

linear growth in the product N with x, and a corresponding enhancement of "

for selected Fe

transitions. This situation would be analogous to the increase of

ferrimagnetic resonance linewidths caused by homogeneous distributions of fast-

relaxing ions. As a result, the intensities of the calculated lines were ﬁtted by

selecting appropriate  values, which proved to be larger than reported earlier [21].

Reported saturation of the "

peak at 3.15 eV as x ! 2 may be explained by

the ratio = ! 1. This result further suggests that approximations based on the

=  1 assumption should be avoided in the interpretation of the Bi effects. It

should be pointed out, however, that the "

value at ﬁxed energies in the negative

tails may not saturate because the smaller reverse peaks are moved to lower and

higher energies, as illustrated in Allen and Dionne [17]. This latter feature would

prove beneﬁcial for applications that require materials with the highest 

value at

lower energies.

The magneto-optical effects at 4 eV and above are less easy to interpret because

of the complexity of the excited overlapping bands and the threshold for charge

7.3 Magneto-Optical Spectra 371

transfer between Fe–O

and Fe–O

sites, as well as possible contributions from

the Bi–O

dodecahedral-site transition at 4.5 eV [34]. Because the key transitions

are diamagnetic, meaning that the required orbital splitting occurs in a degenerate

excited P state, the construction of a simple molecular-orbital model is a logical

next step [26].

For ferrimagnets with exchange coupled Fe

3C 6

S ground states, polarization ro-

tation of a wave propagating parallel to the magnetization vector (z direction) is

described mathematically as a frequency-dependentoff-diagonal element of the per-

mittivity tensor. This requires interaction between the electric vector of the optical

wave and the orbital angular momentum L of the excited state. For the mag-

netic moments to inﬂuence nonreciprocal effects, therefore, spin–orbit coupling

is a necessary component. Since the excited-state splitting is the result of spin–

orbit multiplet structure, contributions from the large Bi

spin–orbit interaction

reﬂected through covalent molecular-orbital (MO) states become the focus of this

discussion.

7.3.4 Fe

–Bi

Hybrid Excited States

For ferrimagnets with superexchange coupled Fe

3C 6

S ground states, polarization

rotation of a wave propagating parallel to the magnetization vector (z direction) is

described mathematically as a frequency-dependentoff-diagonal element of the per-

mittivity tensor. This requires interaction between the electric vector of the optical

wave and the orbital angular momentum L of the excited state. For the mag-

netic moments to inﬂuence nonreciprocal effects, therefore, spin–orbit coupling

is a necessary component. Since the excited-state splitting is the result of spin–

orbit multiplet structure, contributions from the large Bi

spin–orbit interaction

reﬂected through covalent molecular-orbital (MO) states is the focus of this discus-

sion. The analysis that follows is based on previous work [26], but has been updated

and employs nomenclature and sign conventions in closer conformance with the

present text.

For a generic two-level system, the method developed in Chap. 2 can be readily

adopted. The secular determinant is given by

 EbE

b  E E

 E

D 0 (7.42)

where b  .E

C E

/ is the transfer integral and  is the overlap integral. Solu-

tion of (7.42) yields the following eigenvalues

C E

/.1 2

/ ˙

 E

.1  

/ C b

2.1 

(7.43)