Dionne G.F. Magnetic Oxides

Подождите немного. Документ загружается.

352 7 Magneto-Optical Properties

7.2 Combined Permeability and Permittivity

As the frontier of signal propagation moved toward shorter wavelengths with the

advent of the ﬁber-optical communications technology, the quest for nonreciprocal

devices in the wavelength band near 1m became a priority for laser source pro-

tection and related applications. Regrettably, the elegance of the microwave band

solution that involved simple magnetic-dipole transitions in conventional ferromag-

netic media could not be extended to the higher energies because of the magnetic

ﬁeld strengths required are prohibitively large. Moreover, although the classical Lar-

mor precession gyromagnetic effect could still be valid conceptually, its value as a

computational tool gives way to a quantum mechanical approach based on atomic

spectra. From a phenomenological standpoint, it is important to recognize that the

propagation theory introduced in Chap. 6 is only part of the reality that now includes

polarization-sensitive electrical permittivity that is variable with frequency. To this

end, the classical models of permeability and permittivity are examined jointly [3].

7.2.1 The ["] [] Tensor Solutions

For an insulating medium of tensor permeability Œ and permittivity Œ" transmit-

ting an rf plane-wave



x;y



exp



˙i!t  

p˙



along the z-axis, the relevant

Maxwell equations at a ﬁxed value of z are

rH DŒ"

D i!Œ"E ;

rE DŒ

Di!ŒH ; (7.13)

where the rf subscript has been dropped for convenience. From (7.13) a solution for

the propagation constant can be obtained by eliminating either H or E. As a result,

a generalization of the magnetic ﬁeld case outlined in Appendix 6A of Chap. 6 can

be written with permittivity as a tensor, according to

rrH D !

Œ"  Œ  H ;

rrE D !

Œ  Œ"  E; (7.14)

where the combined tensor for a z-axis directed plane wave can be reduced to

Œ"  Œ D



i"

Ci"







 i

Ci





 C "

 i ."

 C "

/

Ci ."

 C "

/ "

 C "





: (7.15)

7.2 Combined Permeability and Permittivity 353

Advancing to the solution for the propagation constants of the two modes of circular

polarization [11] we obtain



p˙

D







D





Œ."

 C "

/ ˙ ."

 C "

/ : (7.16)

where 

D  ˙ , "

D "

˙ "

, and the square-bracketed factor contains

the scalar eigenvalue solutions of the secular equation derived from (7.15). The

corresponding eigenfunctions are .1=2/



 iH



for the counterrotating right-

hand and left-hand circular polarization (RHCP and LHCP) modes. Note that (7.16)

reduces to the desired results where dichroism from magnetic only or dielectric only

conditions apply, i.e.,



p˙

D





"

D





".˙ / .magnetic interaction/; (7.17a)



p˙

D





"

D





."

˙ "

/.dielectric interaction/; (7.17b)

where  D 

 i

,  D 

 i

, and correspondingly we deﬁne "

D "

 i"

and "

D "

 i"

7.2.2 Propagation Parameters and Faraday Rotation

The above relation between propagation constant and the combined permeability

and permittivity can be used to generate a more universal expression for the non-

reciprocal rotation of a linearly polarized vector introduced for the rf plane-wave

case in Sect. 6.4. In addition to restoring the dispersive contributions of ", the effect

of magnetic loss embodied in the imaginary parts of  and  can also be included.

Equation (7.16) expressed in terms of the propagation constants becomes



p˙

C iˇ

p˙



D







; (7.18)

from which

p˙

 ˇ

p˙

D







2˛

p˙







(7.19)

In many cases, these complex permittivity parameters are deﬁned with a positive sign.

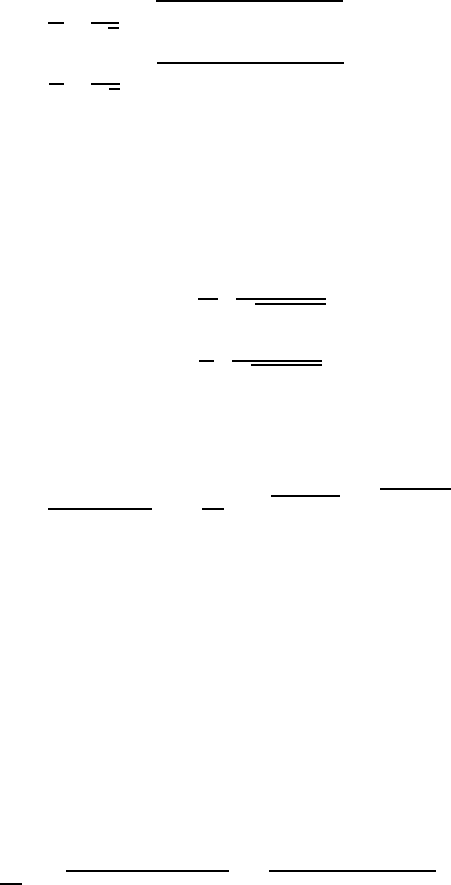
354 7 Magneto-Optical Properties

and

p˙









C ."



002

 ."





1=2

;

p˙









C ."



002

C ."





1=2

: (7.20)

This general expression can be expanded in terms of the  and , "

and "

parameters, each of which contain imaginary terms. For practical situations, the

assumption that the loss terms are small is valid, where !  or  H

,and



=."



 1. By means of binomial expansions, (7.20) can readily

be simpliﬁed to

p˙









;

p˙









; (7.21)

which reduces to (6.118)when"

D 0. As deﬁned previously in (6.122) the Faraday

rotation angle per unit path length can now be expressed as

D '=2 D



p

 ˇ



z 



















z: (7.22)

Where ˛ ¤ 0, the corresponding amplitudes of H

rf

and H

rfC

experience different

amounts of attenuation, which leads to a nonlinear or “elliptical” polarization of the

resultant wave in the magnetized medium.

Applications for the combined theory might be found in the frequency regime

between microwave and optical bands. In the far-infrared regions beyond where

simple microwave Zeeman-type splittings gm

H are limited by applied mag-

netic ﬁelds of only a few Tesla, exchange ﬁelds of 10

–10

T can produce splittings

of much higher energy. The corresponding magnetic transitions can overlap the

electric-dipole transitions of rotational and vibrational molecular spectra. If both

electrical and magnetic contributions overlap in nonabsorptive transmission “win-

dows” at frequencies where the imaginary parts of , , "

,and"

are negligible,

i.e., no near-resonance conditions, (7.22) can be written as







 "

/.

 

/ 

C "

/.

C 



z: (7.23)

By setting the conditions to isolate individual magnetic and electrical propagation

interactions, the inﬂuence of the off-diagonal tensor elements can be readily high-

lighted as

7.3 Magneto-Optical Spectra 355

F



















z: (7.24)

The Faraday rotation angle expressions can be simpliﬁed further if the frequency-

dependent relations for 

and "

are substituted into (7.24). For the magnetic case,

it can be readily shown that 

F

reduces to (6.122)if!

 !

. The dielectric case

can be treated similarly with the relations given in Sect. 7.3.

7.3 Magneto-Optical Spectra

In the energy bands above where average magnetic ﬁelds can create Zeeman split-

tings that allow magnetic-dipole transitions, or where inter-ion spin ﬂips can occur

through magnetoelastic phonon interactions (exchange resonance), the spectra are

referred to as optical rather than electromagnetic and are the result of actual exci-

tations within the orbital angular momentum structure set by the Russell–Saunders

coupling. In the optical bands, the relevant parameters that describe the interaction

between waves and matter are the refractive index n and extinction coefﬁcient k.

Propagation properties are then usually characterized in terms of the complex index

of refraction N D n  ik. For the two circular polarization modes, N

are related

to the propagation constants 

p˙

according to

D







p˙

D ."

˙ "

/ D .n

 ik

D





.˛

C iˇ

(7.25)

Therefore,

 i

p˙





or .ˇ

 i˛/ D





 ik

/: (7.26)

Because the direct magnetic-dipole contributions are negligible in the optical fre-

quency bands, it will be assumed that  D 1 in the analysis that follows, except for

exchange resonance cases where both can apply. In Appendix 7A, the relations for

complex off diagonal elements are derived for use in the ensuing sections.

7.3.1 Electric-Dipole Transitions

If the dispersion of Œ and Œ" elements occurs in widely separated frequency

regimes, the frequency dependence of the tensors can be analyzed separately,

starting with Œ and then applying the results to Œ" by analogy. For low power

356 7 Magneto-Optical Properties

conditions without damping effects (omitted for simpliﬁcation), the respective

gyromagnetic resonance and nonresonance scalar solutions for the right-hand

RHCP(+) and left-hand LHCP(-) circular polarization permeabilities 

D  ˙ 

at a signal frequency ! are given by [3,11]



D 1 C !



D 1 C

 !

; (7.27)

where !

D H

and !

D 4M, the frequency equivalent of the magnetization.

Note that the (+) mode is dominant at resonance ! D !

, but both functions become

comparable away from resonance. To account for damping effects, a relaxation rate

parameter  is introduced. In spectral terms,  represents the half-linewidth (of-

ten designated as !) of a Lorentzian function. Following the Bloch–Bloembergen

model [12], the lineshape functions are expanded to complex relations by substitu-

tion of .!  i/! !, to yield



 !/  i

 !/

C 

: (7.28)

Transition probabilities for magnetic- and electric-dipole interactions with plane-

wave radiation are explained by quantum mechanical time-dependent perturbation

theory [13–15]. Rotating-dipole diagrams are presented in Fig. 7.5. The parameter

.D 4M/ can be expressed as



„



4Ngm

S D

4N

„

; (7.29)

Fig. 7.5 Rotating angular momentum diagrams: (a) spin angular momentum S precessing at the

Larmor frequency about a z-axis magnetic ﬁeld H, and driven by circularly polarized modes of an

rf ﬁeld H

in x–y plane; magnetic resonance occurs when signal frequency equals the Larmor

precession frequency of the S vector; and (b) split p

x;y

orbital states of a magnetic molecule with

orbital angular momentum L that rotates with the electric ﬁeld E

circular polarization modes in

x–y plane; optical transition frequencies correspond to the particular quantum state energies of the

electric dipoles. Figure reprinted from [3] with permission.

 2005 by the American Institute of

Physics

7.3 Magneto-Optical Spectra 357

where N is the net volume density of magnetic ions and S is the spin of one ion.

For the basic example of a Zeeman split S D 1=2 case (Fig. 7.5a) with an excitation

C1=2

1=2

4N

„





C iS







(7.30)

thereby observing the basic selection rule S

DC1.

With m

a;b

as the electric-dipole moment of the respective a and b quantum orbital

states L

D˙1 of an orbital triplet P term sketched in Fig. 7.5b, for an orbital

singlet

S ground state L

D 0 a parameter !

a;b

is deﬁned analogous to !

from

(7.29)and(7.30)as

a;b

4N

„

a;b

4N

„



˙ iL



x ˙ iy



: (7.31)

From the deﬁnition of Suits [16], the oscillator strength f

a;b



a;b

=„e



a;b

and !

a;b

D 4Nf

a;b

=m!

a;b

,wheree and m is the electron charge

and mass, respectively.

In the optical bands, the basic physics involves transitions between atomic states

with orbital angular momentum splittings caused by spin–orbit coupling. For this

example only one spectral transition pair will be considered. In the magnetic-dipole

case, the off-diagonal element  emerges directly from the solution of the clas-

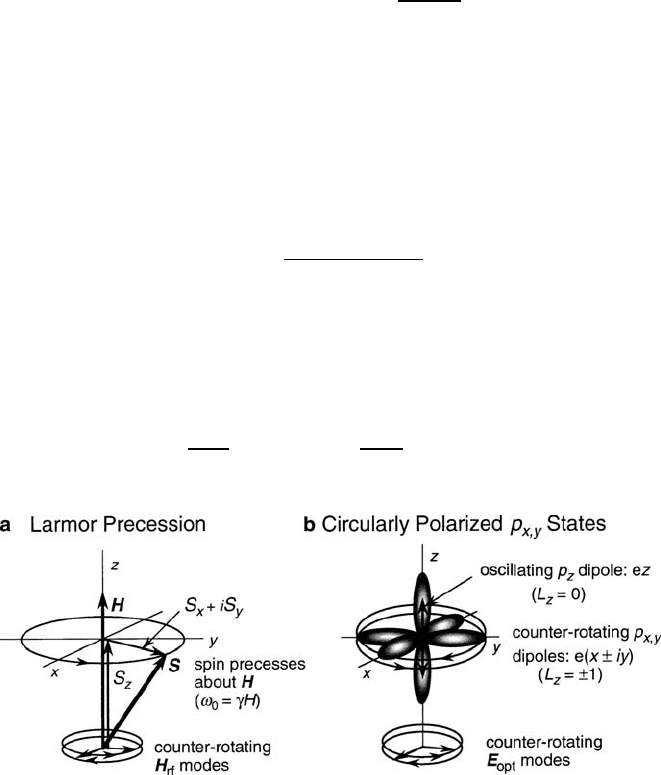
sical Larmor model in the form of a spin-ﬂip transition, as shown in Fig. 7.6a.

Fig. 7.6 Energy level diagrams corresponding to the physical models of (a)and(b). Only the

split excited state (diamagnetic) case of electric-dipole transitions is shown; for the split ground

state (paramagnetic), the levels are inverted. The use of ! to represent quantum energy implies a

suppressed Planck’s constant multiplier „. Note that for the electric-dipole transition the S

D 0

condition is added as a selection rule. Figure reprinted from [3] with permission.

 2005 by the

American Institute of Physics

In this discussion, the symbol N is used instead of n to avoid conﬂict with the index of refraction

n for optical propagation.

358 7 Magneto-Optical Properties

A magnetic ﬁeld creates a frequency splitting !

and determines which circular

polarization mode experiences gyromagnetic resonance and which is unaffected, as

deﬁned by (7.27). By contrast, there are two transition frequencies !

and !

in the

birefringent electric-dipole case, one for each polarization mode. Furthermore, the

selection rules for transitions between angular momentum terms are now L D˙1

(Laporte’s interval rule) and also S D 0.

For separate permittivities from the multiplet splitting, each orbital angular

momentum state interacts with the electric vectors of the both circular polariza-

tion modes, one in resonance and the other in nonresonance, thereby creating four

permittivity functions. The models for the counterrotating electric-dipole moments

that carry the two opposing states of orbital angular momentum .L

D˙1/ corre-

spond to the split levels of the

P orbital quantum term as illustrated in Fig. 7.6b.

Since the lineshape factors are identical for both magnetic- and electric-dipole res-

onances, the relations of (7.27)and(7.28) can be adopted without loss of generality

for each electric-dipole transition to produce the circular polarization permittivities

D "

˙ "

For the dual transitions between L

D˙1 of the

P state and L

D 0 of the

S state, circular mode permittivities corresponding to states labeled a and b are

determined ﬁrst from a modiﬁcation of (7.27)and(7.28):

D 1 C !



C !





D 1 C !



 !



C !



˙ !



: (7.32)

With the aid of (7.32), the tensor elements are obtained from "

D .1=2/

C "



/ and "

D .1=2/ ."

 "



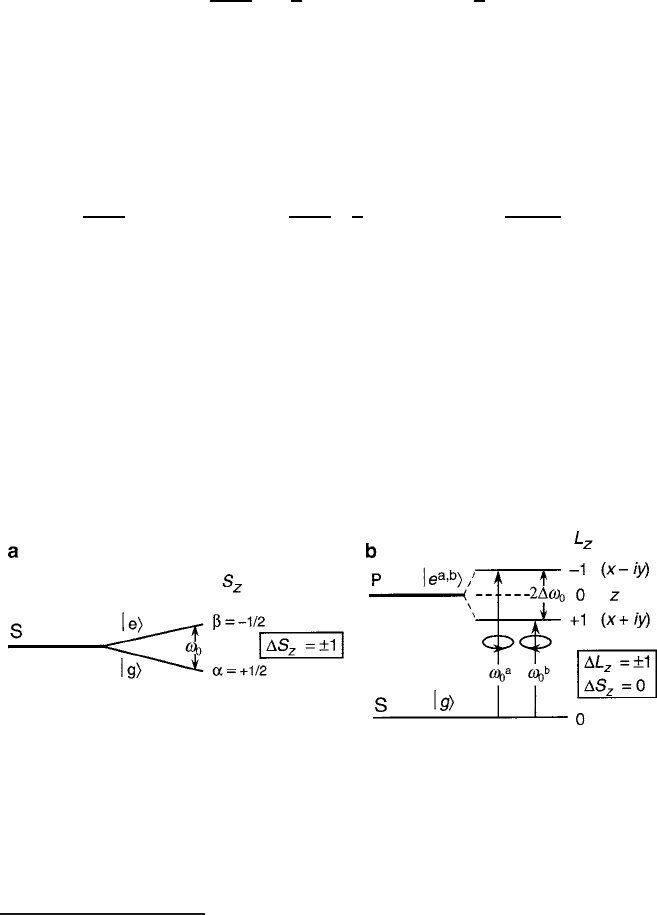
/. For the split excited state of Fig. 7.7a,

Fig. 7.7 Two basic cases for the model transition

S $

P: (a) split excited state (termed diamag-

netic) and (b) split ground state (termed paramagnetic with temperature-dependent populations).

Figure reprinted from [3] with permission.

 2005 by the American Institute of Physics

7.3 Magneto-Optical Spectra 359

Fig. 7.8 Schematic models of "

and "

characteristics as a function of frequency: (a) diamagnetic

transition and (b) paramagnetic transition

D 1 C !



 !/

 

C !/

 



;

D!





 !/

 



C !/

 



; (7.33)

where !

D !

and 2 D !

 !

. As a complement to the diagrams of

Fig. 7.7, the respective curve shapes as a function of ! in the region of resonance

are modeled in Fig. 7.8.

Because the total population density N is shared among the three orbital com-

ponents of the ground state, for an absorptive transition the effective population of

any one level is one-third of the total. The permittivity relations with both resonance

and nonresonance terms for the split ground state (Figs. 7.7band7.8b) case can be

readily derived as

D 1 C



 !/  



 !/

 

C !/  



C !/

 



;

D



  

 !/

 



  

C !/

 



; (7.34)

where !

 .3=2/



C !



and 

D .3=2/



 !



. If the Boltzmann factor

is included to account for the temperature dependence of the populations N

, N

and N

of the split ground state (sketched in Fig. 7.9), the following relation can be

written for the condition that 2  kT ,



D !

1  e

2=kT

1 C e

2=kT

D !

tanh









; (7.35)

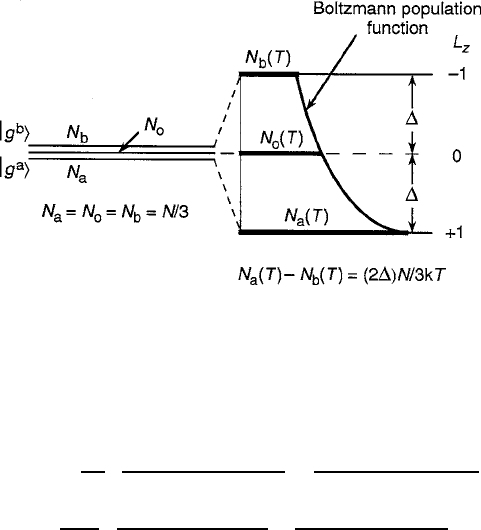
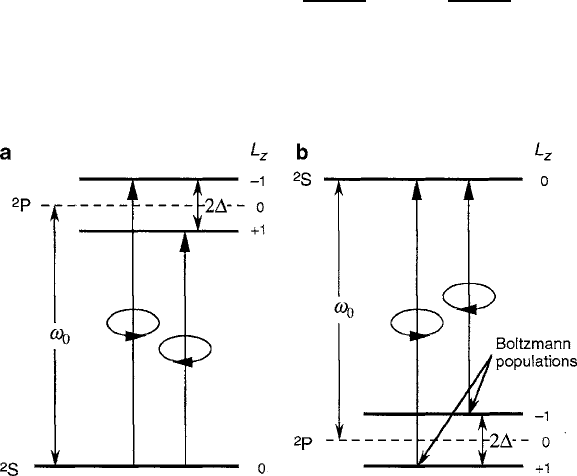
360 7 Magneto-Optical Properties

Fig. 7.9 Temperature dependence of the split ground-state (paramagnetic) case as determined by

a Boltzmann population distribution function. Figure reprinted from [3] with permission.

 2005

by the American Institute of Physics

and the temperature dependence can be introduced to (7.34) according to

D 1 C



 !/  

=kT

 !/

 

C !/  

=kT

C !/

 



D





1  .!

 !/=kT

 !/

 



1  .!

C !/ =kT

C !/

 



: (7.36)

Algebraic sums of selected combinations of the four Lorentzian lineshape functions

can produce the exact "

and "

tensor elements for any electric-dipole transition

with split L D˙1 states. It is important to recognize that the common practice of

omitting the nonresonance term from the these relations can lead to large errors in

the frequency regimes where near-infrared isolators are designed to operate, as dis-

cussed previously[17]. With this approach, these inaccuracies can be easily avoided.

In systems where multiple transition frequencies from different ions occupying dif-

ferent crystal sites, these building blocks can be used with appropriate weighting

of the !

parameter for each !

of the spectrum. For the degenerate ground-state

case, the temperature dependence of the common “paramagnetic” magneto-optical

spectra can be readily inserted into the formalism. Damping effects that produce line

broadening can be added in a straightforward manner at any stage by substituting a

standard relation containing the half linewidth  ,suchas.!  i/! ! [12].

7.3.2 Yttrium Iron Garnet Spectra (Paramagnetic)

The optical and magneto-optical properties of ferrimagnetic yttrium iron garnet

(YIG) were ﬁrst investigated in 1959 by Dillon [18], when a large

Faraday rotation was discovered with the onset of a strong optical absorption at

7.3 Magneto-Optical Spectra 361

photon energies near 2.5 eV. Kahn et al. [19] determined that the magneto-optical

properties were caused by paramagnetic transitions, i.e., g

a;b

ground states, in the

ions. Since the mid-1970s, Scott et al. [20], Wittekoek et al. [21], and Doorman

et al. [22] were able to match many of the identiﬁed magneto-optical lines with

peaks in the various spectra. However, a detailed picture of the quantum structure

necessary to produce the observed birefringent spectra originating from orbital an-

gular momentum L

D˙1 degeneracies in the ground states has proven to be

challenging. The results of a more recent semiempirical ﬁt between permittivity

theory and Kerr-effect measurements by Allen [23, 24] will be summarized.

The diagonal tensor elements "

D "

C i"

are deduced from measurements

of refractive index n and the extinction coefﬁcient k using the standard relation

D .n C ik/

. The off-diagonal elements "

D "

C i"

are calculated from

Kerr ellipticity 

and rotation 

measurements from the relations developed in

Appendix 7A

D 



 3nk

 n



 



 3n

k C k



;

D 



 3n

k C k



C 



 3nk

 n



: (7.37a)

and

 



 n



for small k

 



 n



(7.37b)

Magneto-optical effects occur if the off-diagonal elements "

are non-zero.This

happens when the initial or ﬁnal state of the electric-dipole transition includes a

splitting of an L

stationary states that then ﬁx separate spectral energies for plane

waves of right- and left-handed circular polarization. Expressions for the tensor ele-

ments as a function of angular frequency ! and transition frequency !

are standard

in the literature [19]. As illustrated by Suits [16], a L

D˙1 splitting can occur

in either ground (paramagnetic) or excited (diamagnetic) if an effective

P -state

component is present. The perturbing agent that lifts the L

degeneracy is spin–

orbit coupling L  S . For the paramagnetic case of particular focus here, the split

ground states are thermally populated according to a Boltzmann population dis-

tribution, as discussed in Sect. 7.3.1. Consequently, a difference in the number of

right- and left-handed occupied sites available for selective absorption of circularly

polarized light is established. For the present study, the population ratio of the para-

magnetic case and its relation to the energy splitting 

can be found from the peak

of "

at resonance frequency !

divided by the corresponding optical absorption "



 N



C N



N





2kT

; (7.38)

where N

and N



are the populations of the split ground state in the limit of



 kT . It is easily shown that (7.38) represents the difference of oscillator