Dionne G.F. Magnetic Oxides

Подождите немного. Документ загружается.

412 8 Spin Transport Properties

crystal-ﬁeld distortion caused by a local site deformation or an elastic strain induced

by external stress. In theory, the magnetoelastic (Jahn–Teller) term E

can be

as large as 10

1

if all the distortion energy were coupled into the spin sys-

tem. However, the dependence on spin alignment is more complicated. In general,

paramagnetic and exchange terms account for the respective concave and convex

curves of Fig. 15a. A trace concentration of isolated magnetoelastic ions in sites

with spins stabilized by a spontaneous distortion of the ligands will initially pro-

duce a characteristic paramagnetic tail. In a prestressed condition that occurs from

ﬁlm/substrate mismatches, the strain bias can organize the local site strains into an

energy stabilization that is linearly dependent on spin alignment. With increasing

concentrations, the initial concave shape of the thermomagnetism curve can be off-

set when a cooperative strain begins to form as the individual sites percolate toward

a full magnetostrictive system. The growth of these effects was observed in studies if

Fe was substituted into stoichiometric In

specimens in bulk ceramic form [47].

For signiﬁcant spin alignment at 300 K, the numerator of the exponent must

approach or exceed kT

 200 cm

1

, which occurs in magnetically dense oxides,

e.g., ferrites, where the transfer integrals b can stabilize spin alignment enough

to produce Curie or Neel temperatures of several hundred Kelvin degrees. When

overlap integrals decrease sharply with magnetic dilution, however, breakdown

in long-range spin order begins immediately by spin canting that is discussed

in Chap. 4, and quickly leads to paramagnetism. This is particularly true of com-

pounds based on d

S-state ions Fe

and Mn

for which spin–orbit–lattice

interactions are insigniﬁcant in the nonhybridized ground states.

The contribution of magnetoelastic spin stabilization in dense magnetic oxide

systems is reﬂected in the magnetostriction property, either directly as a coop-

erative strain induced by polarization of spins through spin–orbit coupling into

anetM by an applied ﬁeld, or inversely by the application of external stress

to polarize M . In highly dilute systems, the local site distortions are either dy-

namic Jahn–Teller effects or are largely constrained by the host lattice. Isolated

magnetoelastic ions have Boltzmann spin populations determined by small local

=kT

exponents at room temperature. As the concentration of magnetic ions in-

creases, local dynamic J–T type effects begin to percolate into a net static strain

through intersite lattice interactions that are in turn subject to the Debye temperature

(

 500 K). Because E

is temperature dependent according to the approxima-

tion E

.T / D E

.0/tanh .

=2T

/, which is based on the growth of optical

vibronic phonons from (8.16)for D 1 [42], (7.11) can be reﬁned as

B.T / D tanh



C E

.0/tanh .

=2T

2kT



: (8.25)

As concentrations increase, antiferromagnetic spin pairing will frustrate the net

magnetization. If polarized spin transfer between mixed-valence cations contributes

ferromagnetic double exchange, the parallel spin alignment can survive to higher

8.4 Superconductivity in Oxides 413

concentrations. These magnetoelastic phenomena were modeled semiquantitatively

for Cr

and Fe

C Cu

in In

[42]. In another study, the conﬂict between

magnetoelastic ordering and antiferromagnetic exchange was illustrated for Fe in

SrTiO

where ferromagnetism and strain ordering dominate until antiferromag-

netism appears to take over at Fe concentrations above 40% [48]. In this sense,

ions of the 3d

series such as high-spin 3d

and 3d

could provide both the align-

ment and mobility for spin-polarized conduction at temperatures determined by the

stabilization energy of the overall magnetoelastic system.

8.4 Superconductivity in Oxides

Superconductivity remains one of the most intriguing phenomena in the physical

sciences. In contrast to collective electron metals that have been analyzed success-

fully in momentum space [49], the discovery of HTS in ionic compounds [50, 51]

presents a formidable challenge to the conventional wisdom. With only a few per-

cent of the molecules providing carriers, a “real” space interpretation based on local

effects in the spirit of the London macroscopic molecule seems a logical alterna-

tive approach. The model developed for the transition-metal oxides in the ensuing

discussion is based on the coherent transport of large polarons in lattices with mixed-

valence cations. For purposes of identiﬁcation, it will be referred to as the covalent

electron transfer theory (CET), or simply the large polaron model [8,9]. The ﬁrst re-

quirement is that it conform to the London conditions for superconductivity, which

will be set forth in Sect. 8.4.1.

8.4.1 Classical Foundations

To relate the polaronic transfer mechanism with traditional superconductor phe-

nomenology, it is ﬁrst necessary to review the macroscopic concepts on which any

microscopic theory must be based.

8.4.1.1 The London Equations

Since the electric ﬁeld E D 0 in a hypothetical perfect conductor, it follows that

the magnetic ﬂux density B must be constant to satisfy Faraday’s law rE D

.1=c/ @B=@t. For this reason, such a material would also be described as a perfect

Note that X. Liu, X. Sasaki, and J.K. Furdyna, Phys. Rev. B 67, 205204 (2003) reported strong

inverse magnetostriction effects from dilute concentrations of Mn in the host semiconductor GaAs

at T D 5 K. In a tetrahedral coordination, Mn

(3d

) would offer either J-T or spin-orbit spin

stabilization (Fig. 2.27) sufﬁcient to contribute to the magnetization.

414 8 Spin Transport Properties

magnetic shield. An unchanging value of B, however, is not a sufﬁcient condition

for superconduction, because the Meissner effect requires the expulsion of ﬂux from

the interior of the specimen as it becomes superconducting, i.e., B ! 0.Whenan

external ﬁeld H is removed from a normal conductor that might have attained a

zero resistance state, the existing B would be sustained (ﬂux trapping) by induced

surface eddy currents. It follows, therefore, that a superconductor differs from a

normal “perfect” conductor by the manner in which currents induced by changes in

H are somehow constrained to insure the B D 0 condition.

Since superconducting materials are never spontaneously magnetic, B  H D 0

(i.e., permeability   1), and it follows from the Maxwell equation of magnetic

induction rH D.4=c/ i that the supercurrent density i

is also zero in

the interior, where B D 0. This means that the current must exist only at the

surface, and that the material behaves as a perfect diamagnet, with i

inducing a

ﬁeld exactly equal and opposite to H . It is clear from inspection that Faraday’s law

alone cannot account for the E D B D 0 condition. As a result, the London phe-

nomenological equations [52] were formulated to augment Maxwell’s equations for

superconductors:

E D



4



.@i

=@t/ ; (8.26a)

and

H D



4



ri

; (8.26b)

where the London penetration depth 



=4e



1=2

is a constant inversely

dependent on the carrier density n

, with m and e as the carrier mass and charge,

respectively. For a stationary state, @i

=@t D 0,and(8.26a) fulﬁlls the E D 0

requirement. If (8.26b) is then combined with the Maxwell induction law rH D

.4=c/ i

, the following differential equations emerge, provided that rH D 0

and ri

D 0:

H D H =

;

And

D i

=

: (8.27)

The solutions of (8.27) yield H and i

as exponential functions of distance x

from the specimen surface, e.g., H D H

exp .–x=

/. Therefore, both H and i

are maxima at the surface and decay inward with a proﬁle characterized by London

penetration depth 

, in compliance with the Meissner effect. If ﬂux and current

are expelled from the interior of the material from B D E D 0 conditions, they

coexist in surface layers of depth 

as solenoidal vectors normal to each other, i.e.,

rH D 0, ri

D 0, and may be illustrated by the simple geometries of Fig. 8.16.

Here it is necessary to use the vector identity: r

rv

rv

r

v Dr

v, with

rH D 0 and ri

D 0.

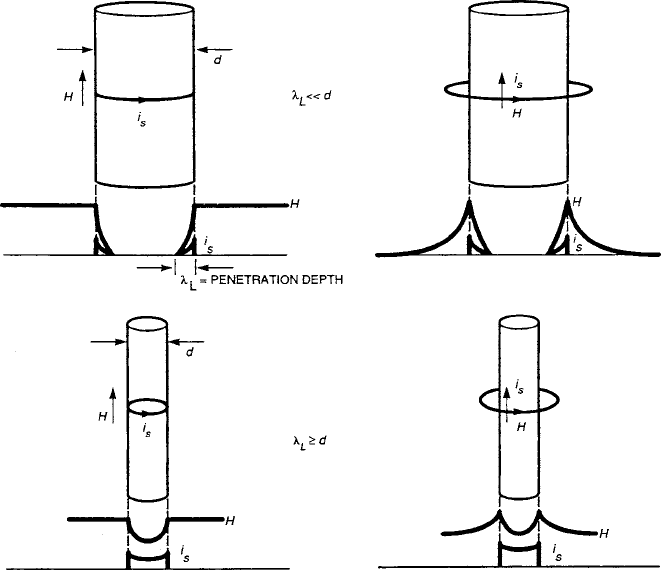
8.4 Superconductivity in Oxides 415

Fig. 8.16 Perpendicular relations between current and magnetic ﬁeld for superconducting cylin-

ders of large and small diameters. In the upper cases, the current responds to an applied external

ﬁeld within a depth 

, and in the lower ones, the ﬁeld is generated to a depth 

by a current

passed through the superconductor. For the thin cylinders where 

 d , the penetration can be

almost complete [9]

A more useful relation is the implied interdependence of i

and H in a super-

conducting environment, where E D 0.SincerH D 0, H may also be deﬁned

in terms of the magnetic vector potential according to H DrA, and it follows

from (8.26b)that

Dc=



4



A D



=mc



A; (8.28)

a relation frequently referred to as the “Ohm’s law” of superconduction. It should be

noted that (8.28) is not gauge invariant, and that a further constraint must be placed

on A for application to speciﬁc phenomena. In the most general case of simply

connected superconductors, the “London” gauge rA D 0 is chosen to conform

to the ri

D 0 condition that deﬁnes the observed supercurrent rigidity, i.e., no

current components normal to surface.

Although superconductors feature zero resistance, to conform to the phenomeno-

logical dictates of the London theory, which concludes that supercurrents are

416 8 Spin Transport Properties

controlled by a magnetic ﬁeld and not an electric ﬁeld, supercurrents are constrained

in paths near the specimen surface in a manner that prevents eddy currents and leads

to internal ﬂux expulsion in external magnetic ﬁelds.

8.4.1.2 The Macroscopic Molecule

A more fundamental derivation of (8.28) may be obtained from classical elec-

trodynamics, where the mean local canonical momentum of individual carriers

hpiDmhviC.e=c/ A, with hvi as the local mean carrier velocity. Since sta-

tistical mechanics dictates that hviD0 in a normal conductor, it follows that

hpiD.e=c/ A in the normal state. For a superconducting ground state, however, a

Bloch theorem [53] concluded that hpiD0, implying a certain rigidity or inabil-

ity of the momentum to respond to H , and therefore that hviD.e=mc/ A.For

a chain of ordered carriers of number density n

, it follows that the supercurrent

density i

D n

ehviD



=mc



A, thereby producing an alternate derivation

of (8.28). For this electrodynamic approach to comply totally with the constraints

of the phenomenological result that ri

D 0, it is not only necessary that the

gauge condition rA D 0 apply, but also that rn

D 0.

Therefore, the basis for

describing the supercurrent as “spatially rigid”, i.e., the hpiD0 condition, must

include the condition that the distribution of carriers be uniform (ordered) along the

current path.

Since the earliest superconductors were metals, the notion of spatially ordered

carriers was not readily applicable to a free-electron gas. A quantum mechanical

extension to this classical concept evolved from the nonlocal ideas of Pippard [54],

i.e., the analogy of supercarrier coherence length 

to normal carrier mean-free-

path, giving rise to the Ginsburg and Landau [55] ensemble-average wavefunction

, which in turn is related to the supercurrent electron density by the standard

expectation-value relation

D n

; (8.29)

where the number density n

now represents the instantaneous probability of a su-

percarrier existing at a position vector r. As a result, (8.26) may be written as

D



=mc



A; (8.30)

with the attendant implication that rj

D 0 to satisfy the condition that rn

D 0.

Four important conclusions may be deduced from this wavefunction rigidity con-

cept (1) the current density vector i

is directly and exclusively controlled by the

magnetic ﬁeld through the vector potential A; (2) the eigenstate of the supercurrent

Recall that ri



=mc



rA C A rn

,andforri

D 0, both rA and rn

D 0.

This latter condition not only is necessary for supercurrent rigidity in the classical argument, but

also is sufﬁcient, since a carrier distribution dynamically ordered in real space is a rigid current by

deﬁnition. In effect, it should be considered the fundamental physical requirement for the applica-

bility of (8.28) to superconductivity.

8.4 Superconductivity in Oxides 417

has the properties of a space-invariant wavefunction with zero average momentum

.hpiDr

D 0/; (3) the resulting spatial invariance of the carrier density n

im-

plies ordered or equispaced supercarriers; and (4) superelectrons cannot be part of

the normal free-electron gas. If the carriers have similar quantum states that may

be described in terms of a single giant molecular-orbital wavefunction, the current

rigidity imposed by the ﬁxed wavefunction provides an immediate explanation for

the absence of eddy currents and the presence of ﬂux trapping in the superconduct-

ing state.

8.4.1.3 Nonlocal Considerations

Similar to the nonlocal range of normal electrons characterized by a mean-free-

path of length `, Pippard [54] proposed that a sphere of radius 

be considered as

a nonlocal region in which each superelectron would exist within the correlation

scheme.

The coherence length 

may be estimated from the uncertainty principal

once a value for momentum p

is determined.

Since wavepackets have a spatial proﬁle, Ginsburg and Landau [55] reasoned that

the coherence length could be readily introduced through a generalized form of

with an exponential decay, and proposed a solution of a Schrodinger-type equation

with

.r/ D

.0/exp .r=/ ; (8.31)

where  is a more generalized coherence length. In this context,  represents the

smallest size of wavepackets that the superconducting charge carriers can form. In

a context more appropriate to the discussions that follow, the gradient of the super-

conduction carrier number density wavefunction may be expressed as

 .2=/

2  .2=/ n

(8.32)

As  !1, rn

! 0 for spatial ordering of carriers. Figure 8.17 presents a rudi-

mentary contrast between the macroscopic molecule and ensemble wavefunction

concepts.

In band-theoretical terms that have been applied to conventional metal super-

conductors, an intrinsic coherence length 

 .h=2/ v

=kT

is deﬁned in term

of the Fermi velocity v

and superconduction critical temperature T

. A more gen-

eral deﬁnition was pointed out by Pippard for materials where the coherence length

is reduced by impurities that limit the electron mean free path `, according to

1=  1=

C 1=`. As a consequence, three classes of superconductors may be

deﬁned (a) type-I pure superconductors with large 

 

that require a full non-

local theory treatment (Pippard superconductors), (b) impure superconductors with



 ` that are controlled by the mean free path (London limit, where <

)and

For normal conduction, ` is the average distance that an electron can be transported without

scattering; for superconduction 

is the distance that a superelectron can remain in coherence with

the ensemble as part of the giant molecular state.

418 8 Spin Transport Properties

Fig. 8.17 Contrast between the classical macroscopic molecule concept and the microscopic

ensemble wavefunction theory in their approaches to satisfy the requirements of the phenomeno-

logical London theory

 

. For class (b) (8.28) is modiﬁed to read

D



=mc



.=

/ A,where

 



; only for class (c) is (8.28) valid as

stated. In practice, classes (b) and (c) are type-II superconductors, the former result-

ing from impurities, and the latter representing the case of small coherence length.

The ratio  D 

=

is effectively a constant with temperature. In physical terms,

the ideal type-I superconductor has features   1,and

!1and 

! 0;in

the opposite extreme, the magnitudes of these quantities reverse,   1,and

! 0

and 

!1in the natural type-II case. The essential point is that the coherence

length represents a measure of the wavefunction uniformity; it is the quantum me-

chanical equivalent of the spatially ordered carrier concept of the classical London

theory, which will be examined further in the context of coherent electron tunneling

in later sections. In magnetic oxides, the conditions necessary to satisfy the London

phenomenological requirements can be satisﬁed in select compositions where large

polarons are formed from charge transfer between mixed-valence transition metal

ions provided that antiferromagnetic spin ordering is frustrated.

8.4.1.4 Carrier Statistics

The microscopic view of superconductivity in metals is that boson carriers are

created from the free electrons with energies near the Fermi level. The result-

ing supercarrrier ensemble comprises “Cooper pairs” that form the basis for the

Bardeen–Cooper–Schrieffer (BCS) microscopic theory of superconductivity [49].

Since the quantum electrodynamic version of the London theory requires that the

carrier ensemble form a single wavefunction





, the individual carriers

8.4 Superconductivity in Oxides 419

cannot be fermions because of the Pauli principle restriction that only one fermion

can occupy a state at one time. Supercurrents would therefore occur as bosons that

condense to form a superﬂuid (boson condensation). In the BCS theory, bosons are

formed from electron (Cooper) pairs with opposite spins in k-space mediated by

lattice vibrational modes (phonons), so that the particles or carriers have a double

electron charge and zero spin quantum number .S D 0/. If a chain of uniformly

spaced polaron carriers move in real space as a dynamic ferroelectric condensation,

there need not be competition for quantum states. Carriers enter cells to occupy

states vacated by simultaneously exiting carriers. This situation is analogous to a

vacuum diode without space charge, where each electron emitted from the cathode

arrives at the anode before the next one is emitted.

Since the large polaron model is based on the classical London theory (rn

 0

instead of rj

 0), the carriers are not assumed to be free electrons, and there

is no requirement for paired electrons mediated by phonons or other “entities” in

k-space; in fact, there is no requirement for paired electrons based on purely elec-

trostatic grounds. Instead, the individual polarons may be ordered electrostatically

by repulsion within a chain of covalent bonds (the giant molecule concept), and real-

space spin pairing in a supercurrent could be required only to maintain any existing

dynamic antiferromagnetic order (e.g., spin waves) along the molecular transfer

paths. The Pauli principle is satisﬁed if either the polaron spin S

D 0 and magnetic

disorder prevails in a lattice that favors antiferromagnetic coupling in an undiluted

state, or the host-lattice ion spins S

themselves are zero. Where the carriers trans-

fer as real-space pairs with the double electron transfer of an S

D 0 polaron, the

single ensemble wavefunction solution of Ginsburg and Landau becomes applica-

ble since the limitations of Fermi statistics are circumvented by S D 0 bosons.

Since these bosons are local and would condense in real space, the overlapping ne-

cessitated by the k-space Cooper pair correlation is no longer of concern, and the

question of a Schafroth condensation

is moot. Bose–Einstein statistics could also

apply as in the quantum boson ﬂuid formalism required by the BCS theory. Whether

as individuals or pairs, however, covalent rather than conduction electrons are in-

volved, and the superconduction system proposed is more localized than collective,

particularly in the systems of low polaron density.

8.4.2 Zero-Spin Polarons and Magnetic Frustration

Superconductivity occurs in oxides where spin alignment and rS D 0 issues are

moot if the spin of one of the transfer cations is zero and the lattice environment

is without long-range antiferromagnetic order. In this case polaron tunneling is the

dominant transfer mechanism because the b

hop

condition is assured and inco-

herent thermal hopping is reduced to a secondary role at low temperatures [7]. Spin

transport in transition-metal oxides in which signiﬁcant local magnetic exchange

See, for example, J.M. Blatt [56].

420 8 Spin Transport Properties

energy is present can also occur in select situations where the minority transfer ion is

in a zero-spin state .S D 0/. A remarkable feature of this situation is seen in p-type





–O

2

Cu



, low-spin) and n-type Cu





–O

2

Cu





conﬁgurations, also in 180

bonds of the perovskite structure. For the Cu

ion,

the S D 0 state arises from a low-spin d

conﬁguration in the e

shellthatoc-

curs because of a large splitting of the e

doublet ﬁrst reported in .LaSr/ Cu

[57], the upper d

y

orbital empty and available to accept a transferred spin. It

should be noted that this arrangement dictates a two-dimensional property and dif-

fers from the charge-transfer situation in the manganites, which can occur in either

orbital, depending on the sign of the crystal-ﬁeld distortion. Here the splitting of

y

and d

exists naturally as a result of the tetragonal/orthorhombicsymmetry

.c=a; b > 3/ of the layered-type of perovskites and not necessarily from a J–T effect

required to create the e

splitting in the cubic or rhombohedral manganites [32].

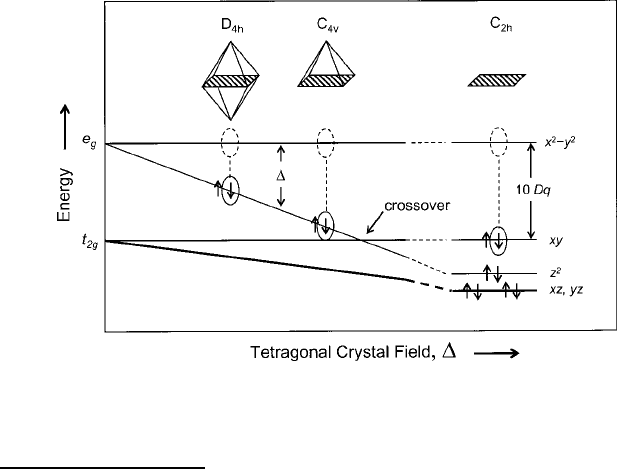
The dependence of this effect on the degree of tetragonal distortion of the crys-

tal ﬁeld as it evolves from a c-axis extension to the formation of a pyramid and

ﬁnally to a planar ligand arrangement is diagrammed in Fig. 8.18. Unlike the case

where ferromagnetism induced as a byproduct of spin-polarized electron transfer

in the Mn

3C.4C/

combinations eliminates the exchange contribution E

hop

to the ac-

tivation energy, the involvement of S D 0 ions removes the internal polarization

exchange energy and therefore renders moot any Hund’s rule considerations. In ad-

dition, charge transfer from these mobile nonmagnetic ions causes local breakdowns

Fig. 8.18 Growth of e

doublet splitting and stabilization of the d

low-spin state as the tetragonal

crystal ﬁeld component increases from z-axis distorted octahedron

to pyramidal

planar

[9]

A Jahn–Teller condensation in the other end member La

was proposed when an increase

in the c=a ratio from 3.30 to 3.46 correlated with antiferromagnetic ordering of the Cu

J–T ions

(J.M. Longo and P.M. Racah, J. Solid State Chem. 6, 526 (1973).

8.4 Superconductivity in Oxides 421

of the antiferromagnetic couplings and can eventually reduce the N´eel temperature

to zero by causing the spin alignment frustration to spread throughout the entire

lattice [23,58].

The mixed-valence manganites and cuprates are both metallic if the hopping

activation energy contribution from antiferromagnetic exchange is compromised.

1x

MnO

is metallic for x<0:5because of the unusual occurrence of fer-

romagnetism. However, a net spontaneous magnetic moment represents an internal

source of magnetic ﬂux that depresses superconductivity. The existence of a spon-

taneous magnetic moment, however, eliminates the possibility of superconductivity.

2x

CuO

and other high-T

cuprates are metallic because the zero-spin Cu

ions preclude any type of exchange trap, and thereby frustrate antiferromagnetic

order.

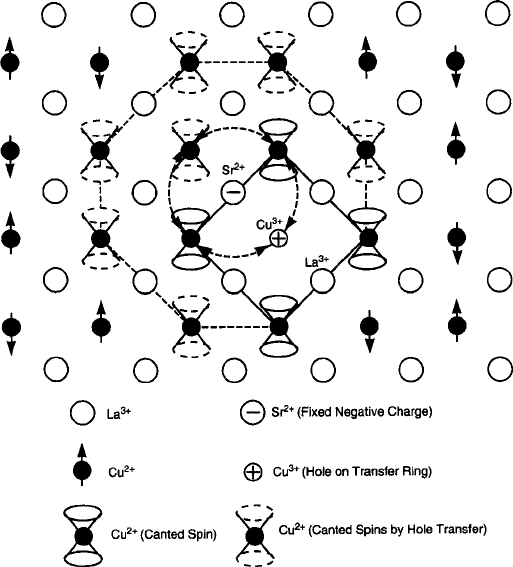
As sketched in Fig. 8.19, the polaronic hole carriers created by zero-spin Cu

ions of concentration x < 0:08 in La

2x

CuO

would be more than sufﬁcient

to disrupt the antiferromagnetic order among the sites immediately surrounding the

Fig. 8.19 Origin of antiferromagnetic frustration caused by zero-spin Cu

ions in La

2x

CuO

. Breakdown in ordering can occur with only one out of 12

x  0:08

S D 0 sites in

the Cu

sublattice in the region surrounding an Sr

“impurity” that acts as a ﬁxed negative

charge. Note that the Cu

hole can transfer around the inner ring in the manner of the model in

Fig. 8.2, carrying the canted spins of its four Cu

neighbors with it [9]