Dionne G.F. Magnetic Oxides

Подождите немного. Документ загружается.

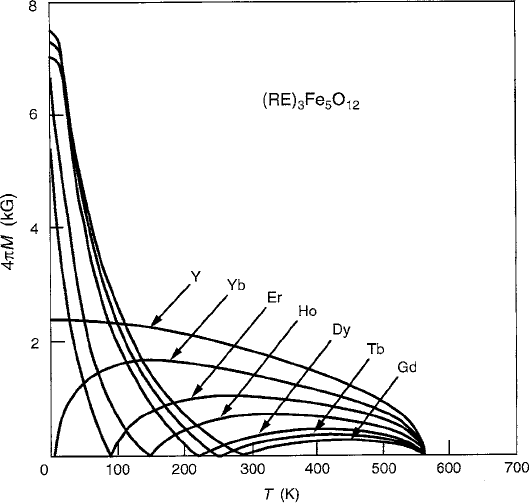
180 4 Ferrimagnetism

4.3.3 Rare-Earth Garnet Ferrites

When rare-earth ions with unﬁlled 4f

shell are substituted into the c sublattice

to form solid solutions of .RE/

and Y

, the magnetic properties

of the iron garnets take on a remarkably different character. The earliest studies

on the magnetization behavior of this family were reported by Bertaut and Pau-

thenet [50,51] whose data are replotted in Fig. 4.16 for the series from Gd

to Yb

, with Y

included as a diamagnetic reference ion in the c sites.

The most distinctive feature of these curves is the magnetization reversal that takes

place at a compensation temperature. This occurs when the magnetic moment of

the c sublattice equals and then surpasses the net moments of the opposing d and

a sublattices, causing M

to switch its alignment from M

to M

in the simple

three-ion model of Fig. 4.17, according to

M D

 M

/  M

: (4.29)

To explain this effect analytically, the N´eel theory must be expanded to three or more

sublattices with the number of molecular ﬁeld coefﬁcients increasing from four to

nine or more, according to

Fig. 4.16 Thermomagnetism curves of the rare-earth series occupying c sites in the iron garnet

system

. Curves are replotted from data of Bertaut and Pauthenet [50]

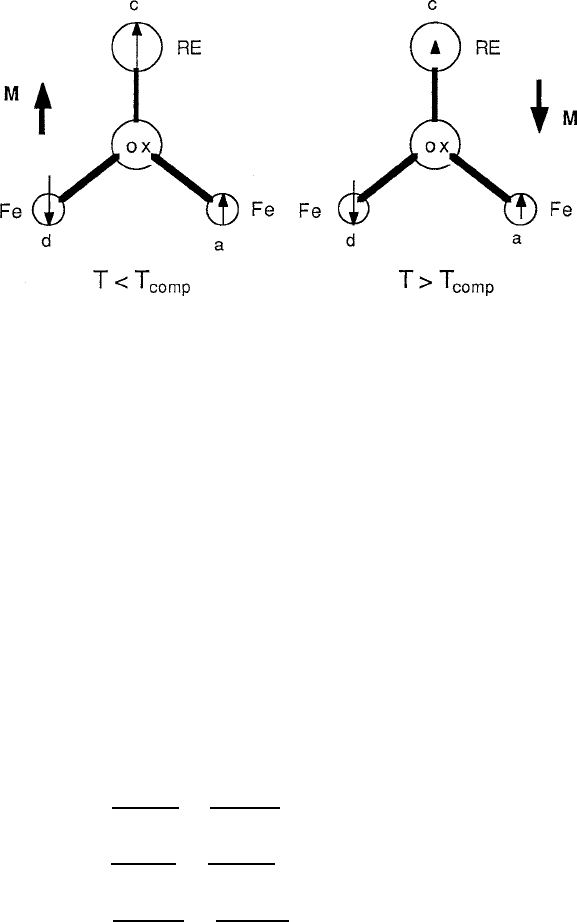
4.3 Ferrimagnetic Oxides 181

Fig. 4.17 The anatomy of the sublattice magnetic moment cancellation that causes the compen-

sation temperature in rare-earth iron garnets

.T / D M

.0/ B

.T / D M

.0/ B

/; (4.30)

.T / D M

.0/ B

where

.0/ D 3g

.1  k

.0/ D 2g

.1  k

/; (4.31)

.0/ D 3g

.1  k

The complete expressions for the Boltzmann energy ratios are given by

.T / D

.a/

ŒN

C N

;

.T / D

.c/

ŒN

C N

; (4.32)

.T / D

.d /

ŒN

C N

:

Figure4.18 illustrates the thermomagnetic contribution of the rare-earth ions from

the c sites, which are seen to exchange couple only to the a and d sites and not to

each other.

In the relations involving the c sublattice, the magnetic moment is deter-

mined by the total angular momentum J

instead of only the spin component S

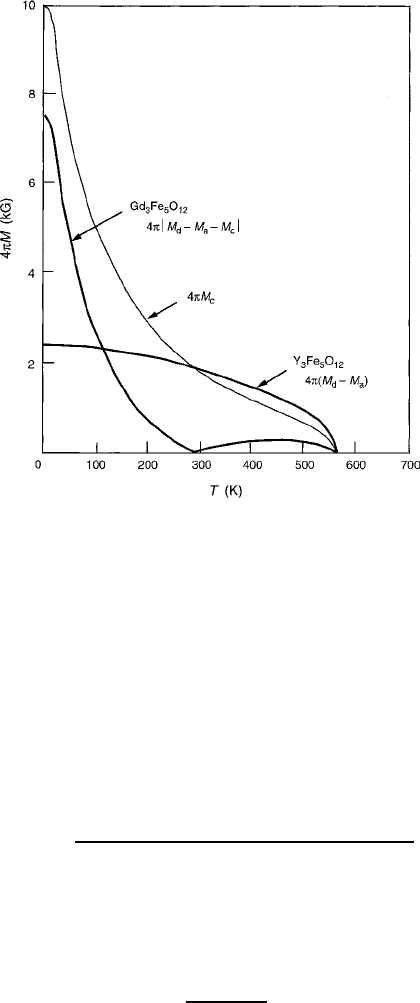
182 4 Ferrimagnetism

Fig. 4.18 Thermomagnetism curves of gadolinium-iron garnet

and yttrium-iron gar-

net

, showing the contribution of the Gd

sublattice and indicating the formation of

the compensation temperature T

comp

. The curve for the Gd sublattice was obtained by a simple

arithmetic subtraction, which is not strictly accurate but adequate for illustrative purposes

Because the rare-earth ions of the c sublattice have the unpaired spins in the 4f

shell, the orbital angular momentum is largely unquenched by the crystal ﬁeld,

as discussed in Sect. 2.3. Unlike the 3d

series where the crystal ﬁeld strength

10Dq  1 eV, the crystal ﬁelds to which the unpaired 4f electrons are exposed are

only 10

2



100 cm

1



. This means that the vector sum J

remains a “good”

quantum number. For this reason, it must be used in the expression for the magnetic

moment of the c sublattice, and also in the expression for g

basedon(1.19)

D 1 C

C 1/ C S

C 1/  L

C 1/

: (4.33)

For the rare-earth ions of the upper half of the 4f

series (heavy rare earths, n>7),

the Russell-Saunders coupling scheme for the multiplet structure dictates that the

ground state J

C S

and (4.33) conveniently reduces to

C 2S

C S

: (4.34)

4.3 Ferrimagnetic Oxides 183

It is instructive to point out that while the L

and S

vectors are collinear for

the heavy rare-earth ions, they oppose each other in the lighter .n < 7/ ions, with

 S

according to the required multiplet ordering. Because it is only

that must align antiparallel with the superexchange-coupled sublattices, L

will

automatically tend to be parallel to the neighboring spins, thereby reversing the

alignment of J

to S

and S

,ifL

. In other words, the sign of M

(4.31) will change to positive. Since this condition always applies in the rare-earth

group, we can substitute J

 S

into (4.33) to obtain

 2S

C 1

 S

C 1

: (4.35)

Equations (4.33)–(4.35) apply well to the rare-earth series, but have no validity

in the 3d

group because of the breakdown in Russell-Saunders coupling due to

crystal ﬁeld lifting the L

degeneracy. This topic will be discussed in Chap. 5.

The fact that S

alone interacts with the exchange ﬁelds raises a conceptual

question when J

is introduced to M

in the molecular ﬁeld terms N

, N

and N

. If the model is formulated to maintain the spin-only rigor [52], the

coefﬁcients will scale to larger values by the ratio of J

in order to be consistent

with the relations of (4.32). For academic interest, a spin-only version of the above

model is outlined in Appendix 4C.

The earliest attempt to determine the molecular ﬁeld coefﬁcients for the rare-

earth series was reported by Al´eonard from reduction of paramagnetic suscep-

tibility data above the Curie temperature [53] employing the method described

in Sect. 4.1.2. Although efforts to apply these results to ﬁt the magnetization vs.

temperature measurement data below the Curie temperature were unsuccessful,

Al´eonard’s values served as useful starting points for Dionne’s solution [22, 54]

that was carried out in the manner described previously for diluting the Y

host system. In Table 4.7 molecular ﬁeld values are listed, including a set reported

by Brandle and Blank [55] who also used the approach of Dionne.

At the lowest temperatures, there remains a controversy in the initial .T D 0 K/

magnetization of Tm

and to a lesser extent that of Yb

. Because

the steepness of the slope of M

vs. T could have allowed the overlooking of

compensation points very close to the lowest measurement temperature of 4.2 K,

misinterpretation of the data is a distinct possibility. This problem is illustrated in

thedataFig.4.19. The issue is whether the c-sublattice contribution to the mea-

sured M is parallel or antiparallel to M

,i.e.,whetherM

takes a positive or

negative value in (4.29). A summary of molecular ﬁeld coefﬁcients derived from

various values of M

for Tm

, including a proposed case that might ﬁt if

the measurements were extended down to T D 0 K. A similar effort is made for

. For a more comprehensive discussion of this question the reader again

is directed to the review article by Geller [15]. This subject will be continued in the

next section as part of the analysis of another peculiar effect.

184 4 Ferrimagnetism

Table 4.7 Molecular ﬁeld coefﬁcients of rare-earth ions in garnet ferrites



Dionne [54] Brandle-Blank [55]Al´eonard [53]

Ion N

6.00 3:44 3.40 1:20 ––

6.50 4:20 4.60 4:40 3.40 1:80

6.00 4:00 3.60 3:20 3.95 3:35

4.00 2:10 2.40 4:00 1.50 0:75

2.20 0:20 1.00 0:60 1.25 0:75

3C b

17.0 1:00 – – 8.00 1:00

3C c

10.4 0:61 –– ––

3C d

9.2 0:54 –– ––

3C e

6.1 0:36 –– ––

3C b

8.0 4:00 8.80 1:00 2.00 1:70

3C e

6.8 3:4 –– ––



All coefﬁcients are expressed in units of mol=cm

Derived from paramagnetic susceptibility measurements [53]

Dionne values based on data of Geller et al. [56]; Al´eonard values were reduced from his own

data [53]

Dionne values based on reinterpretation of data of Geller et al. [56]

Dionne values based on data of Bertaut and Pauthenet [50]

Proposed values; see footnotes to Table 4.8

Fig. 4.19 Details thermomagnetism curves of Lu, Tm, and Yb iron garnet systems below

T D300 K. Dashed curves indicate alternative interpretations. Data are from Geller [15]

4.3.4 Rare-Earth Canting Effect

Before leaving this topic, we must pay attention to an important effect that emerges

from the analysis of the rare-earth magnetic garnets. As can be noted in the J

column of Table 4.8, Dionne’s original reduction of Geller et al. data [56] indicates

values of the total angular momentum that are less than the nominal rare earth

4.3 Ferrimagnetic Oxides 185

Table 4.8 Rare-earth ion angular momentum in garnet ferrites (based on data at T D 4:2K)

Ion L



deg:

g

0 3.5 3.5 2 3.5 1.0 0 – 2.0 3.5

3 3 6 3/2 4.6 0.84 40.0 0.32 1.73 4.0

5 2.5 7.5 4/3 5.3 0.71 45.0 0.41 1.54 4.6

6 2 8 5/4 5.0 0.62 51.5 0.37 1.49 4.2

6 1.5 7.5 6/5 4.6 0.61 52.0 0.42 1.38 4.0

3C a

5 1 6 7/6 1.1 0.18 79.6 – – –

3C b

5 1 6 7/6 1.77 0.30 72.5 0.01 1.95 1.06

3C c

5 1 6 7/6 2.0 0.33 70.7 0.07 1.75 1.33

3C d

5 1 6 7/6 3.0 0.50 60.0 0.30 1.40 2.5

3C e

3 0.5 3.5 8/7 1.5 0.43 64.8 0.24 1.42 1.21

3C f

3 0.5 3.5 8/7 1.75 0.50 60.0 0.33 1.33 1.5

Va lues b as ed o n n

D 1:2 from data of Geller et al. [56]; This moment assumes no compensation

point. Corresponding g

, J

,andL

values were interpreted as negative or unrealistic, suggesting

a possible misjudgment in the reduction of the data

Va lues bas ed on n

D1:2 from reinterpretation of Geller et al. data. In this case the same M

value is used but a compensation point is assumed

Va lues b as ed o n n

D2, deduced by Bertaut and Pauthenet [50]

Proposed values based on n

D –5 at T D 0 K to provide better ﬁt to the monotonic trends

Va lues b as ed o n n

0 from data of Geller et al. [56]

Proposed values based on n

D –3 at T D 0 K to provide better ﬁt to the monotonic trends

free-ion values, i.e., J

< L

C S

. For a decrease to be realized in the effec-

tive value of J

in the iron garnet lattice, orbital degeneracy would be lifted through

direct coupling of the 4f lobes to the 2p orbitals of the oxygen ligands and the 3d

lobes of the Fe

ions in the d and a sites. The net result of these interactions would

provide a crystal ﬁeld and molecular orbital stabilization of the ground J

term suf-

ﬁcient to partially quench the orbital magnetic moment, as described in Sect. 2.3.

We consider two ways to view this phenomenon: (1) semiclassically with the

magnetic moments associated with the rare-earth ions M

D g

simply

canted as in the case of iron spins in diluted sublattices described previously in

Sect. 4.2 where the canting is characterized by cos  D J

, and (2) quantum

mechanically with the orbital angular momentum partially quenched, leaving a re-

duced orbital component L

, such that J

D L

C S

In the semiclassical case, we assume that the orbital angular momentum is not

quenched because spin-orbit coupling is the dominant interaction. The canting of J

will then be determined by the relative strengths of the exchange interaction between

with the net spin moment of the iron sublattices and the Stark coupling between

and the c-site crystal ﬁeld. In the model diagrammed in Fig. 4.20, the exchange

ﬁeld H

competes with the crystal ﬁeld vector E

(assumed to be orthogonal

to H

for illustrative purposes) for the J

vector. Stabilization of the combined

energies as a function of canting angle  is related by

E./D eE

 L

C g

 H

C g

 H (4.36)

D eE

sin C g

C J

H/cos ;

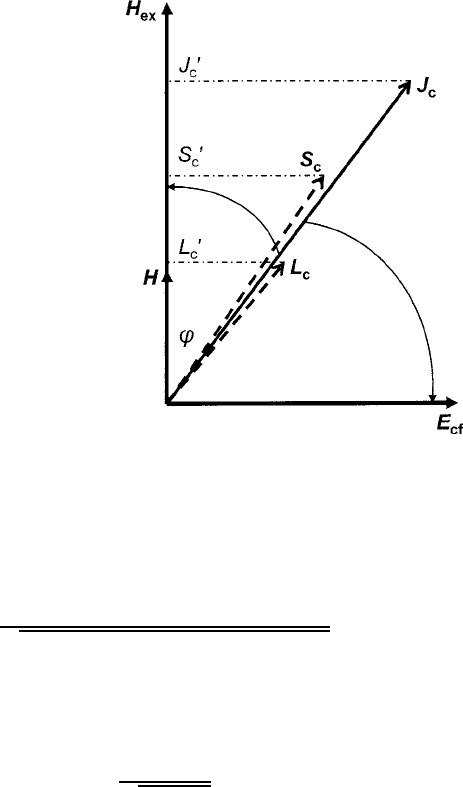
186 4 Ferrimagnetism

Fig. 4.20 The J

effect and

the meaning of the canting

angle 

where the exchange ﬁeld term is from the spin-only version deﬁned in Appendix 4C

and H is an applied ﬁeld that couples both L

and S

, thereby tending to offset the

canting effects of E

on L

.Avalueof then follows from minimization of E./

according to @E . / =@ D 0:

cos  

C J

Œg

C J

H/

C .eE

: (4.37)

For eE

 g

(experiments indicate that both crystal ﬁelds and exchange

ﬁelds produce energy stabilizations of about 10

2

eV), and H

>> H ,(4.37)

reduces to

cos  

C L

: (4.38)

For H

<< H ,cos ! 1 because the applied H ﬁeld overrides the crystal ﬁeld

and realigns L

to S

. For energies 10

2

eV, H would have to approach values

of 10 T.

As a physical rationale for the reduction of J

, this simpliﬁed picture can be

useful. It cannot, however, take into account the crystalline anisotropy of E

that

would manifest itself through a variation of J

with the direction of an applied

magnetic ﬁeld H . Moreover, according to the above model J

should equal J

with

H parallel to E

, a result that has not been observed in measurements with single

crystals. To provide a better interpretation for the actual measurements, we proceed

to examine the crystal ﬁeld inﬂuence in more detail.

4.3 Ferrimagnetic Oxides 187

For a quantum mechanical approximation, angular momentum quenching dis-

cussed in Sect. 2.3.6 can be considered. With the 3d

orbitals, the crystal ﬁeld

Hamiltonian energy dominates spin-orbit coupling or H

>> H

,andL

has

a minor role in magnetic phenomena. With the rare-earth 4f

ions, however,

> H

and L

is fully active magnetically as part of J

, particularly where the

ion is isolated as in paramagnetic systems. When placed in a ferrimagnetic lattice,

however, the J

vector and its L

and S

components are subjected to additional

inﬂuences, according to the perturbation Hamiltonian

D H

C H

D L

 S

C eE

 J

C g

 H C g

 H

D L

C V

C g



C S



H C g

(4.39)

Equation (4.39) mirrors (4.36), except for the V

term that represents a split-

ting of the angular momentum degeneracy instead of a classical precession of the

vector. Here the angular momentum is designated as J

instead of the J

Dionne’s original model because we now consider an actual reduction in J

rather

than simply a trigonometric component. Thus it is appropriate to also redeﬁne to g

such that g

D g

, which represents the magnetic moment component

along the z direction of measurement. Since S

is not inﬂuenced by the crystal ﬁeld,

in reality L

is reduced to L

. We restate that the H

term is expressed in the spin-

only format of Appendix 4C to emphasize that S

is the only relevant momentum

vector (although the b

=U covalent stabilization probably inﬂuences the magnitude

of the J

quenching as part of the crystal ﬁeld effects). Finally, the interaction be-

tween the applied magnetic ﬁeld H and the total magnetic moment now embodied

in the J

D L

C S

vectors is expressed by H

Because of the complexity of the matrix solution involved in carrying out de-

generate perturbation theory with operations that will mix the eigenstates at each

stage of the procedure, no attempt will be made at a formal solution. However, a

qualitative projection can still be made by examining the inﬂuence of the different

perturbation terms.

In a crystalline environment, the rare-earth ion undergoes a lifting of its angular

momentum degeneracy in a manner determined by the analysis of Lea, Leask, and

Wolf [57], from which the ground state terms are listed in Table 4.9.Anexample

of the competing perturbations in a rare-earth ion occupying a cubic oxygen site is

given by the sketches of the energy level structures for the Ho

ion with ground

term

in Fig. 4.21. For this model, we ﬁrst recognize from (4.39) that the largest

term is spin-orbit coupling, typically on the order of 10

1

eV, which splits the J

degeneracy into levels running from

C S

up to

 S

for the group from

to 4f

. The next three terms are smaller by at least an order of magnitude and

each affects a different part of the J

degeneracy. The H

stabilization will lift the

-state degeneracy .J

D 8/ by creating states of lower angular momentum, in this

case a ground triplet T

and various higher energy terms. Despite the small energy

level separations between these crystal ﬁeld splittings (V

 10

2

eV or 100 cm

1

188 4 Ferrimagnetism

Table 4.9 Rare-earth ion ground terms of quenched J angular momentum in O

crystal ﬁelds

Rare-earth ion œL  S term J

DjL

S

Cubic ground term

Mulliken

Cubic ground

term Bethe

3=2

3/2 G



4 A

1 g



9=2

9/2 E

1=2g



3C a

4 A

1 g



5=2

5/2 G



0– –

DjL

C S

7=2

D 7=2 ––

6 T



15=2

15/2 E

5=2g



8 T



15=2

15/2 E

5=2g



6 T



7=2

7/2 E

1=2g



Ground terms taken from the computations of Lea, Leask, and Wolf [57]

Synthetic element

the net result is a signiﬁcantly reduced effective orbital angular momentum J

that carries with it anisotropy consistent with the lattice c-site symmetry. As stated

above, the H

perturbation stabilizes only S

, while H

stabilizes both L

and S

thereby restoring the integrity of L

To account for reduction of L

due to crystal ﬁeld interactions, Van Vleck ﬁrst

reasoned that L

D L

and J

D L

, where the orbital quenching parameter

0    1, and then derived the relation for a modiﬁed g

according to [58]

D  C .2  /



C 1



C S

C 1/  L



C 1





C 1



(4.40)

D  C .2  /

L

C S

After recalculations from the original data, , g

,andJ

entries can be made to

Table 4.8 based on the relation

 D

C 2S

/ cos   2S

C 2S





 2S

: (4.41)

These results reveal a decreasing monotonic trend for J

, J

and a fairly

narrow range of  values .0:3    0:4/ through the upper half of the 4f

series.

From (4.41) an expression for cos can be deduced as

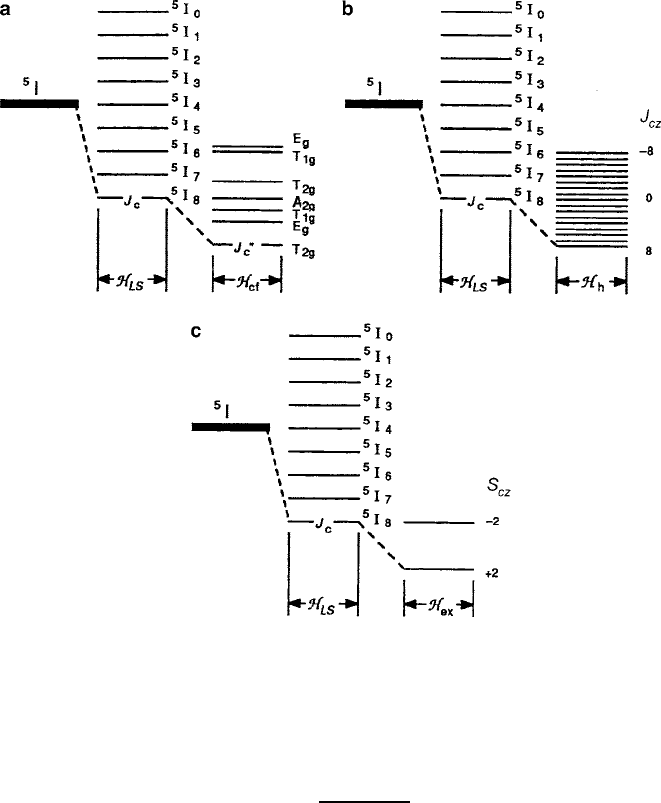
4.3 Ferrimagnetic Oxides 189

Fig. 4.21 Energy-level model of Ho

in iron garnet, isolating the three principal perturbations

that follow the spin-orbit coupling

, i.e., the multiplet structure: (a) the crystal ﬁeld H

;

(b) the Zeeman effect

on the total J

in an magnetic ﬁeld; and (c) the exchange splitting of the

spin only bonding and antibonding states. In this diagram,

is treated as a scalar energy so that

D˙2 for a complete ionic spin ﬂip consistent with the discussion in Sect. 7.1

cos  D

L

C 2S

: (4.42)

If we compare (4.42) with the previous expression derived from (4.38), we note that

both relations point to a increasing  trend with decreasing S

that supports the

experiment-derived values in Table 4.8.

Experiments with Ho

compounds in high magnetic ﬁelds have con-

ﬁrmed that the J

ratio expressed in terms of canting angle  D 51:5

is a

plausible explanation [59]. In applied magnetic ﬁelds exceeding 10 T, J

(or J

)

returned to its uncanted value as the applied H offset the crystal ﬁeld quenching

of L

and restored J

as a good quantum number. In addition to the decoupling

effects on L

 S

, H

introduce anisotropy effects in J

that correspond to the