Dionne G.F. Magnetic Oxides

Подождите немного. Документ загружается.

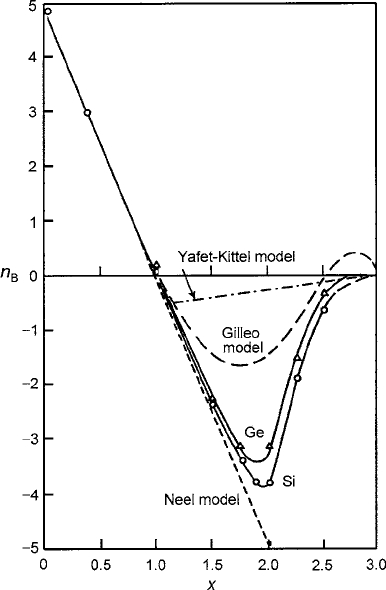
160 4 Ferrimagnetism

Fig. 4.6 Initial canting

effects on magnetic moment

of d -sublattice diluted

yttrium-iron garnet at

T  0 K. Data of

3x

.

3x

where M D Ge

and Si

are from Geller [15]. Figure

reprinted from G.F. Dionne,

J. Appl. Phys. 41, 4874

(1970) with permission.

 1970 by the American

Institute of Physics

spins of the d sublattice experience a weakened a–d exchange ﬁeld, thereby caus-

ing them to react more strongly to their own antiferromagnetic d –d exchange ﬁeld.

This event leads to canting in the d sublattice that causes a lowering of n

.Ifthe

dilution is allowed to continue, n

will reach a peak at some critical value of k

and will eventually drop to zero when the a sublattice is depleted of spins and an

antiferromagnetic ground state takes over in the d sublattice. When the same logic

is applied to dilution of the d sublattice with the more abundant spins, n

will pass

through zero and changes sign when the a sublattice moment becomes dominant.

The net moment then peaks and reverses back towards zero, indicating cancellation

of the a sublattice spins at the point of spin depletion of the d sublattice. These

events are seen in Figs. 4.5 and 4.6.

There have been other diligent attempts to interpret the experimental results of

garnet and spinel spin canting by Borghese [12], Nowik [13], and Rosencwaig [14]

following in general terms the above concepts set down by Gilleo and Geller. A

more comprehensive discussion of spin canting may be found in review articles by

Geller [15] and Gilleo [16]. So far in our discussion, the effects of spin departures

from collinearity have been conﬁned to the state at T D 0 K. More important from

a practical standpoint and also for an understanding of the overall magnetic state of

4.2 Theory of Superexchange Dilution 161

the ferrimagnetic material is the variation of the magnetization or magnetic moment

as a function of temperature, i.e., thermomagnetization over the range 0  T  T

For this analysis, the molecular ﬁeld concepts of the N´eel theory must be revisited.

4.2 Theory of Superexchange Dilution

During the time period of Gilleo and Geller’s work on spin canting, precise calcu-

lated ﬁts to thermomagnetic data were reported by Anderson [17] for yttrium iron

garnet and by Rado and Folen [18] for lithium spinel ferrite. These results pro-

duced accurate values of the molecular ﬁeld coefﬁcients that would serve as the

basis for the magnetic dilution analyses carried out by Dionne [19]. The reﬁnement

to N´eel’s theory emerged from a mathematical representation of Geller’s reasoning

on the effects of selective replacement of magnetic cations by diamagnetic substi-

tutes. Unlike the earlier attempts to develop spin frustration models described in

the previous section that were limited to the interpretation of magnetization as a

function of diamagnetic substitutions observed at T D 0 K, the Dionne theory deals

directly with the inﬂuence of dilution on the molecular ﬁeld stabilization energy that

is the essence of the Brillouin–Weiss thermomagnetization formalism.

4.2.1 Superexchange Energy Stabilization

Since small changes in the exchange energy due to spin canting or frustration will

affect the Curie temperature ﬁrst, the net magnetic moment at T D 0 K will be less

sensitive to the frustration effects of dilution at low levels of diamagnetic substi-

tutions. As a consequence, probabilities of canting can initially be represented by

simple linear approximations. From this approach an analytical formalism for use in

thermomagnetic computations was made possible. Although the correct form of the

effective molecular coefﬁcient relations as functions of dilution was originally de-

duced semiempirically, subsequent theoretical underpinning has been developed to

explain the results. For instructional purposes, we exercise the luxury of discussing

the theoretical basis ﬁrst.

By manipulating (3.27) through and (3.30), we can express the undiluted i and j

sublattice exchange energies in terms of exchange ﬁeld H

, according to

Dm



C H



D2S



C z



; (4.14)

Dm



C H



D2S



C z



;

where S

DS

to observe the proper signs of the opposing i and j sublattices, and

is the number of S

nearest neighbors of spin S

. The removal of a spin, e.g., one

isolated S

, will cause a series of magnetic frustration events in the vicinity of the

missing S

spin as depicted in the sketch of Fig. 4.7.

162 4 Ferrimagnetism

Fig. 4.7 Two-dimensional model of canting of i-site spins surrounding a j -site vacancy

Direct Reduction of Exchange Fields: If a dilution fraction k

exists among the

spins in the j sublattice, the effective number z

and z

are reduced to z



1  k



and z

D z



1  k



. Therefore, the exchange ﬁeld at random i sites,

e.g., S

, produced by the j sublattice will also decrease by the factor



1  k



This ﬁrst-order dilution effect is seen as a direct reduction in the H

component

of (4.14).

Intersublattice Spin Canting: Because the intersublattice S

$ S

interaction

is the dominant antiferromagnetic interaction that establishes the antiparallel spin

alignments between the sublattices, the removalof spins from the j sublattice would

have the indirect effect of causing partial frustration of neighboring spins of the i

sublattice by spin canting. For small dilutant concentrations, we ﬁrst characterize

the canting effect in the i sublattice as the probability k

of a dilutant appearing at

a j site weighted by a canting probability c

, thereby creating a frustration fraction

. To account for the canting of the i-site spin, we then reduce S

by the inverse

probability



1  c



.SinceS

has z

equivalent j sites that can be diluted, the



1  c



factor must be applied z

times to determine the probability of S

making

a full contribution to the exchange energy. The canting reduction factor expressed in

the form of



1  c



can be expanded binomially to



1  z



for small values

of c

4.2 Theory of Superexchange Dilution 163

Intrasublattice Spin Canting: A third frustration effect occurs in the ring of S

nearest neighbors surrounding S

in the i sublattice. The contribution from each

of these S

neighbors that are also neighbors of the missing S

spin would also be

reduced by the



1  c



canting factor because they are crystallographically and

therefore magnetically equivalent in the small dilution limit. If q

of the j sites

in the z

ring shown in Fig. 4.7 are common neighbors to any one of the spins in

the z

ring surrounding S

, their contribution to the H

intrasublattice exchange

ﬁeld term inside the bracket of (4.14) must be reduced by the factor



1  c



which can be expanded binomially to



1  q



for low k

levels. Furthermore,

this canting factor must be applied collectively to all of the spins of the S

ring, i.e.,

times, so that the complete canting factor becomes



1  q



, which is the

probability that none of the S

ring is canted. In the example of Fig. 4.7, z

D 4,

D 2,andz

D 4. Equation (4.14) then becomes

2S



1  z





1  z



C z



1  k





;

2S





1  z



C z



1  k





: (4.15)

Note that the canting factor



1  z



of the i-sublattice spins is also reﬂected in

the intersublattice term of E

If dilution of the i sublattice also occurs, this procedure can be repeated and the

result of these manipulations is the formation of the general relations

2S



1  z



.1  k



1  z





1  k





1  z



;

(4.16)

2S



1  z



.1  k



1  z





1  k





1  z



To a ﬁrst approximation, the parameter c

is treated as a semiempirical constant that

is proportional to the magnitude of the intersublattice exchange ﬁeld coupling to

spin S

relative to the magnitude of the net exchange ﬁeld of the inter and intrasub-

lattice contributions, i.e.,



1  k





1  z



C z



1  k



: (4.17a)

and by symmetry for the opposing sublattice

164 4 Ferrimagnetism

.1  k

/ C z



1  z



: (4.17b)

A test for the validity of the relations of (4.15)and(4.16) can be found from the

corrections to the molecular ﬁeld coefﬁcients required for the ﬁtting of magnetic

moment versus temperature data.

4.2.2 Molecular Field Coefﬁcients

For application to the Brillouin–Weiss theory, (4.16) can be converted back to the

molecular ﬁeld format by ﬁrst deﬁning for the undiluted state

D n

; (4.18a)

D n

;

and

;

I N

;

where n

and n

are the number densities of magnetic ions in the respective

sublattices.

After appropriate substitution for S

, S

and the different J

factors in the brack-

eted exchange ﬁelds, (4.16) can now be expressed as

g



C N



; (4.19)

g



C N



;

where

D M

.1  k

/ (4.20)

D M



1  k



4.2 Theory of Superexchange Dilution 165

and

 N



1 



1 C





;

 N



1 



1 C





;

D N

 N



1  z



1  z



; (4.21)

 N



1  z

 z



In this conversion to molecular ﬁeld format, it should be noted that the dilution

factors .1  k

/ and



1  k



have been absorbed into M

and M

, thereby reﬂecting

the appropriate reduction in sublattice magnetizations. For convenience as much

as any other reason, the canting or frustration factors have been included in the

deﬁnitions of the molecular ﬁeld coefﬁcients for computational convenience with

the Brillouin–Weiss function, as will be demonstrated for the case of the magnetic

garnet system.

4.2.3 Solution for Yttrium Iron Garnet

For d and a sublattices of the garnet system (e.g., Y

), the relevant parame-

ters are as follows: z

D 4, z

D 6, z

D 4, z

D 6; q

D q

D 2.Ifthese

values are applied in (4.21) the molecular ﬁeld coefﬁcients become

 N

.1  12c

 N

.1  18c

/; (4.22)

 N

.1  4c

 6c

In Dionne’s original work [19], the above molecular ﬁeld relations were applied to

the yttrium iron garnet (YIG) system. For the convenience of relating the results to

chemical formulae, the sublattice magnetic moments were expressed per formula

unit or molecule .M/ rather than per unit volume (M for magnetization). In the

text that follows, wherever the discussion involves this particular model,

.T / D M

.0/ B

/; (4.23)

.T / D M

.0/ B

where

.0/ D 3g

.1  k

/.1 0:1k

and

.0/ D 2g

.1  k



1  k

5:4



; (4.24)

166 4 Ferrimagnetism

where Avogadro’s number N

is required to convert per molecule to per mole. The

additional factors are small adjustments that were created empirically to provide a

close ﬁt to experiment and bear no relation to the present frustration model or those

discussed in the previous section. The corresponding parameters a

and a

are

.T / D

.d /

ŒN

C N

; (4.25)

.T / D

.a/

ŒN

C N

:

Because the exchange ﬁelds (inside brackets) are in units of oersteds, the N

co-

efﬁcients will be dimensionless if M is expressed in gauss (or emu=cm

). As a

consequence, the conversion factor between M



emu=cm



and M (emu/mol) must

be absorbed in the N

coefﬁcients that are now expressed in units of mol=cm

.For

these purposes, the units of H

.i/

is that of the factor multiplying the magnetic mo-

ment m

D g

, i.e.,

.i/

; (4.26)

in emu=cm

By ﬁtting theory to data compiled from magnetic moment measurements as a

function of temperature, the following relations for the molecular ﬁeld coefﬁcients

were deduced as functions of dilution:

30:4 .1  0:87k

/ 30:4



1 



;

65:0 .1  1:26k

/ 65:0



1 



; (4.27)

D N

C97:0 .1  0:25k

 0:38k

/ C97:0



1 





for dilution limits k

 0:65 and k

 0:35.

Comparison of theory with ex-

perimental data of Geller et al. [20] is shown in Fig. 4.8 for the

ŒFe

2x



.Fe

3x

/ O

system that includes both d and a sublattice dilution. To convert

among the N

’s, N

’s and J

’s, the following relation based on (3.28) between their

magnitudes can be used.





; (4.28)

Note that the sign of N

is designated as positive. This serves to account for the sign reversal in

the sublattice moments. An alternative convention would be to leave all of the coefﬁcients negative

and change the sign in the expression for the exchange ﬁeld to indicate the opposing contributions

of the antiferromagnetically aligned spins.

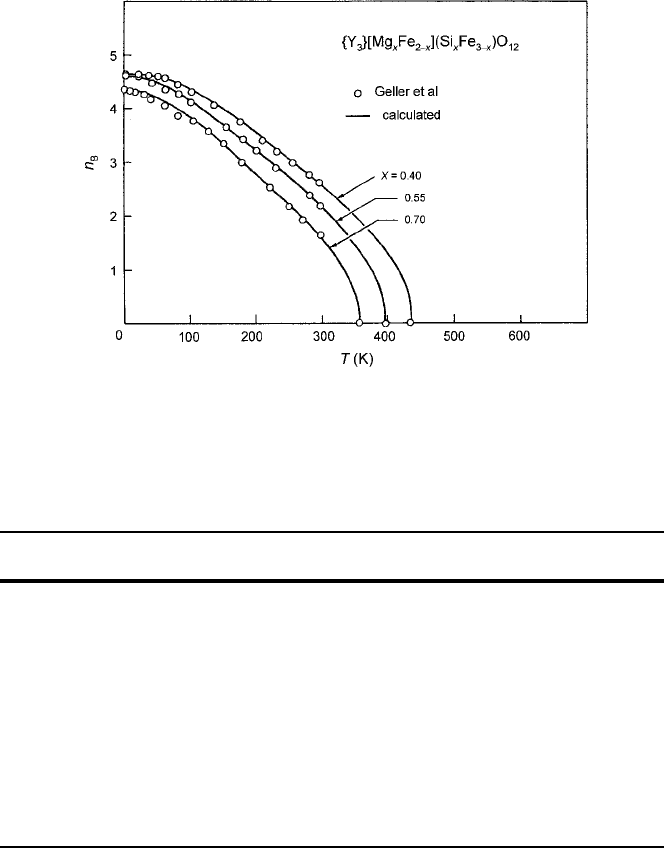
4.2 Theory of Superexchange Dilution 167

Fig. 4.8 Comparison of theory with experiment for three compositions of fY



2x



3x

, which feature substitutions in both sublattices. Figure reprinted

from G.F. Dionne, J. Appl. Phys. 41, 4874 (1970) with permission.

 1970 by the American

Institute of Physics

Table 4.1 Molecular and exchange ﬁeld parameters of yttrium iron garnet and lithium spinel

ferrite calculated from theory

emu=

mol=N

ergs H

(T)

W n

mol 10



4

15



T D 0 K

(

4 W 3

4 W 2

(

8:4

5:6

(

30:4

97:0

(

347

1107

(

2:4

4:9

288

(

8 W 2

6 W 3

(

5:6

8:4

(

65:0

97:0

(

742

1107

(

1:6

4:9

451

0:5

2:5

(



4:5

W 1:5

6 W 1

(

4:2

2:8

(

60

273

(

212

969

(

2:1

4:8

510

(



4 W 1

W 1:5

(

2:8

4:2

(

150

273

(

533

969

(

3:8

4:8

720

In the determination of these parameter values, the lattice parameter of the garnet a

 12:4

and of the spinel a

 8:4

By convention, all J

values are negative

These values reﬂect the 25% initial dilution of the B sublattice by Li

ions

where a

is the lattice cubic cell dimension (containing eight molecules for garnets

and spinels) and g

D g

D 2 for the 3d

group. In Table 4.1, where a summary

of these parameter values is given, the sign convention mentioned above for the N

and N

has been adopted. Note that the values of H

.i/

computed from (4.26)for

each sublattice of the garnets and spinels is in the range of 10

–10

168 4 Ferrimagnetism

As predicted by (4.22), the relations of (4.27) are linear and the coefﬁcients of k

and k

are in the approximate 3:1 ratio as they appear in the intra and intersublattice

factors. Moreover, the values of the frustration parameters c

and c

computed from

these results are 0.070 and 0.0725, respectively, or about 7% for both sublattices.

By means of the values from Table 4.1 applied to (4.15) with S

D S

D 5=2 for

ions, computations show that the ratio of c

and c

are approximately equal,

conﬁrming the equality of this low dilution limit frustration factor between the two

sublattices.

Other attempts to model the thermomagnetic properties of the iron garnets based

on this seminal work produced reﬁnements for speciﬁc ionic dilutants. Notewor-

thy among these efforts was the work of R¨oschmann and Hansen in support of

research into the magneto-optical properties of the diluted garnets to be discussed

in Chap. 7 [21].

In addition to the YIG-based system and the rare-earth iron garnet system [3, 4,

22] to be examined in Sect. 4.3.3, Dionne also analyzed the lithium spinel ferrite

family [5,23] and later included high-permeability nickel-zinc and manganese-zinc

spinels commonly used for inductor cores and in magnetic recording applications

[24]. Although the superexchange interactions are more complicated than in the

simple garnet system because of the presence of multiple species of cations such as





and Mn





, the principles of magnetic dilution apply in the same

manner. Details of the diluted spinel system lithium-zinc-titanium ferrite that is par-

ticularly important for microwave applications are summarized in Appendix 4A.

In the present analysis, higher order canting effects within the diluted sublattice

have been ignored at low dilution levels. Part of these effects appear as second-

order terms in k

and k

that enter through the z

D z



1  k



dependencies

in (4.16).

The dilution theory developed from elementary probability arguments conﬁrms

the original experimental ﬁndings for yttrium-iron garnet (YIG). The earlier work

led to the conclusions that (1) the dilution relations are at least initially linear for

each of the molecular-ﬁeld coefﬁcients, (2) the dilution of one sublattice does not

inﬂuence its own intrasublattice coefﬁcient (N

or N

) to ﬁrst order, and (3) the

reduction of the intrasublattice coefﬁcient is three to four times greater than that

of the intersublattice coefﬁcient (N

or N

). Note that the reduction in exchange

energy E

is not directly caused by the J

exchange constants, which are ﬁxed by

covalent bonding between individual magnetic ion pairs. The effect is manifested in

the molecular-ﬁeld coefﬁcients because it is the dilution of z

spin neighbors (see

(4.21)) that causes exchange frustration between the opposing sublattices, generally

referred to as spin canting.

4.3 Ferrimagnetic Oxides

In the previous section, some of the basic concepts peculiar to ferrimagnetism were

described. In particular, the behavior of the spontaneous magnetism and its rela-

tion to the magnetic exchange was explained. The actual magnetic properties of the

4.3 Ferrimagnetic Oxides 169

various ferrimagnetic systems are important in themselves, however. Although they

have been documented in other volumes, failure to include at least the basic prop-

erties of standard ferrite compounds in this text would be a conspicuous omission.

The following subsections will attempt to deﬁne the spinel, garnet, and hexagonal

ferrites of general interest to workers in the ﬁelds of magnetics. Some of the more

unusual or anomalous issues will be treated as the subjects arise in later parts of

the book.

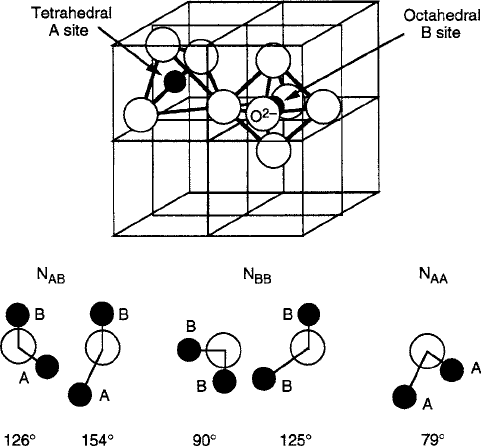
4.3.1 Spinel Ferrites A



The 2:1 octahedral B to tetrahedral A site ratio in the spinels lattice is determined

by the crystal lattice structure sketched in Fig. 4.9. Unlike the garnets that will be

discussed next, this cell features congruity between the overall crystal axes to those

of the individual sites. In its generic form the spinel can be (1) normal, with the di-

valent ions occupying only B sites, i.e., A





, or (2) inverse, in which

the divalent ion resides in A sites. In most practical cases, the ferrite is a mixture

between normal and inverse. A number of excellent references document the prop-

erties of spinel ferrites: Smit and Wijn [25], von Aulock [26], Gorter [7], Blasse

[27], von Grenou [28], Folen [29], Griefer [30], and Schieber [31]. The magnetiza-

tion properties of common spinel families are described in the following paragraphs

Fig. 4.9 Spinel crystal structure with bond angle diagrams