Dionne G.F. Magnetic Oxides

Подождите немного. Документ загружается.

5.1 Quantum Paramagnetism of Single Ions 211

Table 5.2 3d

transition group data

Free ion Ti





1



154 104 87 85 – –100 –180 –335 –852

55 57

Hund term

3=2

5=2

9=2

3=2

High spin – – –





























































Lowspin– –––––

















































S(hs) 1/2 1 3/2 2 5/2 2 3/2 1 1/2

(ls) 1 1/2 0 1/2 0

hgi 0to1:9 1:9 1.9–2 1.9–2 2>37>4 >2:252–2.5

Data obtained from W. Low, “Paramagnetic Resonance in Solids,” (Academic Press,NewYork

1960) Table XIX [13]

Low-spin states can occur in lower symmetry crystal ﬁelds that split the E

degeneracy sufﬁ-

ciently to cause a violation of Hund’s rule by creating a spin pair in the lower e

state

are only a small fraction of those in the iron group with the result that free-ion states

can now include the L  S interaction and the perturbation calculation employs

J as the quantum operator and begins with the spin–orbit multiplet functions. The

shielding of the 4f electrons by the ﬁlled 5s and 5p shells is contrasted with the ex-

posed 3d shell in the iron group by comparison of the calculated radial distributions

[11] shown in Fig. 5.4. As a consequence, the S operator alone does not enter the

picture until exchange effects are present as discussed in Sect. 4.3. The Hamiltonian

operator of concern for the single-ion analysis of rare-earths is therefore that of

the point-charge crystal ﬁeld model of Stevens [12] and Hutchings [13], which is

expressed in general terms of operator equivalents as

l;m

; (5.15)

where the coefﬁcients B

are related physically to the atomic number of the

cation, its ionic radius, and the interionic distances. There is additional mathemat-

ical formalism that relates B

to another set of coefﬁcients designated as A

multiplied by constants ˛

, ˇ

,and

for respective values of l D 2,4,and6,which

may be computed but are usually determined semiempirically for the particular sit-

uation. A partial list of operator equivalents is given in Table 5.3 forsomeofthe

more signiﬁcant crystal ﬁeld components. More comprehensive lists are found in

the papers by Stevens and Hutchings cited above, as well as the book by Low [14].

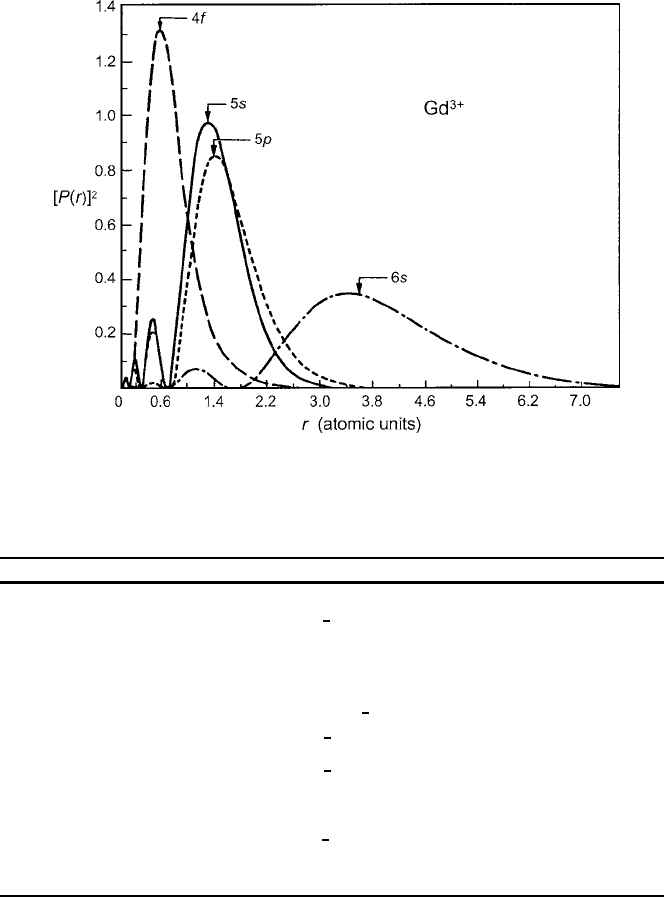
212 5 Anisotropy and Magnetoelastic Properties

Fig. 5.4 Radial densities of Gd

Hartree–Fock wavefunctions. Figure reprinted from [11]

with permission.

 1962 by the American Physical Society. http://link.aps.org/doi/10.1103/

PhysRev.127.2058

Table 5.3 Partial list of lower-order crystal ﬁeld operator equivalents

Electrostatic potential Operator equivalent Notation



 r



˛

 J

J C 1





y



 J





35z

 30r

C3r



35J

 30J

J C 1

C25J

 6J

J C1

C3J

J C 1



 r



y



.BH /

max

4M



3xy











6x





.231z

315z

C105z

5r

/

231J

 315J

J C 1

735J

C105J

J C 1

525J

J C 1

C294J



J C 1

C40J

J C 1

60J

J C 1



Based on theory developed by Stevens [11]

5.2 Anisotropy of Single Ions

The foregoing discussion included the case of a single d electron occupying a sin-

glet ground state stabilized from the T

triplet term by an axial tetragonal ﬁeld or

possible Jahn–Teller distortion of an octahedral site. This situation represents a type

5.2 Anisotropy of Single Ions 213

of building block for the remainder of the d

series, and we shall now review the

essential features of each member, ﬁrst with regard to the g factors and the inﬂuence

of partially quenched orbital angular momentum on anisotropy, and then in relation

to magnetostriction. Although most of the discussion will focus on octahedral lig-

and coordinations, the contributions from tetrahedral sites will be pointed out where

appropriate.

5.2.1 3d

and 3d

D-State Triplet

In the previous section, the example of the d

orbital singlet ground state was

analyzed to illustrate theoretical tools available for determining the single-ion para-

magnetic anisotropy. In most situations, the electronic structure is not so amenable

to analysis because the orbital ground state is not a singlet or involves an even-

integer spin state (S D 1 or 2) that does not produce Kramers doublets, which are

spin degeneracies that cannot be removed by a crystalline ﬁeld and occur in odd

numbered d-electron systems [15]. Furthermore, when the spin–orbit coupling op-

erator is introduced to the calculation, energy multiplicities increase to the extent

that the one-electron approximation must give way to the complete analysis in order

to gain a more accurate picture of the electronic structure. However, unless detailed

spectroscopy issues arise, we shall work with the simpler models.

To continue the discussion of the previous section, we ﬁrst consider the case

where the threefold orbital degeneracy of the lower T

state of the free-ion D term

is not fully quenched. This occurs with Ti





and Fe





as described by the

one-electron ground state diagrams and the corresponding multiple electron energy

level structure of Fig. 5.5.Forthed

case, it is convenient to view the degeneracy as

arising from the single electron that begins the second half of the d shell, recalling

that the ﬁrst ﬁve are locked into collinear spin polarization dictated by Hund’s rule

with L D 0 that therefore contribute nothing to the orbital degeneracy. [A similar

approach can be made for the case of two electrons in the T

states (d

or d

)by

treating the source of degeneracy as spin vacancies or “holes” in the T

shell]. For

both d

and d

ions, the triplet can be further stabilized as a singlet (analyzed in

the previous section) or as a doublet, which can have an important inﬂuence on all

magnetoelastic properties because the remaining degeneracy carries orbital angular

momentum into the ground state, and hence a strong spin–orbit link to the crystal

lattice.

Despite the success in interpreting the data for the orthorhombic crystal ﬁeld of

as an impurity substituted for Al

in certain hydrated alum salts [generic

formula .R  6H

.Al  6H

.SO

2

,whereR

is a large monovalent

(alkali metal) ion] described above, there remains uncertainty about the origins of

the lower symmetry crystal ﬁeld across the various members of the alkali metal

members of this family. An examination of the data in Table 5.1 reveals a curious

correlation between the strengths of lower symmetry crystal ﬁelds and the radius

of the monovalent ions. The smaller the radius, the smaller the lattice parameter

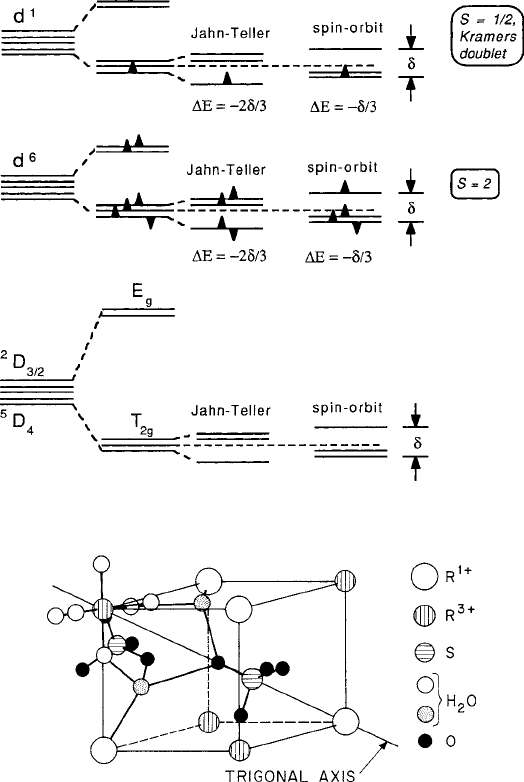
214 5 Anisotropy and Magnetoelastic Properties

Fig. 5.5 Electronic structure of d

and d

conﬁgurations: one-electron and combined electron

models

Fig. 5.6 Structure details of one octant of an ’-type alum lattice, with trigonal symmetry axis

indicated. Figure reprinted from [6] with permission.

 1968 by the American Physical Society.

http://link.aps.org/doi/10.1103/PhysRev.172.325

(Vegard’s law), and the greater is the departure from cubic symmetry. This recogni-

tion led to the local crystallographic model [6] that began with an axial ﬁeld along a

111

axis of each .Ti  6H

complex that is inﬂuenced by a trigonal distortion

of a tetrahedral grouping of sulfate radicals .SO

2

illustrated in Fig. 5.6.Since

the monotonic reductions in lattice parameter from Cs, Rb, Tl, K, through to Na

correlate with increases in the T

splittings, it is reasonable to presume that the

trigonal ﬁeld would increase accordingly, preserving the condition ı>

that is

necessary to stabilize the orbital singlet in the T

shell, as discussed in Sect. 2.4.

5.2 Anisotropy of Single Ions 215

The appearance of a further distortion as the smaller alkali ions were introduced

was attributed to local lattice adjustments needed to accommodate the larger Ti

ion (0.76

A radius) into the smaller host Al

(0.51

A) site. Another mechanism

would stabilize the d

singlet by a Jahn–Teller effect that causes a tetragonal z-

axis expansion of the H

O octahedron that is set up along the

100

cubic lattice

axes. The combined distortions then account for the lower than axial symmetry that

gives rise to the expected twelve equivalent paramagnetic complexes reported for

RbAlTi alum [3,4].

Another concern is the concentration-dependent factor of spin–orbit stabilization

that can occur in magnetically ordered situations induced by local exchange ﬁelds

due to clustered Ti

impurity sites. A perturbation analysis of the T

splitting from

100

axial distortion, spin–orbit coupling, and an exchange ﬁeld is presented for

the d

case in Appendix 5B. From this model, it is concluded that (2.34)forthe

threshold condition of doublet stabilization should be modiﬁed according to [16]







1 C



; (5.16)

for ı<gm

. This approximation loses validity when H

decreases with tem-

perature as described by a Brillouin function, reaching zero at the Curie or N´eel

temperature. Based on the results from Ti

in Rb alum with 

D 154 cm

1

and

ı 10

1

deduced from the anisotropy of the measured g factors, this effect will

produce S–O stabilization only if ı is signiﬁcantly less than 

regardless of the

value of H

. Moreover, the observation of paramagnetic resonance (EPR) signals

from regions dominated by antiferromagnetic ordering is questionable. Nonetheless,

any unquenched orbital momentum in a ground-state doublet could increase mag-

netoelastic effects that would enhance EPR line broadening through spin–lattice

relaxation, as discussed in Chap. 6.

The earliest work on undiluted CsTi alum by Bleaney et al. [7] reported reso-

nances with trigonal ﬁeld Zeeman splitting factors g

łł

D 1:25 and g

D 1:14 and

very large homogeneous linewidths even at the lowest temperature of 1.2 K. Such a

result gave credence to the argument that strong spin–orbit–lattice interactions could

be rendering ı<

and allowing the line broadening to take place from a rapid

Orbach relaxation process (see Chap. 6). A small axial strain that allows an orbital

doublet ground state could be the result of a trigonal axis contraction from a J–T

effect in the T

term, encouraged further by interionic Ti

exchange at T  4K.

Subsequent experiments by Woonton and MacKinnon [8] with dilute specimens of

CsTiAl alum tended to conﬁrm the Bleaney results. These later results, however, in-

dicated that a smaller splitting



10

1



of the T

state likely exists and could

explain a stronger than usual inﬂuence of the l

D˙1 doublet. Later, work reported

by Dubicki et al. [17] and Pigott et al. [18] have also suggested that spontaneous

orbit–lattice deformation within the T

manifold could contribute to the observed

peculiarities in the CsTi case.

Another occurrence of the Ti

octahedral water complex worthy of mention

is as a dopant in sapphire Al

. In low concentrations this cation creates the

216 5 Anisotropy and Magnetoelastic Properties

blue-colored gem, but its technical importance lies in the 5,000

A wavelength, i.e.,

10Dq  2:5 eV , of its optical transition which is useful for laser applications. The

crystal ﬁeld is trigonal, with a ligand coordination depicted in Fig. 2.6. Magnetically,

the g-factors g

łł

D 1:067 and g

<0:1reported by [19] as S–O stabilized doublet

ground state modiﬁed by dynamic Jahn–Teller effects, which suggests a ﬁeld oppo-

site in sign to that of CsTi alum. This interpretation was proposed by Ham [20]and

later analyzed by Macfarlane et al. [21], Bates and Bentley [22], Stevens [23]and

Abou-Ghantous et al. [24]. The question of how the degeneracy of the T

state is

lifted can be viewed in the context of Jahn–Teller (singlet) vs. spin–orbit (doublet)

stabilizations introduced in Sect. 2.4. In either case an axial (or lower) symmetry

crystal ﬁeld must occur by distorting of the ligands, if an appropriate lower sym-

metry ﬁeld is not already present. Even if there is a lower symmetry component, a

spontaneous distortion to enhance (or reduce) the existing ﬁeld is always a possibil-

ity, as appears to occur in ferrimagnetic spinels and garnets.

The principal 3d

ions of interest are Fe

and Co

, usually occupying an

octahedral site.

Despite the similarities of the ground state, this conﬁguration dif-

fers from the 3d

case in various ways. With an even number of spins, there are

no Kramers doublets to enable microwave spectroscopy; the value of Dq can be

smaller if the cation valence charge is lower; the sign of the multielectron spin–orbit

coupling constant 

is negative because the contributing L and S vectors of all

ions with n>5(upper half of the shell) are in opposite directions. This latter

condition causes the g factor to increase to values greater than 2 in the perturbation

analysis result given in (5.8)and(5.12), therefore causing an increased magnetic

moment and greater paramagnetic anisotropy. Despite the absence of Kramers dou-

blets in this even-electron system, microwave resonance measurements were carried

out on Fe

in MgO because the negative 

combined with small-to-moderate ı

splittings of the T

term likely caused by local random J–T effects that produced

isotropic g D 3:47 and 6.83 [25].

An even more important effect for magnetoelastic properties is the occurrence

of low and intermediate spin states with the higher valence Co

ion because the

shell is occupied. As pointed out in Sect. 2.4 (Fig. 2.19b), because of the intra

exchange energy U

that compels the alignment of spins, the occupation can assume

various conﬁgurations, depending on the relative values of 10Dq and U

.InFig.5.7,

various situations are depicted. For the high-spin (hs) case of S D 2 with U



10Dq,theE

shell is half-ﬁlled, and all of the magnetoelastic effects are the result

of T

occupancies. Similar J–T stabilizations of an orbital singlet will occur for

either a trigonal or tetragonal ligand distortion. However, inspection of the orbital

lobes in relation to the ligand charges indicates that the local-site magnetostriction

will be 

111

>0in the trigonal case (which has been conﬁrmed with Fe

)and



100

<0from a tetragonal contraction, typical of Co

. As a consequence, the

singlet is stabilized with energy deﬁned as E D .2=3/ı

in either case. At the

extreme where U

 10Dq, all six spins condense into a low-spin (ls) S D 0 state

See footnote at end of Sect. 2.4 for comment on Fe

in a tetrahedral site.

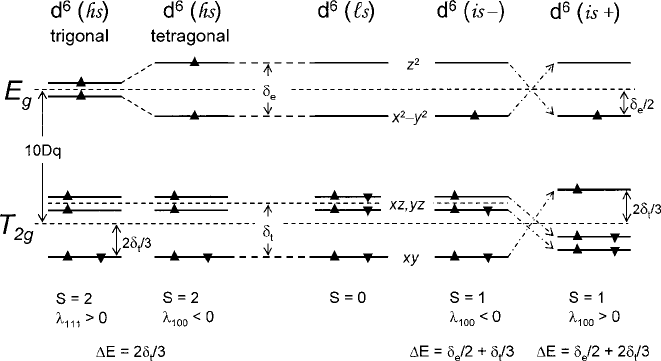
5.2 Anisotropy of Single Ions 217

Fig. 5.7 Aufbau diagram of various octahedral-site distortions induced by S–O or J–T stabiliza-

tions of d

spin conﬁgurations. Symbols hs, ls, ˙is indicate high, low, and intermediate spin states

to fully occupy the T

shell, thereby creating a diamagnet. The most interesting

situation arises where U

 10Dq, allowing the formation of intermediate-spin

states (is-) and (is+) that are diagrammed in Fig. 5.7. In these two cases both the

and T

shells are occupied, such that the conventional J–T splitting of the e

states provides a strong stabilization ı

/2 that is augmented by either .1=3/ı

.2=3/ı

, depending on the sign of the axial distortion. The implications of these

competing possibilities become evident in experiments where the magnetostrictive

strains reverse from 

100

<0to 

100

>0[31] of Chap. 2.

Most signiﬁcant are the properties associated with magnetic exchange. Because

of the partially ﬁlled e

states that allows for strong exchange coupling, S–O sta-

bilization of the T

term can occur in ferro- or ferrimagnetic systems such as

magnetite Fe

, enhancing anisotropy and magnetostriction effects discussed in

Sect. 5.3. In tetrahedral sites, d

and d

become pure Jahn–Teller ions with the

lower E

doublet term split to stabilize a singlet ground state. An example is Fe

in the uncommon spinel Fe





[26].

5.2.2 3d

and 3d

D-State Doublet (J–T Effect)

For the classic Jahn–Teller conﬁgurations, the g factors are not strongly inﬂuenced

by the ligand environment for the simple reason that the ground state E

doublet

described by the diagrams in Fig. 5.8 contains no orbital angular momentum. The

inﬂuence of the upper

and

states therefore occurs through mixing by the

L  S operator, but as the perturbation theory dictates, the effect on g

will be re-

duced to terms on the order of LS =10Dq  10

2

in most situations – signiﬁcant

218 5 Anisotropy and Magnetoelastic Properties

Fig. 5.8 Electronic structure of d

and d

conﬁgurations: one-electron and combined electron

models

but not substantial for spin–lattice interaction considerations. Moreover, the d

con-

ﬁguration does not yield Kramers doublets for convenient microwave spin resonance

analysis of the g factors. A multielectron calculation of the electronic structure is

described by Low [27] that reveals the expected ﬁve-fold ladder of levels split ac-

cording to 

= multiples. Regrettably, the effect of a strong Jahn–Teller splitting

of the E

doublet was not found in the literature. The most common example of

this conﬁguration is Mn

(although Fe

makes an occasional appearance in non-

stoichiometric garnets and other magnetic oxides). It almost universally occupies

octahedral sites in oxygen coordinations

and therefore brings with it structural per-

turbations associated with the attendant J–T tetragonal distortions of the ligands

that manifest themselves as magnetostriction effects or actual crystallographic phase

changes when they become cooperative. In mixed-valence situations with Mn

, charge transfer mechanism can provide interesting and sometimes anoma-

lous electrical conductivity behavior, as will be examined in Chap. 8.

There is evidence that Mn

(and Cu

) in ferrites enters tetrahedral sites in ferrimagnetic oxides

where it can stabilize a doublet ground state in the T

shell with unquenched orbital momentum

through spin–orbit coupling. The implications of this possibility are examined in relation to mag-

netostriction and spin–lattice relaxation in Sect. 5.3.6.

5.2 Anisotropy of Single Ions 219

The paramagnetism of d

is seen most commonly in Cu

whichservedasthe

vehicle for the discovery of the J–T effect discussed in Sect. 2.4.3, and in that respect

parallels the magnetoelastic behavior of the d

conﬁguration. In early EPR work

with the cupric salts, g-factors in the range of 2–2.5 were found, consistent with the

expectation for <0[27] and theoretical discussions have been reported by Pryce

[28] and Bates and Chandler [29]. The importance of this ion, however, may reside

more in its charge transfer capability with Cu

and Cu

oxidation states for high-

temperature superconductivity (also discussed in Chap. 8 than in its fundamental

magnetism. The low spin value contributes little to magnetic systems and although,

like Mn

, its magnetoelastic capability can assist in tailoring magnetostriction in

magnetic oxides, cooperative J–T effects on lattice structural phases can sometimes

be more of an irritant than an asset.

5.2.3 3d

and 3d

F-State Triplet

In octahedral sites, the two d-electron case produces a ground-state triplet similar to

that of the d

and d

cases, and can be treated in a similar manner by considering

the T

state as occupied by a single spin vacancy or hole for simple approxima-

tions. However, an important distinction must be made. The total L value for these

conﬁgurations is 3 instead of 2 (Fig.2.3). This means that the free-ion term is F ,

not D, and there are seven orbital states instead of only ﬁve. The distinction be-

comes particularly of interest for optical transitions because of the different orbital

splitting energies. For F states, the ﬁrst expected orbital term above a ground triplet

is the other triplet which is separated by 8Dq. Nonetheless, the ground state can

still be treated by the single electron model for our present purposes. Inspection of

the diagrams of Fig. 5.9 indicate that J–T and S–O stabilizations can take place in

a manner similar to the d

and d

cases, but with inverted electronic energy struc-

tures. This feature will be examined more critically in relation to magnetostriction

and spin–lattice relaxation in ordered spin systems. The splitting of the lower triplet,

however, will contribute signiﬁcantly to the single-ion anisotropic g factors because

the ı splittings are small enough to render denominator of the 

factor in the spin

Hamiltonian in (5.11) small enough to cause a signiﬁcant departure of the g-factor

from the isotropic spin-only value of 2. For this reason, g factors for V





and Co





in MgO have been measured, respectively, as 1.92 [30] with

a positive  D 104 cm

1

and 4.28 [31] with a negative  D180 cm

1

When the d

case is analyzed in the multielectron

F term format, the degenerate

state is lowest and its threefold degeneracy can be approximated by a pure P

state with L D 1 [32, 33]. This approach simpliﬁes the perturbation calculation

by the adoption of an effective spin–orbit coupling operator to produce a set of

orbital states with Kramers spin degeneracies included. For our purposes, however,

the one-electron model is sufﬁcient to gain a physical understanding of how spin–

orbit coupling can further stabilize an unquenched orbital doublet by enhancing the

effects of an exchange ﬁeld. This effect can account for the large Co

anisotropy

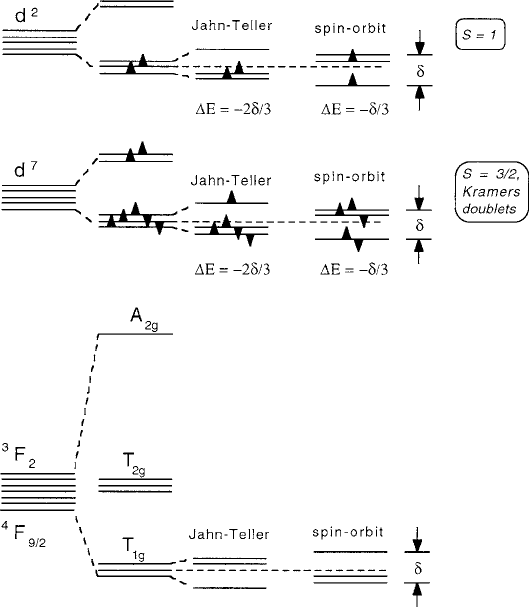
220 5 Anisotropy and Magnetoelastic Properties

Fig. 5.9 Electronic structure of d

and d

conﬁgurations: one-electron and combined electron

models

contributions in magnetically ordered systems. It can also help to explain the source

of the small orbital contribution to the paramagnetic anisotropy and magneto-optical

effects of the S-state Fe

ion in cubic crystal ﬁelds typical of spinel and garnet

ferrimagnets.

5.2.4 3d

and 3d

F-State Singlet

The inﬂuence of orbital angular momentum on the paramagnetism and anisotropy

of the g factors is felt less in the F state cases, where the A

singlet in cubic

ﬁeld is lowest, as shown in Fig. 5.10 for d

and d

conﬁgurations in an octahedral

site. With the ﬁrst excited orbital state separated in energy from the ground state

by 10Dq, a smaller 8=10Dq correction to g in (5.12) can usually be expected.

The most studied ion of this type in an octahedral site is Cr





, with a spin