Dionne G.F. Magnetic Oxides

Подождите немного. Документ загружается.

5.3 Magnetocrystalline Anisotropy and Magnetostriction 241

bipyramid sites with large axial symmetry components greatly inﬂuence the overall

anisotropy once the iron spins are ordered by magnetic exchange. In terms of (5.18),

one could conclude that the " parameter increases and produces a greater mixing of

the relevant excited orbital term with the ground

5=2

term. More interesting cases,

however, are those that involve lower symmetries and cations with strong intrinsic

anisotropies that arise from unquenched orbital angular momentum.

5.3.5 Cooperative Single-Ion Effects: Anisotropy

Although Fe

ions collectively dominate the magnetic moments of many ox-

ides, the major contributions to magnetic anisotropy and magnetostriction are often

provided by small concentrations of ions that have unquenched orbital angular

momentum. Interactions between the magnetic moments and the lattice can be sig-

niﬁcant in both the iron group and rare-earth ions. In the rare-earth 4f

series

spin–orbit coupling is strong for all of the members (except Gd

because of its

L D 0 ground state), but crystal ﬁeld effects are small. Nonetheless, the spin–orbit–

lattice interactions are large enough to produce very short spin–lattice relaxation

times in the microwave band (discussed in Chap. 6), and can create giant magnetoe-

lastic effects in certain noncubic intermetallic compounds such as NdFeB alloys for

permanent magnets and Tb

1x

(terfenol-D) for magnetostrictive transduc-

ers. In oxides, however, the large magnetoelastic effects of rare-earth ions can be

equaled by selected ions of the 3d

series that are stabilized in an exchange ﬁeld by

spontaneous local lattice distortions.

Recalling the discussions in Sect. 2.4, we ﬁrst recognize the orbital angular

momentum as the key to the coupling between the spin and lattice systems. Spin–

orbit stabilization of the l

D˙1 doublet, therefore, would be a prerequisite for

anisotropy and spin–lattice relaxation rate





–



, with the attendant lattice distor-

tion contributing to magnetostrictive extension or compression, depending on the

sign of the stabilization. Local Jahn–Teller stabilizations of the l

D 0 singlet would

be expected to contribute to magnetostriction once they become cooperative, with

anisotropy and relaxation effects appearing as lower order phenomena. In Table 5.9,

the expected results are compiled for the various iron-group ions in octahedral and

tetrahedral situations, based on the discussions in Chap. 2. Although each member

of the series has the potential to cause local perturbations, only ﬁve (d

through d

)

have consistently demonstrated exchange coupling strong enough to inﬂuence coop-

erative magnetoelastic effects in magnetically ordered compounds. In the following

text, reference will be made to this summary in the context of speciﬁc ions.

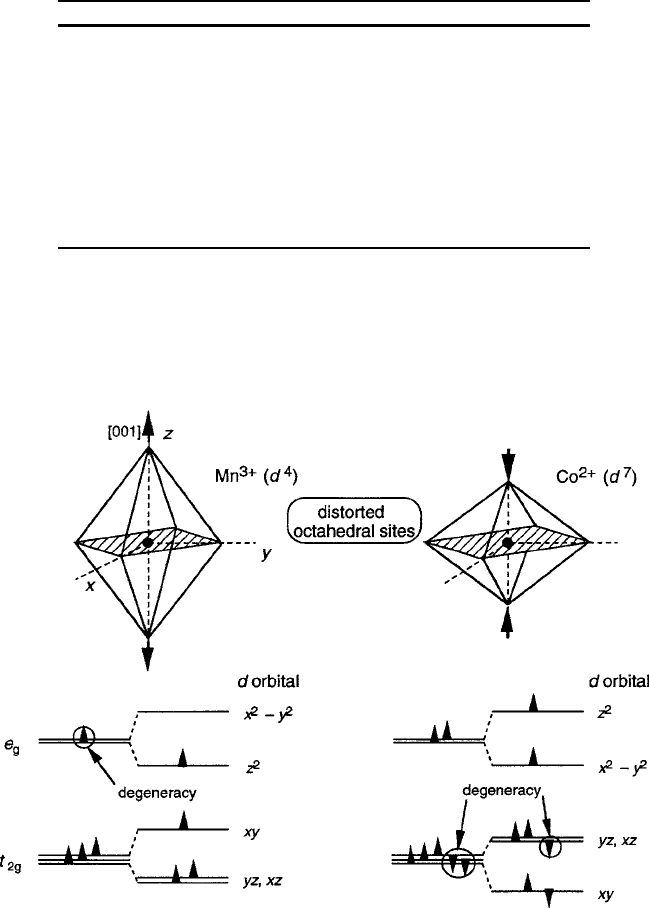
For the discussion of anisotropy, we begin with the case of the T

triplet term,

which is contrasted with the E

case in Fig. 5.20 using the one-electron examples of

and Mn

in an octahedral site. Here the ground state from the crystal-ﬁeld

distortion can be either a singlet or doublet, depending on the sign of the splitting

parameter ı. To understand these effects, consider the case of Co

, now compared

with Fe





in Fig. 5.21. Both present a T

triplet in an octahedral ﬁeld and

242 5 Anisotropy and Magnetoelastic Properties

Table 5.9 Single-ion anisotropy and magnetostriction contributions of

high-spin 3d

ions as substitutions in Fe

ferrite sites

N Ion K



100



111

H

Oct/Tet Oct/Tet Oct/Tet Oct/Tet

1Ti

+ t/– = * e =*t=

2Ti

,Cr

* t=+t==*t=

3Cr

,Mn

= * t = + t == * t

4Mn

,Fe

= * t * e= * t == * t

5Mn

,Fe

===/

6Fe

2Cb

,Co

3Cc

+ t=– + t

= * e * t

=– * t=

7Co

,Ni

* t=– + t=/*t=

8Ni

,Cu

= * t = + t /= * t

9Cu

= * t * e= * t == * t

Symbols embedded in table have the following meanings: the up and down

arrows indicate positive and negative contributions, respectively; and the t and

e symbols indicate the particular orbital group responsible for the effects

features a trigonal h111i-axis expansion

features a tetragonal h100i-axis contraction or expansion

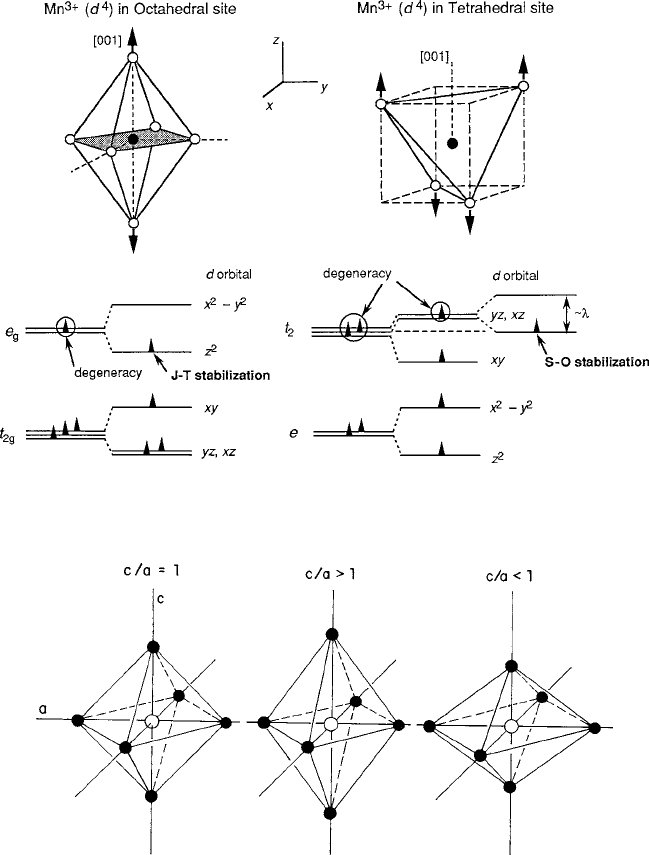
Fig. 5.20 Comparison of a J–T [001]-axis expansion (d

,Mn

) and a S–O [001]-axis

contraction (d

,Co

)

5.3 Magnetocrystalline Anisotropy and Magnetostriction 243

both have the option of stabilizing a singlet or doublet by inducing an axial distortion

either tetragonally or trigonally. In magnetically ordered systems, the spin–orbit en-

ergy can enhance exchange energy through a .L C gm

/  S combination, as

demonstrated by [73]. When   2ı=3 in an exchange ﬁeld of sufﬁcient magni-

tude, stabilization of the doublet is usually the result. Based on a discussion from

Ballhausen [74], the threshold for doublet stabilization in an exchange ﬁeld of en-

ergy E

D gm

is computed in Appendix 5B for the d

.S D 1=2/ case and

determined in (5.79)as[16]









: (5.51)

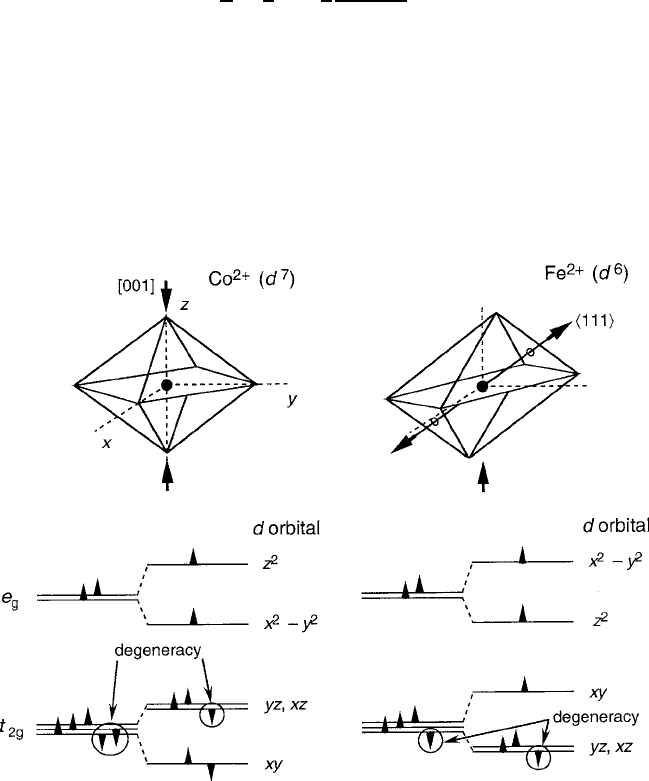
In Fig. 5.21, both Co

and Fe

are depicted with S–O stabilized ground states.

A convenient way to view the Fe

degeneracy is to consider a single hole occupy-

ing the ground doublet. The former case is supported by many measured results that

show a z-axis compression and strong magnetoelastic behavior. The Fe

situation

is less obvious, although Goodenough has pointed out that a trigonal extension is

the result in FeO [75]. Furthermore, the trigonal extension is consistent with the

large 

111

magnetostriction constant observed in spinel ferrites containing ferrous

Fig. 5.21 Comparison of a S–O [001]-axis contraction



; Co



and a S–O [111]-axis

expansion



; Fe



.ForFe

in a tetrahedral site, e.g., ZnO, a J–T [001]-axis contraction could

be expected (see footnote in Sect. 2.4.3)

244 5 Anisotropy and Magnetoelastic Properties

iron ions. Figure 2.13 illustrates the energies of the orbital doublets in the T

and

groups that, respectively, carry the remaining unquenched orbital angular mo-

mentum under the inﬂuence of a tetragonal compression and a trigonal extension.

The independent behavior of the magnetic moments associated with spontaneous

ligand distortions leads one to view them as atomic-scale “domains,” with single-

domain characteristics typical of small crystallites with large K

values, which

will be discussed in the next section. As a consequence, single-ion contributions

to K

can be estimated from the magnitude of the spin–orbit coupling energy.

The method is to assign a spin–orbit energy L  S to each ion when the un-

quenched L of its partially occupied doublet is directed along its preferred (easy)

cubic axis—a compressed h100i in the case of Co

, as envisioned in the sketch of

the .1=



˙ id



degenerate hybrid in Fig. 2.24a. Spin–orbit coupling then

brings the spin vector S to align with L thereby raising the ground-state energy to

L  S cos

,where

is the angle between an easy h100i and the direction of the

ion magnetic moment. Upon referring to Fig. 5.15b, we see that the maximum value

of 

is 55

and cos 

D 1=

3 when the moment is along a hard h111i direction. If

the spins are coupled collinearly, the average anisotropy energy contribution from

one Co

ion will be given by

K

ion

DL  S

1  cos

; (5.52)

where

1  cos

is the average over all equivalent Co

sites, and the net magne-

tization direction in an exchange-ordered system is ﬁxed by the aligned S vectors

parallel to a magnetic ﬁeld.

For the S vectors along a h111i axis each 

D 55

,andK

ion

0:43LS.

If the spontaneous magnetostrictive distortion along the a h100i axis is ignored,

the stabilization of the Co

orbital doublet can also be interpreted as the resultant

effect local trigonal crystal ﬁelds along h111i easy axes at the four equivalent octa-

hedral sites of the host lattice. Slonczewski’s calculations for this scenario compared

favorably with data for Co

-substituted Fe

(magnetite) and show good agree-

ment over a broad temperature range [73]. A more complete analysis might include

crystal-ﬁeld terms for both tetragonal and trigonal ﬁelds with the result that a local

orthorhombic ligand symmetry would appear with a conceivably higher =ı ratio

for greater anisotropy. A similar effect is expected for Fe

because of its likely

spin–orbit stabilization in a trigonal ﬁeld, favoring an extension of the h111i axes.

Here K

has the opposite sign from that of the Co

case but may be lower in

magnitude because of its smaller  constant.

Another ion that could have an orbital degeneracy in the ground state is





in a tetrahedral site is included in Table 5.9. According to the occu-

pancies of the one-electron diagram in Fig. 5.22, the doublet would be stabilized

with a distortion of the same sign as Co

in an octahedral site. However, the

occurrence of Ni

in spinels is almost exclusively in octahedral B sites, where

its magnetoelastic effects should be negligible. Because evidence of anisotropy,

magnetostriction, and spin–lattice relaxation has been associated with the presence

of Ni in NiFe

, the presence of a smaller fraction of the Ni

in the A sublattice

must be considered a strong possibility.

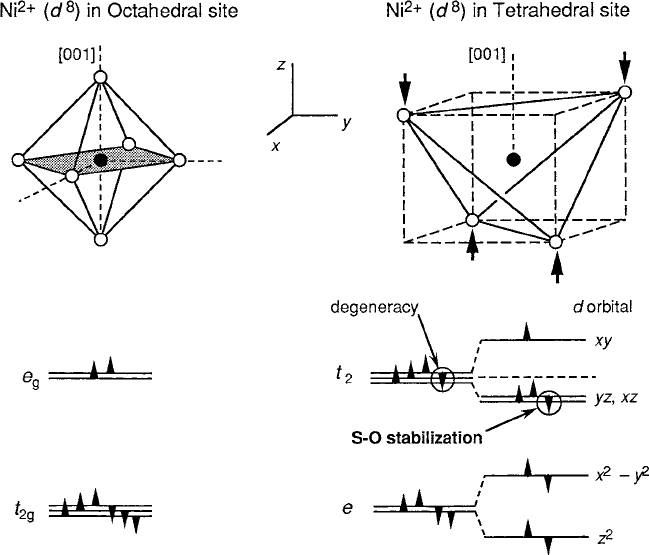
5.3 Magnetocrystalline Anisotropy and Magnetostriction 245

Fig. 5.22 Comparison of spin conﬁgurations of d





in octahedral and tetrahedral sites. In

an octahedral site there are no ﬁrst-order magnetoelastic effects. In the less-common tetrahedral

site, S–O stabilization in the t

triplet could produce both anisotropy and magnetostriction effect

In the J–T case, a singlet with zero orbital angular momentum is lowest, and the

ground state after the spin–orbit coupling operator is applied contains a contribution

of orbital interaction from the hybrid with the excited states. For J–T ions, there-

fore, the magnitude of the anisotropy and spin–lattice interaction of Mn





and Cu





in octahedral sites is determined by the splitting of the E

doublet

in a tetragonal ﬁeld that results from an extension of the apical z axis, sketched in

Fig. 5.23. Because there is no orbital angular momentum associated directly with

the e

states, anisotropy contributions are not expected to be large. Anisotropy re-

sults from second-order contributions from the d

, d

orbitals of the T

shell that

enter the ground state hybrid in the fraction amount =10Dq, which is typically

only a few percent. Although with less probability, both of these ions can occupy

tetrahedral sites and appear to do so in spinel and garnet ferrites. In such cases, the

energy-level order is inverted with the T

term now higher, and small concentra-

tions can undergo spin–orbit stabilization of the l

D˙1 doublet, as sketched in

Fig. 5.24 for Mn





.TheCu

case is analogous, but with an unpaired “hole”

in the T

states. A signiﬁcant feature is that the sign of the ı splitting is the same as

that for the corresponding J–T splitting. As a consequence, the added contribution

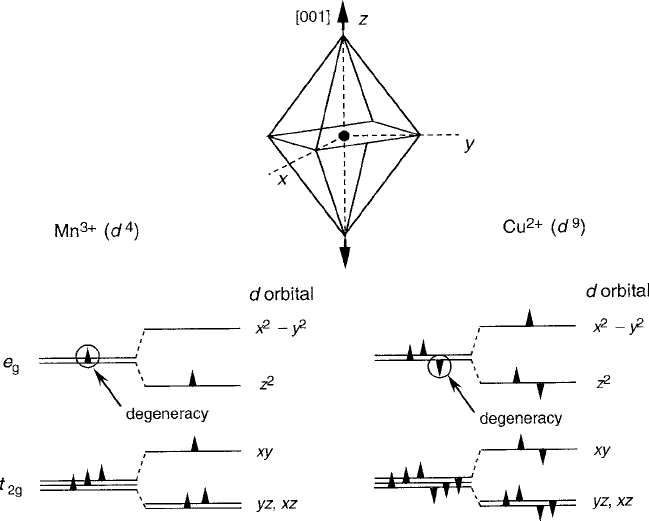
246 5 Anisotropy and Magnetoelastic Properties

Fig. 5.23 Comparison of spin conﬁgurations of classic J–T e

ions d





and d





[001]-axis expansions in octahedral sites

from the tetrahedral sublattice could explain the negative anisotropy and spin–lattice

relaxation enhancements observed in ferrites, as well as the source of magnetic ﬁeld

induced magnetostrictive effects of opposite sign to Co

, listed in Table 5.9 and

discussed in the next section.

5.3.6 Cooperative Single-Ion Effects: Magnetostriction

The single-ion model of anisotropy can also be effective in explaining magnetostric-

tion contributions from isolated sites. For this text, the focus will be on local effects

of magnetoelastically active ions. A scholarly overview of this topic, particularly as

it applies to the magnetic garnets was reported by [76]. Jahn–Teller and spin–orbit

distortions are local, but will inﬂuence the overall lattice strain condition in a man-

ner proposed by Dionne [77]. The “local-site distortion” model of magnetostriction

provides an useful qualitative guide to the properties of spinel and garnet ferrite

compounds where the highly magnetoelastic individual ions can signiﬁcantly al-

ter the magnetostriction of the iron-dominated sublattices. Local-site distortions are

sketched for h100i and h111i axes in Figs. 5.25 and 5.26.Fortheh100i distortion

5.3 Magnetocrystalline Anisotropy and Magnetostriction 247

Fig. 5.24 Comparison of spin conﬁgurations of d





[001]-axis expansions in octahedral

and tetrahedral sites. Note that the stabilization is J–T in the octahedral case, but S–O in the infre-

quent tetrahedral case

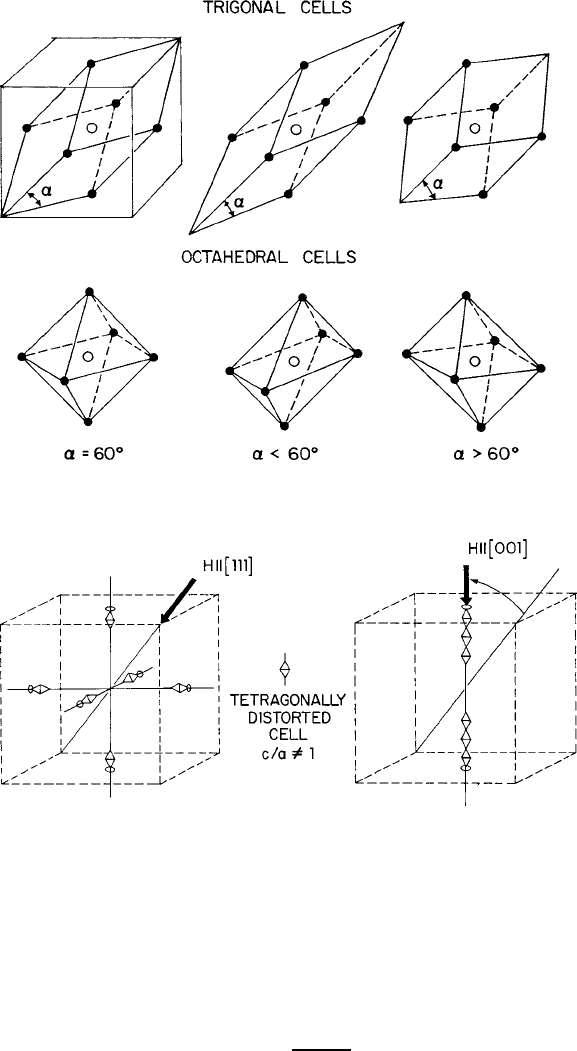
Fig. 5.25 Octahedral sites with tetragonal distortion along [001] axis. Figure reprinted from [77]

with permission.

 1979 by the American Institute of Physics

case, in the unmagnetized state the cube edge length parameter l

100

undergoes local

changes of l

100

that are equally distributed among the three equivalent h100icrys-

tallographic axes. As M is aligned with the h100iaxis, all three groups of distortions

can become cooperative, thereby producing a combined 3l

100

change along the

h100i axis sketched in Fig. 5.27.IfM is then rotated to a h111i axis, the individual

248 5 Anisotropy and Magnetoelastic Properties

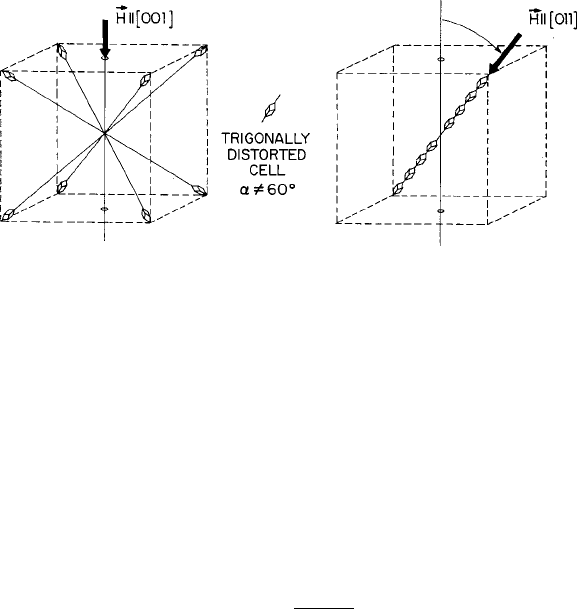
Fig. 5.26 Lattice sites with trigonal distortion along [111] axis. Figure reprinted from [77] with

permission.

 1979 by the American Institute of Physics

Fig. 5.27 Site former that the local distortion < 100> axis of each site will align with the ﬁnal H

direction to create a resultant magnetostrictive strain along the [001] axis. Figure reprinted from

[77] with permission.

 1979 by the American Institute of Physics

site distortions will relax back to their respective h100i axes, producing no ﬁrst-

order change in the l

111

parameter. The single-ion magnetostriction constants can

then be expressed as



site

100

3l

100

5.3 Magnetocrystalline Anisotropy and Magnetostriction 249

Fig. 5.28 Site distortion switching as H is rotated from the [001] axis to the [111] axis. Diagram

is intended to convey that the local distortion <111> axis of each site will align with the ﬁnal H

direction to create a resultant magnetostrictive strain along the [111] axis. Figure reprinted from

[77] with permission.

 1979 by the American Institute of Physics



site

111

D 0: (5.53a)

This result predicts a l

100

extension for a Mn





ion in either type of cubic

site. For the h100i compression typical of Co

in an octahedral site (and Ni

a tetrahedral site) the sign of 

100

is reversed. In the case of Fe

in an octahedral

site (Fig. 5.26), four h111i distortions diagonals cooperate to make resultant 4l

111

extension sketched in Fig. 5.28, and the relations between 

100

and 

111

are



site

100

4l

100



site

111

D 0: (5.53b)

The impetus for aligning the distorted sites comes from the local spin–orbit gener-

ated anisotropy, which, as discussed above, is greater for d

and d

than for the pure

J–T d

and d

cases. An example of experimental data for these cases in ferrimag-

netic oxides is presented in Fig. 5.29. Through the use of controlled substitutions of

local-site distortion ions, anisotropy, and magnetostriction can be tailored to produce

a range of properties. Qualitative summaries of the more common spinel and gar-

net systems are given earlier in Tables 4.5 and 4.6. Quantitatively, K

values are

several times greater for spinels than garnets, typically in the range of 150–300 Oe.

Magnetostriction in the spinels is also larger, particularly the 

100

constant which

is typically 25 10

6

in contrast to values of 2 10

6

for YIG. Nickel ferrite

NiFe

has a 

100

50  10

6

. Ratios of 

, however, are more compa-

rable. If rare-earth ions occupy the garnet c sublattice in sufﬁcient concentrations,

both K

and 

increase, as determined by Iida [78].

The importance of magnetoelastic parameters can be seen in the shape of hys-

teresis loops, which will be reviewed in the next section, and in the microwave

propagation properties to be discussed in Chap. 6.

250 5 Anisotropy and Magnetoelastic Properties

Fig. 5.29 Variation in the room-temperature magnetostriction constants of yttrium–iron garnet

with Mn

concentration. Note that hiD

. Figure reprinted from [77] with permission.

 1979 by the American Institute of Physics

5.4 Magnetization Process and Hysteresis

Local magnetoelastic effects reveal themselves most commonly in the magneti-

zation process, particularly in relation to hysteresis. These occasions frequently

involve ferrites, usually in polycrystalline form. The ability to create a state of

magnetization with minimum energy deﬁnes a “soft” magnetic material; the abil-

ity to retain the magnetized state under conditions of maximum demagnetizing

inﬂuences determines a “hard” magnetic material. Except for a superﬁcial intro-

duction in Sect. 1.1.4, we have so far ignored the role of magnetic domains largely

because domains are the features of the partially magnetized state. Since the empha-

sis has been on single-ion moments and the establishment of the fully magnetized