Deza M.M., Laurent M. Geometry of Cuts and Metrics

268

Chapter

17.

Hypermetric

Graphs

nodes

at

distance

1 from i

and

distance

m + 1 from

j.

Hence, G is

regular

with

valency b

o

and

there

are k

m

nodes

at

distance

m from

any

node

i E V(G),

where

ko

= 1,

kl

= 1, km+l =

~::~,

m

2:

O.

Let

J-L

denote

the

number

of

common

neighbors

of

two nodes

at

distance

2,

i.e.,

J-L

= C2. A strongly regular

graph

is a

distance-regular

graph

of

diameter

2.

Note

that

the

quantity

LiEV(C)

dc(i,j)

=

Lm?omkm

does

not

depend

on

j E X for a

distance-regular

graph.

Hence,

we

can

derive

the

following

result

(e.g., from

Theorem

6.2.18).

Proposition

17.2.6.

For a distance-regular graph G, the following are equiva-

lent.

(i)

G is

of

negative type.

(ii)

The

graphic

metric

space (V(G),

dc)

has a spherical representation.

(iii)

The

distance

matrix

Dc

has exactly one positive eigenvalue.

I

Koolen

and

Shpectorov

[1994] have completely classified

the

distance-regular

graphs

of

negative

type.

We

present

below

their

classification;

we

refer, e.g.,

to

Brouwer,

Cohen

and

Neumaier

[1989] for

the

description

of

the

graphs

not

defined here.

Theorem

17.2.7.

Let

G

be

a distance-regular graph. Then, G is

of

negative

type

if

and

only

if

one

of

the following holds.

(i)

J-L

=

2n

- 2

and

G is a cocktail-party graph K

nx2

.

(ii)

J-L

= 10

and

G is the Gosset graph G

56

•

(iii)

J-L

= 8

and

G is the Schlafii graph G

27

•

(iv)

J-L

= 6

and

G is a half-cube graph

~H(n,

2)

(n

2:

4).

(v)

J-L

= 4

and

G is

one

of

the three Chang graphs.

(vi)

J-L

= 4

and

G is a

Johnson

graph

J(n,

d)

(d

2:

2).

(vii)

J-L

= 2

and

G is a

Hamming

graph

H(n,

d)

(=

(Kd)n)

(n, d

2:

2).

(viii)

J-L

= 2

and

G is a Doob graph (including the Shrikhande graph).

(ix)

J-L

= 2

and

G is the icosahedron graph.

(x)

J-L

= 1

and

G is the dodecahedron graph.

(xi)

J-L

= 1

and

G is the

Petersen

graph.

(xii)

J-L

= 1

and

G is a circuit

en.

(xiii)

J-L

= 1

and

G is a double-odd graph

D0

2n

+l'

(xiv)

J-L

= 0

and

G is a complete graph

Kn.

I

17.3

Extreme

Hypermetric

Graphs

269

In

fact, all

the

graphs

listed in

Theorem

17.2.7 are hypermetric. Therefore,

Corollary

17.2.8.

A distance-regular graph is hypermetric

if

and

only

if

it

is

of

negative type, i.e.,

if

it

is one

of

the graphs (i)-(xiv). I

Therefore,

the

metric hierarchy from

Theorem

6.3.1

partially

collapses for

distance-regular graphs;

we

will see in

Theorem

19.2.8

that

it also does for con-

nected

bipartite

graphs.

Note

that

all

the

graphs

listed in

Theorem

17.2.7,

with

the

exception

of

G

27

,

G

56

and

the

three

Chang

graphs, are £l-graphs and, if

we

exclude moreover Knx2

for n

:2:

5,

all

of

them

are isometric

subgraphs

of a half-cube

graph.

Hence,

Corollary

17.2.9.

Let

G

be

a distance-regular graph.

(i) G is

an

£l-graph

if

and

only

if

G is one

of

the graphs from (i), (iv), or

(vi)-(xiii).

(ii)

G is

an

isometric

subgraph

of

a half-cube graph

if

and

only

if

G is one

of

the graphs

from

(iv), (vi)-(xiv).

(iii)

G is

an

isometric

subgraph

of

a hypercube graph

if

and

only

if

G is a

double-odd graph

D02n+l, a hypercube

H(n,

2),

or

an

even

circuit 02n.

(iv) Suppose

that

G

be

a strongly regular graph. Then, G is

hypermetric

if

and

only

if

G is Kn x K

n

,

J(n,2),

Knx2,

!H(5,2),

G

27

, the 5-circuit 0

5

,

the

Petersen

graph, the Shrikhande graph,

or

one

of

the three Chang graphs.

I

The

assertion (ii) was

obtained

by Shpectorov

[1996];

(iii)

can

be found

in

Koolen

[1990]

and

in

Weichsel [1992];

and

(iv)

in

Koolen

[1990]

and

in Deza

and

Gr-

ishukhin [1993].

Further

results concerning

the

distance-regular

graphs

satisfying

some subclass

of

hypermetric

inequalities (such as, for instance,

the

pentagonal

inequalities, or

the

6-gonal inequalities)

can

be found

in

Koolen [1990, 1994].

17.3

Extreme

Hypermetric

Graphs

In

this

section,

we

consider

extreme

hypermetrics arising graphs, i.e.,

the

graphs

G whose

path

metric

do

(or whose

truncated

distance

do)

lies

on

an

extreme

ray

of

the

hypermetric

cone.

We

remind

that

G

is

said

to

be

hypermetric

when

its

path

metric

is

hypermetric. All

the

results presented here are

taken

from Deza

and

Grishukhin

[1993].

Let

G

be

a

hypermetric

graph. Let

Po

denote

the

Delaunay

polytope

asso-

ciated

with

the

hypermetric

space (V(G),

2do)

and

let

Ho

denote

its

I-skeleton

graph.

Hence,

Po

is

a Delaunay

polytope

in a

root

lattice

and

G

is

an

iso-

metric

subgraph

of

Ho.

Moreover, G

is

an

extreme

hyper metric if

and

only if

P

is

an

extreme

Delaunay

polytope

(by

Theorem

15.1.8).

By

Theorem

16.0.1,

the

only

extreme

Delaunay polytopes

in

a root lattice are

the

segment

£Xl,

the

270

Chapter

17. Hypermetric Graphs

Schliifli polytope

221

and

the

Gosset polytope

321'

Therefore, if G is

an

extreme

hypermetric

graph

distinct from

K2,

then

we

are in one

of

the

following two

situations:

(i)

Either

HG

G

56

, i.e., G is

an

isometric subgraph of G

56

which

is

gen-

erating

(Le.,

V(G)

viewed as subset

of

the set of vertices V(3

2

d of 3

21

generates V(321));

we

then

say

that

G is an extreme hypermetric graph

of

Type

1.

(ii)

Or

HG

= G

27

, Le., G is an isometric subgraph of

G27

which is generating

(i.e.,

V (G) generates V

(2

21

));

we

then

say

that

G

is

an

extreme hypermetric

graph

of Type

II.

A generating subset in

G27

has

at

least 7 elements.

We

found

that

there

are

26

distinct

(up

to

permutation) generating subsets in G

27

with

7 elements

(i.e., basic subsets of 2

21

;

see Section 16.2). For B

~

V(G

27

),

recall

that

G27[B]

denotes

the

subgraph of G

27

induced by

B.

Note

that

G27[B]

is

an

isometric

subgraph of

G27

if and only if G

27

[B]

has diameter 2 and, in this case,

G27[B]

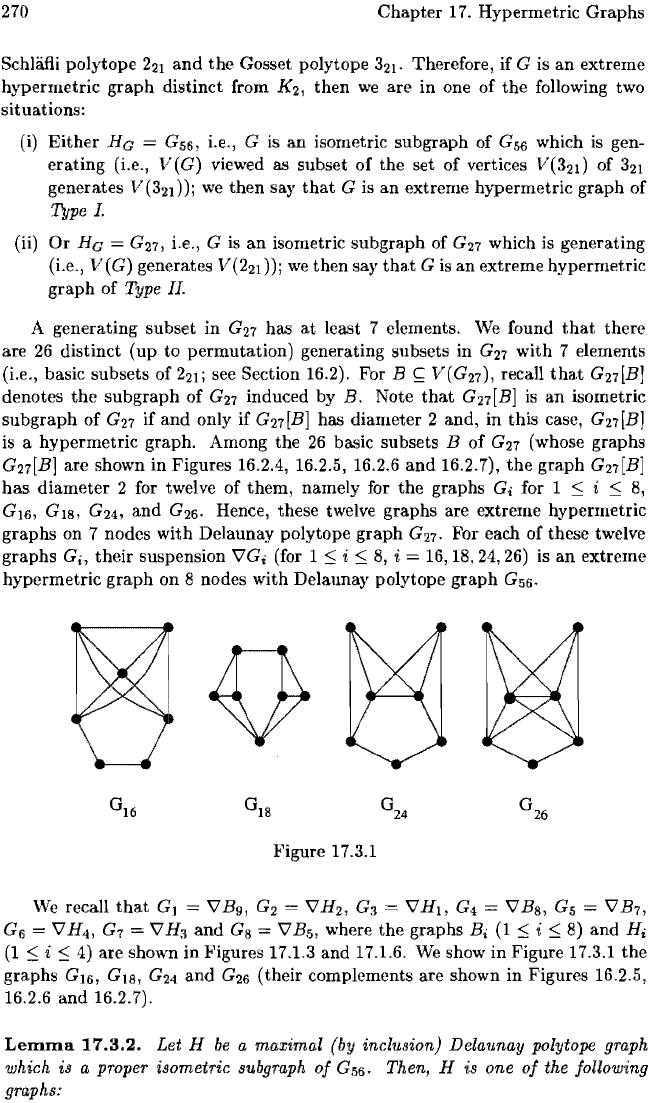
is a hypermetric graph. Among the

26

basic subsets B

of

G27

(whose graphs

G27[B]

are shown in Figures 16.2.4, 16.2.5, 16.2.6

and

16.2.7),

the

graph

G27[B]

has

diameter 2 for twelve

of

them, namely for the graphs Gi for 1

:::;

i

:::;

8,

G

16

, GIS, G

24

, and G

26

. Hence, these twelve graphs are extreme hypermetric

graphs on 7 nodes with Delaunay polytope

graph

G

27

. For each of these twelve

graphs

Gil their suspension 'ilG; (for 1

:::;

i

:::;

8,

i = 16,18,24,26) is

an

extreme

hypermetric

graph

on 8 nodes with Delaunay polytope

graph

G

56

.

Figure 17.3.1

We

recall

that

G] 'ilB

g

,

G

2

'ilH

2

, G

3

= 'ilH

1

,

G

4

= 'ilBs, G

5

= 'ilB7,

G

6

'il

H

4

,

G7

=

'il

H3

and

Gs

'il

Bs, where

the

graphs Bi

(1

:::;

i S

8)

and

Hi

(1:::;

i:::;

4) are shown in Figures 17.1.3 and 17.1.6.

We

show in Figure 17.3.1 the

graphs

G16,

GI8,

G24

and

G26

(their complements are shown in Figures 16.2.5,

16.2.6

and

16.2.7).

Lemma

17.3.2.

Let

H

be

a

maximal

(by inclusion) Delaunay polytope graph

which is a proper isometric subgraph

of

G56.

Then, H is

one

of

the following

graphs:

17.3

Extreme

Hypermetric Graphs

(i) H = J(8, 2).

(ii) H = K

6x2

X K

2

•

(iii) H =

!H(6,2).

(iv) H = G

27

•

271

Proof.

We

know

that

H is a direct product of

the

Delaunay polytope graphs from

Figure 14.3.1. Let

r denote the radius of the Delaunay polytope whose I-skeleton

graph

is

H.

Then,

r2

:::;

~,

since H is contained in

GS6.

(We remind

that,

for

two graphs

HI

and

H

2

,

Hl

'-;

H2

means

that

HI is an isometric subgraph of

H2.)

•

If

H =

J(n,

t),

then

r2

t(:-t):::;

~,

implying

that

t

1,2,3.

Then, H is not

maximal except

for

J(8,2). Indeed,

if

t 1,

then

n

:::;

7 and Kn

'-;

J(8,2); if

t = 2,

then

n

:::;

8

and

J(n,2)

'-;

J(8, 2); if t = 3,

then

n = 6 and J(6, 3)

'-;

!H(6,

2).

•

If

H = Knx2'

then

n

:::;

6

and

Knx2

'-;

K

6X2

X K

2

.

•

If

H

!H(n,2),

then

r2

=

~

:::;

!,

implying

that

n

:::;

6 and thus H

'-;

!H(6,2).

Else H G

27

or

H is a direct product. Suppose

that

H = HI X H

2

.

Denote

by

rI,

r2

the

radius

of

the

Delaunay polytope whose I-skeleton

graph

is

HI,

H

2

,

respectively.

r2

rf

+

r~

:::;

~.

Looking

at

the

radii of the Delaunay

polytopes from Figure 14.3.1,

it

is easy

to

see

that

the

only possibility is Hl =

K6x2,

H2

K2

H

1,

ri

~)

(for instance, for HI =

H2

= K

4

,

ri

=

ri

=

~

but

K4

X

K4

'-;

J(8,2».

I

Lemma

17.3.3.

Let

H

be

a maximal (by inclusion) Delaunay polytope graph

which is a proper isometric subgroph

of

G

27

. Then, one

of

the following holds.

(i) H J(6, 2).

(ii) H

= K5x2.

(iii) H

!H(5,2).

(iv) H = K6.

Proof.

The

proof is similar to

that

of Lemma 17.3.2.

We

use

the

fact

that

the

radius r of

the

Delaunay polytope whose I-skeleton graph is H satisfies

1'2

:::;

t.

It

is easily seen

that

H cannot

be

a direct product.

•

If

H =

J(n,

t),

then

1'2

=

t(:-t)

:::;

!,

implying

that

t =

1,2

and n

:::;

6. Hence,

we have (i) or (iv).

•

If

H = Knx2'

then

n

:::;

5 (because K

6x2

is not contained in G

27

) and

thus

H,-;

K

5x2

.

•

If

H =

tH(n,2),

then

r2 =

~

:::;

!,

implying

that

n

:::;

5 and thus H

'-;

!H(5,2).

I

272

Chapter

17.

Hypermetric

Graphs

We deduce

the

following characterization for

extreme

hypermetric

graphs.

Proposition

17.3.4.

Let

G

be

a connected graph distinct from K

2

•

Then, G is

an extreme hypermetric graph

if

and only

if

one

of

the following assertions hold.

(I) G is an

isometric

subgraph

of

G

56

and G is

not

an

isometric

subgraph

of

J(8,2),

K

6x2

x K

2

,

~H(6,

2)

or G

27

•

(II) G is an isometric subgraph

of

G

27

and G is

not

an isometric subgraph

of

K

5x2

,

J(6,2),

K6

or

~H(5,

2).

I

Observe

that

all

the

excluded graphs

in

Proposition

17.3.4 are

~'l-graphs.

In

other

words, every isometric

subgraph

of

G

56

is either

an

extreme

hypermetric

graph

or

an

£l-graph.

As

an

application

of

Proposition

17.3.4,

we

obtain

that:

• Every isometric

subgraph

of

G

27

on

n

:::::

17 nodes

is

extreme.

•

Every

induced

subgraph

of G

27

on

n

:::::

20

nodes

is

extreme

(since deleting

7 nodes from G

27

preserves

the

diameter

2 because

Jl(

G

27

) = 8).

• Every isometric

subgraph

of

G

56

on

n

:::::

33 nodes

is

extreme.

• Every induced

sub

graph

of

G

56

on

n

:::::

47 nodes is

extreme

(since

Jl(

G

56

) =

10).

•

If

G is a connected

graph

of

diameter

2,

then

its suspension

\lG

is

an

extreme

hypermetric

graph

of

Type

I if

and

only if G is

an

extreme hyper-

metric

graph

of

Type

II.

Let us finally collect some properties for

the

extreme

hypermetric

spaces

arising from

the

graphs G E

LBGS.

As

we

saw

in

Section 17.2, if G

is

a connected regular

graph

with

Amin(Ac)

:::::

-2,

then

its

truncated

distance

de

is

hypermetric. Let P

a

denote

the

Delaunay

polytope

associated

with

(V(G),

2d

e

)

and

let

He

denote its I-skeleton

graph.

Suppose

that

G belongs to

the

class

LBGS;

that

is, G is connected regular

with

Amin(Ac)

:::::

-2

and

G is

not

a line

graph

nor a cocktail-party graph. By

Remark

17.2.5,

He

is

one

of

J(6, 3),

~H(5,

2),

~H(6,

2), G

27

or G

56

. Since (V(G),

de)

is

an

isometric subspace

of

(V(He),

d

Ha

) which, in

turn,

is

an

isometric subspace

of

(V(G56),dcs6)'

we

deduce

that

G does

not

contain

any

pair

of

nodes

at

distance

3

in

G

56

;

in

particular,

if

G

is

an

induced

sub

graph

of

~H(6,

2),

then

G has

at

most

n

:::;

16

nodes. Hence,

Proposition

17.3.5.

Let G

be

a graph

of

LBGS.

If

G is

not

an induced sub-

graph

of

~H(6,

2), then

de

is extreme hypermetric.

In

particular,

if

G has n

:::::

17

nodes, then

de

is extreme hypermetric. I

17.3

Extreme

Hypermetric

Graphs

273

Proposition

17.3.6.

(i)

A graph G E

£BGS

is extreme hypermetric

if

and only

if

it

has diameter 2

and

it

is

not

an

induced subgmph

of

tH(6,

2).

(ii)

Every

extreme hypermetric graph which is regular and has diameter 2

be-

longs to

£BGS.

(iii)

Let

G

be

an extreme hypermetric graph from then, G is

of

Type I

(resp.

of

Type II)

if

and only

if

G belongs to the layer

£1

(resp. £2).

(iv) Every graph from

£BGS

on n

?:':

17 and with valency k

?:':

9 is an extreme

hypermetric graph. They are the

29

graphs

in

layer

£1

numbered

NN135-

163 and the 8 graphs

in

layer £2 numbered NN177 184.

(v)

All

the nine maximal (by inclusion) graphs

of

£BGS

are extreme hyper-

metric graphs; they are the Schliifli graph

G21

(numbered N184), the three

Chang graphs

NN161

163, and the five graphs NN148

152

on

22

nodes.

I

Part

III

Isometric

Embeddings

of

Graphs

Introduction

In

Part

III,

we

study

various embeddability properties

of

graphs. A metric space

can

be

attached

to

any connected

graph

in

the following way.

Let

G =

(V,

E)

be

a

connected graph.

Its

path

metric

dG

is

the metric defined on V by

letting

dG(a,

b)

denote

the

length

of

a

shortest

path

joining a

to

bin

G, for all nodes a, b E

V.

Then,

(V, dG)

is

a metric space, called the graphic

metric

space associated

with

G.

The

distance

matrix

of

G is

the

matrix

DG (dG(a, b))a,bEV'

\Ve

have seen

in

Part

I a hierarchy

of

metric properties

that

a given

distance

space may enjoy;

in

particular,

isometric embeddability into

the

hypercube

and

into

the

Banach

£1-,

£2-spaces, hypermetricity,

and

the

negative

type

condition.

Vve

study

here

the

graphs whose

path

metric enjoys some

of

these properties.

Accordingly, a

graph

G

is

called

an

£l-graph, a hypercube embeddable graph, a

hypermetric

graph, a graph

of

negative type,

if

its

path

metric

dG

is

isometrically

£l-embeddable, hypercube embeddable, hypermetric, of negative type, respec-

tively.

Given two connected graphs G

and

H,

we

write

and

say

that

G

is

an

isometric

subgraph (or, distance-preserving

subgraph)

of

H

if

there

exists a

mapping

a:

V(G)

----->

V(H)

such

that

dH(a(a),

a(b)) = dG(a,

b)

for all nodes

a,

b E V (G).

We

will consider

in

Part

III

in

particular

the

cases

when

the

host

graph

H is a hypercube (see

Chapter

19), a

Hamming

graph

or,

more generally, a

Cartesian

product

of

irreducible graphs (see

Chapter

20).

Several

other

weaker types

of

embeddings of graphs have

been

considered

in

the

literature.

For instance, one may consider

the

graphs G

that

can

be

em-

bedded

into H as

an

induced subgraph; such embeddings are called topological

embeddings

and

will

not

be considered here.

An

even weaker

notion

of

embed-

ding

consists of asking which graphs G

can

be embedded into H as a

(partial)

subgraph,

i.e., requiring only

that

the

edges be preserved; see Section 19.3 where

the

case of

the

hypercube as host

graph

H is briefly discussed.

278

Introduction

The

theory

of

isometric embeddings of

graphs

is a rich theory,

with

many

applications.

The

main

goal is

to

try

to

embed

graphs

isometrically

into

some

other

simpler

graphs. Research

in

this

area

was

probably

motivated

by a

problem

in

communication

theory

posed

by Pierce [1972].

In

a telephone network one

wishes

to

be

able

to

establish

a connection between two

terminals

A

and

B

without

B knowing

that

a message is on its way.

The

idea

is

to

let

the

message

be

preceded

by some "address"

of

B,

permitting

to

decide

at

each node

of

the

network

in

which

direction

the

message

should

proceed. Namely,

the

message

will proceed

to

the

if

its

Hamming

distance

to

the

destination

node

B is

shorter.

The

most

natural

way

of

devising such a scheme is by labeling

the

nodes by

binary

strings, which

amounts

to

try

to

embed

the

graph

in

a

hypercube.

Unfortunately, not all

graphs

can

be

embedded

into

hypercubes. We

study

in

detail

in

Chapter

19

the

hypercube

embeddable

graphs. We

present

their

basic

structural

characterization,

due

to

Djokovic

(Theorem

19.1.1),

and

some

other

equivalent characterizations

(Theorems

19.2.1, 19.2.5

and

19.2.8).

The

notion

of

isometric

embedding

into

hypercubes

can

be

relaxed

in

several

ways.

First,

one

may

consider isometric

embeddings

into

squashed

hypercubes

as

in

Graham

and

Pollack [1971]. Namely, one tries

to

label

the

nodes by sequences

using

the

symbols

"0,1,

*",

with

the

distance

between

x,

y E

{O,

1,

*}

being

equal

to

1

if

{x,y}

=

{0,1}

and

to

° otherwise.

It

turns

out

that

every connected

graph

on

n nodes

can

be

isometrically

embedded

into

the

squashed

hypercube

of

dimension

n - 1

(Winkler

[1983]). (Note

that

the

squashed

hypercube

is

not

a

semimetric

space.)

One

may

also consider isometric

embeddings

into

arbitrary

Cartesian

prod-

ucts.

In

fact, every connected

graph

admits

a unique canonical isometric em-

bedding

into

a

Cartesian

product

whose factors are irreducible

(Graham

and

Winkler

[1985]).

This

result

together

with

some applications is

presented

in

Chapter

20.

Another

way

of

relaxing isometric

embed

dings

into

hypercubes

is

to

look for

isometric

embeddings

into

hypercubes

up

to scale, i.e., to consider £l-graphs;

such

embeddings

were first considered

in

Blake

and

Gilchrist [1973].

Chapter

21

contains

results

on

£l-graphs;

among

them,

a

polynomial

time

algorithm

for

recognizing

£l-graphs

and

a

structural

characterization

for isometric

subgraphs

of

half-cube graphs.

M.M. Deza, M. Laurent, Geometry of Cuts and Metrics, Algorithms and Combinatorics 15,

Chapter

18.

Preliminaries

on

Graphs

We

introduce

here several notions

about

graphs

and

embeddings,

that

we will

need

in

Part

III. We

start

with

defining a

certain

relation 0 on

the

edge

set

of

a

graph,

which leads

to

the

notion

of

isometric dimension

of

the

graph.

Let G

=

(V,

E)

be

a graph.

Each

edge

(a,

b)

of

G induces a

partition

of

the

node

set

V

of

G into

where

(18.0.1)

V = G(a,

b)

U G(b,

a)

U G=(a,

b),

{

G(a,

b)

G(b,

a)

G=(a,

b)

:=

{x

E V I

de(x,a)

<

dc(x,b)},

:=

{x

E V I

de(x,

b)

<

dc(x,

a)},

:=

{x

E V I

de(x,

a)

=

de(x,

b)}.

Clearly,

if

G is a

bipartite

graph,

then

G=(a,

b)

= 0 for each edge

(a,

b)

of

G.

The

following relation

0,

defined on

the

edge

set

of

a graph, was first in-

troduced

by

Djokovic [1973].

It

plays a crucial role

in

the

theory

of

isometric

embed

dings

of

graphs. Given two edges e =

(a,

b)

and

e'

=

(a',

b')

of

G, let

(18.0.2)

e 0

e'

if

dc(a',

a)

- dc(a',

b)

of-

de(b',

a)

- de(b',

b).

In

other

words, e' is

in

relation by 0

with

e

if

the

edge e' "cuts"

the

partition

V = G(a,

b)

U G(b,

a)

U G=(a,

b)

induced by

the

edge

e,

i.e.,

if

the

endpoints

of

e' belong

to

distinct

sets

in

this

partition.

The

relation 0 is clearly reflexive

and

symmetric,

but

not

transitive

in

general. For instance, 0

is

not

transitive

if

G is

the

complete

bipartite

graph

K2,3.

Actually,

the

relation 0 is transitive

precisely

when

the

graph

G

can

be isometrically embedded into (K3)m for some

m

::::

1 (see Corollary 20.1.3).

The

transitive closure

of

0

is

denoted

by

0*.

The

number

of

equivalence classes

of

0*

is called

the

isometric

dimension

of

G

and

is

denoted

by

dimJ(G).

As will

be

seen in

Chapter

20,

every connected

graph

G

can

be

embedded

in

a canonical way in a

Cartesian

product

of

dimJ(G) irreducible

graphs.

We now recall further definitions needed

in

Part

III. Given two sequences

x = (Xl,

...

, x

m

), Y = (YI,

...

,Ym) E

~m,

their

Hamming

distance

dH(X,y)

is

defined

by

dH(x,y)

= I{i E {I,

...

,m}

I

Xi

of-

ydl·

Deza M.M., Laurent M. Geometry of Cuts and Metrics

Подождите немного. Документ загружается.