Deza M.M., Laurent M. Geometry of Cuts and Metrics
Подождите немного. Документ загружается.

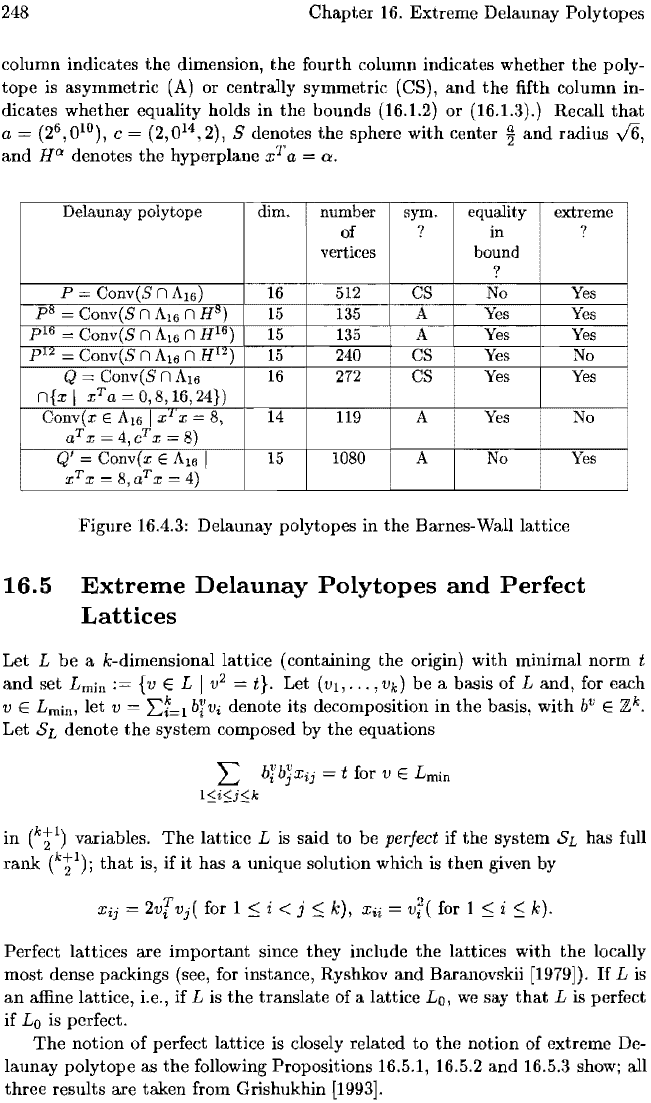
248
Chapter
16.
Extreme Delaunay Polytopes
column indicates the dimension, the fourth column indicates whether the poly-
tope is asymmetric (A) or centrally symmetric
(CS),
and
the
fifth column in-
dicates whether equality holds in the bounds (16.1.2) or (16.1.3).} Recall
that
a =
(2
6
,0
1
°), c (2,0
14
,2),
S denotes
the
sphere
with
center
~
and
radius
.16,
and
HCX
denotes the hyperplane x
T
a
a.
Delaunay
polytope
dim.
number
sym.
equality
extreme
of
?
in
?
vertices
bound
?
p =
Conv(S
n A
16
)
16
-=m=r
CS
No
Yes
po
=
Conv(S
n Al6 n
H")
15
A
Yes Yes
PLO
=
Conv(S
n Al6 n
H<D)
15
135
A Yes Yes
pl~
=
Conv(S
n Al6 n
Hl~)
I.5
240 CS Yes
No
Q
Conv(S
nA
16
16
272 CS
Yes Yes
n{xl
x
T
a=0,8,16,24})
Conv(x
E Al6 I
Xl
X - 8,
14
119
A Yes No
aTx
=
4,c
T
x
= 8)
Q'
Conv(x
E
AlB
I
15
1080
I
A No Yes
xTx
=
8,a
T
x
=
4)
Figure 16.4.3: Delaunay polytopes in the Barnes-Wall lattice
16.5
Extreme
Delaunay
Polytopes
and
Perfect
Lattices
Let L
be
a k-dimensionallattice (containing the origin) with minimal norm t
and
set Lrnin
:=
{v
ELI
v
2
= t}. Let
(Vi,
...
,Vk)
be
a basis
of
L and, for each
V E Lrnin, let V
I:tl
bivi
denote
its
decomposition in
the
basis, with b
V
E71}.
Let SL denote
the
system composed by
the
equations
2::
bibjxij
= t for v E Lmin
l~i~j~k
in (ktl) variables.
The
lattice L is said to
be
perfect if
the
system SL has full
rank
(ktl);
that
is, if
it
has a unique solution which is
then
given by
Xij
= 2vT
Vj(
for 1
::;
i < j
::;
k),
Xii
v;( for 1
::;
i
::;
k).
Perfect lattices are
important
since they include
the
lattices with
the
locally
most dense packings (see, for instance, Ryshkov
and
Baranovskii [1979]).
If
Lis
an
affine lattice, i.e., if L is
the
translate of a lattice Lo,
we
say
that
L is perfect
if
Lo is perfect.
The
notion
of
perfect lattice is closely related to the notion of extreme De-
launay polytope as
the
following Propositions 16.5.1, 16.5.2
and
16.5.3 show; all
three results are taken from Grishukhin [1993].

16.5
Extreme
Delaunay Polytopes
and
Perfect Lattices
249
Proposition
16.5.1.
Let
P
be
a
Delaunay
polytope with radius
r,
let
Lo
denote
the lattice generated by
the
set
of
vertice.9
V(P)
of
P
and
let t denote its
mini-
mal
norm.
Suppose
that
P is a basic extreme Delaunay polytope,
that
there exist
u,v
E
V{P)
with (u v)2 t
and
that t
ir2.
Then, there exists w
not
lying
on
the affine space spanned by P
such
that
(w
-
v)2
= t
for
all v E
V(P)
and
such
that
the lattice L generated by Lo U {w} is perfect.
Proof.
We
can suppose
without
loss
of
generality
that
the
origin is a vertex
of
P. By
Lemma
14.4.5,
the
spherical t-extension
of
the
space
(V(P),d(2))
has a
spherical
Let
w denote
the
vector representating
the
extension
point. So,
(w
2::
t for all v E
Lo
with
equality
if
v E
V(P).
Let L denote
the
lattice
by
LoU{w}.
Then,
L
UaEzLa,
where
La:=
(Lo+aw)
are
the
layers composing
L.
The
distance between two consecutive layers is h =
vt
-r2.
We
check
that
the
minimal
norm
of
L is equal
to
t, i.e.,
that
v
2
2::
t for all
v
L,
v
=1=
O.
This
is obvious
if
v lies in Lo.
If
v lies
in
a layer La which is
not
consecutive
to
the
layer L
o
,
then
Ilv
112::
2h, i.e.) v
2
2::
4h2 =
4(t
- r2)
2::
t since
t .
If
v lies
in
a layer consecutive
to
Lo, say v = u - w where u E L
o
,
then
t.
Since P is basic,
we
can
find a basis
(Vb'
..
,Vk)
of
Lo
composed
of
vertices
of
P.
Then,
(w,
Vb
...
,Vk)
is a basis
of
L.
So,
the
system S L is composed by
the
equations:
We show
that
SL has full rank. Let x denote a solution
of
SL'
Since
w,
w -
VI,
.••
) w - Vk E L
min
,
we
deduce
that
the
equations:
Xoo
= t,
xoo
+
Xii
-
XOi
= t
(1
:"::
i
:"::
k)
belong
to
SL' Therefore,
Xoo
= t and
Xii
=
XOi
for i 1,
...
,
k.
Let
V E
V(P),
V =
Ll:;i9
b'/vi
with
b
V
E Zk.
Then,
v -
wE
Lmin, implying
the
equation:
Xoo
- L
b,/XOi
+ L b'(bjxij
1:;i:;k
1:;i:;j9
of
S
L.
Hence, x satisfies
(a)
for each v E
V(P).
L ((bn
2
bi)xii +
l:;i:;k
By
assumption, P
is
an
extreme Delaunay polytope;
that
is,
the
system
S(V(p),d(2)),
composed by
the
equations:
(b)
L
bj)b~doi
+
l~j$:k
o

250
Chapter
16.
Extreme
Delaunay Polytopes
Set
d
Oi
Xii
for 1
:::;
i
:::;
k
and
d
ij
:=
Xii
+
Xjj
2Xij
for 1
:::;
i < j
:::;
k.
Then,
since X satisfies (a),
we
deduce
that
d satisfies (b). Therefore, d
is
uniquely
determined
up to multiple. This implies
that
X too is uniquely determined
up
to
multiple.
The
fact
that
there exist u, v E
V(P)
with u - v E Lmin permits to
fix
the
multiple. Hence, SL has a unique solution
x.
This shows
that
L is perfect.
Note
that
Proposition 16.5.1 still holds
if
we
replace the assumption: t
~
by
the
assumption: t
~
r2
and
t is the minimal norm of
L.
I
As
we
saw in
Lemma
13.2.11, every section
of
the contact polytope by a
hyperplane not containing
the
origin is a Delaunay polytope. Hence, Proposition
16.5.1
can
be reformulated as follows.
Proposition
16.5.2.
Let
L
be
a k-dimensionallattice with
minimal
norm t and
let P
be
a Delaunay polytope obtained by taking a section
of
the contact polytope
of
L
by
a hyperplane
not
containing the origin.
If
P is basic and extreme and
if
P contains two vertices
u,v
with (u v)2 =
t,
then L is perfect. I
For example, the root lattice Es
and
the
Leech lattice
A24
are perfect.
This
can
be
seen by applying Proposition 16.5.2; for E
s
, take t = 2
and
P =
321
whose squared radius is
~,
and
for
A24,
take t 32
and
P =
Pn
whose squared
radius is
24 (see Sections 16.2
and
16.3). Another example of perfect lattice is
the
lattice
Al6
n
{x
I x
T
a = 0
mod
(8)}, where A
16
is
the
Barnes-Wall lattice
and
a is a minimal vector of it; apply Proposition 16.5.2 with
the
polytope p
16
(see Section 16.4).
The
following result can also be checked.
Proposition
16.5.3.
Let P
be
an extreme basic Delaunay polytope with radius
r and let
V denote the lattice generated
by
the set
of
vertices
of
P and the center
of
P
(L'
is known
as
the centered lattice).
If
L'
has
minimal
norm
r2, then V
~~~t
I
For instance,
the
Schliifii polytope
221
is
an
extreme basic Delaunay polytope
in
E
6
•
The
lattice generated by
V(22d
and
its center is
the
dual lattice
E6
which
is indeed perfect.

M.M. Deza, M. Laurent, Geometry of Cuts and Metrics, Algorithms and Combinatorics 15,
DOI 10.1007/978-3-642-04295-9_17, © Springer-Verlag Berlin Heidelberg 2010
Chapter
17.
Hypermetric
Graphs
We
group
in
this
chapter
several results concerning
hypermetricity
of
distance
spaces arising from graphs.
There
are essentially two ways of
constructing
a distance space from a graph.
The
most
classical
construction
of a distance space from a connected
graph
G is
by
considering
the
graphic
metric
space
(V(
G),
de)
where
de
is
the
path
metric
of
G,
with
de
(u,
v)
denoting
the
smallest
length
of a
path
connecting
the
nodes
u,
v E V (G).
If
(V
(G),
de)
is
hypermetric
(resp. isometrically f I-embeddable,
of
negative
type),
we
say
that
G is a hypermetric graph (resp.
an
fl-graph, a graph
of
negative type).
Another
distance
space which
can
be
constructed
from a
graph
G is
the
space
(V(G),
de),
where
de
is
the
truncated distance
of
G defined by
ifij
E
E(G),i
#-j,
if
ij
~
E(G),
i
#-
j,
for all i E
V(G).
If
G
has
diameter
l
:::;
2,
then
these two notions
of
path
metric
and
truncated
distance
coincide.
This
is
the
case, for instance, for suspension graphs.
In
fact,
the
graphs
whose suspension is
of
negative
type
form a class
of
graphs
which
has
received a lot
of
attention
in
the
literature; indeed,
they
are
the
graphs
whose
adjacency
matrix
has
minimum
eigenvalue
greater
than
or
equal
to
-2.
For a
graph
G =
(V,
E)
on
n nodes
we
remind
that
its adjacency
matrix
Ae
is
the
n x n
symmetric
matrix
with
zero diagonal entries
and
whose
(i,j)-th
entry
is
equal
to
1
if
i, j
are
adjacent
in
G
and
to
0 otherwise, for
distinct
i, j E
V.
We
let
Amin(Ae)
denote
the
smallest eigenvalue
of
matrix
Ae.
We consider here questions
related
to
hypermetricity
and
fl-embeddability
for
either
of
the
two distances
de
and
de
attached
to
a
graph
G.
In
Sections
17.1
and
17.2
we
present a
number
of
results dealing
with
the
problem
of
char-
acterizing
the
graphs
whose
path
metric
or
truncated
distance
is
hypermetric
or
fl-embeddable.
We are interested, in
particular,
in
finding
'good'
character-
izations;
that
is, characterizations leading
to
polynomial
time
recognition algo-
rithms.
Such results are known for several classes of graphs. We focus
in
Section
17.1
on
suspension
graphs
and
on
bipartite
graphs
equipped
with
the
truncated
1
The
diameter
of
a
graph
G is defined
as
the
largest
distance
(with
respect
to
the
shortest
path
metric)
between
two
nodes
of
G.

252
Chapter
17.
Hypermetric
Graphs
distance. Section 17.2 deals
with
graphs
having some regularity properties. Fi-
nally, Section 17.3
studies
the
graphs
G for which
either
of
the
two
distances
dG
and
de
lies on
an
extreme
ray
of
the
hypermetric
cone.
17.1
Characterizing
Hypermetric
and
.e1-Graphs
Characterizing
Hypermetricity
and
CI-Embeddability
for
Path
Met-
rics.
We
start
with
a
characterization
of
the
graphs
whose
path
metric
is
hypermetric
or isometrically CI-embeddable, which follows directly from
The-
orems
14.3.6
and
14.3.7. (In fact,
the
characterization
of
CI-graphs will also
follow from
the
results
of
Shpectorov
[1993]
exposed in
Chapter
21.)
Theorem
17.1.1.
Let
G
be
a connected graph.
Then,
(i)
G is
hypermetric
if
and
only
if
G is an
isometric
subgraph
of
a
Cartesian
product
of
half-cube graphs, cocktail-party graphs
and
copies
of
the
Gosset
graph G
56
•
(ii) G is an C
I
-graph
if
and
only
if
G is an
isometric
subgraph
of
a
Cartesian
product
of
half-cube graphs
and
cocktail-party graphs. I
Several
characterizations
of
the
hypercube
embeddable
graphs
will
be
given
in
Chapter
19;
they
are good characterizations, in
the
sense
that
they
permit
to
recognize
whether
a
graph
is
an
isometric
subgraph
of
a
hypercube
in
polynomial
time.
The
result
from
Theorem
17.1.1 (ii) does not yield, a priori, a
good
char-
acterization
for CI-graphs. However,
the
proof
method
developed by
Shpectorov
[1993]
permits
to
recognize CI-graphs
in
polynomial
time
(see Corollary 21.1.9).
No
good
characterization
is known yet for
hypermetric
graphs
(recall
Remark
14.2.6).
We
state
this
as
an
open
problem.
Problem
17.1.2.
What
is the complexity
of
the problem
of
testing
whether
(the
path
metric
of)
a graph is
hypermetric
?
Problem
17.1.2 is solved for
the
class
of
suspension graphs. Indeed, for these
graphs,
some refined
characterizations
for
hypermetricity
and
CI-embeddability
are
known
that
lead, in
particular,
to
polynomial-time recognition
algorithms
(cf.
Theorems
17.1.8
and
17.1.9). A suspension
graph
has
diameter
S 2
and
thus
its
path
metric
coincides
with
its
truncated
distance.
The
graphs
whose
truncated
distance
is
hypermetric
or
CI-embeddable are not well
understood
in
general.
Good
characterizations
are, however, available for some subclasses;
for
instance,
for
bipartite
graphs
(cf.
Theorem
17.1.13)
and
for
graphs
with
regularity
properties
(cf. Section 17.2).
A
Good
Characterization
of
Hypermetricity
and
CI-Embeddability
for
Suspension
Graphs.
We consider here in
detail
suspension graphs. A first
observation
is
that,
for a
graph
G, its suspension
"VG
is
hypermetric
(resp.
an
C 1
-graph)
if
and
only
if
"V
H is
hypermetric
(resp.
an
C
I-graph)
for each
connected

17.1 A
Characterization
of
Hypermetric
and
il-Gr:!l.vtls
253
component
H
of
G. Indeed, the
path
metric
of
VG arises as the
I-sum
of
the
path
metrics
of
V
Hb
...
, V Hm, if
HI,
.
..
,Hm
are the connected components
of
G. (Recall Section 7.6.) Hence,
we
can
restrict
our
attention
to
the
case
when
G is a connected graph.
y
~
4!;b
B
=K
I
1.3
B2
B
3
-.:=
Ks - P 2
~
~
V
B4
B5 B
6=
K
6
- C 4
~
E1
*
B7
B8
B9=K6-
C
5
Figure 17.1.3:
The
excluded configurations for line graphs
We
start
with
a characterization
of
the suspension graphs
that
are
of
negative
type, which was
obtained
by Assouad
and
Delorme [1980]. (Compare
the
results
from
Propositions
17.1.4
and
17.2.1.)
Proposition
17.1.4.
Let
G
be
a graph. Then, its suspension VG is
of
negative
type
if
and only
if
Amin(AG)
;::
-2
holds.
Proof.
We
use
Proposition
13.1.2, so
we
show
that
Amin(AG)
;::
-2
if
and
only
if
the
space
(V(VG),
dVG)
has
a representation.
Let
io
denote
the
apex
node
of
VG
and
suppose
that
G has n nodes.
If
Amin(AG)
;::
-2,
then
the
matrix
Ac
+
2I
is positive semidefinite. Hence, there exist n vectors
UI,
...
,
Un
E
Jlll.m
(for some
m)
such
that
Then,
the
mapping
{
(u;)2
2
uTuj
1
uTuj
= 0
for i =
1,
...
, n,
if
ij
E E(G),
otherwise.
i
E
V(
G)
1-+
Ui,
io
1-+
Uo
0,
254
Chapter
17.
Hypermetric
Graphs
provides a
representation
of
(V(\7G),
2dvG). Indeed,
(Ui
-
Uj)2
= 2
if
ij
E
E(\7G)
and
(Ui
-
Uj)2
= 4 otherwise. All
the
above
arguments
can
be
reversed,
stating
the
converse implication:
If
\7G is
of
negative type,
then
Amin(AG)
:2:
-2.
I
We recall
that
L(H)
denotes
the
line
graph
of
a
graph
H.
It
is easy
to
see
that
the
suspension \7
L(H)
of
any line
graph
is
an
f\ -graph. Indeed,
if
we
label
the
apex
node
by
the
zero vector
and
each edge e
:=
ij
E
E(H)
by
the
vector
ei~ei
(ei
denoting
the
i-th
unit
vector
in
the
space ]W.V(H)),
then
we
obtain
an
£l-embedding
of
\7
L(H).
This
shows, moreover,
that
2d(\7
L(H))
is
hypercube
embeddable.
Line
graphs
have
been
characterized by Beineke
[1970]
by
means
of excluded
subgraphs.
Namely,
Theorem
11.1.5.
A graph G is a line graph
if
and
only
if
G does
not
contain
as
an
induced subgraph
any
of
the
nine
graphs
Bi
(1
::;
i
::;
9) shown
in
Figure
17.1.3. I
•
H4
Figure
17.1.6: Four
graphs
whose suspensions are
not
£l-graphs
Remark
11.1.1.
The
following
can
be
checked.
(i)
\7
Bi
is
not
an
£l-graph
for
aliI::;
i
::;
9 except i =
3;
in
fact, \7 B
l
,
B2 are
not
5-gonal
and
\7 B
4
,
\7
B6
are not 7-gonal.
(ii) For each
of
the
graphs Hi
(1
::;
i
::;
4)
shown
in
Figure 17.1.6, \7
Hi
is
not
an
£l-graph.

17.1
A Characterization of Hypermetric and
iI-Graphs
255
In
other
words, if d denotes the
path
metric of any of the graphs
V'
Bi
(1
:::;
i
:::;
9,i
f:.
3)
or
of
V'Hi
(1
:::;
i
:::;
4), there exists
an
inequality
vTx
:::;
0 defining a
facet of
CUT
7
which is violated by
d,
i.e., such
that
v
T
d >
O.
See Deza
and
Laurent [I992a] for
an
explicit description of such inequalities. I
Let G be a connected graph
and
suppose
that
its suspension V'G
is
hyper-
metric. Let
H denote
the
I-skeleton graph of
the
Delaunay polytope associated
with
the
space (V(V'G),2dvG). Then, V'G
is
an induced subgraph of
Hand
H
is one of the Delaunay polytope graphs shown in Figure 14.3.1. Therefore, if V' G
is
an
ii-graph
then, by Proposition 14.1.10, H
f:.
G27,
G
5
6
and, thus, H is one
of
J(m,
t),
tH(m,2)
and
K
mx
2. More precisely,
we
have the following results,
due to Assouad and Delorme [1980, 1982].
Theorem
17.1.8.
Let G
be
a connected graph. Then, the following assertions
are equivalent.
(i) V'G
is
an iI-graph.
(ii) G
does
not contain as an induced subgraph any
of
the graphs from the
family
(iii) G is a line graph
or
G is an induced subgraph
of
a cocktail-party graph.
Proof.
The
implication
(i)
=*
(ii) follows from the fact
that
the suspensions of
the graphs
from:F
are not iI-graphs.
The
implication (iii)
=*
(i) is clear.
We
now show
that
(ii)
=*
(iii) holds. Let G be a connected
graph
that
does not
contain any member of
:F
as
an
induced subgraph.
If
G does not contain
B3
as
an
induced subgraph,
then
G is a line
graph
by Theorem 17.1.5. Hence,
we
can
suppose
that
B3
is an induced subgraph of G; say,
B3
= G[Y] is
the
subgraph
of
G induced by
the
subset of nodes
Y,
WI
=
5.
We
show
that
G is
an
induced
subgraph
of a cocktail-party graph. For this consider the following property (P):
(P)
For each subset Z
~
V(G)
such
that
Y
~
Z and for each i E
V(G)
\
Z,
if
G[Z]
is
an
induced subgraph of a cocktail-party graph
and
if
G[Z
U
{ill
is
connected,
then
G[Z
U {i}] is also an induced subgraph of a cocktail-party
graph.
We
show
that
(P)
holds by induction on
IZI.
Case
1.
We
show
that
(P) holds for Z
::::
Y.
Let i E
V(G)
\ Y such
that
the
graph
G[Y
U
{ill
is connected. So,
G[YU
{ill
is a connected graph on six nodes
containing Ba
=
K5
\
Pz
as an induced subgraph.
By
direct inspection, one can
check
that
there are eleven connected graphs on six nodes containing
B3
as an
induced subgraph. Among them,
we
find H
lo
H
2
,
H3,
H4i
we
also find two graphs
containing
B2
and
three graphs containing B
l
;
these cases are excluded since G

256
Chapter
17.
Hypermetric
Graphs
does
not
contain
any
member
of
:F.
The
remaining
two
graphs
are
K6
\
P2
and
\7\7 K
2X2
which
are, respectively,
induced
subgraphs
of
K
5X2
and
K
4x
2.
Hence,
the
property
(P)
holds
for Z =
Y.
Consider
now Z
such
that
Y
~
Z
~
V(G),
IZI
~
6
and
G[Z]
is
an
induced
subgraph
of
a
cocktail-party
graph,
and
let
i E
V(G)
\ Z
such
that
G[Z U
{ill
is
connected.
Set
Y
:=
{Yl,Y2,Y3,Y4,Y5} where, for
instance,
Yl
and
Y2
are
not
adjacent
in
G
and,
thus,
every
other
pair
of
nodes
of
Y is
adjacent
in
G.
Case
2.
Let
s,
t E Z
such
that
sand
t
are
not
adjacent
in
G. We show
that
i
is
adjacent
to
both
sand
t.
Since
G[Z]
is
contained
in
a
cocktail-party
graph,
every
other
node
of
Z is
adjacent
to
both
sand
t.
Let
u E Z
be
a
node
which
is
adjacent
to
i.
Then,
i is
adjacent
to
at
least one
of
s
or
t (else,
G[{u,s,t,i}]
would
be
a
induced
subgraph
Bl
of
G). Hence, for
U:=
{S,t,Y3,Y4,Y5},
G[U]
is
B3
and
G[U U
{ill
is
connected.
By
Case 1, we
deduce
that
G[U U
{ill
is
an
induced
subgraph
of
a
cocktail-party
graph,
which
implies
that
i is
adjacent
to
both
sand
t.
Case
3.
Let
s, t E Z
such
that
sand
t
are
adjacent
in
G. We show
that
i is
adjacent
to
at
least
one
of
s
or
t.
If
there
exists r E Z
which
is
not
adjacent
to
s
then,
by
Case
2,
i is
adjacent
to
both
rand
s. Similarly,
if
there
exists r E Z
which
is
not
adjacent
to
t,
then
i is
adjacent
to
t. Else,
each
r E Z is
adjacent
to
both
sand
t.
Let
r E Z
which
is
adjacent
to
i. We
can
find a set U
such
that
lUI
=
5,
r, s, t E U
and
G[U]
= B
3
. Therefore,
G[U
U
{ill
is
an
induced
subgraph
of
a
cocktail-party
graph,
which
implies
that
i is
adjacent
to
at
least
one
of
s
or
t.
We
deduce
from
Cases
2
and
3
that
G[Z U
{ill
is
an
induced
subgraph
of
a
cocktail-party
graph.
So, we have
shown
that
(P)
holds. I
Theorem
17.1.9.
Let
G
be
a connected graph.
The
following
assertions
are
equivalent.
(i)
\7G
is a
hypermetric
graph, but
not
an f\ -graph.
(ii) G is
an
induced subgraph
of
the Schliifli graph
G27
and
G
contains
as an
induced
subgraph one
of
the graphs
of
the
family
Proof. (i)
~
(ii)
By
Theorem
17.1.8,
if\7G
is
not
an
£l-graph,
then
G
contains
as
an
induced
subgraph
one
of
the
members
of
:F
and,
in
fact,
of
:Fa
since \7 B
1
,
\7B2, \7B4' \7B6
are
not
hypermetric
(recall
Remark
17.1.7).
Let
P
denote
the
Delaunay
polytope
associated
with
the
hypermetric
space (V(\7G),2d'Vc)
and
let H
denote
its
I-skeleton
graph.
By
Proposition
14.3.5, P is a
generating
Delaunay
polytope
in
a
root
lattice.
Thus,
P is a
direct
product
of
Delaunay
polytopes
from
Figure
14.3.1
and
H is a
direct
product
of
Delaunay
polytopes
graphs
from
Figure
14.3.1.
In
fact, since
the
graph
G is
connected,
H is
not
a
direct
product,
i.e., H is one
of
the
Delaunay
polytope
graphs
from
Figure

17.1 A
Characterization
of
Hypermetric
and
{iI-Graphs
257
14.3.1. Now, H is G
2
7
or G
56
since all
the
other
Delaunay
polytope
graphs
are
{iI-graphs. Therefore,
VG
is
an
isometric
subgraph
of G
56
and,
thus,
G is
an
isometric
subgraph
of
G27.
The
implication
(ii)
~
(i) is clear. I
Corollary
17.1.10.
Let
G
be
a connected graph
on
n nodes.
(i)
If
n
2:
37,
then
VG
is an {iI-graph
if
and
only
if
VG
is 5-gonal
and
of
negative type.
(ii)
If
n
2:
28,
then
VG
is an {iI-graph
if
and
only
ifVG
is hypermetric. I
A
Good
Characterization
of
Hypermetricity
and
{i1-Embeddability
for
Truncated
Distances
of
Bipartite
Graphs.
We consider now,
more
gener-
ally, {i1-embeddability
and
hypermetricity
for
truncated
distances of graphs. For
bipartite
graphs, Assouad
and
Delorme [1982] have
obtained
several equivalent
characterizations,
leading
to
a
polynomial-time
recognition algorithm;
they
are
formulated
in
Theorem
17.1.13 below.
n+l
•
I
• •
I
•
2 3 4
n-2
n-l
n
IS
n
6
• •
I
• • • •
•
1 2 3
4 5 7 8 9
E8
6
7
I
6
•
• •
•
•
•
8
1 2
3
4 5 7
2
3
4 5
E7 E6
Figure
17.1.11:
2 - - - -
The
graphs
D
n
,
Es,
E7,
E6
2The
graphs
15",
Ea,
E
7
,
E6
and
An
:=
0,,+1 arise,
in
fact, as
the
Dynkin
diagrams
of
the
root
lattices
(cf.
Brouwer,
Cohen
and
Neumaier
[1989]).
