Deza M.M., Laurent M. Geometry of Cuts and Metrics
Подождите немного. Документ загружается.


28D
Chapter
18. Preliminaries on
Graphs
Given two
graphs
G
and
H,
their Cartesian product is
the
graph
G x H
with
node
set
V(G)
x
V(H)
and
whose edges are
the
pairs
«a,x),
(b,y» with a,b E V(G),
x,y
E
V(H)
and,
either
(a,
b)
E
E(G)
and
x y,
or
a =
band
(x,y)
E
E(H).
The
Cartesian
product
HI x
...
X
Hie
of
k
graphs
HI,
...
,
Hie
is
also
denoted
Ie
as
II
H
h
· A Hamming
graph
is a
Cartesian
product
of
complete graphs, i.e.,
h=l
m
of
the
form
II
K
qj
for some integers qI,
...
, qm, m
;::::
1. Note
that
the
graphic
j=1
m
metric
space
of
the
Hamming
graph
II
K
qj
coincides with
the
Hamming
distance
j=1
m
space
(II
{D,
1,
...
,qj
- I}, d
H
).
The
m-hypercube
graph
is
the
graph
H(m,2)
j=1
with
node set {D,l}m
and
whose edges are the pairs
(x,y)
E {D,l}m x {D,l}m
with
dH(x, y) =
1;
H(m,
2)
has 2
m
nodes
and
m2
m
-
1
edges. Hence,
H(m,2)
is
isomorphic
to
the
Hamming
graph
(K2)m
and
its graphic metric space coincides
with
the
space
({D,
l}m, dH)' Equivalently, given a finite set
n,
the
Inl-hypercube
graph,
also
denoted
as
H(n),
can
be defined as
the
graph
whose node set is the
set
of
all subsets
of
n
and
whose edges are
the
pairs
B)
of
subsets
of
n such
that
IA
. .6BI =
1.
The
half-cube graph
~H(m,
2) is
the
graph
whose node set is
the set of all subsets of even cardinality
of
{I,
...
) m}
and
with
edges
the
pairs
(A,
B)
such
that
IA.6BI =
2.
The
cocktail-party graph Kmx2 is
the
complete
multipartite
graph
with
m
parts,
each
of
size
2.
Hence, Krnx2 is
the
graph
on
2m
nodes
VI,
.•.
) V2m whose edges are all
pairs
of
nodes except
the
m
pairs
(Vi,
Vi+m)
for i = 1,
...
,
m.
A connected
graph
G is said
to
be
hypercube embeddable
if
its
nodes
can
be
labeled
by
binary
vectors in such a way
that
the
distance between two nodes
coincides with
the
Hamming
distance between
their
labels (or, equivalently, if its
path
metric
dG
can
be
decomposed as a nonnegative integer combination
of
cut
semimetrics).
In
other
words, G is hypercube embeddable
if
G is
an
isometric
subgraph
of
(K2)m for some m
;::::
1.
Then,
the
smallest integer m such
that
G
can
be isometrically
embedded
into
H(m,2)
is
denoted
by
mh(G). Note
that
mh(G)
coincides with
the
notion of
minimum
h-size sh(dG) for the
path
metric
of
G (introduced
in
Section 4.3).
The
graph
G is said
to
be
an
i
l
-graph if its
path
metric
dG
is
ii-embeddable.
Equivalently, by Proposition 4.3.8, G is
an
ii-graph
if
G
is
hypercube embeddable,
up
to
scale;
then
the smallest integer
T/
such
that
1}dG
is hypercube embeddable is called
the
minimum
scale
of G.
Gis
an
ii-rigid graph
if
its
path
metric
dG
is
ii-rigid
(see Section 4.3 for
the
definition
of
ii-rigidity).
Observe
that
the
Cartesian
product
G x H is
an
ii-rigid
graph
if
and
only if
both
graphs G
and
H are
ii-rigid
(see Section 7.5).
More generally, a
graph
G is
an
isometric
subgraph
of a
Hamming
graph
if
and
only if its
path
metric
dG
can be decomposed as a nonnegative integer
combination of
multicut
semimetrics (recall Proposition 4.2.9).
If
(SI,
...
, St) is
a
partition
of
V
n
,
then
the
multicut
semimetric
8(SI,""
St)
can
be
decomposed

Chapter
18. Preliminaries on Graphs
281
in
the
following way:
1
2
E
O(Si).
i$i<;t
This
implies
that,
for every isometric subgraph G of a
Hamming
graph, 2da
is a nonnegative integer combination of
cut
semimetrics, i.e., 2da
is
hypercube
embeddable.
In
other
words, every isometric
subgraph
of a
Hamming
graph
is
an
ii-graph
with
scale
:s;
2 or, equivalently,
is
an
isometric
subgraph
of a half-cube
graph.
We
summarize in
the
figure below
the
links existing between
the
various
embeddings
just
discussed.
In
fact, as
we
will see here, each of
the
following
graph
properties
can
be
checked in polynomial time.
G is hypercube embeddable
G is
an
isometric subgraph of a Hamming
graph
G is
an
isometric
subgraph
of a half-cube
graph
~
G is
an
ii-graph

M.M. Deza, M. Laurent, Geometry of Cuts and Metrics, Algorithms and Combinatorics 15,
DOI 10.1007/978-3-642-04295-9_19, © Springer-Verlag Berlin Heidelberg 2010
Chapter
19.
Isometric
Embeddings
of
Graphs
into
Hypercubes
We
study
in
this
chapter
the
graphs
that
can
be
isometrically
embedded
into
hypercubes. We give several equivalent characterizations for these
graphs
in
Theorems
19.1.1, 19.2.1, 19.2.5
and
19.2.8. As
an
application, one
can
recog-
nize
in
polynomial
time
whether
a
graph
can
be
isometrically
embedded
in
a
hypercube.
Hypercube
embeddable
graphs
admit,
in
fact,
an
essentially unique
embedding
in a hypercube; two formulations for
the
dimension
of
this
hypercube
are given in
Propositions
19.1.2
and
19.2.12.
19.1
Djokovic's
Characterization
We recall
that,
given a
graph
G =
(V,
E), a
subset
U
<;;;
V
is
said
to
be
da-convex
or, simply, convex if it is closed
under
taking
shortest
paths.
We now
state
the
main
result
of
this
section, which is a
structural
character-
ization
of
the
hypercube
embeddable
graphs,
due
to
Djokovic [1973]. Recall
the
definition
of
the
set
G(a,
b)
from relation (18.0.1).
Theorem
19.1.1.
Let
G
be
a connected graph. The following assertions are
equivalent.
(i) G can
be
isometrically embedded
into
a hypercube.
(ii) G is bipartite
and
G(
a,
b)
is convex
for
each edge (a,
b)
of
G.
Proof. (i)
~
(ii)
If
G
is
hypercube embeddable,
then
its
path
metric
da
satisfies
da(a,
b)
+
da(a,
c)
+ da(b,
c)
==
0
(mod
2)
for all
nodes
a,
b,
c
of
G,
which means
that
G
is
bipartite.
Let us now check
the
convexity
of
G(a,
b)
for all adjacent nodes a,
b.
Let (a,
b)
be
an
edge
of
G,
let
x,
y E G (a,
b)
and
z E V lying
on
a
shortest
path
from x
to
y.
Consider a
hypercube
embedding
of
G
in
which node a is labeled by
0,
node b
ii'
labeled
by
a singleton
{I},
and
nodes x,
y,
z are labeled by
the
sets
X,
Y,
Z.
Then,
1
rt
X,Y
since
X,y
E
G(a,
b),
and
IX.0:.YI = IX.0:.ZI +
IY.0:.ZI
since
da(x,y)
=
da(x,
z)
+
da(z,
y).
This
implies
that
1
rt
Z,
i.e.,
that
z E
G(a,
b).
This
shows
that
the
set
G(
a,
b)
is
convex.
(ii)
~
(i) We first show
that,
given two edges e = (a,
b),
e' = (a',
b')
of
G, e()e' if
and
only
if
the
two
bipartitions
of V into
G(a,
b)
UG(b, a)
and
G(a',
b')
UG(b',
a')

284
Chapter
19. Isometric
Embeddings
of
Graphs
into
Hypercubes
are identical. Suppose, for instance,
that
a' E G(a,
b)
and
b'
E G(b, a).
We
show
that
G(a,
b)
= G(a', b'). For this,
it
suffices
to
check
that
G(a,
b)
<::::
G(a', b'). Let
x E G(a,b).
If
x E G(b', a'),
then
b'
lies
on
a
shortest
path
from x
to
a'. By
the
convexity of G(a,
b),
this
implies
that
b'
E G(a,
b),
yielding a contradiction.
Therefore,
the
relation
B
is
transitive. Let E
:=
E / B denote
the
set of equivalence
classes
of
the
relation
B.
For e E E, let e denote
the
equivalence class of e
in
E.
SO,
all edges
(a,
b)
of a
common
equivalence class correspond
to
the
same
bipartition
G(a,
b)
U G(b,
a)
of
V.
Fix
a node
Xo
of G. For each node x E
V,
let
A(x)
denote
the
set
of
all e E E for which x
and
Xo
belong to
distinct
sets
of
the
bipartition
V = G(a,
b)
U G(b, a), if
(a,
b)
is
an
edge of
e.
In
particular,
A(xo) =
0.
We show
that
this
labeling provides a hypercube
embedding
of
G,
i.e.,
that
IA(x)6A(y)1 = dG(x,y)
holds for all nodes x, y E
V.
Let x, y E V
and
m
:=
dG(x, y). Let P
:=
(xo
=
x,
Xl,
...
,x
m
= y) be a
shortest
path
in G from x
to
y,
with
edges
ei
= (Xi-I,
Xi)
for i = 1,
...
,
m.
We claim
that
A(x)6A(y)
=
{el,""
em}.
Clearly, each
ei
belongs to
A(x)6A(y).
Indeed if, for instance,
Xo
E
G(Xi-l,Xi),
then
ei
E
A(y)
\
A(x)
since x E G(Xi-J,Xi)
and
y E
G(Xi,Xi-l).
Conversely, let
e =
(a,
b)
E E such
that
e E
A(x)6A(y).
We
can suppose, for instance,
that
e E
A(y)
\
A(x)
with
xo, x E G(a,
b)
and
y E G(b, a). Let i be the largest index
from
{I,
...
,p} for which
Xi-l
E G(a,
b).
Then,
eiBe,
which shows
that
e =
e;.
Therefore,
we
have shown
that
IA(x)6A(y)1 = da(x,
y)
holds for all nodes x, y E
V.
This
shows
that
G can
be
isometrically
embedded
into
the
hypercube
of
dimension
dimJ(G)
:=
lEI.
I
The
following result from Deza
and
Laurent
[1994a] will also be a consequence
of
Theorem
20.3.1.
Proposition
19.1.2.
If
G is hypercube embeddable, then G is f1-rigid; in par-
ticular,
G has a unique (up to equivalence) isometric embedding into a hypercube
whose dimension
is
mh(G)
=
dimJ(G).
Proof. Suppose
that
G is
hypercube
embeddable.
We
show
that
Gis
f1-rigid.
Then,
this
will
imply
that
G has a unique hypercube embedding
and,
therefore,
that
mh(G)
=
dimJ(G).
We keep the
notation
from
the
proof
of
Theorem
19.1.1.
For
each e E E
with
e =
(a,
b),
let 8
e
denote
the
one
of
the two sets G(a,
b)
and
G
(b,
a)
that
does
not
contain
the
fixed node
Xo.
From
the fact
that
dG
(x, y) =
IA(x)6A(y)1
for all nodes X,y E
V,
we
deduce
that
dG
can
be decomposed as
dG
=
2..=
0(8
e
).
eEE
Let
F G
denote
the
smallest face
of
the
cut
cone
CUT
n (n
is
the
number
of
nodes
of
G)
that
contains
dG.
We claim
that
FG
is a simplex face
of
CUTn
of
dimension
19.1 Djokovic's
Characterization
285
dim[(G).
Clearly, all
the
cut
semimetrics
O(Se:)
(e
E
E)
belong
to
Fe
and
they
are
linearly independent. We show
that
every
cut
semimetric
O(S)
lying
on
Fe
is
of
the
form
O(Se:)
for some e E
E.
If
this
is
the
case,
then
we
have indeed shown
that
Fe is a simplex face
ofCUT
n
of
dimension
lEI
=
dim[(G).
Let S be a
subset
of
V such
that
O(S)
E Fe.
Then,
O(S)
satisfies
the
same
triangle equalities as
de. As
the
graph
G
is
connected,
we
can
find
an
edge e = (a,
b)
such
that
a E S
and
b E V \
S.
Suppose, for instance,
that
Xo
E
G(b,
a),
i.e.,
Se:
= G(a,
b).
As
de satisfies
the
triangle
equality de(xo,
a)
= de(xo,
b)
+de(a,
b),
we
deduce
that
O(S)
satisfies
the
equality o(S)(xo,
a)
= o(S)(xo,
b)
+ o(S)(a,
b),
which implies
that
Xo
E
V\S.
We claim
that
S = G(a,
b)
holds.
If
x E G(a,
b),
then
dc(x,
b)
=
de(x,
a)+de(a,
b)
from which
we
deduce
that
o(S)(x,
b)
= o(S)(x, a)+o(S)(a,
b),
implying
that
xES.
In
the
same
way,
G(b,
a)
is contained in
V\S,
which implies
that
S = G(a,
b).
I
Xo
11000000
0000000
el
ez
1000000
e6
10000100
e8
f7J
10110000
10101000
10000101
10000110
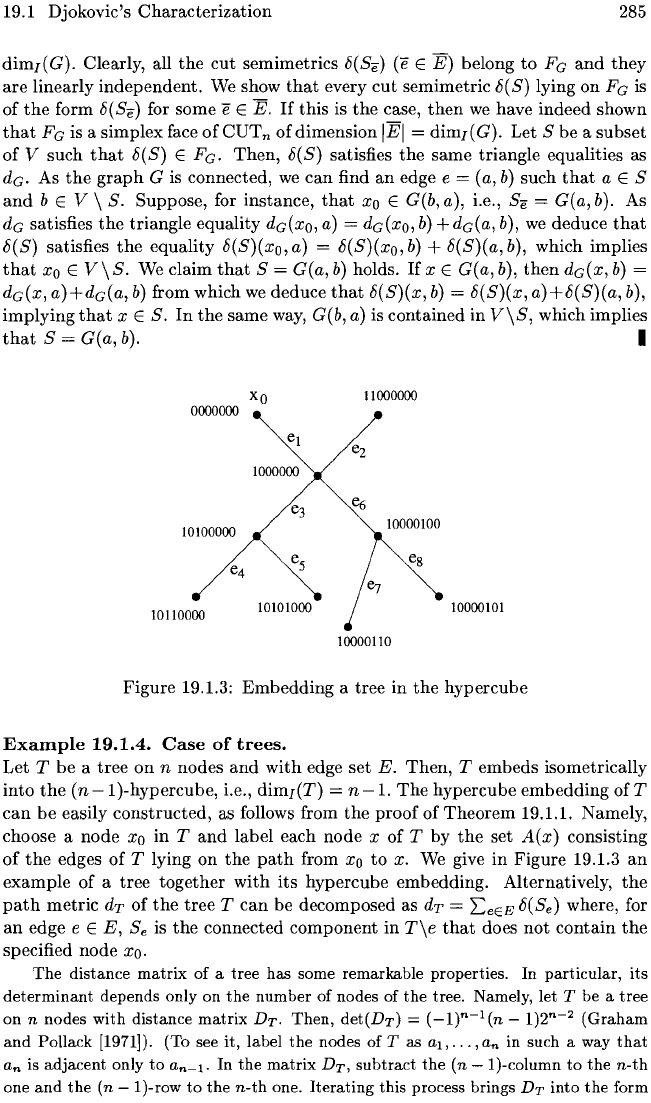
Figure
19.1.3:
Embedding
a
tree
in
the
hypercube
Example
19.1.4.
Case
of
trees.
Let
T
be
a
tree
on
n nodes
and
with
edge
set
E.
Then,
T embeds isometrically
into
the
(n
-I)-hypercube,
i.e.,
dim[(T)
= n
-1.
The
hypercube
embedding
of T
can
be
easily
constructed,
as follows from the
proof
of
Theorem
19.1.1. Namely,
choose a node
Xo
in
T
and
label each node x of T by
the
set
A(x)
consisting
of
the
edges
of
T lying
on
the
path
from
Xo
to
x. We give
in
Figure
19.1.3
an
example
of a
tree
together
with
its
hypercube embedding. Alternatively,
the
path
metric
d
T
of
the
tree
T
can
be decomposed as d
T
=
LeEE
o(Se)
where, for
an
edge e E
E,
Se is
the
connected
component
in
T\e
that
does
not
contain
the
specified node
Xo.
The
distance
matrix
of
a
tree
has
some remarkable properties.
In
particular,
its
determinant
depends
only
on
the
number
of
nodes of
the
tree. Namely, let T
be
a
tree
on
n
nodes
with
distance
matrix
DT.
Then,
det(DT)
=
(_I)n-l
(n - 1)2
n
-
2
(Graham
and
Pollack
[1971]).
(To see
it,
label
the
nodes
of
T
as
al,
.
..
, an in such a way
that
an is
adjacent
only
to
an-I.
In
the
matrix
D
T
,
subtract
the
(n -
I)-column
to
the
n-th
one
and
the
(n -
I)-row
to
the
n-th
one.
Iterating
this
process brings
DT
into
the
form

286
Chapter
19. Isometric
Embeddings
of
Graphs
into Hypercubes
of an n x n symmetric matrix having all entries equal to 0 except the (1,
i)-
and
(i,l)
entries equal to 1 and the (i, i)-entries equal to -2,
for
i = 2,
...
, n.) Graham and Lovasz
[1978J
show, more generally,
how
the coefficients of the characteristic polynomial of DT
can be expressed
in
terms of the number of occurrences of certain forests
in
T.
I
Remark
19.1.5.
As
an
immediate
consequence
of
Theorem
19.1.1, one
can
test
in
polynomial
time
whether
a
graph
G
is
hypercube embeddable. Moreover,
the
minimum
dimension
mh(G)
of
a
hypercube
containing G as
an
isometric
subgraph
can
also
be
computed
in
polynomial time, since
it
coincides
with
the
isometric dimension
dimr(G)
of
G (by
Proposition
19.1.2).
Suppose G is a
graph
on n nodes
with
m edges.
Aurenhammer
and
Hagauer
[1991]
present
an
algorithm
for
testing
whether
G is
hypercube
embeddable
that
runs
in
time
O(n
2
Iogn)
using
O(n
2
)
space.
Their
algorithm
is based
on
the
char-
acterization
from Corollary 20.1.3 (iv);
that
is, it consists
of
checking
whether
G is
bipartite
and
whether
the
relation
()
is transitive. Feder
[1992]
proposes
another
algorithm
running
in
time
O(mn)
and
using O(m) space;
its
space com-
plexity is
better
than
in
the
previous algorithm as one
can
easily check
that
m ::;
~n
log2
n if G is hypercube embeddable. Feder's
algorithm
is based
on
the
results
of
Section 20.1;
that
is,
it
consists
of
checking
whether
all
the
factors
in
the
canonical
metric
representation
of
G are isomorphic to K
2
•
I
19.2
Further
Characterizations
We
start
with
presenting two
further
characterizations for
hypercube
embeddable
graphs,
due
respectively to Avis
[1981]
and
to
Roth
and
Winkler [1986].
Theorem
19.2.1.
Let
G
be
a connected graph. Then, G is hypercube embeddable
if
and
only
if
G is bipartite
and
da
satisfies the following 5-gonal inequality:
(19.2.2)
d(i
l
,i
2
)+d(i
l
,i3)+d(i2,i3)+d(i4,i5)-
L
d(ih,ik)::;O
for
all nodes
il,'"
,i5 E
V.
h=1,2,3
k=4,5
Proof.
If
G
is
hypercube
embeddable,
then
its
path
metric
da
is
ll-embeddable
and,
therefore, satisfies
the
5-gonal inequality by
Theorem
6.3.1. Suppose now
that
G is
bipartite
and
not
hypercube embeddable.
Then,
by
Theorem
19.1.1,
there
exists
an
edge (a,b)
ofG
for which
the
set
G(a,b)
is
not
convex. Hence,
there
exist
x,
y E
G(a,
b)
and
z E G(b, a) such
that
da(x,
z)
+da(z,
y)
=
da(x,
y).
Consider
the
inequality (19.2.2) for
the
nodes
il
=
X,
i2
= y,
i3
=
b,
i4
=
a,
and
i5
= z.
One
computes
easily
that
the
left
hand
side
of
(19.2.2) takes
the
value
2, which shows
that
d
a
violates some 5-gonal inequality. I

19.2
Further
Characterizations
287
x y a b s
x
0 1
n+l
n 1
y 1
0
n
n+l
2
a
n+l
n 0 1
n
b n
n+l
1 0
n+l
s
1 2
n
n+l
0
Figure
19.2.3:
The
distance space
A(n)
on
the
5
points
of
{x,
y, a,
b,
s}
x y a b r
s
x
0 1
m+l
m p
p+l
y 1 0 m
m+l
p+l
p+2
a
m+l
m
0 1
n+l
n
b m
m+
1
1
0 n
n+l
r p
p+l
n+l
n 0
1
s
p+l
p+2
n
n+l
1 0
Figure
19.2.4:
The
distance space
B(m,
n,p)
on
the
6
points
of
{x, y,
a,
b,
r,
s}
Theorem
19.2.5.
Let
G
be
a connected bipartite graph. Then, G is hypercube
embeddable
if
and only
if
the space
(V,
de)
does
not
contain
as
an isometric sub-
space any
of
the spaces
A(n)
or
B(m,n,p),
whose distance matrices are shown
in
Figures 19.2.3 and 19.2.4, respectively.
Proof.
Suppose
that
G
is
not
hypercube
embeddable.
Then,
by
Theorem
19.1.1,
there
exists
an
edge
(a,
b)
of
G for which G(
a,
b)
is
not
closed. Let P be
an
isomet-
ric
path
in
G connecting two nodes of G(a,
b)
such
that
P
meets
G(b,
a)
and
P
has
minimal
length
with
respect to these properties. Say, P = (y,
x,
Zl,
...
,
Zk,
r,
s),
where
v,s
E G(a,b)
and
x,r
E G(b,a).
Set
m =
de(x,b),
n =
de(r,b)
and
p =
de
(x, r) (hence, p = k + 1).
One
can
check
that
the
distances between
the
points
a,
b,
x, y, r, s are entirely
determined
by
the
parameters
m,
n, p. Namely,
if
both
points
x
and
r coincide,
then
p =
0,
m =
n,
and
the
5-point subspace
({x,
y, a,
b,
s},
de)
of
(V,
de)
coincides
with
the
space
A(n),
whose distance ma-
trix
is shown in
Figure
19.2.3.
If
the
points
x
and
r are distinct,
then
the
6-point
subspace
({x, y,
a,
b,
r,
s},
de)
coincides
with
the
space
B(m,
n,p),
whose distance
matrix
is shown
in
Figure
19.2.4.
Conversely, if
(V,
de)
contains
A(n)
or
B(m,n,p)
as
an
isometric subspace,
then
G is
not
hypercube
embeddable, by
Theorem
19.2.1. Indeed,
both
A(n)
and
B(m,n,p)
violate
the
5-gonal inequality; namely,
they
violate
the
inequal-
ity
(19.2.2) for
{il,i2,i3}
=
{b,y,s}
and
{i4,i5} =
{x,a}.
I
Recall
that,
for a finite distance space (X,
d),
the
following chain
of
implica-
tions
holds (see
Proposition
4.3.8,
Theorems
6.2.16
and
6.3.1).

288
Chapter
19. Isometric Embeddings of
Graphs
into Hypercubes
(X,
d)
is
hypercube
embeddable
==>
(X,
d)
is
i\
-embeddable
==>
(X,
d)
is
hypermetric
==>
(X,
d)
is
of
negative
type
==>
the
distance
matrix
of (X,
d)
has exactly one positive eigenvalue.
Figure 19.2.6:
The
metric hierarchy
In
addition,
We recall (from
Lemma
6.1.14
and
Theorem
6.2.2)
the
following
equivalences.
(X,
d)
is
of
negative
type
~
(X,
Vd)
is
1:
2
-embeddable
the
matrix
(d(x,
xo)
+ d(y,
xo)
- d(x,
y)
)x,YEX\{xo}
is
positive
semidefinite, where
Xo
is a given element
of
X.
Figure
19.2.7: Characterizing
1:
2
-embeddability
Roth
and
Winkler
[1986]
show
that,
for
the
graphic metric spaces of
bipartite
graphs,
the
metric hierarchy from Figure 19.2.6 collapses. (Blake
and
Gilchrist
[1973]
had
earlier observed
that
connected
bipartite1:
1
-graphs are
hypercube
embeddable.)
Theorem
19.2.S.
Let
G
be
a connected bipartite graph. The following assertions
are equivalent.
(i)
G is hypercube embeddable.
(ii) G is an
1:1
-graph.
(iii) G is hypermetric.
(iv) G is
of
negative type.
(v) The distance
matrix
of
G has exactly one positive eigenvalue.
Proof.
It
suffices
to
show
that,
if G
is
not
hypercube embeddable,
then
its
dis-
tance
matrix
DG has
at
least two positive eigenvalues. Suppose
that
G
is
not
hypercube
embedable.
By
Theorem
19.2.5,
(V,
dG)
contains as
an
isometric sub-
space a space
C which is one
of
the
forbidden subspaces
A(n)
or
B(m,
n,p).
In
other
words,
the
distance
matrix
Dc
of C
is
a principal
submatrix
of DG.
Clearly,
Dc
has
at
least one positive eigenvalue since
its
trace is equal
to
O.
If
we
can
show
that
Dc
has
at
least two positive eigenvalues
then,
by applying
Lemma
2.4.4,
we
deduce
that
the
number
of positive eigenvalues of
DG
is
greater
than
or
equal
to
the
number
of
positive eigenvalues of
Dc
and, therefore,
that
DG has
at
least two positive eigenvalues.
Consider first
the
case
when
C is
of
the
form
A(n).
One
can
check
that
the
determinant
of
Dc
is
equal to
-8n(n
+ 1). Hence,
Dc
is
nonsingular
and
has
at
least two positive eigenvalues (indeed, if
Dc
would have only one positive
eigenvalue,
then
its
determinant
would
be
positive).

19.2
Further
Characterizations
289
Suppose now
that
Cis
of
the
form
B(m,n,p).
One
can
check
that
the
determi-
nant
of
Dc
is equal to
4(
4mnp + 2mp + 2np +
2mn
- m
2
_
n
2
_
p2),
which
can
be
rewritten
as
16mnp+4(n+p-m)(p+m-n)+4(p+m-n)(m+n-p)+4(m+n-p)(n+p-m).
As
m,
n,
p
are
the
distances between pairs
of
nodes
of
G,
we
deduce from
the
triangle
inequality
that
each
of
the
quantities into parentheses in
the
above ex-
pression
is
nonnegative. Hence,
the
determinant
of
Dc
is
positive.
This
implies
that
Dc
is nonsingular
and
has
at
least two positive eigenvalues (else, its deter-
minant
would be negative). I
Remark
19.2.9.
All
the
implications in
the
metric hierarchy from Figure 19.2.6
are
strict
for general (nonbipartite) graphs.
We
present here a unified set
of
counterexamples for
the
converse implications, proposed by A vis
and
Maehara
[1994], which is based on
the
graph
Kn
\P
3
(with
P
a
denoting
the
path
on
3
nodes).
This
remark
is, therefore, a continuation
of
Example
14.4.9.
The
metric
d(Kn
\P
3
)
was considered in Example 14.4.9 for disproving some implications
between
the
properties
of
being hypermetric
or
of
negative
type
or of
having a
spherical representation.
The
treatment
there was based
on
features
of
Delaunay
polytopes, while we use here conditions involving linear inequalities.
•
The
path
metrics
of
K4\P
3
,
K
5
\P
3
,
and
K6\P
3
are
iI-embeddable
(since 2dc
is
hypercube
embeddable),
but
not
hypercube embeddable (since they contain
three
points
at
pairwise distances one).
•
The
path
metrics
of
K
7
\P
3
,
K8\P
3
are
hypermetric,
but
not
iI-embeddable.
(Hint:
The
inequality:
Xij
:::;
0
)=4,5,6,7
j=4,5,6,7
is valid for
the
cut
cone
CUT
7 (this
is
the clique-web inequality:
CW?(3,
2, 2,
-1, -1,
-1,
_l)T
x:::;
0
which defines a facet of
CUT
7
;
see
Chapter
29).
But,
the
path
metric
of
K
7
\P3
violates
this
inequality if P
3
is
the
path
(2,1,3)
in
the complete
graph
K7 on
the
nodes 1,2,3,4,5,6,7. Hence, K
7
\P
3
is
not
an i!l-graph.)
•
The
path
metrics
of
Kg
\P3,
KlO
\P
3
are of negative type,
but
not
hypermetric.
(Hint:
The
path
metric
of
Kg
\P3 violates
the
hyperrnetric inequality:
-1,
-1, -1,
_l)T
x:::;
0
if
P3
is
the
path
(2,1,3).
To see
that
the
path
metric
of
KlO
\P3 is
of
negative
type,
one
can
use
Theorem
6.2.16. Namely,
it
suffices
to
check
that
the
bordered

290
Chapter
19.
Isometric
Embeddings
of
Graphs
into
Hypercubes
matrix
M =
(~
~)
has
exactly
one positive eigenvalue, where D
denotes
the
distance
matrix
of
KlO \P3.
One
can
indeed
check
that
the
eigenvalues
of
Mare
4 + y41, 0, 4 -
y41
and
-1
(with
multiplicity
8). )
•
The
distance
matrix
of
Kll
\P
3
has
exactly
one positive eigenvalue,
but
Kn
\P3
is
not
of
negative
type;
the
distance
matrix
of
Kn
\P
3
has
two
positive
eigenvalues
for all
n
::::
12. (Hint:
Kll
\P
3
is
not
of
negative
type
since
it
violates
the
negative
type
inequality:
(
24 16 16
)T
Qll
- - -
-1 -1 -1 -1
-1
-1
-1
-1
x < 0
7' 7'
7'
, , , , , " -
if
P
3
is
the
path
(2,1,3).)
Another
example
of
a
graph
which is
not
of
negative
type
but
whose
distance
matrix
has
one positive eigenvalue is given
in
Exam-
ple
19.2.11 below. I
We
saw
in
Figure
19.2.7 two
characterizations
for
the
distance
spaces
of
neg-
ative
type.
Winkler
[1985]
proposes
yet
another
characterization
for
the
graphs
of
negative
type,
exposed
in
Theorem
19.2.10 below. Let G
be
a
graph.
Consider
an
orientation
G'
of
G which has, for each edge
(a,
b)
of
G, exactly one
of
the
arcs
(a,
b)
or
(b,
a). Given two arcs e = (a,
b)
and
e' = (a', b')
of
G',
set
(e, e')
:=
~(da(a,
b') -
da(a,
a') - da(b, b') + da(b,
a')).
(This
is
the
same
definition as
the
one considered
later
in
(21.2.13)
up
to
a
factor
2.)
Observe
that,
if
d
a
is
of
negative
type
and
U
a
E R
m
(a E
V)
are
vectors
satisfying
da(a,
b)
=
(II
U
a
- Ub
112)2
for all a, b E
V,
then
(e, e') coincides
with
the
scalar
product
(Ub
-
ua)T(Ub
l
-
ual).
Theorem
19.2.10.
Let
G
be
a connected graph on n + 1 nodes
and
let G'
be
an
arbitrary
orientation
of
G.
Let
T
be
a spanning tree
in
G, with corresponding
arcs
el,
...
,en
in
G'.
The following assertions are equivalent.
(i)
da
is
of
negative type.
(ii) The n x n
matrix
((ei'
ej)
)i,j=l,
...
,n
is positive semidefinite.
Proof. Let V
= {ao, aJ,
...
,an}
denote
the
set
of
nodes
of
G.
By
definition, d
a
is
of
negative
type
if
and
only
if
L
da(ar,as)xrxs
~
0 for all x E
U:=
{x
E R
n
+1
I L
Xr
=
O}.
For
each
node
a
r
E V, set
A(a
r
)
:=
{i E
{I,
...
,n}
I
the
arc
ei
ends
in
a
r
},
B(a
r
):=
{i
E
{I,
...
,n}
I
the
arc
ei
begins
in
arlo
