Deza M.M., Laurent M. Geometry of Cuts and Metrics
Подождите немного. Документ загружается.


302
Chapter
20. Isometric Embeddings
of
Graphs
into
Cartesian
Products
The
relation
fit
can
be
computed
in
time
O(mn) as
it
suffices
to
compare every
of
T
with
the
edges
of
G.
That
the
relations
(J
and
(Jl have
the
same transitive closure follows from
Lemma
20.1.6 below, which shows
that
the
statement
from
Lemma
20.1.2 re-
mains
valid for
the
relation (Jl. Indeed, suppose
that
(Ji has
kl
equivalence
classes:
Ft,
...
,
Fkl'
Then,
k
:::;
kl
as each class
of
(J*
is
a union
of
classes
of
(Ji.
On
the
other
hand,
the
arguments
used
in
the
proof
of
Theorem
20.1.1 show
that
G
'-+
rr~~l
Hh
is a
metric
representation
of
G, where Hh is
obtained
from G by
contracting
the
edges
of
E \ Fh'
This
shows
that
kl
:::;
k. Therefore, k =
kl;
that
is,
(J*
and
(Ji coincide. I
The
following
lemma
was proved by Feder [1992].
Lemma
20.1.6.
Let F
l
,
...
,
Fkl
denote the equivalence classes
of
the
transitive
closure
(Ji
of
the
relation (Jl. Given two nodes a, b
of
G, let P
be
a
shortest
path
from a
to
b,
and
let Q
be
another
path
joining a
to
b
in
G.
Then,
for all
h = 1,
...
, k
l
,
Proof.
Let
P
T
:=
(a
.-
in
the
tree T
and
set Q
j E
{I,
...
, t},
set
ZO,Zl,
...
,Zt
:=
b)
denote
the
path
joining a
and
b
(Yo
a,Yl,···,Yq:=
b).
For i E
{l,
...
,q}
and
/-tij
:=
da(Zj-l,
Yi)
da(Zj-l,
Yi-d
da(zj,
Yi)
+
da(zj,
Yi-d·
Observe
that
/-tij
= 0 if
the
edges
(Zj-l,
Zj)
and
(Yi-lo
Yi)
are
not
in
relation by
(J.
Then,
il(Yi_I,Yi)EE(Q)nF"
E
jl("'j-1>"'j
)EE(PT)
E
/-tij
il(Yi-l
,Yi)EE(
Q)nFh
E
/-tij
il(zj
-I,"'j
)EE(PT
)nF"
il(Yi_
!,y;)EE(Q)nF
h
E E
/-tij
jl(zj
_I
,Zj
)EE(PT
)nFh
il(Yi_l,y;)EE(Q)
E
da(zj-J,
b)
- da(zj--l.
a)
-
da(zj,
b)
+
da(zj,
a).
il(Zj-l,Zj
)EE(PT
)nF"
Setting
P (xo a,
xl.
...
,
xp
:=
b),
we
deduce
that
E da(a,
Xi)
-
da(a,Xi-d
- da(b,
Xi)
+
da(b,Xi-d
il(xi_l,X;)EE(p)nh
E da(a,
Yi)
- da(a, Yi-t) da(b,
Yi)
+ da(b, Yi-l).
il(Yi-l
,y;}EE(
Q)nFh
The
result
now follows as
the
first
term
is equal
to
2IE(p)nFhl
while
the
second
term
is less
than
or equal
to
2IE(Q)
n Fhl. I
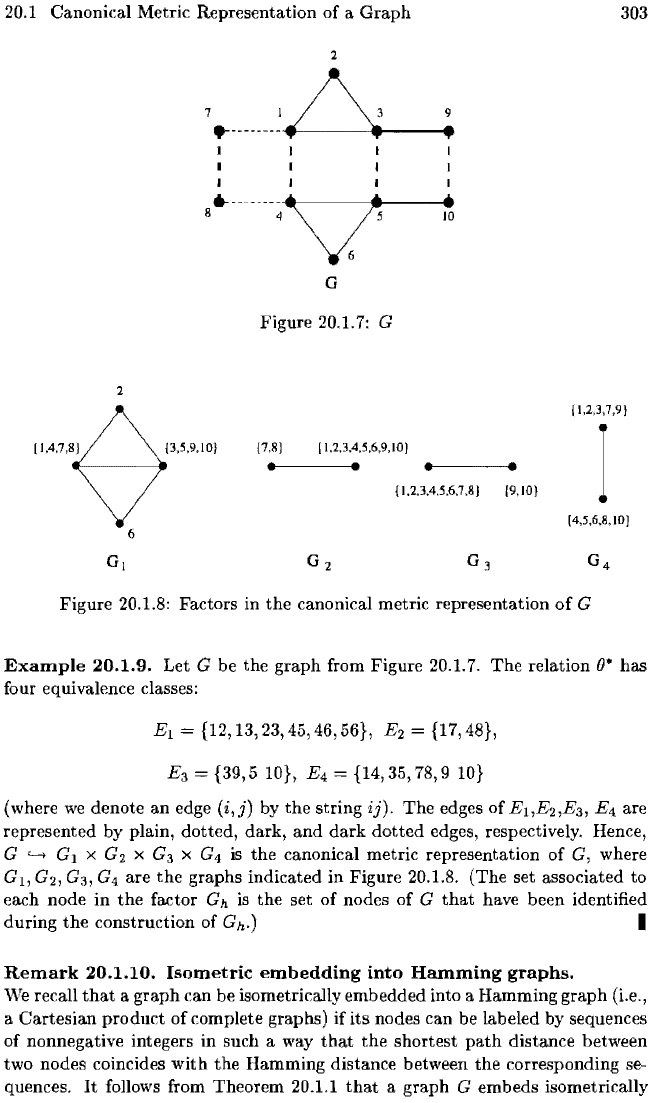
20.1 Canonical Metric Representation
of
a
Graph
303
'.-uu---,6
9
•
I I I I
,·-------,V
•
10
G
Figure 20.1.7: G
2
"""<j"""
(1.2,3,7.9)
{7,8) (1,2,3,4,5,6.9,10)
..
------~.
..------~.
[9.10) (I,2,M.5.6,7,8)
I
(4.5,6,8.1O)
6
Figure 20,1.8: Factors in the canonical metric representation
of
G
Example
20.1.9.
Let G be the graph from Figure 20.1.7.
The
relation
8*
has
four equivalence classes:
El
= {12, 13,
23,
45, 46, 56}, E2 = {17, 48},
E3 = {39,5 10}, E4 = {14, 35, 78, 9
10}
(where
we
denote
an
edge
(i,j)
by
the
string
ij).
The edges of are
represented by plain, dotted, dark,
and
dark
dotted
edges, respectively. Hence,
G
'-t
G
1
X
G
2
X
G
3
X
G
4
is the canonical metric representation of G, where
G
I
,
G
2
,
G
3
,
G
4
are
the
graphs indicated in Figure 20,1.8. (The set associated to
each node
in
the
factor G
h
is
the
set of nodes
of
G
that
have been identified
during
the
construction
of
Gh.) I
Remark
20.1.10.
Isometric
embedding
into
Hamming
graphs.
We
recall
that
a
graph
can be isometrically embedded into a Hamming
graph
(i.e.,
a Cartesian
product
of
complete graphs) if
its
nodes can be labeled by sequences
of
nonnegative integers in such a way
that
the
shortest
path
distance between
two nodes coincides
with
the Hamming distance between
the
corresponding
se-
quences.
It
follows from Theorem 20.1.1
that
a
graph
G embeds isometrically

304
Chapter
20.
Isometric Embeddings
of
into
Cartesian
Products
into a
Hamming
graph
if
and
only if each factor Gh in
the
canonical metric
representation
of
G is a complete graph. (Indeed, let
0: : G
'-;
II
Kq;
l$i$m
be
an
isometric embedding of G into a
Hamming
graph.
We
may
assume
that
0: is
irredundant
since deleting a node from a complete
graph
yields
another
complete graph. Therefore, as complete graphs are irreducible, 0: is
the
canonical
metric representation
of
G.)
the embedding into a
Hamming
graph
is
unique (Winkler [1984]). Moreover, one can recognize whether a
graph
G is
an
isometric
subgraph
of
a
Hamming
graph in polynomial time. For this,
it
suffices
to
determine
the
canonical metric representation of G
and
to
check whether all
its factors are complete graphs.
This
can
be
done
in
time
O(mn)
using Oem)
space (using Feder's algorithm mentioned in Remark 20.1.5). Wilkeit
[1990J
has
proposed earlier
an
algorithm
with
running time
O(n
3
),
which yields moreover
a
structural
characterization for isometric subgraphs of
Hamming
graphs.
As
an
example, consider
the
graph
H from Figure 20.1.11 (taken from Wilkeit
[1990]).
The
relation
0*
has three equivalences classes:
{12, 34, 35, 45},
E2
{28, 37, 56},
and
E3
= {14,
23,
78}.
Hence,
H,-;
K3 X K2 X K2 is
the
canonical metric representation of
H.
We
also
indicate for
the
graph
H in Figure 20.1.11 the sequences from
{O,
1,
2}
x
{O,
I}
2
providing
the
correct labeling
of
the
nodes of
H.
Equivalently, the
path
metric
of
H
can
be
decomposed as
an
integer
sum
of multi
cut
semimetrics, namely,
dH
= 6({1,4}, {2,3, 7,8}, {5,6}) + 6({1,
2,3,4,
5},
{6,
7,8})
H{
{I,
2,
8},
{3,
4,
5,
6, 7}).
(Recall Proposition 4.2.9.)
2lJ
[5.6)
13.4.5.6.7)
111
000
100
110
{lAl
H
!2.3.7.81
11.2.3.4.5) [6.7.8)
-------
factors
of
H
1
11.2.8)
Figure 20.1.11: Embedding graph H
in
a Hamming
graph
I

20.2
The
Prime
Factorization
of
a
Graph
305
20.2
The
Prime
Factorization
of
a
Graph
Let G be a connected graph. A factorization of G is a metric representation
which is
an
isomorphism. G is said to be prime if G cannot be decomposed
as the Cartesian product of two other graphs (each having at least two nodes).
Sabidussi
[19601
proved
that
every connected graph admits a unique prime fac-
torization. Unicity
is
lost for disconnected graphs (see Zaretskii [1965]).
The
graph
factoring problem
can
be
stated
as follows:
Given a connected
graph
G, decide whether G is prime.
If
not, find
the prime factorization
of
G.
This
problem
can
be
solved in time polynomial
in
the
number
of
nodes (Feigen-
baum,
Hershberger
and
Schiiffer
[1985],
Winkler [1987a]).
We
restrict ourselves
to
connected graphs since the
graph
factoring problem for disconnected graphs
is
at
least as
hard
as the
graph
isomorpWsm problem. (Indeed, one
can
determine
whether two graphs G
and
Hare
isomorpWc by checking whether
the
graph
con-
sisting
of
two isolated nodes
is
a factor
of
the
disjoint union
of
G
and
H.)
The
algorithm proposed
by
Feigenbaum, Hershberger
and
Schaffer
[1985]
is
based
on
Sabidussi's original proof and is rather difficult;
it
runs
in
time
O(n
4
.
5
)
where
n
is
the
number
of
nodes of the graph. Winkler
[1987a]
proposes an algorithm
which
is
based on the canonical metric representation
of
graphs presented in
Section 20.1, with running time
O(n
4
).
We
describe briefly
the
main ideas of his
algorithm.
Let G
be
the
connected graph whose prime factorization is
to
be found. Let
(J
: V(G)
--->
II
V(Gh)
l~h~k
denote
the
canonical metric representation
of
G and set
for each node a
E
V.
Set
S:=
{I,
...
, k}. For a subset T of S, let
(JT
denote
the
mapping from V
to
IThET
V(Gh) defined
by
aT(a)
(ah(aJ
I h E
T)
for a E
V.
A
partition
(S1,'
..
,Sm)
of
S is said to be
"goo!!'
if
If
this is
the
case,
then
(J(V)
II
(JSi(V),
19~m
G
II
(JSi(G)
l~i~m
gives a factoring
of
G. In particular, the prime factorization of G corresponds
to
a good
partition
of
S. A subset T of S is said to
be
complete if
(JT(V)
II
V(Gh)'
hET

306
Chapter
20.
Isometric Embeddings
of
Graphs
into
Cartesian
Products
A
subset
T
~
S
can
be checked for completeness
in
polynomial time. If S itself is
complete,
then
G = G
1
x
...
X G
k
is the prime factorization
of
G. Otherwise,
Sis
not complete. One
can
find a
minimum
incomplete subset T
of
S
in
polynomial
time.
(Indeed, check whether all (k
-I)-subsets
of
S are complete.
If
yes,
then
S
is
minimal
incomplete. Else, let T be
an
incomplete (k - I)-subset
of
S.
Check
all
(k - 2)-subsets
of
T,
and
so on.)
The
crucial fact is
that,
if
T is
minimal
incomplete
and
if (S1,
...
, Sm) is a good
partition
of
S,
then
T
~
Si for some
i
E
{I,
...
,
m}.
(If not,
then
Tn
S1,
...
,
Tn
Sm
are complete, from which one
deduces
that
T itself is complete.) Now,
O"r(G)
cannot be split in a factorization
of
G. Hence,
we
may consider
the
metric representation
G
'-+
O"r(G)
x
II
Gh
hES\r
instead
of
the
initial representation G
'-+
fh<h<k Gh.
The
new representation
has
at
most
k - 1 factors (since
ITI
2
2,
as siri"gietons are complete).
We
repeat
the
process
with
this
new representation until
we
find a representation whose
index
set is complete.
This
final representation is
the
prime factorization
of
G.
Feder
[1992]
shows how
this
algorithm can be performed
in
O(mn)
steps using
O(
m)
space; a faster algorithm
running
in O( m log
n)
time
and
using O(
m)
space
is proposed by
Aurenhammer,
Hagauer
and
Imrich
[1990].
20.3
Metric
Decomposition
of
Bipartite
Graphs
We
recall
that
the
semimetric cone METn is defined by
METn
=
{x
E
ffi.(;)
I Xij
-xik
-Xjk
S;
0 for
alli,j,k
E
{I,
...
,n}}.
In
other
words,
MET
n consists
of
all semimetrics on n points. A semimetric
d E
MET
n is
said
to
be primitive
if
d lies on
an
extreme ray
of
MET
n,
i.e.,
if
d =
d1
+ d
2
with
d
1
, d
2
E
MET
n implies
that
d
1
=
0:'1
d, d
2
=
0:'2d
for some
0:'1,0:'2
2
o.
Given d E
MET
n
, let
F(d)
denote
the
smallest face
of
METn
that
contains d.
Hence,
F(d)
consists
of
all
the
vectors Y E METn
that
satisfy
the
same triangle
equalities as
d,
i.e., such
that
Yij -
Yik
- Yjk = 0 whenever dij - d
ik
- djk =
O.
Then,
F(d)
is a simplex face (i.e.,
the
primitive semimetrics lying on
F(d)
are
linearly independent) if
and
only
if
d
admits
a unique decomposition as a
sum
of
primitive semimetrics (recall
Lemma
4.3.2).
Let G be a connected
graph
on n nodes.
Its
path
metric de belongs
to
the
semimetric cone METn. Hence, a
natural
question
to
ask is
what
are
the
possible decompositions of de as a
sum
of primitive semimetrics. Lomonosov
and
Sebo
[1993]
show
that,
if
G is a
bipartite
graph,
then
de
admits
a unique such
decomposition, i.e.,
de
lies on a simplex face of METn.
In
fact,
the
primitive
semimetrics entering
the
decomposition
of
de are gate O-extensions of
the
path
metrics
of
the
factors in
the
canonical metric representation
of
G.

20.3 Metric Decomposition of
Bipartite
Graphs
307
Theorem
20.3.1.
Let
G
be
a connected bipartite graph
on
n nodes
with
iso-
metric
dimension
dimI(G)
= k.
Let
F(da)
denote the
smallest
face
of
the
semi-
metric
cone
METn
that
contains
da.
Then,
F(da)
is a
simplex
face
of
METn
of
dimension
k.
Proof. Let E
b
...
,Ek
denote
the
equivalence classes of
the
relation
(J*
and
let
denote
the
associated canonical metric representation of G. For a node a E V,
denote by
(al,'
..
,ak)
its
image
under
the
canonical embedding. For h =
1,
...
,
k,
let d
h
denote
the
semimetric
on
V defined by
for
a,
bE
V.
Then,
d
can
be
decomposed as
The
semimetrics d
1
,
•••
,d
k
are clearly linearly
independent
and
they
belong
to
the
face
Fa.
We show
that
F(d
a
)
is
generated by
{db"
.
,dd.
For this,
we
show
that
each x E
Fa
is of
the
form x =
Ll<h<k
ahdh
for some scalars
ah
;:::
O.
Let
x E
Fa.
By definition,
this
means
that
every triangle inequality which is satisfied
at
equality by d
a
is also satisfied
at
equality by
x.
We claim
that,
if e =
(a,
b)
and
e' =
(a',b')
are edges of G,
then
e(Je'
===>
x(a,
b)
=
x(a',
b').
Indeed, as G is
bipartite,
we
can suppose
that
a' E
G(a,
b)
and
b'
E G(b, a).
One
can
easily check
that
da
satisfies
the
following four triangle equalities:
d
a
( a' ,
b)
= d
a
( a', a) + d
a
( a, b),
da(
a, b') =
da(a,
b)
+
da(b,
b'),
da(a',
b)
=
da(a',
b') +
da(b,
b'),
and
da(a,
b') =
da(a,
a')
+
da(a',
b').
Hence, x satisfies these four triangle equalities too. From
the
first two equalities,
we
obtain
x(a',
b)
-
x(a,
b') =
x(a',
a) - x(b, b'),
and
the
last two
imply
x(a',b)
-
x(a,b')
=
x(b,b')
-
x(a,a').
Therefore,
x(a,a')
=
x(b,b')
and
x(a,b')
=
x(a',b)
which imply
that
x(a,b)
=
x(a',
b'). Hence,
there
exist scalars
al,
...
,ak
;:::
0 such
that
x(
a,
b)
=
ah
for each
edge
(a,
b)
in
the
class Eh. We show
x = L
ahdh·
l:'Oh9

308
Chapter
20. Isometric
Embeddings
of
Graphs
into
Cartesian
Products
Let
a,b
E V
and
let
P:=
(ao
=
a,al,
...
,ap =
b)
be
a
shortest
path
from a
to
b
in
G.
Set
Nh
:=
IE(P) n Ehl for h = 1,
...
,k.
Using
the
triangle
equalities along
P,
one
obtains
x(a,b)
= L
x(ai-l,ai)
= L
OOhNh·
l:;i:;p
l:;h:;k
As P
contains
Nh edges from Eh, by
contracting
the
other
edges
of
P,
we
obtain
in
the
graph
G
h
a
path
from
ah
to
bh
oflength
N
h
.
This
shows
that
d
ah
(ah,
bh)
::;
Nh.
Let
Q'
be
a
shortest
path
from
ah
to
bh
in G
h
.
SO,
Q' arises from a
path
Q
joining
a
to
bin
G. By
Lemma
20.1.2, Q contains
at
least Nh edges from Eh.
Therefore,
IQ'I
2:
N
h
, implying
that
d
ah
(ah'
bh)
= Nh. Hence,
L
oohdh(a,
b)
= L
OOhNh
= x(a,
b).
l:;h:;k l:;h:;k
So, we have
shown
that
F(da)
is
generated
by {d
1
,
...
,dd.
Therefore,
F(da)
is
a
simplex
face
of
dimension k of
METn.
I
Corollary
20.3.2.
Let
G
be
a connected bipartite graph. Then, its path
met-
ric
da
lies on an extreme ray
of
the
semimetric
cone
METn
if
and only
if
dim]
(G) = 1,
i.
e.,
if
G is irreducible. I
Corollary 20.3.2 is
not
valid for
nonbipartite
graphs. For instance, K3 is irre-
ducible,
but
its
path
metric
lies in
the
interior
of
the
semimetric
cone
MET
3
.
20.4
Additional
Notes
Several
further
aspects
of
the
metric
structure
of
graphs
have received a consid-
erable
attention
in
the
literature,
leading
to
rich theories. For instance, distance-
regular
graphs,
or
strongly
regular
graphs,
are
defined
by
some invariance
prop-
erty
of
their
path
metric.
The
study
of these
graphs
leads
to
a large
and
rich
area
of
research,
connected
to
algebraic
graph
theory.
The
monograph
by Brouwer,
Cohen
and
Neumaier
[1989] is
an
excellent source
of
information
on
this
topic.
Let
us
only
remind
that
some results along
this
line have
been
presented
in
Part
II, especially
in
Chapter
17, where
hypermetric
graphs
are considered.
The
pa-
pers
by
Koolen
[1990, 1993, 1994]' Koolen
and
Shpectorov [1994], Weichsel [1992]
deal
with
the
study
of
graphs
with
high
regularity
that
have some specified
met-
ric
properties
such as hypermetricity, or some special cases of
it
(e.g., satisfying
the
pentagonal
inequality,
or
the
hexagonal inequality), etc. For instance,
the
distance-regular
graphs
that
are
hypercube
embeddable
are completely classified:
they
are
the
hypercubes,
the
even circuits,
and
the
double-odd
graphs
(Koolen
[1990], Weichsel [1992]).
The
distance-regular
graphs
that
are of negative
type
(or, equivalently,
hypermetric)
are classified
in
Koolen
and
Shpectorov [1994];
see
Theorem
17.2.7.
In
this section we
mention
some
further
topics related to
the
metric
structure
of
graphs.
Among
them,
the
study
of
graphs
having specified
metric
properties
(e.g., interval-regular graphs, geodetic graphs)
and
the
question
of
embedding

20.4
Additional
Notes
309
an
arbitrary
distance
space into a (weighted)
graph.
There
is a vast
literature
on
these topics. So,
we
shall
not
attempt
to give a detailed
treatment;
we
only
mention
without
proof
some facts, results
and
references.
Interval-Regular
Graphs
and
Geodetic
Graphs.
Let
G =
(V,
E)
be
a
connected
graph.
For two nodes x, y E V, let
,(x,
y) denote
the
number
of
shortest
paths
joining
x
to
y
in
G.
Set
I(x,y):=
{z E V I dG(x,y) = dG(x,z)
+dG(z,y)}.
Moreover, for i =
0,1,
...
,dG(x, y), set
Ni(X,y):=
{z E
I(x,y)
I dG(x,z)
=i}
and
N_
1
(x,y):=
{z
E V I dG(x,z) = 1
and
dG(z,y) = dG(x,z) + I}.
Then,
G is
distance-regular
if
the
numbers
IN1
(x,
y)1
and
IN_1
(x,
y)1
depend
only
on
dG(x,y).
The
graph
G is said
to
be
interval-regular
if
IN
1
(x,y)1 = dG(x,y)
for all nodes
x,
y E V (see Mulder [1980, 1982]); G is said
to
be
uniformely
geode-
tic (in Cook
and
Pryce
[1983]) (or F -geodetic
in
Ceccherini
and
Sappa
[1986])
if
,(x,
y)
depends
only
on
dG(x, y). Every distance-regular
graph
is uniformely
geodetic (Cook
and
Pryce
[1983]),
and
every
Hamming
graph
is interval-regular
(since
the
subgraph
induced
by
the
interval
I(x,
y) is isomorphic
to
the
dG(x, y)-
hypercube).
See, e.g., Scapellato [1990]
and
Koolen [1993] for more
information
on
uniformely geodetic graphs; Koolen [1993] characterizes
the
uniformely geode-
tic
bipartite
graphs.
Several
characterizations
of
the
hypercube
are
known. Foldes [1977] shows
that
the
hypercube
is
the
only connected
bipartite
graph
for which
,(x,y)
=
dG(x,y)! holds for any
pair
of
nodes. Ceccherini
and
Sappa
[1986] show
that
a
connected
bipartite
graph
G is isomorphic
to
a
hypercube
if
and
only
if
the
Cartesian
product
G x K2 is uniform ely geodetic.
Interval-regular
graphs
are
linked
to
hypercubes
in
the
following way: Mul-
der
[1982] shows
that
a connected
graph
G is interval-regular
if
and
only if, for
any
two nodes
x,
y,
the
subgraph
of
G consisting
of
the
edges connecting two
consecutive levels
Ni(x,y)
and
N
i
+
1
(X,y)
(i =
O,l,
...
,d
G
(x,y)
-1)
is isomor-
phic
to
the
d
G
(x,
y)-hypercube. Equivalently, G is interval-regular
if
and
only
if
,(x,y)
= dG(x,y)! for all nodes X,y E
V.
Hamming
graphs
can
be
characterized
in
terms
of
interval-regular
graphs
in
the
following way
(Bandelt
and
Mulder [1991]): A connected
graph
G is
a
Hamming
graph
if
and
only
if
G is
an
interval-graph, G does
not
contain
K 1,1,2 as
an
induced
subgraph,
and
the
only isometric
odd
circuits
in
G are
triangles. More generally,
Bandelt
and
Mulder [1991] characterize
the
connected
graphs
that
can
be
decomposed as a
Cartesian
product
where each factor is
the
310
Chapter
20.
Isometric Embeddings
of
Graphs into Cartesian
Products
suspension
of
a geodetic graph of diameter
at
most
2.
(A geodetic
graph
is a
graph in which there
is
exactly one shortest
path
joining any
pair
of
nodes.)
Embedding
Metrics
into
Graphs.
We
now consider the question of embed-
ding metrics into graphs or, more generally, into weighted graphs.
This
topic
has many applications in various areas, such as psychology (Cunningham
[1978])
and
biology (Penny, Foulds
and
Hendy [1982]).
Let G
= (V,
E)
be
a
graph
and
let
We
E ll4 (e E
E)
be nonnegative weights
assigned to its edges.
The
path
metric
da,w
of the weighted graph (G,w)
is
defined by letting da,w(x,
y)
denote the smallest value
of
LeEE(P)
We,
taken over
all
paths
P joining x
and
y in G.
Given a finite metric space
(X,d), one says
that
the
weighted graph (G,w)
realizes
(X,
d)
if there exists a mapping i
EX
f--->
Xi
E V such
that
for all
i,j
E
X.
The
graph G may have more nodes
than
those corresponding to
points
of
X.
Every metric space
can
clearly be realized by some graph, namely,
by
the
complete graph on
IXI
nodes with weights
d(i,j)
on its edges. Consider,
for instance,
the
metric d on X
{I,
2,
3}
defined
by
d(1,2) =
4,
d(1,3) =
8,
d(2,3) = 6. Then, d can be realized by
the
following two weighted graphs:
K3
and
a tree
with
one auxiliary node.
3
The
objective is, therefore, to find a graph
(G,
w)
realizing (X,
d)
whose
total
weight
We
is as small as possible.
The
existence of
an
optimal realization,
i.e., with minimum
total
weight among all possible realizations, was shown in
Imrich, Simoes-Pereira
and
Zamfirescu
[1984].
But
finding an optimal realiza-
tion
is
an
NP-hard
problem even if
the
metric is assumed to be integer valued
(AlthOfer
[1988],
Winkler [1988]).
On
the
other
hand, the metric spaces
that
can be realized by weighted trees
are well characterized; such graphs have been introduced earlier under
the
name
of
tree metrics. Namely, (X,
d)
is
realizable by a weighted tree, if
and
only
if
d
satisfies
the
following condition, known as the four-point cond·ition:
d(i,j)
+ d(r,
8)
::;
max(d(i, r) + d(j,
8),
dei,
8)
+ d(j, r)),
i.e.,
the
two largest of the three sums d(i,j)+d(r,
8),
dei,
r )+d(j, s),
dei,
s)+d(j, r)
are equal, for all
i,j,r,s
E X (Buneman [1974]). Note
that
the
four point

20.4
Additional
Notes
311
condition implies
the
metric condition (by taking r s). Moreover, if (X,
d)
is
realizable by a tree,
then
there
is only one such realization;
it
is
optimal
among
all
graph
realizations,
and
it
can
be
found
in
polynomial
time
(Hakimi
and
Yau
[1964]).
The
four
point
condition is closely
related
to
another
metric condition, namely,
ultrametricity. Recall
that
a distance space
(X,
d)
is said
to
be
ultrametric
if
it
satisfies
d(i,j):S;
max(d(i,k),d(j,k»
for all
i,j,
k E
X.
In
other
words, any
three
points form
an
isosceles triangle
with
the
third
side
shorter
than
or
equal
to
the
other
two. See Aschbacher,
Baldi,
Baum
and
Wilson
[1987]
for applications
and
references
on
ultrametrics.
Clearly, every
ultrametric
space satisfies
the
four point condition. Actually, each
tree
metric
can
be
characterized
in
terms
of
an
associated
ultrametric
in
the
following way
(Bandelt
[1990]). Let
(X,
d)
be
a distance space, let
rEX,
and
let c be a
constant
such
that
c
?:
max(d(i,j)
I
i,j
E
X).
Define
the
distance
d(c)
on X \ {r} by
setting
d(c)(i,j)
:=
c +
~(d{i,
r) + d(j, r) - d{i,j»
for i
::/=
j
EX.
Then,
d
is
a tree metric if
and
only
if
d(
c) is ultrametric.
Ultrametrics
have also a tree-like representation, which is used in classification
theory,
in
particular,
in
taxonomy (see Gordon
[1987]
and
references therein for
details).
Let
T = (V,
E)
be
a tree
and
We
E ll4
(e
E
E)
be
nonnegative weights
on its edges.
Let
rEV
be a specified node
(a
root)
of
T
and
let X = {Xl,
...
,X,,}
denote
the
set
of
leaves (nodes
of
degree 1)
of
T
other
than
r.
We
assume
that
dT,w(r,
x)
= h for all x E
X,
for some constant h, called
the
height
of
T.
Then,
T is also called a dendrogram,
or
indexed hierarchy.
The
height h( v)
of
a node v
of
T is defined as
the
length
of
a
shortest
path
joining v
to
some leaf
of
X.
Then,
one
can
define a
metric
space
(X,
dx)
on
X by
letting
dx(x,
y)
denote
the
height
of
the
first predecessor
of
x
and
y.
The
metric space
(X,
dx)
is
ultrametric
and
every
ultrametric
arises
in
this
way.
Moreover,
the
distance spaces
(X,
dx)
and
(X,
~dT,w)
coincide.
