Deza M.M., Laurent M. Geometry of Cuts and Metrics
Подождите немного. Документ загружается.

258
Chapter
17.
Hypermetric Graphs
1
1
-I
1 1
1
-111
I
I
I I
---
-~
-2
•
• • •
•
-----
1
1 -2 2
-I
1
1
-2
2
-2
1
-I
S4
S5
S6
1
-1
1
1
I
I
T
T
i
•
• • •
• • • •
• •
•
• •
1
-2
2
-2
2
-I
1 1 -2
2
-2
2
-2
1 -I
S7
S8
-I
(I
-I 2 -3 2
-I I
-2
3
2
• •
• •
-J
T6
T7
-3
:(:-'
-I~
-I
-2
3
-4 4
• 1
•
•
•
•
• •
1 1
J 1
I
Tg
K
I
,5+
K
I
-I -I
M
\
-\
1
rr
-\
\
V
I
-1
I -I
vi
-I
II
-I
I i
I '
-1
I -I
·1
1
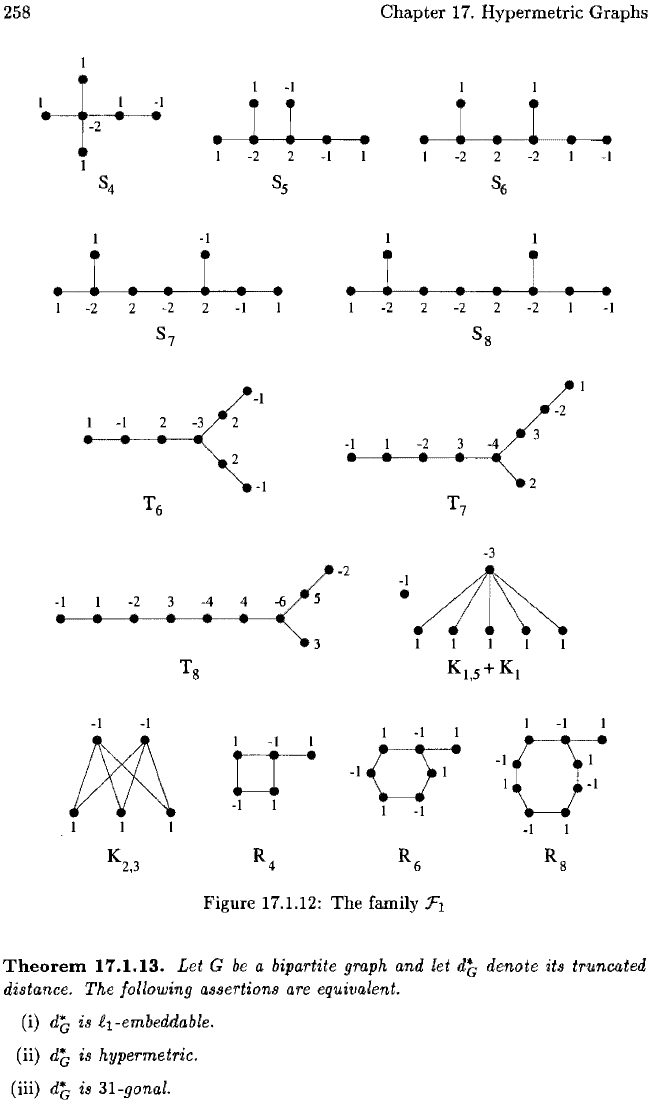
Figure 17.1.12: The family
F1
Theorem
17.1.13.
Let
G
be
a bipartite graph and let
do
denote its truncated
distance. The following assertions are equivalent.
(i)
do
is .e1-embeddable.
(ii) do is hypermetric.
(iii)
do
is 31-gonal.

17.1 A
Characterization
of
Hypermetric
and
C1-Graphs
259
(iv) G does
not
contain
as
an
induced subgraph
any
of
the
thirteen
graphs
from
the
family
F1
shown
in
Figure 17.1.12.
(v) G is a
star
(i.e., G = K1,n for
some
n
~
1),
or
every connected
component
of
G is an induced subgraph
of
an
even circuit C
2n
(n
~
2)
or
of
one
of
the
graphs
Dn
(n
~
4), E
8
,
E
7
,
E6
shown
in
Figure 17.1.11. I
The
proof
of
Theorem
17.1.13 relies
on
several lemmas.
Lemma
17.1.14.
Let
G1(Vl, E
1
)
and
G
2
(V
2
, E
2
)
be
two graphs with
disjoint
node
sets
and
let G denote
their
clique O-sum, with node
set
V
1
U
V2
and
edge
set
E1 U E
2
.
If
the
truncated distance d
Ci
of
G
i
admits
an
C1-embedding
of
size
S;
4
for
i =
1,2,
then
the truncated distance d
c
of
G also
admits
an C1-embedding
of
size
S;
4.
Proof·
Say,
dc,
= L:sc;v,
as8(5)
where
as
~
0 for all 5
and
L:s
as
= 4 (if
L:s
as
S;
4 one
can
make
this
sum
equal
to
4 by
introducing
the
empty
cut
with
coefficient 4 -
L:s
as
in
the
decomposition). Similarly, d
C2
= L:TC;V2/3r8(T)
where
{3T
~
0 for all T
and
L:T
(3T
=
4.
Then,
one
can
verify
that
d
admits
the
following decomposition:
1
d
c
=
8"
L L as{3T[8(5 U
T)
+ 8(5 U
(V2
\ T))]
SC;V,
TC;V2
with
size!
L:S,T as{3T =
4.
I
We
need
a
result
concerning generalized line graphs.
These
graphs
are
defined
in
the
following
manner.
Let H
be
a
graph
with,
say,
node
set {V1,'
..
, v
n
}
and
let a1,
...
,an
be
nonnegative integers. For every
node
Vi
of H consider a cocktail-
party
graph
Kai
x2
(all
being
defined
on
disjoint
node
sets).
Then,
the
generalized
line graph
L(H;
a1,
...
,an)
is
obtained
by
juxtaposing
the
line
graph
L(H)
of
H,
the
n
cocktail-party
graphs
K
aix2
,
and
adding
for every
node
e
:=
ViVj
of
L(H)
(corresponding
to
an
edge e
in
H)
edges between e
and
all nodes of K
aix
2
and
Kaj
x2'
Hence we
obtain
usual
line
graphs
when
a1
= ... = an =
O.
Line
graphs
and
cocktail-party
graphs
have
an
C1-embeddable
truncated
distance; Assouad
and
Delorme
observed
that
this
extends
to
generalized line
graphs
of
bipartite
graphs.
Lemma
17.1.15.
If
H is a bipartite graph,
then
the
truncated distance
of
any
generalized line graph
of
H
admits
an C1-embedding
of
size
S;
4.
Proof.
Let
V = {V1'
...
, v
n
}
= 5 U T
denote
the
bipartition
of
H.
Given integers
a1,
...
,an
~
0, we consider
the
generalized line
graph
L(H;
a1,'
..
,an)
and
we
let
Y
Vi
U
Y~i
denote
the
node
set
on
which
the
cocktail-party
graph
K
aix2
is
defined.
Let
v(a),
Yv~a)
(a
=
1,2,3,4)
be
four disjoint copies of
the
sets
V
and
Y
Vi
(i = 1,
...
,n).
We now consider two
cocktail-party
graphs
G
1
and
G
2
,

260
Chapter
17.
Hypermetric
Graphs
n
G1
being
defined
on
the
node
set
U
(v(<»
u U
Yv~<»)
and
G
2
being
defined
<>=1,2
i=l
n
on
U
(v(<»
u U
Yv~<»)
(with
the
obvious
pairing
for
opposite
nodes). We
<>=3,4
i=l
now
construct
an
isometric
embedding
of
L(H;
a)
equipped
with
the
truncated
distance
into
the
Cartesian
product
of
G1
and
G
2
.
Namely,
to
a
node
ViVj
of
L(H)
(where
Vi
E
Sand
Vj
E
T),
assign
the
pair
(v?),v;3));
to
a
node
y E Y
Vi
(resp. y E
Y~,)
with
Vi
E S, associate
the
pair
(v?),y(3)) (resp.
(v~1),y(4)));
to
a
node
y E Y
Vi
(resp. y E
Y~,)
with
Vi
E
T,
associate
the
pair
(y(l), vP)) (resp.
(y(2),
v~3))).
The
result
now follows since a
cocktail-party
graph
is
£l-embeddable
with
size
2,
which implies
that
the
Cartesian
product
of
two
cocktail-party
graphs
has
an
£l-embedding
of
size 4. I
Lemma
17.1.16.
For each
of
the graphs C
2n
(n
2:
2),
Dn
(n
2:
4), E
6
,
E
7
,
E
s
,
the
truncated
distance
admits
an
£1
-embedding
of
size::; 4.
Proof.
For C
2n
and
Dn,
the
result
follows
by
applying
Lemma
17.1.15.
This
is
obvious for
C
2n
as C
2n
=
L(C
2n
).
On
the
other
hand,
Dn
can
be
obtained
as
an
induced
subgraph
of
the
line
graph
L(C
2m
;
a)
of
some even
circuit
choosing
a
with
all zero
components
except two
equal
to 1. We now
indicate
explicit
£1-
embeddings
for
the
truncated
distances
of
E
6
,
E
7
,
Es
(using
the
node
labelings
shown
in
Figure
17.1.11),
of
respective sizes 3,4,4:
2di6 = b({1,2,5})
+b({1,4,5})
+b({1,2,7})
+b({4,5,7})
+b({1,6,7})
+b({5,6,7});
2di7
= b({1,2,5, 7,8})
+b({1,2,3,4,8})
+b({1,6,8})
+b({2,3,6})
+b({1,2})
+b({4,5})
+b({7})
+b({8});
2dis
= b({1,2,5,
7})
+b({1,2,3,4})
+b({1,6})
+b({2,3,6})
+b({1,2,8,9})
+b({4,5})
+b({9})
+b({7,8}).
I
Proof
of
Theorem
17.1.13.
The
implications
(i)
===}
(ii)
===}
(iii) are obvious.
The
implication
(iii)
===}
(iv) relies
on
the
fact
that
each
of
the
graphs
G E
Fl
has
a
nonhypermetric
truncated
distance.
That
is,
there
exists
an
integer
vector
b
with
L:i
bi
= 1 such
that
Q(b)T
de
>
O.
Explicit
values for b
are
indicated
for
each
graph
of
F1
in
Figure
17.1.12.
Note
that
L:i
Ibil
::;
31
with
equality
for
graph
Ts.
The
implication
(v)
===}
(i) is
immediate.
Indeed,
de
is obviously
£l-embeddable
if
G is a
star
and
otherwise
the
assertion
follows from
Lemmas
17.1.14
and
17.1.16.
We
now
show
the
last
implication
(iv)
===}
(v).
Let
G
be
a
bipartite
graph

17.1 A
Characterization
of
Hypermetric
and
£1-Graphs
261
not
containing
any
of
the
thirteen
graphs
from Figure 17.1.12 as
an
induced
subgraph.
We
first claim
that
(a) every
connected
component
of
G is a tree or
an
even circuit.
Indeed
suppose
that
H is a connected
component
of
G which is
not
a
tree
nor
a
circuit.
Let
C
be
an
induced
circuit
in
H
of
minimum
length;
thus,
101
~
4
and
is even.
There
exists a node x outside C
adjacent
to
some node
of
C.
In
fact,
if
101
~
6,
then
x is
adjacent
to
exactly one
node
of C (by
minimality
of
101);
then
we find R
6
,
Rs
or
T7
as
an
induced
subgraph
of
H
if
ICI
=
6,8
or
~
10,
respectively.
If
101
= 4
and
x is
adjacent
to
only one
node
of
C,
then
we
find
R4
and,
if
ICI
= 4
and
x is
adjacent
to
2 nodes
of
C,
then
we
find K
2
,3.
Thus,
(a)
holds.
If
G
has
a
node
of
degree
~
5,
then
G is
connected
(else,
we
find K
1
,5
+
Kl
as
an
induced
subgraph
of
G) and, moreover, G is a
star
(else,
we
find
S4).
We
can
now suppose
that
G has
maximum
degree
:S
4.
Let
H
be
a
connected
component
of
G
with
maximum
degree ,6., which is a tree;
we
show
that
H
is
an
induced
subgraph
of
15n,
E
6
, E
7
, or
Es.
If,6.
:S
2
then
H is a
path
and,
thus,
is
contained
in
15n.
If,6.
= 4
then
H = K
1
,4
=
15
4
(else
we
find
S4
as
induced
subgraph).
We
now suppose
that
,6.
=
3.
Let
x
be
a
node
of
degree 3
in
H,
let L
1
,
L2, L3 denote
the
connected
components
of
H\x
and,
for
i =
1,2,3,
let
mi
denote
the
longest geodesic
distance
from x
to
a node in Li.
Say, 1
:S
ml
:S
m2
:S
m3· Observe
that
m3
~
3
==}
ml
= 1 (because
of
T6),
m2
~
3
==}
m3
= 3 (because
of
T7),
ml
= 1
and
m3
~
6
==}
m2
= 1 (because
of
Ts).
We
distinguish
two cases.
Case
1:
There
exists a
node
x
of
degree 3 in H for which
m2
~
2.
Then,
in
view
of
the
above observations,
the
only possibilities for
(ml,m2,m3)
are
the
following sequences: (1,2,2), (2,2,2), (1,3,3), (1,2,3), (1,2,4)
and
(1,2,5). Now
H
has
no
node
outside
L1
U
L2
U L3 (else one would find one
of
the
forbidden
induced
subgraphs)
and,
thus,
H is
an
induced
subgraph
of
E6,
E7
or
Es.
Case
2:
Every
node
of degree 3
in
H
has
m2
= 1.
Then,
we
obtain
that
H is
an
induced
subgraph
of
some
15n.
I
On
the
other
hand,
there
is no finite
point
criterion, analogue
to
Theorem
17.1.13, for
truncated
distances
of
general graphs. Indeed, for every n
~
2,
there
exists a
graph
G on
2n
+ 1 nodes whose
truncated
distance
is
not
hy-
permetric
while
the
truncated
distance
of
any
proper
induced
subgraph
of
G
is £1-embeddable. We
present
in
Example
17.1.17 below
an
example
of
such
graph,
taken
from Assouad
and
Delorme [1982]. We
state
a
preliminary
result
for generalized line graphs.
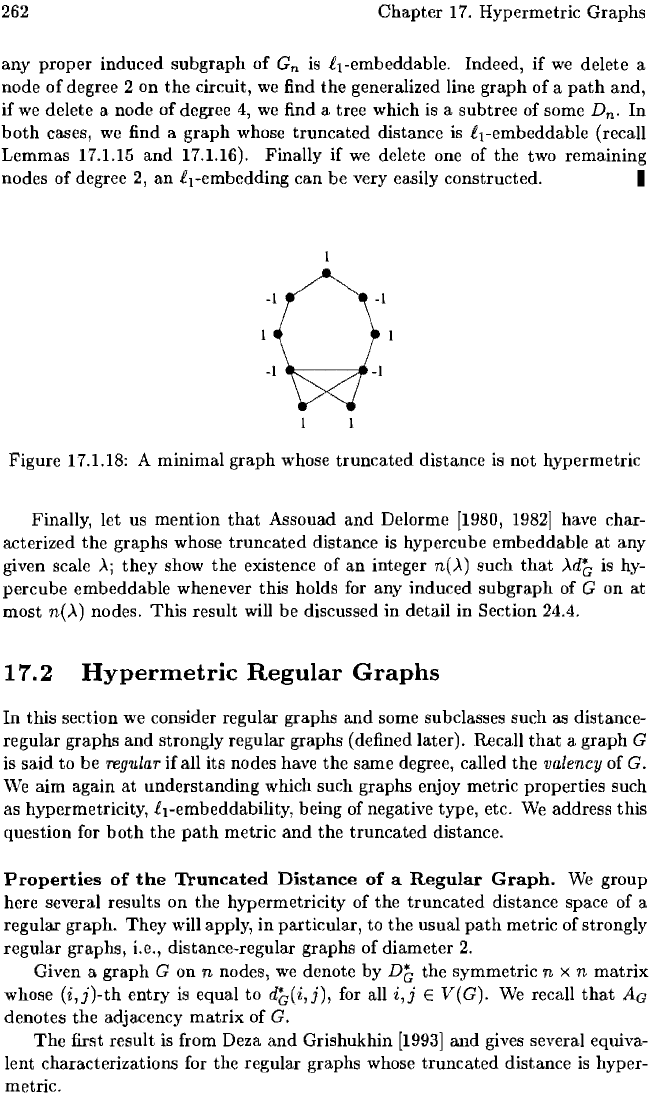
Example
17.1.17.
Let
G
n
denote
the
generalized line
graph
L(C
2n
-
b
a), where
C
2n
-
1
is
the
circuit
on
2n - 1 nodes
and
a
:=
(1,0,
...
,0).
Figure 17.1.18 shows
the
graph
G
4
on
9 nodes.
The
truncated
distance
of
G
n
is
not
hypermetric
(as
it
violates
the
pure
hypermetric
inequality where
the
±1 coefficients are assigned
as
indicated
in
Figure
17.1.18).
On
the
other
hand,
the
truncated
distance
of
262
Chapter
17.
Hypermetric Graphs
any
proper
induced subgraph
of
G
n
is
it-embeddable. Indeed,
if
we
delete a
node
of
degree 2 on the circuit,
we
find the generalized line graph
of
a
path
and,
if
we
delete a node
of
degree
4,
we
find a tree which is a subtree of some Dn.
In
both
cases,
we
find a graph whose truncated distance
is
it-embeddable (recall
Lemmas 17.1.15 and 17.1.16). Finally if
we
delete one of the two remaining
nodes
of
degree
2,
an
it-embedding can be very easily constructed. I
Figure 17.1.18: A minimal graph whose truncated distance
is
not hypermetric
Finally, let us mention
that
Assouad and Delorme
[1980,
1982]
have char-
acterized
the
graphs whose truncated distance
is
hypercube embeddable
at
any
given scale
).j
they
show the existence
of
an
integer n().) such
that
)'d
o
is
hy-
percube embeddable whenever this holds for any induced subgraph of G on
at
most n().) nodes. This result will be discussed
in
detail in Section 24.4.
17.2
Hypermetric
Regular
Graphs
In
this section
we
consider regular graphs
and
some subclasses such as distance-
regular graphs and strongly regular graphs (defined later). Recall
that
a graph G
is said
to
be regular
if
all its nodes have
the
same degree, called the valency of G.
We
aim again
at
understanding which such graphs enjoy metric properties such
as hypermetricity, it-embeddability, being of negative type, etc.
We
address this
question for
both
the
path
metric
and
the truncated distance.
Properties
of
the
Truncated
Distance
of
a
Regular
Graph.
We
group
here several results on the hypermetricity of the truncated distance space of a
regular graph. They will apply,
in
particular, to the usual
path
metric of strongly
regular graphs, i.e., distance-regular graphs of diameter
2.
Given a graph G on n nodes,
we
denote by
Do
the symmetric n x n matrix
whose
(i,j)-th
entry
is
equal
to
dG(i,j),
for all
i,j
E
F(G).
We
recall
that
Ao
denotes
the
adjacency matrix of
G.
The
first result is from Deza
and
Grishukhin
[1993]
and gives several equiva-
lent characterizations for the regular graphs whose truncated distance is hyper-
metric.

17.2 Hypermetric Regular Graphs
263
Proposition
11.2.1.
Let
G
be
a connected regular graph
on
n nodes with valency
k.
The following assertions are equivalent.
(i) d
c
is
of
negative type.
(ii) the distance space
(V(G),2d
c
)
has a spherical representation with radius
r satisfying
r2
< 2.
(iii) d
c
is hypermetric.
(iv) '\7G is
of
negative type.
(v) .Amin(Ac)
~
-2.
(vi)
Dc
has exactly one positive eigenvalue.
Moreover,
if
d
c
is hypermetric, then the radius r
of
the
Delaunay
polytope asso-
ciated with the space
(V
(G), 2d
c
)
is given by
(17.2.2)
Proof. (i)
===}
(ii) Note
that
2:
2d
c
(
i,
j)
= 2(2n - 2 - k) is a constant. Hence,
iEV(C)
by
Proposition
14.4.1,
(V
(G), 2d
c
)
has a spherical representation whose radius
r is given by relation (14.4.2). Therefore,
r2
= 2 -
~
and, thus,
r2
<
2.
The
implication (ii)
===}
(iii) follows from Proposition 14.4.4.
(iii)
===}
(iv) By Proposition 14.4.3, the radius of the Delaunay polytope as-
sociated
with
(V(G),2d
c
)
is given by (17.2.2). Since
(V('\7G),2dV'c)
is
the
spherical 2-extension of the space
(V(G),2d
c
),
we
deduce from
Lemma
14.4.5
that
(V
('\7
G),
dV'c) is of negative type.
The
equivalence (iv)
{==>
(v) follows from Proposition 17.1.4.
(v)
===}
(vi) Let
.AI
= k,
.A2,
...
,.An
~
-2
denote
the
eigenvalues of
the
adjacency
matrix
Ac
of
G. Note
that
Dc
=
2J
-
(Ac
+ 21),
where J is
the
n x n
matrix
of all ones.
The
vector of all ones is a common
eigenvector of
Ac
and
Dc
for
the
eigenvalues k
and
2n
- 2 - k, respectively. One
checks easily
that
the
other
eigenvalues of
Dc
are
-.A2
-
2,
...
, -.An - 2 which
are all nonpositive. Hence,
2n
- 2 - k is
the
only positive eigenvalue of
Dc.
The
implication (vi)
===}
(v) follows by reversing
the
arguments used above for
the
implication (v)
===}
(vi). Using
the
obvious implication (iv)
===}
(i),
we
obtain
the
equivalence of (i)-(vi). I
Proposition
17.2.1 applies, in particular, to
the
regular graphs of
diameter
2;
then,
the
two distances
dc
and
d
c
coincide. However, without
the
regularity
assumption,
the
equivalence of (i)-(vi) does not hold. For instance,
Kg
\ P
3
has
diameter
2,
is not regular, satisfies (v)
but
not (iii) (recall Example 14.4.9).

264
Chapter
17.
Hypermetric
Graphs
Let G
be
a connected regular
graph
with
Amin(Ac)
:::::
-2.
Hence, its
trun-
cated
distance
d'G
is
hypermetric. Let
Pc
denote
the
Delaunay polytope asso-
ciated
with
the
space (V(G),2d'G)
and
let
He
denote its I-skeleton graph.
By
Proposition
14.3.3, (V(G),d'G)
is
an
isometric subspace of
the
graphic
metric
space
(V(He),d
Hc
).
By
Proposition
14.3.5,
Pc
is a Delaunay
polytope
in
a
root
lattice
and,
thus,
He
is
a direct
product
of some of
the
Delaunay
polytope
graphs
shown
in
Figure 14.3.1.
The
next result from Deza
and
Grishukhin
[1993]
shows
that,
if
He
is a nontrivial direct
product,
then
it
can
only be
the
direct
product
of two complete graphs.
A
bipartite
graph
B
with
bipartition
VI
U V
2
of
its
set of nodes is said to be
semiregular if all nodes
in
VI
(resp. all nodes
in
V
2
) have
the
same
degree.
Lemma
17.2.3.
Let G
be
a connected regular
graph
on n nodes with valency
k. Suppose that
Amin(Ac)
:::::
-2
and let
He
denote the 1-skeleton
graph
of
the
Delaunay polytope
Pc
associated with (V( G),
2d'G).
If
He
is
a nontrivial direct
product, then
He
=
Knl
x
Kn2
for some
nl,
n2
:::::
1,
G
is
the line
graph
of
a
bipartite semiregular
graph
and
Proof.
Suppose
that
H
is
the
nontrivial direct
product
HI x H
2
.
By
the
assump-
tion,
(V(G),
d'G)
is
an
isometric subspace
ofthe
graphic metric space
(V(H),
dH).
Let
f:
i E
V(G)
f--+
f(i)
=
(h(i),h(i))
= (il,i2) E
V(Hd
x
V(H
2
)
denote
this
isometric embedding. For i E V (G), set
VI(i)
:=
{j
E
V(G)
I
h(i)
=
h(j)},
V
2
(i)
:=
{j
E
V(G)
I
h(i)
=
h(j)}·
If
i,j
are
adjacent
in
G,
then
j E
VI
(i) U V
2
(i). Conversely,
we
check
that,
if
!VI(i)l,
!V2(i)1
>
1,
then
both
VI(i)
and
V
2
(i) induce a complete
graph
in
G.
For this, let j E VI(i)
and
h E V
2
(i)
with
j
i=
i, h
i=
i.
Then,
(since i
l
=
jl
and
i2
= h
2
)
which is equal to
d'G(i,
h)
+ d'G(i,j)
:::::
2.
This
implies
that
d'G(i,
h)
= d'G(i,j) =
1,
i.e.,
both
hand
j are adjacent to i. One deduces
easily
that
any
two nodes
in
VI,
or
in
Vi,
are adjacent.
Therefore,
if
!VI(i)l,
!V2(i)1
>
1,
then
!VI
(i) I +
!V2(i)
I = k +
2.
For j E VI(i),
VI
(i) = VI(j), k + 2 S !VI(j) I + !V2(j)
I,
implying
that
!V2(i)1
S !V2(j) I
and,
thus, !VI(j)I,
!V2(j)1
> 1, yielding
k + 2 = !VI(j) I + !V2(j) I
and,
thus, !V2(j) I =
!V2(i)l·
Therefore, since G
is
connected,
there
exist integers
p,
q
:::::
1 such
that
!VI
(i)1
=
p,
!V2(i)1
= q for all i E
V(G).

17.2
Hypermetric
Regular
Graphs
265
Let
B
denote
the
bipartite
graph
with
node
bipartition
VI
U V
2
,
where
and
two nodes i
1
E VI,
i2
E V
2
are
adjacent
in
B
if
(i
l
,i2)
=
f(i)
for some
node
i E
V(G).
So each
node
of
VI
(resp. of V
2
)
has valency p (resp. q), i.e., B is
semiregular.
It
is
immediate
to
see
that
G is
the
line
graph
of
B.
We
now show
that
HI
and
H2
are complete graphs. Set
nl
:=
lVII,
n2
:=
1V21
and
n
:=
IV(G)I. Let r denote
the
radius
of
the
Delaunay
polytope
Pc;
r is
given by
relation
(17.2.2). So,
r2
= 2 _ k + 2 =
nl
- 1 +
n2
-
1.
n
nl
n2
Let
rm
denote
the
radius
of
the
Delaunay
polytope
whose I-skeleton
graph
is
the
graph
H
m
,
for m =
1,2.
Then,
r2
= ri + d holds.
We
use
the
following
observation: For each
Delaunay
polytope
P in a
root
lattice, its
radius
r satisfies
2>
IV(P)I-l
r - IV(P)I
with
equality
if
and
only
if
P is a simplex. Therefore,
since
IV(Hm)1 ? n
m
,
for m =
1,2.
But,
from which
we
deduce
that
and,
thus,
Hm
is
the
complete
graph
K
n
= for m =
1,2.
I
Corollary
17.2.4.
Let
G
be
a connected regular graph
on
n nodes with valency
k
and
such
that
Amin(A
G
)
?
-2.
Then, one
of
the following assertions holds.
(i) G is the line graph
of
a bipartite semiregular graph and n =
n~+~2
(k
+ 2),
for
some
nl,
n2
? 1.
(ii) G is the line graph
of
a regular graph
and
n =
T(k
+
2)
for
some
m ? 3.
(iii) G =
Kmx2
and
n = k +
2.
(iv) G is
an
induced subgraph
of
the Gosset graph G
5
6 and n =
2(k
+ 2).
(v) G is
an
induced subgraph
of
the Schliifii graph G
27
and
n =
~(k
+ 2).
(vi) G is an induced subgraph
of
the Clebsch graph
~H(5,
2)
and
n =
~(k
+ 2).

266
Chapter
17.
Hypermetric
Graphs
Proof.
Let
He
denote
the
I-skeleton
graph
of
the
Delaunay
polytope
P
e
associ-
ated
with
the
hypermetric
space
(V(G),
2d
a
).
If
He
is a direct
product,
then
we
have (i) by
Lemma
17.2.3. So
we
now suppose
that
He
is one
of
the
Delaunay
polytope
graphs
from
Figure
14.3.1. We know
that
the
radius
r
of
P
e
satisfies
r2
= 2 -
~
<
2.
•
If
He
=
J(m,
t)
for some t
~
1,
n
~
2t,
then
r2
=
t(:;-t)
< 2 implying
that
t =
1,2,3.
If
He
=
J(m,l)
= K
m
,
then
G =
He
=
Km
is
the
line
graph
of
the
bipartite
semi regular
graph
K1,m; hence, m = n
and
we
have (i).
If
He
=
J(m,2)
=
L(Km),
then
G is a line graph. Since G is regular, one
can
check
that
G is
the
line
graph
of a regular
graph
or
a
bipartite
semiregular
graph.
Since
r2
=
2(:;-2),
we
deduce
that
n =
if(k
+ 2). So,
we
have (i) or
(ii).
If
He
=
J(m,3),
then
m =
6,7,8.
If
He
=
J(6,3),
then
G
is
an
induced
subgraph
of
G
56
and
r2
=
~
= 2 -
~,
yielding n = 2(k + 2), Le.,
we
have (iv).
The
cases m =
7,8
are excluded. Indeed, one
can
check
that
every
subgraph
K
of
J(m,
3)
(m
=
7,8)
such
that
K
is
not
contained
in
J(6,
3)
nor
in
J(n,
2)
and
such
that
no
pair
of
nodes
of
K is
at
distance 3
in
J(m,
3) has
strictly
less
than
m(k+2)
nodes.
9-m
•
If
He
=
Kmx2,
then
we
have (iii).
•
If
He
=
~H(m,
2) for some m
~
4,
then
r2
= if <
2,
implying
that
m =
4,5,6,7.
If
m =
4,
then
He
= K
4X2
and, thus,
we
have (iii).
If
m =
5,
then
r2 =
~
yielding n =
~(k
+ 2)
and,
thus,
we
have (vi).
If
m = 6,
then
r2
=
~
yielding n = 2(k + 2)
and,
thus,
we
have (iv) since
~H(6,
2) is
an
isometric
subgraph
of
G
56
•
The
case m = 7 is excluded (similarly
to
the
exclusion above
of
the
cases
J(7,
3)
and
J(8,
3); indeed, there is no k-regular
subgraph
of
~
H(7,
2)
on
n = 4(k
+2)
nodes which is
not
contained
in
~H(6,
2)
or
J(7,
2)
and
does
not
contain
a
pair
of
vertices
at
distance 3).
•
If
He
= G
56
,
then
we
have (iv) and,
if
He
= G27,
then
we
have (v). I
Remark
17.2.5.
Under
the
assumptions
of
Corollary 17.2.4,
the
only possibili-
ties for
the
I-skeleton
graph
He
ofthe
Delaunay
polytope
P
e
associated
with
the
hypermetric
space
(V(G),2d
a
)
are
He
=
Knl
x K
n2
,
J(m,I),
J(m,2),
J(6,3),
K
mx
2,
!H(5,2), !H(6,2),
G
27
and
G
56
•
In
particular,
if
G is
not
a line
graph
nor
a cocktail-party
graph,
then
He
is one
of
J(6,
3),
~H(5,
2),
~H(6,
2), G
27
or
G
56
• Note
that
the
radius
r
of
the
Delaunay
polytope
P
e
satisfies r2 =
~
for
~H(5,
2),
r2
=
~
for G
27
and
r2
=
~
for
~H(6,
2),
J(6,3)
and
G
56
• I
The
graphs
for which Amin(AG)
~
-2
have
been
intensively
studied
in
the
literature.
Clearly, Amin(AG)
~
-2
for every line
graph
G (indeed,
if
G =
L(H),
then
2I
+ AG =
NT
N is positive semidefinite, where N is
the
node-edge incidence
matrix
of
H).
Moreover, Amin(AG) =
-2
if
G is a cocktail-party graph. More
generally, Amin(AG)
~
-2
for all generalized line graphs.
In
fact, generalized line graphs
constitute
(up
to a finite
number
of
excep-
tions)
the
only connected
graphs
with
Amin(AG)
~
-2.
More precisely,
Cameron,

17.2
Hypermetric
Regular
Graphs
267
Goethals, Seidel
and
Shult
[1976]
show
the
following results:
If
G
is
a con-
nected
graph
on
n > 36 nodes satisfying Amin(Ao)
~
-2,
then
G is a gener-
alized line graph. Moreover, if G is connected regular
with
n >
28
nodes
and
Amin(Ao)
~
-2,
then
G is a line
graph
or a cocktail-party
graph.
This
leads us
to
consider
the
class
LBGS,
consisting
of
the
connected
regular
graphs
with
Amin(Ao)
~
-2
and
which are not line
graphs
nor
cocktail-party
graphs. Bussemaker, Cvetkovic
and
Seidel
[1976]
have completely described
the
graphs
in
LBGS.
The
class
LBGS
consists
of
187 graphs, each
of
them
has
n ::;
28
nodes
and
valency k
::;
16.
The
graphs
in
LBGS
are
partitioned
into three layers
L
1
, L
2
,
L3
depending
on
the
value
of
the
quantity
k~2'
where n
is
the
number
of nodes
and
k
the
valency
of
a
graph
in L
BGS
.
The
layer
L1
(resp. L
2
, L
3
)
consists
of
the
graphs
G E
LBGS
for which
k~2
= 2 (resp.
k~2
=
~,
k~2
=
~).
Our
approach
permits
to shed a new light
on
the
parameter
~
characteriz-
ing each layer
of
LBGS.
Namely,
the
parameter
~
is
nothing
but
the
quantity
2 - r2, where r is
the
radius
of
the
Delaunay
polytope
associated
with
the
hy-
permetric
space
(V(G),2d
o
)
for
any
graph
G E
LBGS.
Therefore, each layer in
LBGS
is characterized by a
quantity
directly derived from the
hypermetricity
of
its graphs.
We
summarize
below several facts
about
the
class L
BGS
and
its
three
layers.
•
The
first layer
L1
consists
of
163
graphs
(the
graphs NNl-163 in Bussemaker,
Cvetkovic
and
Seidel [1976]); it
is
characterized by
k~2
=
2.
For each
graph
G E
LBGs,
the
Delaunay
polytope
Po
associated
with
the
hypermetric
space
(V(G),
U
a
)
has
radius
~
and
its I-skeleton
graph
is
~H(6,
2), J(6,3),
or
G56'
Hence, each
graph
G E
L1
is
an
induced
subgraph
of
G56
and
thus
has
diameter
2
or
3.
Therefore,
the
graphs
of
L1
with
diameter
2 are
hypermetric
with
Delaunay
polytope
graph
~H(6,
2), J(6, 3),
or
G56'
•
The
second layer L2 consists
of
21
graphs
(the
graphs NN164-184 in Busse-
maker, Cvetkovic
and
Seidel [1976]) including
the
Schliifli
graph
G
27
(which
is
N184).
It
is
characterized by
the
value
k~2
=
~.
For each G E L
2
,
the
Delaunay
polytope
P
a
is
221
with
radius
r,
r2
=
~.
Hence, each G E L2 is
an
isometric
subgraph
of
G
27
and
thus
has
diameter
2
and
is
hypermetric.
•
The
third
layer
L3
consists
of
3 graphs;
they
are
the
Clebsch
graph
~H(5,
2)
(N187 in Bussemaker, Cvetkovic
and
Seidel [1976])
and
two of its regular sub-
graphs
(the
graphs
NN185,186).
L2
is
characterized
by
the
value
k~2
=
~.
For
each
graph
G E L
3
, P
a
=
hi5
with
radius
r,
r2
=
~,
with
I-skeleton
graph
~H(5,
2). Therefore, each
graph
of
L3
is
an
isometric
subgraph
of
~H(5,
2)
and
thus
has
diameter
2
and
is
an
iI-graph
with
Delaunay
polytope
graph
~H(5,2).
Properties
of
the
Path
Metric
of
a
Distance-Regular
Graph.
We con-
clude
this
section
with
some results on hypermetric distance-regular graphs. A
graph
G
is
said to
be
distance-regular if
there
exist integers b
m
,
em
(m
>
0)
such
that
for
any
two nodes
i,j
E
V(G)
at
distance
do(i,j)
= m there are exactly
em
nodes
at
distance
1 from i
and
distance m - 1 from
j,
and
there
are b
m
