Deza M.M., Laurent M. Geometry of Cuts and Metrics
Подождите немного. Документ загружается.


238
Chapter
16.
Extreme
Delaunay
Polytopes
a
Hadamard
matrix
A of order n -
2;
the
rows of
this
extended
matrix
provide
n - 2 vectors
of
norm
n - 1
and
pairwise inner
products
1. Placing copies of
them
on
every 5(i) yields
n(n
-
2)
vectors in
jR(;)
with
norms
n - 1
and
inner
products
±1.
I
We now
present
a
general
construction
for
equiangular
sets
of
lines
by
taking
a
suitable
section
of
the
sphere
of
minimal
vectors in
an
integral
lattice.
Let
L
be
a
lattice
with
minimal
norm
t
and
let
Lmin
be
its
set
of
minimal
vectors.
Given a E
L,
a
-#
0,
set
V:=
{u
E Lmin
12u
T
a
= a
2
}. Hence, all u E V lie
on
a
sphere
with
center
~.
By
Lemma
13.2.11,
if
V
-#
0,
then
the
polytope
P
:=
Conv(V)
is
a
Delaunay
polytope.
Moreover, P is
centrally
symmetric.
The
following
properties
can
be
easily checked: V
-#
0 if
and
only
if a =
al
+
a2
for
some
al,a2
E Lmin
and,
then,
al,a2
E
V.
If
V
-#
0,
then
WI
= 1
if
and
only
if
a
2
= 4t.
If
WI
;::
2
then,
for all
u,
v E V such
that
v
-#
u,
a -
u,
we have
(16.1.8)
a
2
-
t T t
--<u
v<-
2 - - 2
(This
follows from
the
fact
that
(u
-
V)2
;::
t
and
(u
+ v - a)2
;::
t.)
This
implies
that
t
S;
a
2
S;
2t
if
WI
;::
3.
Since P is
centrally
symmetric,
we
can
arrange
its vertices
into
pairs
of
antipodal
vertices.
Each
such
pair
determines
a line going
through
~
and
with
direction
2u -
a,
for
u E
V.
Let
£
denote
this
set
of
lines
and
let
V'
:=
{
V2(
u -
~)
I u E
V}
denote
the
set
of
their
directions.
Note
that
U
'2
=
2t-
~
for u
'
E
V',
and
U
'T
v'
= 2u T
v-
~
for u
'
,
v'
E
V'.
Therefore,
if
L is
an
integral
lattice,
then
U
'2
, U
'T
v'
are
integers
with
the
same
parity
as
~.
Note
also
that,
from relation (16.1.8), we have
that
-(t
-
~)
S;
U
'T
v'S;
(t -
~)
for
u
'
,
v'
E V',
v'
-#
u
'
,
-u
'
.
Using
the
above observations, we
obtain
the
following
result
from
Deza
and
Grishukhin
[I995a].
Proposition
16.1.9.
Let
£ denote the set lines determined by the diagonals
of
the
polytope P
=
Conv(V)
(defined
as
above). The following assertions hold.
(i)
If
a
2
= 2t, then the lines in £ are pairwise orthogonal.
(ii) Suppose a
2
=
2t
- 2, t
;::
2 and L is an integral lattice. Then, £ is an equiangular
set
of
lines with common angle arccos(
t~l)
(resp. arccos(O) = V
if
t is even
(resp. odd).
(iii) Suppose a
2
=
2t
- 4, t
;::
4 and L is an integral lattice.
If
t is odd, then £ is
equiangular with common angle arccos(
t~2)
and,
if
t is even, then there are two
possible angles between the lines
of
£,
namely
arccos(t~2)
and arccos(O)
=~.
I
We give
an
illustration
of
the
above
construction
in
the
case (ii) when a
2
=
2t
- 2,
= 2
and
L is a
root
lattice
(see
Deza
and
Grishukhin
[I995a] for details).
If
L is
an
irreducible
root
lattice,
we
indicate
what
is
the
Delaunay
polytope
P
produced
by
the
construction,
the
number
of
lines in
the
equiangular
set
£
of
its diagonals
and
the
dimension
in which £ occurs.
- for L =
An-I,
P =
(3n-l,
1£1
= n
-1,
in dimension n -
1,
- for L =
Dn,
P =
al
x (3n-2,
1£1
= 2(n - 2), in dimension n -
1,
- for L = E
6
,
the
I-skeleton
graph
of
Pis
J(6,3),
1£1
= 10, in dimension 5,
- for L = E
7
,
P =
~H(6,
2),
1£1
= 16, in dimension 6,

16.2
The
SchHifli
and
Gosset Polytopes
239
-
for
L =
Ea,
P = 321>
1£1
=
28,
in
dimension
7.
Note that,
in
dimensions 5 and
6,
the maximum cardinality of an equiangular set of
lines
is
equal to
10
and
16,
respectively;
so
the
two
examples above from
E6
and
E7
are
optimum.
16.2
The
Schliifli
and
Gosset
Polytopes
are
Extreme
In
this
section,
we
show
that
the
SchHifli
polytope
221
and
the
Gosset
polytope
321
are extreme.
The
proof
uses
the
treatment
for
the
notion of
rank
developed
in
Section 15.1.
The
main
steps
of
the
proof
are:
(i)
Find
an
affine basis
E;
so
lEI
= 7 for
221
and
lEI
= 8 for
321
(thus, showing
that
both
221,321
are basic Delaunay polytopes).
(ii) Using
the
affine decomposition of each nonbasic vertex
in
E,
find
the
ex-
plicit description of
the
system
S(E,
d(2))
(it consists of 27 - 7 =
20
equa-
tions for
221
and
of ¥ - 1 =
27
equations for
321).
(iii) Show
that
the
solution set
to
the
system
S(E,
d(2))
has
rank
1.
For this,
we
need
an
explicit description
of
the
polytopes 2
21
,3
21
. We refer,
for instance,
to
Brouwer, Cohen
and
Neumaier [1989], Conway
and
Sloane [1988,
1991] for a detailed account of
the
facts
about
E
6
, E
7
,
E8
mentioned below.
The
lattice
E8
is defined by
1
E8
= {x E
]R8
I x E Z8 U
(2
+ Z)8
and
L
Xi
E 2Z}.
l:'Si:'S8
Let
V8
denote
the
set
of
minimal
vectors of E
8
.
Then
V8 consists
of
•
the
112 vectors
(±1
2
,06)
and
•
the
128 vectors
(±~
8)
that
have
an
even
number
of minus signs.
So,
!V81
= 240
and
v
T
v = 2 for v E V
8
.
The
set V8 lies
on
the
sphere 8
8
with
center °
and
radius
viz.
Let
Vo
=
(1,1,0
6
)
be
a given
minimal
vector.
One
can
check
that
v
T
Vo
0,
±1
for all v E V
8
,
v
=1=
±vo.
The
lattice
E7
is
defined by
Let
H7
denote
the
hyperplane defined by
the
equation
x
T
Vo
=
1;
then,
8
7
8
8
n
H7
is
the
7-dimensional sphere
with
center
~
and
radius
~.
Set
Then,
V
7
consists
of
•
the
12
vectors
(1,0,±1,05),
•
the
12
vectors (0,1,
±1,
0
5
)
and
•
the
32
vectors
(~,
~,
±
~
6
)
with
an
even
number
of minus signs.

240
Chapter
16. Extreme Delaunay Polytopes
So,
1V71
=
56
and
V
7
lies
on
the
sphere 8
7
•
By Lemma 13.2.11,
the
polytope
Conv(V7) is a Delaunay polytope;
it
is known as
the
Gosset polytope
and
is
denoted by 3
21
, Observe
that
the
56
points of
V7
are partitioned into
28
pairs
of
antipodal
points (with respect to
the
sphere Le.,
the
antipode of v is
v·
=
Va
- v). So,
the
polytope
321
is centrally symmetric.
Let
wo
=
(~)8
E V
7
,
so
Wo
(h
h
-t
6
).
One
can
check
that
vTwo = 0,1
for all
v E V
7
, V
i=
Wo
and
v
i=
wo'
Then,
the
lattice
E6
is defined by
Note
that,
if
v·
is
the
antipode of v E
V7,
then
vTwo +
(v'fwo
=
vlwo
= 1
and, thus,
v
T
Wo
1 if
and
only if
(v'fwo
=
O.
Let
H6
denote
the
hyperplane
defined by
the
equation x
T
Wo
1;
then, 8
6
=
87
n
H6
= 8
8
n
H7
n
H6
is
the
6-dimensional sphere
with
center
vot
wq
and
radius
y1.
Set
V6
{x
E V
7
I x
T
Wo
=
I}
and
\16*
{v*
I v E
V6}.
Hence, V
7
=
V6
U
V6*
U {wo,wO}.
The
set
V6
consists of
•
the
6 vectors
(1,0,1,0
5
),
•
the
6 vectors
(0,1,1,0
5
)
and
h
~
(1
1
12
14)
• t e
Iv
vectors
2' 2'
-2
'2
.
Hence,
IVGI
27
and
VG
lies
on
the
sphere 8
6
,
The
polytope Conv(V
6
)
is a
Delaunay polytope (by Lemma 13.2.11).
It
is
known as the Schlafli polytope
and
is
denoted
by
221;
it
is asymmetric.
Remark
16.2.1.
(i)
The
28
lines determined by
the
diagonals of 3
21
form a 7-dimensional
set
of
equiangular lines
with
common angle
arccos(l);
this can be seen directly
or as
an
application of Proposition 16.1.9 (ii).
(ii) For
u,v
E
VG,v
i=
u,uTv
E {0,1}
and
thus d(2)(u,v) = (u
v)2
4
(if u
T
v
0)
or 2
(ifu
T
v = 1). Therefore,
the
27 vertices
of
221
form a
6-dimensional spherical two-distance
set
of
points.
(iii)
The
graph
whose nodes are
the
vertices of
221
and
with edges
the
pairs
(u,
v)
of vertices at
the
smallest distance
d(2)
(u,
v)
=
2,
is called
the
Schliifli
graph
and
is
denoted by G
27
•
The
graph
whose nodes are
the
vertices
of
321
and
with
edges
the
pairs
(u,
v)
of
vertices
with
d(Z)
Cu,
v)
2 is called the
Gosset
graph
and
is denoted by G
56
•
From Proposition 14.3.3,
GZ7
(resp.
G
56
)
is
the
I-skeleton
graph
of
221
(resp. of 32d. I
We now show
that
the polytopes
221
and
321
are extreme.
This
result was
proved in Deza, Grishukhin
and
Laurent
[1992]
and, independently, in
Erdahl
[1992].
Theorem
16.2.2.
The
Schliifli polytope
221
and
the Gosset polytope
321
are
basic
extreme
Delaunay
polytopes.

16.2
The
Schliifli
and
Gosset Polytopes
241
Proof. We denote
the
vectors of
V6
by
Ui
:=
(1,0,
Ii,
0
5
)
,
Vi
:=
(0,1,
Ii,
0
5
)
(where
the
first two coordinates are fixed
and
the
second 1 stays
in
the
(2+i)-th
position) for 1::;: i::;: 6,
and
Uij:=
(~'~'(-~)i'(-~)j,~4)
(where
the
two
-~'s
stay
in
the
(2
+
i)-th
and
(2
+
j)-th
positions) for 1
::;:
i < j
::;:
6.
Setting
t
:=
2,
we
have
d(Ui,Uj)
d(Ui,Vj)
= d(Vi, Vj)
= t for i
=I-
j,
{
t
if i =
j,
= 2t
if
i
=I-
j,
(16.2.3)
{
t
ifi~{k,l},
=d(Vi,Ukl)=
2t
ifiE{k,l},
_{
t
ifl{i,j}n{k,l}I=I,
- 2t
ifl{i,j}n{k,l}I=O.
One
can check
that
the
set
B
6
:= {U12,U24,U34,U35,UI5,U6,V6}
=:
{1,2,3,4,5,6,
7}
is
an
affine basis of E
6
.
The
affine decompositions
of
the
points
of
V6
\ B6 in B6
give
the
following
system
of20
equations in
the
21
variables
d(i,
j)
(1
::;:
i < j
::;:
7)
(the
indices are
taken
modulo 5):
{
d(i,6)
+ d(i + 1,6) -
d(i,i
+
1)
d(i, 7) + d(i + 1,7) -
d(i,i
+
1)
d(i,i
+ 2)
+d(i,i
+ 3) - d(i +
2,i
+ 3)
d(6,7) + L
d(i,j)-
L
(d(i,6)+d(i,7))
i,iE{k:~1,k+2)
iE{k,k+l,k+2}
= 0 for 1
::;
i
::;
5,
= 0
for
1
::;
i
::;
5,
= 0 for 1
::;
i
::;
5,
= 0
for
1
::;
k
::;
5.
The
equalities
of
the
first, second
and
fourth lines correspond
to
the
repre-
sentations
of
Vi,
Ui
and
Uk6
in B
6
, respectively.
The
equalities
of
the
third
line
correspond
to
the
representations of
U45,
U25, U23,
U13
and
U14
in B
6
. (For exam-
ple,
the
equality
d(l,
6)+d(2,
6)-d(l,
2)
= 0 comes from
the
affine decomposition
V5
= U12 +
U34
-
U6
of
V5
in B6. ) One can verify
that
the
solution set
to
the
system
S(B6,
d(2)) described above
is
precisely given by (16.2.3)
and
thus
has
rank
1.
Therefore,
rk(22d
= rk(B6, d(2)) =
1,
showing
that
221
is extreme.
We now
turn
to
the
case
of
3
21
.
The
set B7
:=
B6 U {wo}
is
clearly
an
affine
basis of
E
7
.
Indeed, V
7
=
V6
U
V6*
U {wo, wo},
Vo
=
U12
+
U34
+
U56
-
Wo
and,
for
V E V
6
,
v*
=
Vo
- V = U12 +
U34
+
U56
-
Wo
- V
is
thus
affinely decomposable in
B
7
. Since
w6v
= 1 for all v E B
6
,
we
have
that
d(2)(wO,v) = 2 for v E B
6
.
From
Lemma
15.3.7 (applied
to
P = 3
21
,
PI
= 2
21
, H = H6
and
w =
ub),
we
deduce
that
rk(22d
= rk(321)' implying
that
3
21
is
extreme.
Note
that
the
system
S(B
7
, d(2))
consists of
the
system
S(B6,
d(2))
together
with
the
following seven equations:
{
d(i,8)
+ d(i + 1,8) -
d(i,i
+
1)
d(l,
2)
+
d(l,
3) + d(2, 3) + d(k, 8) - L (d(i, k) + d(i, 8))
i=1,2,3
= 0
for
1
::;
i
::;
5,
= 0
for
k = 6,7.
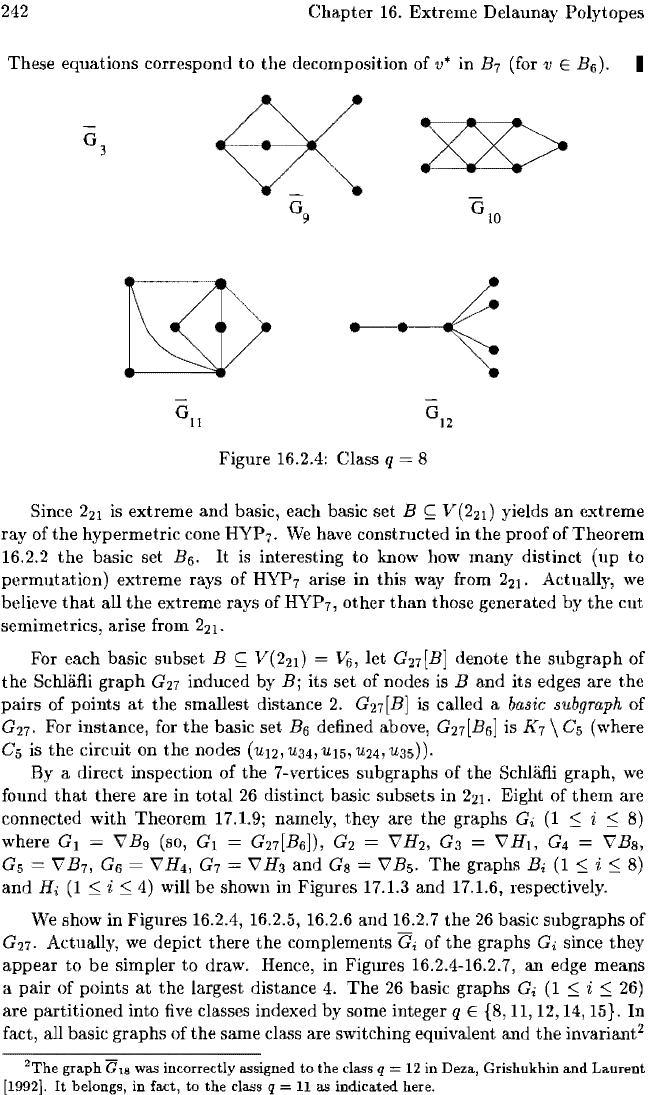
242
Chapter
16. Extreme Delaunay Polytopes
These equations correspond
to
the
decomposition of
v*
in
B7
(for v E Bo). I
Figure 16.2.4: Class q 8
Since
221
is
extreme
and
basic, each basic set B
<;;;
V(22d
yields
an
extreme
ray of
the
hypermetric cone
HYP
7
•
We
have constructed in
the
proof of
Theorem
16.2.2
the
basic set B
6
•
It
is interesting
to
know how
many
distinct
(up
to
permutation)
extreme rays of
HYP
7
arise in this way from 2
21
, Actually,
we
believe
that
all
the
extreme rays of
HYP
7
,
other
than
those generated by
the
cut
semimetrics, arise from 2
21
.
For each basic subset
B
<;;;
V(2
2
1)
=
Ve,
let
G
27
[B]
denote
the
subgraph
of
the
Schliifli
graph
G27
induced by
Bj
its
set
of nodes is B and its are
the
pairs
of points
at
the
smallest distance
2.
G27[B]
is called a
basic
subgraph of
G27.
For instance, for
the
basic set
B6
defined above,
G27[B
6
]
is \ (where
is
the
circuit on
the
nodes
(U12,U34,UI5,U24,U35)).
By
a direct inspection of
the
7-vertices subgraphs of the Schliifli graph,
we
found
that
there
are in
total
26
distinct basic subsets in
221.
Eight of
them
are
connected
with
Theorem
17.1.9; namely, they are the graphs Gi
(1
:s
i
:s
8)
where G
1
'V
B9
(so, G
1
G
27
[B
6
]),
G
2
=
'V
H
2
,
G3
=
'V
HI,
G4
G
5
Go
'V
H
4
, G
7
'V
H3
and
Gs =
'V
B
5
.
The
graphs Bi
(1
:s
i
:s
8)
and
(1
:s
i 4) will
be
shown in Figures 17.1.3 and 17.1.6, respectively.
We show in 16.2.4, 16.2.5, 16.2.6
and
16.2.7
the
26
basic subgraphs of
G27.
Actually,
we
depict there
the
complements G
i
of
the
graphs Gi since
they
appear
to
be
simpler
to
draw. Hence, in Figures 16.2.4-16.2.7,
an
edge means
a
pair
of points
at
the
largest distance
4.
The
26
basic graphs
Gi
(1
:s
i 26)
are partitioned into
five
classes indexed by some integer q E {8, 11, 12, 14, IS}.
In
fact, all basic graphs of
the
same class are switching equivalent
and
the
invariant
2
2The
graph
GIS was incorrectly assigned
to
the
class q = 12
in
Deza,
Grishukhin
and
Laurent
[1992].
It
belongs,
in
fact,
to
the
class q =
11
as
indicated
here.

16.2
The
Schliifli
and
Gosset Polytopes
243
q
of
each switching class is
the
number
of
odd
triples, i.e.,
the
triples of nodes
carrying
an
odd
number
of
edges. (See Deza,
Grishukhin
and
Laurent
[1992]
for
more
details
about
the
occurrence
of
switching here.) Finally,
note
that
one
obtains
at
least
26
distinct
extreme rays for
HYP
g from
the
Gosset
polytope
3
21
.
Indeed, each basic set
of
221
can
be
augmented
to
a basic set
of
3
21
.
We do
not
know
about
the
classification of all
other
basic sets of 3
21
.
Figure 16.2.5: Class q =
11
G
22
Figure 16.2.6: Class q =
12

244
G
23
Chapter
16.
Extreme Delaunay Polytopes
Figure 16.2.7: Class
q =
14
(for
the
first three graphs
\TA
••
\T~Q.
and q =
15
(for the remaining four graphs)
16.3
Extreme
Delaunay
Polytopes
in
the
Leech
Lattice
A24
In
this section,
we
describe two extreme Delaunay polytopes coming from the
Leech lattice
A24i
they
are taken from Deza, Grishukhin
and
Laurent
[1992].
These polytopes have dimension 22,
23
and
they
are constructed by taking two
consecutive suitable sections
of
the sphere
of
minimal vectors
of
A24,
precisely
in
the
same way as the Gosset polytopes
321)
221
were constructed from the
lattice
in
Section 16.2.
We
refer
to
Conway
and
Sloane
[1988]
for
a precise
description
of
the
Leech lattice A
24
;
we
only recall some facts
that
we
need for
our
treatment.
The
Leech
lattice
A24
is a 24-dimensional lattice in
]R24.
For convenience,
the
coordinates
of
the vectors x E
]R24
are indexed by the elements of the set
I {oo, 0,1, .
..
,22}. For i E I, let
ei
denote
the
i-th unit vector in
]R24.
For a
subset 8
of
I,
set
eS
LiES
ei·
Let
1324
denote
the
family
of
blocks
of
the
Steiner system
8(5,8,24)
defined
on
the
set Ii hence,
113241
759. Set
1323
{B
\ {oo} 1 B E
1324
with
00
E B};
so
1323
is
the
family
of
blocks
of
the
Steiner system
8(4,7,23)
defined on
the
set
{O,
1,
...
,
22}
and
113231
253.
In
1323,
there are exactly 176 blocks
that
do
not
contain a given point
and
there are exactly
77
blocks
that
do contain a given
point.

16.4
Extreme
Delaunay Polytopes in
the
Barnes-Wall Lattice
245
The
Leech lattice
A24
is generated by
the
vectors eI 4e
oo
and
2eB for all
blocks
B E 8
24
. Let V denote the set of minimal vectors of A
24
; so, x
T
x =
32
for x E V. (Note
that,
in
the
usual definition, all vectors are scaled by a factor
of
Js
and
the
minimal
norm
is
4;
we
clloose to
omit
this factor in order to make
the
notation
easier.)
The
set V consists of
the
following vectors:
(I) (±42,022) (1104
= 2 x
24
x
23
such vectors),
(II)
(±2
8
,
0
16
),
where
the
positions of
the
nonzero components form a block of
8
24
and
there is
an
even
number
of minus signs
(27
x
759
such vectors),
(III)
(=f3,
±1
23
), where
the
=f3
may be in any position,
but
the
upper
signs are
taken
on
the
coordinates of a codeword of the Golay code C
24
• (Recall
that
the
codewords of C
24
which have exactly 8 nonzero coordinates are
precisely
the
blocks of 8
24
.)
Set
c:=
(5,123)
and
ao:=
(4,4,0
22
);
so
c,ao E A
24
,
Set
By
Lemma
13.2.11, the polytopes
Pn
;=
Conv(Vn), P
22
:=
Conv(V
22
)
48
and
ao
E
V.
are Delaunay polytopes.
The
polytope
P23
is centrally symmetric
and
P
Z
2
is
asymmetric.
In
fact, the set V
22
is a spherical two-distance set (indeed,
the
distances between
the
points of V
22
take
the
two values 32 or 48). Moreover,
the
276 lines defined by
the
276
pairs of antipodal vertices
of
the
polytope P
2
3 are
equiangular (with common angle arccos (
~)).
Theorem
16.3.1.
(i) The polytope is a basic centrally symmetric extreme Delaunay polytope
of
dimension
23
with 552 vertices, hence realizing equality
in
the bound
(16.1.3).
(ii) The polytope is a basic asymmetric extreme Delaunay polytope
of
di-
mension
22
with
275
vertices, hence realizing equality in the bound (16.1.2).
I
16.4
Extreme
Delaunay
Polytopes
in
the
Barnes-
Wall
Lattice
A
16
In
this
section,
we
describe some examples of extreme Delaunay polytopes con-
structed
from the Barnes-Wall lattice
AlB;
they
are taken from Deza, Grishukhin
and
Laurent
[1992].
(See Conway
and
Sloane
[1988]
for a precise description of
A16.)
The
Barnes-Wall lattice
AlB
is a 16-dimensionallattice in
JR16.
Its
set V
of
minimal
vectors consists
of:

246
Chapter
16.
Extreme Delaunay Polytopes
(I) 480 vectors of the form
(±2
2
,
0
14
),
where there are two nonzero components
equal to 2
or
-2,
(II) 3840 vectors of the form (±1
8
,OB),
where the positions
of
the
±l's
form
one of the
30
codewords of weight 8
of
the first order Reed-Muller code
and
there are an even number of minus signs.
Hence,
IVI
= 4320
and
v
T
v = 8 for v E
V.
(Note
that
in
the usual definition,
the
minimal norm is 4
and
all vectors should be scaled by a factor
~;
we
omit
this
factor in order to make the notation easier.)
Cl2
001111
1111
0000
00
CI3
010111 0010
1010
01
CI4
011011 0100
0011
10
CI5
011101
0001
0100
11
CI6
011110 1000
1101
00
C23
100111 0010
0101
10
C24
101011 0100
1100
01
C25
101101
0001
1011
00
C26
• 101110 1000 0010
11
C34
110011 0110
00
C35
110101
0001
01
C3B
110110 1000
10
C45
111001
1000 10
C46
111010
0001
01
C56
111100 0110
00
Figure 16.4.1: Codewords
of
weight 8 in
the
Reed-Muller code
We
show in Figure 16.4.1 a list of
15
codewords
of
weight 8
of
the
first order
Reed-Muller code;
the
other
15
codewords of weight 8 are obtained by taking
their
complements.
Set
a
:=
(2
6
,0
10
) E
Al6
(the six 2's are in
the
first six positions which are
precisely
the
first six positions distinguished in Figure 16.4.1). Let S denote
the sphere
with
center
~
and radius
v'6.
Then, S is
an
empty sphere in
AlB
corresponding
to
a deep hole (i.e., with maximum radius). the polytope
is a Delaunay polytope.
P is centrally symmetric, has dimension
16
and
has
512 vertices. One can check
that
the vertices of P lie in the parallel layers:
xTa
E
{O,
8,12,16, 24}. For a E
:iH:,
let H
a
denote the hyperplane
with
equation
x
T
a = a
and
set
va
:=
V(P)
n H
a
.
Then,
V(P)
= V
O
u
VB
U
Vl2
U V
I6
U V
24
,

16.4
Extreme
Delaunay Polytopes in
the
Barnes-Wall Lattice
with
VO
=
{O},
V24
=
(V0)*
IV
l2
1 = 240.
{a}, V
IB
Moreover, for
0:
8,12,16, the section
p"
P n
H"
= Conv(V")
247
by
the
hyperplane
H"
is a Delaunay polytope of dimension
15
in
the
lattice
AlB
n H".
The
polytopes
p8
and
plB
are asymmetric with 135 vertices,
but
their
sets
of
vertices are not spherical two-distance sets (indeed, there are three
possible distances: 8,12,16 between the vertices).
The
polytope
pl2
is
centrally
symmetric
with
240 vertices,
but
the
120 lines defined by its 120 pairs of
antipodal
vertices are
not
equiangular (there are two possible angles:
arccos(O),arccos(~)).
Note
that
plB
has radius
~
and
that
pl2
has radius
v'6
(>
~).
This
shows
that
plB
does not correspond
to
a deep hole of the lattice
Al6
n
H16.
Finally, set
So,
Q has 2 x
135
+ 2 =
272
vertices
and
its dimension is
16.
Q is a Delaunay
polytope in the lattice
AlB n
{x
I x
T
a = ° (mod 8)}.
The
polytopes
P,
p8,
plB
and
Q can be verified to be basic.
Theorem
16.4.2.
(i) p is a centrally
symmetric
extreme Delaunay polytope
of
dimension 16 with
512 vertices.
(ii)
p8
and
plB
are asymmetric extreme Delaunay polytopes
of
dimension 15,
each having
135 vertices.
(iii)
pl2
is
not
extreme.
(iv) Q is a centrally
symmetric
extreme Delaunay polytope
of
dimension 16 with
272
vertices, hence realizing equality
in
the bound (16.1.3). I
Finally, let us consider
the
section of
the
sphere of minimal vectors by
the
hyperplane H4. In this
way,
one obtains the Delaunay polytope
Qf
Conv(x E
Al6
I x
T
X
= 8 and x
T
a = 4).
Q'
is a IS-dimensional polytope with 1080 vertices. Consider the vertex e
(2,0,
'"
0,
2)
of
Q'.
Then,
the
distances
d(2)
(c,
v) from
the
other vertices v to e
take
the
values 8, 12, 16,
20,
24;
in fact, value 8 (respectively, 12,16,20,24) is
taken
for 119 (respectively, 336, 427,176,21) vertices of
Q'.
Therefore,
the
set of
the
119 vertices
that
are
at
distance 8 from e forms a 14-dimensional asymmetric
Delaunay polytope which realizes equality
in
the
bound (16.1.2). However,
this
polytope is
not
extreme.
On
the
other hand,
the
polytope
Q'
is extreme.
We
summarize in Figure 16.4.3 the results from this section
about
the
De-
launay polytopes constructed from
the
Barnes-Wall lattice AlB.
(The
second
