Deza M.M., Laurent M. Geometry of Cuts and Metrics

15.2

Delaunay

Polytopes

dimension

is m + p +

q.

Note

that

P;:q

does

not

denote a concrete polytope,

but

a class

of

affinely equivalent

repartitioning

polytopes.

We now show

that

the

Delaunay

polytope

associated

with

a facet of

the

hypermetric

cone is a

repartitioning

polytope. Let b E

ZX

with

LiEX

b

i

= 1

and

suppose

that

the

hypermetric

equation:

(15.2.6)

L

b;bjx(i,j)

= a

i,jEX

defines a facet of

HYP(X).

Let d E

HYP(X)

and

suppose

that

d lies in

the

interior of

this

facet, i.e.,

that

(15.2.6) is

the

only

hypermetric

equality satisfied

by

d.

In

particular,

d(i,j)

> a for

distinct

i,j

(else, d would satisfy

2(IXI

-

2)

triangle

equalities).

Proposition

15.2.7.

Let

Pd

be

the

Delaunay

polytope associated with d

lying

in

the

interior

of

the

facet

defined by (15.2.6).

Then,

Pd

is a

repartitioning

polytope

P;:q

where m = I{i I b

i

=

a}l,

p + 1 = I{i I b

i

>

a}1

and

q = I{i I b

i

<

a}l.

Moreover,

Pd

is basic.

Proof. Let

(Vi

liE

X)

denote

the

representation

of

d

on

V(Pd).

From

Proposi-

tion

14.1.5,

the

equality (15.2.6)

is

equivalent to

the

point

(15.2.8)

Va

:=

L biVi

iEX

being

a vertex of

Pd.

From

Proposition

14.1.5 again

and

the

fact

that

(15.2.6)

is

the

only

hypermetric

equality satisfied by d,

we

deduce

that

Va

(j.

{Vi

liE

X},

V(P

d

)

= {Vi

liE

X}

U {va}

and

the

set {Vi

liE

X}

is affinely

independent.

Hence,

Pd

has

IX

I + 1 vertices

and

LVEV(Pd)

bvv

= a is

the

only affine dependency

between

the

vertices of

Pd,

after

setting

b

Vi

:=

b

i

for i E X

and

b

vo

:=

-1.

Set

Va:= {v E

V(P

d

)

I b

v

= a}, V+:= {v E V(Pd) I b

v

> a},

V_

:=

{v E

V(P

d

)

I b

v

< a},

m:=

lVal,p + 1

:=

IV+I

and

q + 1

:=

IV-I.

Then,

PI

:=

Conv(V+ U V_)

is

a

repartitioning

polytope

Pg,q

and

the

polytope

Pd

:=

IIvEVo

Pyrv(P

I

)

is a

repartitioning

polytope

P;:q.

I

As

we

see

in

Example

15.2.10 (iii) below,

there

exist

distinct

hypermetric

facets for which

the

bi's have

the

same

numbers

of positive

and

negative com-

ponents; hence,

they

correspond

to

repartitioning

polytopes

with

the

same

pa-

rameters

p

and

q.

For

this

reason,

we

also denote

the

repartitioning

polytope

associated

with

the

hypermetric

facet (15.2.6) by

P;:q(b).

Note

that

the

matrix

Y-y

characterizing

the

type

of

the

repartitioning

polytope

P~(b)

is

of

the

form

[b/.~bJ

(recall Section 13.3).

We

summarize

in Figure 15.2.9

the

main

facts

we

know

about

the

connections

between faces

of

the

hypermetric cone

and

their

associated Delaunay polytopes.

228

Chapter

15. Delaunay Polytopes:

Rank

and

Hypermetric

Faces

For

the

first two equivalences, see

Examples

14.1.6

and

14.1.7

and,

for

the

last

four equivalences, see, respectively, Propositions 14.1.10, 15.2.7,

Theorem

15.1.8

and

Corollary 15.2.2.

hypermetric

d Delaunay

polytope

Pd

d is a

cut

semimetric

¢=>

Pd

=

Ctl

dE

CUT

n

+

1

¢=>

V(P)

is contained

in

the

set of

vertices of a parallepiped

F(

d)

is a facet

¢=>

Pd

is a

repartitioning

polytope

F(

d)

is

an

extreme

ray

¢=>

Pd

is extreme

F(d) = F(d')

==9

Pd,P

d

'

are affinely equivalent

Figure

15.2.9: Hypermetric faces

and

Delaunay polytopes

Example

15.2.10.

(i) Let (15.2.6)

be

the

triangle equality

x(I,2)

-

x(l,

3)

- x(2,

3)

::;

0,

i.e.,

b

i

= b

2

=

l,b3

=

-1

and

b

i

= ° otherwise.

Then,

(15.2.8) reads

Vo

=

VI

+

V2

-V3

and

V+

=

{VI,

vd,

V_

=

{V3,

vol. Therefore,

the

Delaunay

polytope

associated

with

a triangle facet is

PPI

or, more precisely, PPI(l,

1,

-1),

a

rectangle whose diagonals are

the

segments

[VI,V2]

and

[vo,v~].

(ii)

Let

(15.2.6)

be

a

pentagonal

facet, i.e., b

i

= b

2

=

b3

=

1,

b

4

= b

5

=

-1.

Then,

(15.2.8) reads

Vo

=

VI

+

V2

+

V3

-

V4

-

V5.

Therefore,

the

Delaunay

polytope

associated

with

the

pentagonal facet

is

P~

2 or, more precisely,

P~,2

(1, 1,

1,

-1,

-1),

the

convex hull of two

intersecti~g

triangles.

(iii) Set

b

i

:=

(2,2,2,1,1,1,

-2,

-2, -2, -1,

-1),

b

2

:=

(1,1,1,1,1,1,

-1, -1,

-1).

Then,

(15.2.6) defines a facet for

both

b

i

and

b2.

Hence,

these

two facets are associated

with

repartitioning

polytopes

with

the

same

parameters

p = q = 5 (with, of course,

distinct

affine dependencies (15.2.8)

between

their

vertices). I

Remark

15.2.11.

We group here several observations

on

hypermetric

facets.

(i) For

n

::;

6,

HYP

n

=

CUTn

and

all

the

facets of

HYP

n

are known (see

Section 30.6). Namely, for

n =

3,4,

the

facets of

HYP

n are defined by

the

triangle

inequalities. For n =

5,

they

are defined by

the

triangle inequalities

15.2 Delaunay Polytopes Related to Faces

229

and

the

pentagonal inequalities (6.1.9). For n = 6,

they

are

defined by

the

triangle inequalities,

the

pentagonal

inequalities,

and

the

inequalities

bibjXij

::;

0 for b =

(2,1,1,

-1, -1,

-1)

and

(-2,

-I,

1, 1, 1,

1)

(up

to

permutation

of

the components).

(The

description

in

the

case n = 6

was

obtained

independently by Baranovskii [1971]

and

Avis [1989].)

(ii)

When

n = 7,

the

hypermetric inequality 2:1:5i<j:57 bibjXij

::;

0 for b =

(3,1,1,

I,

-1,

-2,

-2)

defines a facet

of

HYP7,

but

not

of CUT7. Indeed,

there

are precisely

19

linearly independent

cut

semimetrics satisfying

this

hypermetric

inequality

at

equality.

An

additional hypermetric distance

d satisfying equality

can

be

obtained

in

the

following manner: Consider

the

graph

G

g

shown

in

16.2.4 (labeling its nodes as

1,2,3,4,5,6,7

corresponding to degrees

3,2,2,2,5,1,1)

and

set d'j

:=

2 if

ij

is

an

edge

of

Gg, dij

:=

1 if

ij

is

not

an

edge

in

Gg.

This

distance d together

with

19

cut

semimetrics form a set of

20

linearly independent vectors satisfying

the

hypermetric equality; this shows

that

it defines a facet of HYP7.

In

fact, Baranovskii [1995] describes all

the

facets of

the

cone HYP7'

They

are

the

hypermetric facets for CUT7 (see their list

in

Section 30.6) to-

gether

with

the

facets defined by

the

inequalities

2:1::;i<i:57

bibjXij

S;

0, for

b =

(3,1,1,1,-1,-2,

-2),

(-3,1,1,1,1,

2),

(3,-1,-1,-1,1,-2,2),

and

(-3,1,1,

-1,

-1,2,2)

(up

to

permutation).

(iii)

There

is

an

easy way of constructing new hypermetric facets from given

ones, namely, using

the

so-called 'switching' operation.

This

operation

will be described

in

detail

in

Section 26.3;

we

indicate here how

it

acts

on

hypermetric

inequalities. Given b E

zn

and

a subset A C

Vn

{I,

...

,n},

define

the

vector b

A

E

zn

by bf

:=

-bi

if

i E

.4

and

bf

:=

b

i

if i E

Vn

\ A.

If

2::'=1

bi

= 1

and

b(A.) = 0,

then

the

inequality

bfbfXij

S;

0 is

again a hypermetric inequality.

In

fact,

The

hypermetric inequality 2:1

<i<j<n

bibjXij

S;

0 defines a facet

- - A A

of

HYP

n

~

its

switching

2:1:5i<j:5n

b

i

b

j

Xij

S;

0 defines

(a)

a facet of

HYP

n'

See for

an

example

the

facets cited

in

(ii) above. We briefly sketch

the

proof

for assertion (a).

Consider

the

mapping

T5(A) :

~(;)

-----t

~C)

where Y =

TS(A)(X)

is

defined

by

Yij

1

Xij

if

8(A)ij

= 1

and

Yij

:=

Xij

if

8(A)ij

O.

As

HYP

n

is a polyhedral cone,

we

can suppose

that

HYP

n is defined by

the

hypermet-

ric inequalities

2:1

5i

<j:O;n

bibjXij

S;

0 for b E

13,

where

13

is

a finite

subset

of

{bEznl

b

i

I}. Set

13'

:=

{b

A

I

bE

13,

A

~

V

n

}.

For d E

HYP

n

,

set

where

the

minimum is

taken

over all b E

13'

for which 2:1<i<j<n

bibjd;j

>

0,

setting

ad

1 if there is no such

b.

One

can

easily

verify-that

T6(A)(add)

E

230

Chapter

15. Delaunay Polytopes:

Rank

and

Hypermetric

Faces

HYP

n

for all d E HYPn-

We

can now show (a).

If

L19<j:S:n

bibjXij

:::;

0 de-

fines a facet

of

HYP

n

,

then

we

can find

G)

affinely independent vectors d

1

:=

0, d

2

,

.•.

,

d(~)

E

HYP

n

satisfying

the

equality Ll:S:i<j:S:n bibjXij =

O.

Then,

the

vectors

To(A)

(ad,d

i

)

(i =

1,

...

,

G))

are affinely independent

and

satisfy

the

equal-

ity

L19<j:S:n

bfb1

X

ij =

O.

This shows

that

(a) holds.

I

We conclude

this

section

with

an

observation

on

Delaunay

polytopes

with

small

corank. We recall

Problem

13.2.3, which asks

whether

every Delaunay

polytope

is basic.

This

is

indeed

the

case for simplices

and

repartitioning

poly-

topes, i.e., for Delaunay polytopes associated

with

hypermetrics

with

corank 0

and

1.

We

extend

this

fact

to

the

case

of

hypermetrics

with

corank 2

and

3.

Proposition

15.2.12.

Let

P

be

a

k-dimensional

Delaunay polytope

and

let V

be

a generating subset

of

V(P).

If

(I~I)

- rk(V,

d(2))

:::;

3,

then

P

is

basic.

Proof. We show

that

V

is

affinely independent, which implies

that

P

is

basic.

Suppose, for contradiction,

that

LVEC

bvv = 0

is

an

affine dependency

with

G

<:;::

V

and

b

v

1=

0 for v E G. By

Lemma

15.1.4,

the

equations

LVEC

bvx(u,

v) = 0

(for

u E

V)

follow from

the

system

S(V,

d(2)).

One

can

check

that

the

matrix

of

the

subsystem

LVEC

bvx(u, v) = 0 (for u E G)

has

full

rank

IGI.

Since

the

corank

of

(V,

d(2))

is

equal

to

the

rank

of

the

matrix

of

the

system

S(V,

d(2)),

we

deduce

that

corank(V,d(2))

;::::

IGI,

implying

that

IGI

:::;

3. Hence, G =

{Vl,V2,V3}

and,

for instance, V3 belongs to

the

segment

[Vb

V2]'

SO

we have a triangle

with

an

obtuse

angle, yielding a contradiction. I

15.3

Bounds

on

the

Rank

of

Basic

Delaunay

Polytopes

In

this

section,

we

present some

bounds

for

the

rank

of

a basic Delaunay polytope;

they

are

taken

from Deza, Grishukhin

and

Laurent

[1992]. Recall

that

a Delaunay

polytope

P

is

basic if its set

of

vertices

V(P)

contains a basis

of

the

lattice

generated

by

V(P).

Proposition

15.3.1.

Let

P

be

a basic

k-dimensional

Delaunay polytope. Then,

(15.3.2)

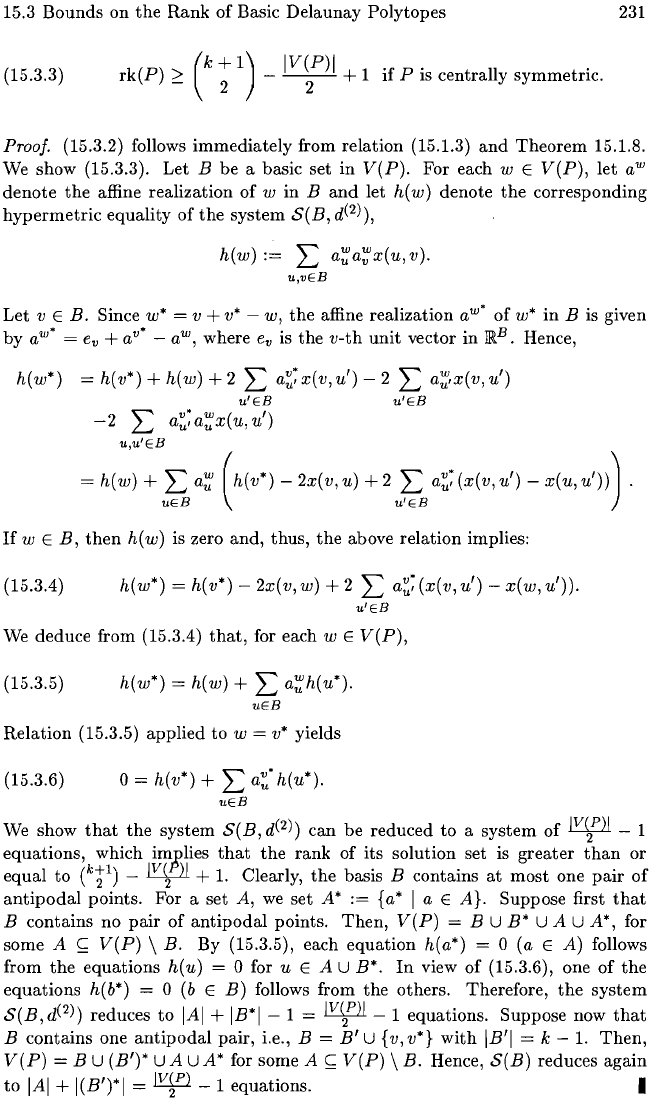
15.3

Bounds

on

the

Rank

of

Basic Delaunay Polytopes

231

(15.3.3)

(

k

+

1)

IV(P)I .

rk(P)

~

2 -

-2-

+ 1

if

P

IS

centrally symmetric.

Proof. (15.3.2) follows

immediately

from relation (15.1.3)

and

Theorem

15.1.8.

We show (15.3.3). Let

B be a basic set in

V(P).

For each w E

V(P),

let a

W

denote

the

affine realization

of

w in B

and

let

h(

w) denote

the

corresponding

hypermetric

equality

of

the

system

S(B,

d(2)),

h(w):=

L a;:'a:x(u, v).

u,vEB

Let v E

B.

Since

w*

= v +

v*

- w,

the

affine realization a

W

'

of

w*

in

B is given

by a

w'

= e

v

+ a

v'

- a

w,

where e

v

is

the

v-th

unit

vector in

~B.

Hence,

h(w*)

=h(v*)+h(w)+2

L

a~;x(v,u')-2

L a;:',x(v,u')

u'EB

-2

L

a~;a~x(u,u')

u,u/EB

= h(w) +

La~

(h(V*)-2X(V,U)+2

L

a~;(x(v,U')-X(U'U')))'

uEB

u'EB

If

wEB,

then

h( w) is zero

and,

thus,

the

above relation implies:

(15.3.4)

h( w*) = h( v*) - 2x( v, w) + 2 L

a~;

(x(v, u') -

x(w,

u')).

u'EB

We deduce from (15.3.4)

that,

for each w E

V(P),

(15.3.5) h(w*) = h(w) + L a'::h(u*).

uEB

Relation (15.3.5) applied

to

w =

v*

yields

(15.3.6)

0=

h(v*) + L

a~'

h(u*).

uEB

We show

that

the

system

S(B,

d(2))

can be reduced

to

a

system

of

IV(}')I - 1

equations, which im;,lies

that

the

rank

of its solution set is

greater

than

or

equal

to

(tl)

-

~

+

1.

Clearly,

the

basis B contains

at

most

one

pair

of

antipodal

points. For a set A,

we

set

A*

:=

{a*

I a E

A}.

Suppose first

that

B contains no

pair

of

antipodal

points.

Then,

V (P) =

BUB

* U A U A

*,

for

some

A

~

V(P)

\

B.

By (15.3.5), each

equation

h(a*) = 0 (a E

A)

follows

from

the

equations h(u) = 0 for u E

AU

B*.

In

view

of

(15.3.6), one

of

the

equations

h(b*) = 0

(b

E

B)

follows from

the

others. Therefore,

the

system

S(B,d(2))

reduces

to

IAI

+ IB*I- 1 = IV(}')I - 1 equations. Suppose now

that

B contains one

antipodal

pair, i.e., B =

B'

U {v, v*}

with

IB'I

= k -

1.

Then,

V(P)

= B U (B')* U

AU

A*

for some A

~

V(P)

\

B.

Hence,

S(B)

reduces again

to

IAI

+ I (B')*I =

IV~P)

- 1 equations. I

232

Chapter

15. Delaunay Polytopes:

Rank

and

Hypermetric

Faces

For example,

the

k-dimensional simplex Ctk

has

k + 1 vertices; hence

both

inequalities in (15.3.2) hold

at

equality for

Ctk.

It

is easy

to

check

that

the

rank

of

the

k-dimensional cross-polytope

(3k

is

(

k+

1)

rk((3k) = 2 - k + 1.

Hence,

(3k

realizes equality

in

the

bound

(15.3.3).

The

will be useful for

computing

the

rank

of Delaunay polytopes.

Lemma

15.3.7.

Let P

be

a basic k-dimensional centrally symmetric Delaunay

polytope and let B

:=

{vo, Vl,

..

.

,vd

be

a basic set in

V(P).

Let H denote

the affine space spanned

by

Bl

:=

{Vl,""

vd

and set P

1

:=

P n

H.

If

P

1

is

an asymmetric Delaunay polytope and

if

there exists w E

V(P)

\ H such that

w

tj.

{vi,

...

,v.n

and w -

Vo

tj.

H,

then

rk(Pl)

=

rk(P)

holds.

Proof.

The

set

Bl

is basic in

V(P

1

)

=

V(P)

n

H.

Hence,

rk(P

1

)

is equal to

the

rank

of

the

solution set to

the

system

S(Bl'

d(2»).

In

order

to

show

that

rk(P)

=

rk(P

1

),

it suffices to check

that

each variable

x(

Vo,

Vi)

(1

:<::;

i

:<::;

k)

can

be expressed

in

terms

of

the

variables

x(

Vi,

Vj)

(1

:<::;

i, j

:<::;

k)

in

the

system

S(B,d(2»).

Let

a,b E ;t;k+l denote

the

affine realizations

ofw,v(j

in

B.

We have

ao

i=

0,1

since w

tj.

Hand

w -

Vo

tj.

H.

Moreover, b

o

i=

-1,

else

the

center

VO~vQ

of P would lie

in

H contradicting

the

fact

that

P

1

is asymmetric. Using

relation

(15.3.4) (applied to V =

Vo

and

w =

Vi),

we

deduce

that

Set

h(v;)

= h(v(j) - 2x(vo,

Vi)

+ 2 L bj(x(vo,Vj) - X(Vi,Vj)).

°sjsk

hi:=

-2

L bjX(Vi,Vj)

lsjsk

for 1

:<::;

i

:<::;

k.

Then,

h(vi)

= h(v(j) - 2x(vo, vi)(b

o

+ 1) + hi + 2 L bjx(vo, Vj).

Osjsk

By

subtracting

the

above relations

with

indices i

and

1,

we

obtain

that

the

equation:

(

a)

hi -

hl

X(VO,Vi)

=

x(vo,vd

+

2(b

o

+

1)

follows from S(B,d(2»). Consider now

the

equation

h(w) =

0,

i.e.,

° = L aiajX(

Vi,

Vj)

+ L aiao

x

(

Vo,

Vi).

lSi<jsk

lSiSk

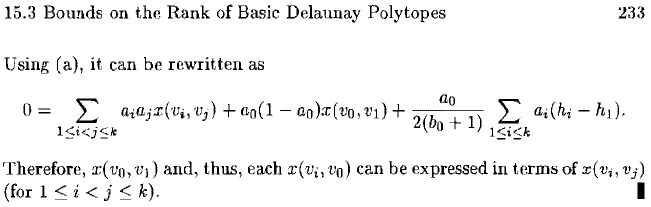
15.3 Bounds on

the

Rank

of Basic Delaunay Polytopes

233

Using (a),

it

can

be rewritten as

Therefore,

x(

Vo,

VI) and, thus, each

x(

Vi,

vol

can

be expressed

in

terms

of

x(

Vi, Vj)

(for 1

:-:;

i < j k). I

M.M. Deza, M. Laurent, Geometry of Cuts and Metrics, Algorithms and Combinatorics 15,

DOI 10.1007/978-3-642-04295-9_16, © Springer-Verlag Berlin Heidelberg 2010

Chapter

16.

Extreme

Delaunay

Polytopes

In

this

chapter,

we

consider extreme Delaunay polytopes, i.e., Delaunay poly-

topes

with

rank

1.

A geometric characterization

of

extreme Delaunay

polytopes

has

been

given

in

Corollary 15.2.4.

Extreme

Delaunay polytopes are

of

particu-

lar

interest

since

they

correspond

to

the

extreme

rays

of

the

hypermetric

cone.

More precisely,

if

d E

HYP

n lies

on

an

extreme ray

of

HYP

n,

then

its associated

Delaunay

polytope

P

d

is

an

extreme

Delaunay

polytope

of

dimension k

S;

n - 1.

Conversely,

if

P is a k-dimensional extreme Delaunay

polytope

then,

for each

generating

subset

V

of

its

set of vertices,

the

hypermetric

space (V,

d(2»)

lies

on

an

extreme

ray

of

the

hypermetric

cone

HYP(V).

Moreover, by

taking

gate

0-

extensions

of

(V,

d(2»),

we

obtain

extreme

rays of

the

cone

HYP

n

for any n

2':

IVI.

In

particular,

if

P is basic,

then

each basic subset

of

V(P)

yields

an

extreme

ray

of

the

hypermetric

cone

HYPk+l

and,

thus,

of

HYP

n

for n

2':

k +

1.

Therefore,

finding all

extreme

rays of

the

hypermetric

cone

HYP

n yields

the

question

of

finding all

extreme

Delaunay polytopes of dimension k

S;

n -

1.

The

only basic

extreme

Delaunay

polytope

of

dimension k

S;

5 is

the

segment

aI,

of

dimension

1.

Indeed, it is known

that

the

only extreme rays of

the

hyper-

metric

cone

HYP

n

(for n

S;

6)

are

the

cut

semimetrics

with

associated Delaunay

polytope

al

(see Deza

[1960]

for n

S;

5

and

Avis [1989] for n =

6;

this

result is

also

implicit

in

Baranovskii [1971, 1973]). Actually, it

is

announced

in

Erdahl

[1992]

that

al

is

the

only

extreme

Delaunay

polytope

of dimension k

S;

5, i.e.,

the

assumption

about

"basic"

can

be

dropped.

For

n

2':

7,

the

hypermetric

cone has

extreme

rays which are

not

generated

by

cut

semimetrics. Indeed,

there

exists a basic

extreme

Delaunay

polytope

of

dimension

6,

namely,

the

Schliifli

polytope

221.

Further

examples of

extreme

De-

launay

polytopes

are presented in Sections 16.2, 16.3

and

16.4.

The

extreme

De-

launay

polytopes

occurring

in

root

lattices

can

be

easily characterized. Namely,

Theorem

16.0.1.

Let P

be

a generating Delaunay polytope in a root lattice.

Then, P

is extreme

if

and only

if

P is the segment

aI,

the Schliifii polytope

221

or the Gosset polytope

321.

Proof. Let L

denote

the

lattice generated by

V(P).

By

assumption,

L is a

root

lattice

and

L is irreducible by

Proposition

15.1.10. Hence, P is one

of

the

Delaunay

polytopes

from

Figure

14.3.1. Therefore, P is equal

to

aI,

221

or

321

since

the

other

polytopes are

not

extreme as

their

Delaunay

polytopes

spaces

236

Chapter

16.

Extreme

Delaunay

Polytopes

I

We

start

the

chapter

with

formulating in Section 16.1 lower

bounds

for

the

number

of

vertices

of

an

extreme

basic

Delaunay

polytope.

It

turns

out

that

they

relate

with

some known

upper

bounds

for sets

of

equiangular

lines. We

refer

to

Deza,

Grishukhin

and

Laurent

[1992]

for details

on

the

topics

treated

in

this

chapter.

16.1

Extreme

Delaunay

Polytopes

and

Equiangular

Sets

of

Lines

In

this

section,

we

present

bounds

on

the

number

of

vertices

of

a basic ex-

treme

Delaunay

polytope

and

we

compare

them

with

some

known

bounds

for

the

cardinality

of

equiangular

sets

of

lines. We also present some

constructions

of

equiangular

sets

of

lines by

taking

sections of

the

sphere

of

minimal

vectors

in

a lattice.

The

follows

immediately

from

Proposition

15.3.1.

Theorem

16.1.1.

Let

P

be

a

k-dimensional

basic

Delaunay

polytope.

If

P is

extreme,

then

(16.1.2)

I

V(P)I

2:

k(k2+

3)

f

i

P is

asymmetric,

(16.1.3) IV(P)I

2:

k(k

+

1)

if

P is centrally

symmetric.

I

Let

Np (k)

denote

the

maximum

number

of

points

in a spherical two-distance

set

of

dimension

k

and

let

Ne(k)

denote

the

maximum

number

of

lines in

an

equiangular

set

of

lines

of

dimension k.

There

is a

striking

analogy

between

the

lower

bounds

(16.1.2), (16.1.3)

and

the

following known

upper

bounds

(16.1.4),

(16.1.5) for

Np(k)

and

Ne(k)

(see Lemmens

and

Seidel [1973]):

(16.1.4)

N

(k)

<

k(k

+

3)

p - 2 '

(16.1.5)

Ne(k)

::::;

k(k:

1)

.

Recall

that

equiangular

sets

of

lines

and

spherical two-distance sets are

in

one-

to-one correspondence.

In

particular,

each

the

two

bounds

(16.1.4), (16.1.5)

can

be

deduced

from

the

other.

The

bound

(16.1.5) was given

by

Gerzon who proved,

furthermore,

that

if

equality

holds

in

(16.1.5),

then

k + 2 =

4,5

or

k + 2 =

q2

for some

odd

integer

q

2:

3 (see

Lemmens

and

Seidel [1973]).

The

first case

of

equality

in (16.1.5) is

Ne =

28

for q = 3, k =

7;

it

is well-known

that

an

equiangular

set of

28

lines

can

be

constructed

from

the

Gosset

polytope

321

(see Section 16.2). Also,

the

set

of

16.1

Extreme

Delaunay

Polytopes

and

Equiangular

Sets of Lines 237

vertices of

the

Schliifli

polytope

221

is a spherical two-distance set

in

~6

, realizing

equality

in

(16.1.4).

The

Nc

= 276 for q = 5, k = 23.

Neumaier

[1987]

has shown how

to

construct

a set of 276

equiangular

lines using

the

Leech

lattice

A24.

In

Section 16.3,

we

shall

see

that

an

extreme

centrally

symmetric

Delaunay

polytope

of

dimension

23

and

with

552 vertices

can

be

constructed

from

this

set

of lines, also

that

a

suitable

section of

it

is

an

extreme

asymmetric

Delaunay

polytope

of

dimension

22

and

with

275 vertices.

The

equality

in

(16.1.5) are

Nc

= 1128 for q =

7,

k = 47,

and

Nc

= 3160 for

q = 9, k = 79;

but

it

is

not

known

whether

such sets of

equiangular

lines exist

in

these two cases.

On

the

other

hand,

we

shall see

in

Section 16.4 some examples

of

extreme

Delaunay

polytopes

realizing equality

in

the

bound

(16.1.2) or (16.1.3),

but

not

arising

from some spherical two-distance set or from some

equiangular

set of

lines. Also,

we

shall have examples of

extreme

Delaunay polytopes

that

do

not

realize

equality

in

the

bound

(16.1.2) or (16.1.3).

Let

Nc(k, a)

denote

the

maximum

number

of

lines in

an

equiangular

set

of

lines of

dimension

k

and

with

common

angle arccos a; so, Nc(k) = maxo: Nc(k, a).

The

following results

can

be

found

in

Lemmens

and

Seidel [1973]:

If

Nc(k, a) >

2k

then

~

is

an

odd

integer. Moreover,

if

k <

;b-,

then

(16.1.6)

When

k =

G)

and

a =

n~l'

the

upper

bound

in

(16.1.6) is

equal

to

n

2

•

For n

even,

Deza

and

Grishukhin

[1996a] propose a

method

for

constructing

a set

of

equiangular

lines

meeting

almost

the

bound.

More precisely,

Proposition

16.1.7.

If

n

==

0 (resp. n

==

2) (modulo 4) and

if

there exists a

Hadamard

matrix

l

of

order n (resp. order n - 2), then one can construct n

2

lines (resp.

n(n

-

2)

lines)

in

dimension

G)

with common angle

arccos(n~l)'

Proof.

In

order

to

construct

N lines

with

common

angle arccos(

n~l)'

it

suffices

to

find N vectors

with

norms

n-1

and

mutual

inner

products

±1.

The

construction

goes as follows.

Consider

first

the

case

when

n

==

0

(mod

4). Let A

be

a

Hadamard

matrix

of

order

n.

Rescale A so

that

its first

column

is

the

all-ones

vector. Deleting

the

first column, we

obtain

a

matrix

whose rows are n vectors

Ul,

...

,Un

in

{±1

}n-l

with

norms

n - 1

and

pairwise

inner

products

-1.

For

each

i = 1,

...

,

n,

consider

the

cut

semimetric

8(

i),

which is a O,l-vector

oflength

G)

with

n - 1

units.

What

we now do is

to

place copies of

the

vectors

Ul,'"

,Un

on

every 8(i) (for i = 1,

...

,n).

In

this

way, we

obtain

N = n

2

vectors

in

~(;)

with

norms

n - 1

and

pairwise

inner

products

±1.

The

reasoning is

similar

in

the

case n

==

2

(mod

4). Namely, we

add

the

all-ones vector as a new

column

to

1 A

Hadamard

matrix

of

order

m is

an

m X m

±l

matrix

A such

that

AT

A =

mI.

Then,

m

==

0

(mod

4)

if

m >

2.

Deza M.M., Laurent M. Geometry of Cuts and Metrics

Подождите немного. Документ загружается.