Deza M.M., Laurent M. Geometry of Cuts and Metrics
Подождите немного. Документ загружается.


14.1
The
Connection
between
Hypermetrics
and
Delaunay
Polytopes
197
Proof.
This
follows
from
the
equality
i,jEX
iEX
stated
in
the
proof
of
Proposition
14.1.2 (ii)
==}
(i).
I
Example
14.1.6.
Consider
the
cut
semimetric
8(S)
for
some
subset
S
<;;:
X.
It
is
obviously
hypermetric.
Its
associated
Delaunay
polytope
is
the
segment
0<1
=
[0,1]
and
a
representation
of
the
hypermetric
space
(X,8(S))
is
i E S
f-+
Vi
:=
1, i
EX
\ S
f-+
Vi
:=
O.
I
Example
14.1.7.
Let
(X,
d)
be
a
semimetric
space.
Then,
d lies
in
the
interior
of
the
hypermetric
cone
HYP(
X)
if
and
only
if
its
associated
Delaunay
polytope
is
the
simplex
0<[X[-1
of
dimension
IXI-l
(since,
by
Proposition
14.1.5, d
satis-
fies
no
nontrivial
hypermetric
equality
if
and
only
if
IV(Pd)1 =
dim(P
d
)
+ 1). I
We
conclude
this
section
with
two
additional
properties
concerning
the
con-
nection
between
hypermetrics
and
Delaunay
polytopes.
A first
observation
is
that,
if
(Y,
d)
is a
subspace
of
the
hypermetric
space
(X,
d),
then
its
associated
Delaunay
polytope
is
embedded
in
the
Delaunay
polytope
associated
to
(X,
d).
Lemma
14.1.8.
Let
P
be
a Delaunay polytope with set
of
vertices
V(P)
and
let X
be
a subset
of
V(P).
Let
Px
denote the Delaunay polytope associated with
the
hypermetric
space
(X,
d(2)). Then,
V(P
x
)
<;;:
V(P)
with equality
if
and only
if
X is a generating subset
of
V(P).
Proof.
Let
Lx
denote
the
sublattice
of
L
generated
by
X
and
let
Ax
denote
the
affine
space
generated
by
X.
Let
S
be
the
circumscribed
sphere
to
P, so S
is
an
empty
sphere
in
L.
The
sphere
Sx
= S n
Ax
is
empty
in
Lx.
Hence,
P
x
=
Conv(Sx
n
Lx)
is a
Delaunay
polytope
and
it
is
the
Delaunay
polytope
associated
with
the
hypermetric
space
(X,
d(2)).
Therefore,
V(P
x
)
=
Sx
n
Lx
is
indeed
contained
in
V(P)
= S n
L.
It
is
easy
to
see
that
V(P
x
)
=
V(P)
if
and
only
if
X
generates
the
lattice
L.
I
In
particular,
every
face
of
a
Delaunay
polytope
is a
Delaunay
polytope.
For
instance,
every
2-dimensional
face
of
a
Delaunay
polytope
is a
rectangle
or
a
triangle
with
no
obtuse
angles.
Corollary
14.1.9.
Let
(X,
d)
be
a hypcrmetric space and (Y, d)
be
a subspace
of
(X,
d), i.e., Y
<;;:
X.
Let
Px
and P
y
denote the Delaunay polytopes associated,
respectively, with
(X,
d)
and (Y, d). Then,
V(P
y )
<;;:
V(P
x
) holds.
I
There
are
some
properties
of
the
hypermetric
space
(X,
d)
which
are
inher-
ited
by
its
associated
Delaunay
polytope.
This
is
the
case for
hypercube
or

198
Chapter
14.
Hypermetrics
and
Delaunay Polytopes
i
I
-embeddability as shown
in
Proposition 14.1.10 below; (i) is proved
in
As-
souad
[1982]
and
(ii) in Deza
and
Grishukhin [1993J. Another such property is
the
notion
of
rank
and
extremality as will
be
seen in Section 15.1.
Proposition
14.1.10.
Let
(X,
d)
be
a hypermetric space and let P
d
be
its asso-
ciated
Delaunay
polytope with
set
of
vertices
V(P
d
).
(i)
Then,
(X,
d) is isometrically iI-embeddable
if
and only
if
P
d
can
be
embed-
ded
in
a parallepiped, i.e., if
(V(P
d
),
d(2)) is isometrically iI-embeddable.
(ii) Moreover,
if
d is rational
7Jalued,
then
(X,
d)
is i)-embeddable
if
and
only
if
Pd
can
be
embedded
in
a hypercube with side length A
for
some
A >
OJ
the
smallest
such A is the
minimum
scale
of
both spaces
(X,
d)
and
(V(Pd),
d(2}).
Proof. (i)
The
set of vertices of a parallepiped endowed with
the
distance
d(2)
is
clearly i)-embeddable. Conversely, suppose
that
(X,
d)
is
ii-embeddable.
Then,
d = L Ah6(8h)
l::;h::;m
where Al,
...
,
Am
> 0
and
8),
...
, 8
m
eX.
Set
e~
:=
,.f5:heh,
where
eh
is
the
h-
th
unit
vector
in
lim, for 1
:::;
h
:::;
m. Let L denote
the
lattice
in
lim generated by
(ei,
...
,
e~).
It
is easy
to
check
that
the
sphere 8 with center c
:=
t
e~
and
radius
II
c I is
empty
in
L.
For i = 1,
...
,
n,
set
h:=
{h E
{1,
...
,m}
liE
8h}'
So, h E Ii
if
and
only
if
i E 8h. Therefore,
d(i,j)
= L
Ah
= L
Ah.
l::h";m,
IShn{i,j}i=l
l";h";m,
hE!;!',.Ij
From this,
we
deduce
that
the
mapping
i E X
I-t
Vi
= L
e~
E lim
hE!;
is a representation of
(X,
d);
indeed,
This
shows
that
the
Delaunay polytope
Pd
associated with
(X,
d)
is embedded
in
the
parallepiped spanned by
e~,
1
:::;
h
:::;
m.
The
assertion (ii) can
be
derived
in
the
same
way.
I

14.2 Polyhedrality of
the
Hypermetric Cone
199
14.2
Polyhedrality
of
the
Hypermetric
Cone
The
hypermetric
cone
HYP
n
+
1
is
defined by infinitely
many
inequalities. Hence,
a
natural
question
is
whether a finite subset of
them
suffices for describing
HYP
n
+
1
or,
in
other
words, whether the cone
HYP
n
+
1
is
polyhedral.
The
answer
is
yes, as
stated
in
the
next theorem proved by Deza, Grishukhin
and
Laurent
[1993].
Theorem
14.2.1.
For any n
;::::
2,
the hypermetric cone
HYP
n
+
1
is polyhedral.
We
present three different proofs for this result. In each of
them,
the
image
e(HYP
n
)
of
the
hypermetric cone
HYP
n
+
1
under
the covariance
mapping
e
is
considered
instead
of
the
cone HYPn+l itself.
The
cone
e(HYP
n
+
1
)
is
shown
to
be polyhedral
in
the
following three ways: either by showing
that
it
has a finite
number
of
faces, or by showing
that
is
can
be decomposed as a finite union of
polyhedral
cones, or by showing
that
it
coincides
with
a larger cone defined by a
finite
subset
of
its inequalities. Recall from (13.1.4)
that
e(HYP
n
+
1
)
is
the
cone
defined by
the
inequalities
(14.2.2)
for all
b E
zn.
The
first
proof
was given by Deza, Grishukhin
and
Laurent [1993].
It
is based
on
the
connection existing between faces of the hypermetric cone
and
types of
Delaunay polytopes
and
it
uses as essential tool
the
fact
that
the
number
of
types
of
Delaunay polytopes
in
any given dimension
is
finite.
The
second
proofrelies
on the fact
that
the
cone
e(HYP
n
+
1
)
can
be decom-
posed as a finite union
of
L-type
domains.
It
uses two results
of
Voronoi;
the
first one concerns
the
finiteness
of
the
number
of types
of
lattices in any given
dimension
and
the
second one concerns properties
of
the
partition
of
the
cone
PSD
n
into
L-type
domains (in particular, the fact
that
each L-type
domain
is
a
polyhedral
cone).
The
third
proof
is
due
to Lovasz
[1994].
It
consists
of
proving directly
that,
among
all
the
inequalities (14.2.2) defining
e(HYPn+l),
only a finite
subset
of
them
is necessary; namely, one shows
that
the inequalities (14.2.2)
with
b
bounded
in
terms
of
n are sufficient for
the
description
of
e(HYP
n
+
1
).
For each
p E
e(HYP
n
+
1
),
the
set
Ep
:=
{x E R
n
I L
XiXjPij
- L
XiPii
=
O}
l:Si,j
:Sn
is
an
ellipsoid (possibly degenerate
with
infinite directions) whose interior is free
of
integral points.
The
key
argument
consists
of
showing
that
if
P lies on
the
boundary
of
the
cone
e(HYP
n
+
1
),
then
Ep
contains
an
integral
point
b which
is
distinct
from 0
and
the
unit vectors
and
is
"short", which means
that
all its

200
Chapter
14.
Hypermetrics
and
Delaunay
Polytopes
components
are
bounded
by a
constant
depending
only
on
n, e.g.,
max
Ibil
::;
n!.
l<t<n
A
better
upper
bound
than
n!
is
given in
Proposition
14.2.4. - -
FIRST
PROOF.
Let
dE
HYP
n
+
l
and
let p
:=
~(d).
The
annullatoT
Ann(p)
of p
is defined as
Ann(p)
= {b E
Zn
I b
=1=
0,
el,""
en
and
L b;bjPij - L
biPii
=
O},
l'Si,j'Sn
where
el,
...
,en
denote
the
unit
vectors
in
Rn. Let F(p)
denote
the
smallest
face of
~(HYPn+l)
containing
p, i.e.,
F(p) =
~(HYPn+l)
n n
Hb,
bEAnn(p)
(
n+l)
where
Hb
denotes
the
hyperplane
in R 2 defined by
the
equation
L bibjPij - L
biPii
=
O.
l'Si,j'Sn
l'Si'Sn
Clearly, showing
that
~(HYP
n+l)
is
polyhedral
amounts
to
showing
that
the
number
of
its
distinct
faces is finite or, equivalently,
that
the
number
of
distinct
annullators
Ann(p)
(for P E
~(HYPn+l))
is finite.
Let
Pd
denote
the
Delaunay
polytope
associated
with
d,
let Ld
be
the
asso-
ciated
lattice
and
let i E X
f-+
Vi
E
V(P
d
)
be
the
representation
of
(X,
d)
on
the
sphere
Sd
with
center c circumscribing
Pd.
We
can
assume
that
Va
= 0;
then,
Ld =
Z(Vl,
...
,vn).
For
vELd,
set
Z(V)
:=
{b E
Zn
I V = L biV;},
l'Si'Sn
Then,
from
Proposition
14.1.5,
(a)
Ann(p)
U
{O,
el,
..
·,
en} = U
Z(v).
vEV(Pd)
Suppose
that
the
polytope
P
d
has
type
,.
Let B
be
a
representative
basis of
the
type,
and
let
Y,
be
the
integer
matrix
characterizing
the
type
" as defined
in
Proposition
13.3.2.
Then,
Qpd
=
Y,MB'
where
Qpd
denotes
the
matrix
whose rows are
the
vectors v E
V(P
d
)
and
MB
denotes
the
matrix
whose rows are
the
vectors
of
B.
Let
Q
denote
the
n x k
matrix
whose rows are
the
vectors
Vi
for 1
::;
i
::;
n. So, Q
may
have
repeated
rows
and
every row
of
Q is a row
of
Q
Pd'
Then,
for some integer
matrix
Y.
Let
Yv
(v
E
V(P
d
))
denote
the
rows of
Y,.
Then
the
rows
of
Yare
the
vectors
YVi
for 1
::;
i
::;
n. Note
that
v = L
biVi
~
Yv
= L biYvi'
l'Si'Sn
l'Si'Sn

14.2
Polyhedrality
of
the
Hypermetric
Cone
201
Therefore,
for each v E
V(P
d
),
Z(V) =
{b
E
zn
I
Yv
= L biYvJ.
1:Si:Sn
Hence, for v E
V(P
d
),
Z(v)
depends
only
on
(Yv,
YVl?
..
'
YvJ.
Using (a),
we
deduce
that
Ann(p) is
entirely
determined
by
the
matrix
Y'Y
and
the
subsystem
(Yvl'
...
,
YV
n
)
of
its
rows.
In
other
words, for each d E
HYP
n+l,
the
annullator
Ann(~(d))
is
completely
determined
by
a
pair
(r,
0), where I is a
type
of
Delaunay
polytopes
in
]Rk
with
k
::;
n,
and
B is a
mapping
from
{I,
...
,n}
to
the
set
of
rows
of
Y'Y.
As
Y'Y
has
IV
(P
d
)
I
::;
2k
rows (by
Proposition
13.2.8),
the
number
of
such
mappings
0 is finite. Moreover,
the
number
of
types
of
Delaunay
polytopes
in
given
dimension
is finite (from
Theorem
13.3.4). Therefore, we
deduce
that
the
number
of
distinct
annullators
Ann(~(d))
(for d E
HYPn+l)
is
finite.
This
shows
that
~(HYPn+l)
is a
polyhedral
cone. I
SECOND
PROOF. We use
the
results
from
Section
13.2.5 concerning
the
parti-
tion
of
the
cone PSD
n
into
L-type
domains. Recall from
relation
(13.1.7)
that
~(HYP
n+l)
is
a
subcone
of
the
cone PSD
n
. More precisely,
the
following holds.
Let
VI,
...
,V
n
E]Rk
with
rank
k (where 1
::;
k::;
n),
set
L:=
Z(Vl,
...
,v
n
),
and
define p E PSD
n
by
setting
Pij =
v[
Vj
for 1
::;
i,
j
::;
n.
Then,
by
the
results
of
Section
14.1,
(b)
P E
~
(HYP
n+
1)
if
and
only
if
L
is
a
lattice
and
VI,
...
,V
n
are all
vertices
of
the
same
Delaunay
polytope
in
the
star
of
L
at
the
origin.
Moreover,
if
P E
~(HYPn+d
then
the
whole
L-type
domain
containing
P is en-
tirely
contained
in
~(HYPn+l).
Hence,
~(HYPn+l)
is a
union
of
L-type
domains.
In
fact,
this
union
is finite.
Indeed,
~(HYPn+l)
contains
only finitely
many
L-
type
domains
whose associated lattices are all z-equivalent (by (b)
and
since,
in
a given
lattice
L,
there
are only finitely
many
ways
of
choosing a set
of
n vectors
VI,
...
,V
n
that
are all vertices
of
the
same
Delaunay
polytope
in
the
star
of
L).
Finally,
the
number
of
distinct
(up
to
z-equivalence) lattices
of
given
dimension
is finite. Therefore,
~(HYPn+l)
is a finite
union
of
L-type
domains.
But,
a
fundamental
property
is
that
each
L-type
domain
is a
polyhedral
cone. Hence,
~(HYPn+l)
is a
polyhedral
cone. I
THIRD PROOF. For P E
~(HYPn+l)'
set
Ep
:=
{x E]Rn I L XiXjPij - L
XiPii
=
O}
l:Si,j:Sn
l:Si:Sn
and
let
Vp
denote
the
kernel
of
the
matrix
(Pij )i,j=l.
If
P is
rational
valued
then
Vp
admits
a basis
composed
of
integral
vectors
and,
therefore, x +
VEEp
for all
x E Ep
and
V E
Vp.
Hence,
if
the
matrix
(Pij) has a nonzero kernel,
then
Ep is a
degenerate
ellipsoid
with
axis
Vp.
As
in
the
first proof, set

202
Chapter
14.
Hypermetrics
and
Delaunay
Polytopes
where
el,
...
,
en
are
the
unit
vectors. By definition of
~(HYPn+1)'
there
are
no
integral
points
lying in
the
interior of
the
region
delimited
by
the
ellipsoid
Ep.
Note
moreover
that
the
vectors 0,
el,
...
,
en
lie on Ep.
The
key
idea
of
the
proof
consists of showing
that,
for each
rational
valued p lying on
the
boundary
of
~(HYPn+1)'
there
exists
bE
Ann(p) which is
"short",
which
means
here
that
max
Ibil
::;
nL
If
we
can
show
this
fact,
then
we
obtain
that
~(HYPn+1)
coincides
l<,<n
~th
the
cone defined by
the
inequalities (14.2.2) for all b
such
that
max
Ibil
::;
n!
l<,<n
(indeed,
the
latter
is a cone containing
~(HYPn+1)
and
whose
bo~~dary
fully
contains
the
boundary
of
~(HYPn+d,
which
means
that
the
two cones coincide).
Assume
that
p is
rational
valued
and
lies
on
the
boundary
of
~(HYPn+1)
and
let
k'
:=
dim(~).
We show
that
(
c)
there
exists
bE
Ann(p)
such
that
max
Ibil
::;
(n - k')L
lS'Sn
Suppose
first
that
k' = 0, i.e.,
that
the
matrix
(Pij) is positive definite.
Then,
Ep
is a (nondegenerate) ellipsoid in
]Rn
and
Ann(p) # 0 as p lies on
the
boundary
of
~(HYPn+1).
Let
b E Ann(p)
and
suppose, e.g.,
that
Ibll,
...
, Ibn-ll
::;
Ibnl.
Let
~
denote
the
n-dimensional
simplex
spanned
by
the
n + 1 vectors
0,
el,
...
,
en-l,
b
(which all lie
on
Ep)
and
let
vol(~)
denote
its
volume.
Then,
vol(~)
=
~II
and
vol(~)::;
1;
n.
the
latter
inequality
holds since Ep is
an
ellipsoid whose interior is free of
integral
points,
which implies
that
vol(~)::;
vol(Conv(ZnnEp))::;
1
(the
last
inequality
is
the
analogue of
the
inequality
vol(P)
::;
det(L)
from
Propo-
sition
13.2.10,
if
P is a Delaunay
polytope
in a
lattice
L).
Therefore,
Ibnl
::;
n!,
i.e., (c) holds.
Suppose
now
that
dim(~)
=
k'
2:
1.
Then,
Ep is a degenerate ellipsoid
with
axis
Vp.
We show
that
Vp
contains
an
integral vector whose
components
are
all
less
than
or
equal
to
(n - k')!. For this, let a
i
,
...
, a
k
'
be
k' linearly
independent
vectors
of
~
n
zn.
For i = 1,
...
,
n,
let
Mi
denote
the
k' x k'
matrix
whose
rows
are
the
vectors
(a~,
...
,a~'_l,a?)
for h =
1,
...
,k',
and
let Di
denote
the
determinant
of
Mi.
Then,
Dl
=
...
=
Dk'-l
= °
and
we
can
suppose
without
loss
of generality
that
D
k
,
#
0.
We
can
also suppose
that
ID
k
'+1I,···,
IDnl
::;
ID
k
,
I.
Set
b:=
(D
l
,
...
,
Dn)T.
For h E {I,
...
, k'}, let
M~
denote
the
(k'
-1)
x (k'
-1)
matrix
whose rows
are
the
vectors (al,
...
,ak'_l)
for r E {1,
...
,k'}
\ {h}
and
set 'Yh:= (_I)h+k'
det(M~).
By
developing
the
determinant
Di
with
respect to its
last
column, we
obtain
that
Di = 1:1ShSk'
'Yha?,
i.e.,
b =
2::
'Yha
h
.
lShSk'

14.2
Polyhedrality
of
the
Hypermetric
Cone
203
This
shows
that
b E
Vp.
Let
9 denote
the
g.c.d. of D
I
,
...
, Dn.
Then,
~b
is
an
integral
vector belonging
to
Vp.
We show
that
~b
satisfies (c), i.e.,
that
IDgk'1
:::::
(n
- k')!.
Set
W
:=
{x
E
ffi.n
I
Xl
=
...
=
Xk'
=
O}.
Then,
ffi.n
=
Vp
+
W.
Let
rr
denote
the
projection
from
ffi.n
on W along
Vp.
So,
if
X = Y + Z is
the
unique
decomposition
of x E
ffi.n
with
y E
Vp,
z E
W,
then
rr(x) = z.
Then,
L
:=
rr(zn)
is a
lattice
in
ffi.
n
-
k
'
which contains
zn-k'
as a sublattice. Moreover, rr(Ep) is a
(nondegenerate)
ellipsoid
in
ffi.
n
-
k
'
which is
empty
in
L,
i.e.,
no
lattice
point
of L
is lying
in
the
interior
of rr(Ep).
Let
~
denote
the
(n
- k')-dimensional
simplex
spanned
by
the
n - k' + 1 vectors
0,
ek'+I,
...
,en, which all belong
to
rr(Ep) n
L.
Then,
vol(~)
= Cn!k')!
and
vol(~)
:::::
det(L) since
the
ellipsoid rr(Ep) is
empty
in
L.
Hence,
_1_
<
(n
_ k')!.
det(L) -
Consider
the
quotient
set
L/Z
n
-
k
'.
Its
cardinality
is equal
to
the
index
of
zn-k'
in
L,
i.e.,
to
detICL). Therefore,
IL/Zn-k'i
=
_1_
<
(n
- k')!.
det(L) -
On
the
other
hand,
as shown below,
IL/Zn-k'i
;:::
~,
which implies
that
the
vector
lb
is
"short".
We show
9
IL/Zn-k'i
;:::
IDnl.
9
For
this,
consider
the
vectors
(Ok'-I,
a,
On-k'), whose
components
are
all
equal
to
0
except
the
k'-th
one equal
to
a,
where a is
an
integer
such
that
0
:::::
a <
IDgk'l.
We show
that
the
projections of these
IDgkd
vectors belong
to
distinct
residue classes
in
the
quotient
set
L/Z
n
-
k
'.
For suppose not.
Let
a,
a'
be
integers
with
0:::::
a <
a'
<
IDgk'1
and
such
that
the
two vectors
(Ok'-I,
a,
On-k'),
(Ok'-I,a',On-k')
belong
to
the
same
class.
Then,
there
exist z E
zn-k'
and
scalars
131,
...
,13k'
E
ffi.
such
that
(Ok'-I,
a'
-
a,
On-k') = L
f3hah
+
(Ok',
z), i.e.,
l:'Oh:'Ok'
{
2:1
<h<k'
f3h
a
?
= 0
2:1~h~k'
f3h
a
Z,
= ao
:=
a'
-
a,
- - h
2:I:'Oh:'Ok,f3hai
=
-Zi
for i =
k'
+ 1,
...
,no
for i = 1,
...
,k' - 1,
The
first k'
equations
of
the
above
system
imply
that
f3h
=
"iDh£>O
for h = 1,
...
,
k'
.
. '
Using
the
last
n - k'
equations
and
the
fact
that
2:1<h<k'
'Yha?
=
bi
=
Di,
we
obtain
that
aoDi
=
-ZiDk',
i.e., - -
Di D
k
,
ao-
=
-Zi-
g 9
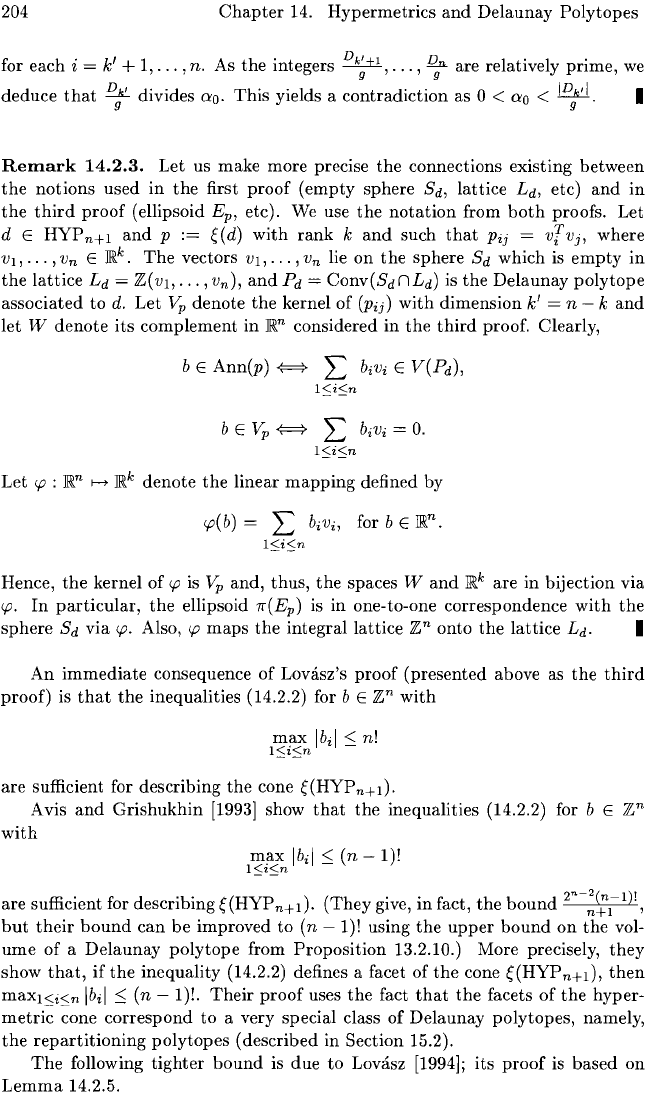
204
Chapter
14.
Hypermetrics
and
Delaunay
Polytopes
£
h
·
k' 1 A
th
. t
Dkl±l
D 1 . 1 .
or eac
~
=
+,
... ,
n.
s e In egers 9 ,
•••
,
=:-
are re atlve y prIme,
we
deduce
that
~
divides ao.
This
yields a
contradiction
as 0 <
ao
<
IDgkil.
I
Remark
14.2.3.
Let
us make more precise
the
connections existing between
the
notions
used
in
the
first
proof
(empty
sphere Sd, lattice L
d
, etc)
and
in
the
third
proof
(ellipsoid E
p
,
etc). We use
the
notation
from
both
proofs. Let
d E
HYPn+l
and
p
:=
~(d)
with
rank
k
and
such
that
Pij =
vr
Vj, where
VI,
...
,V
n
E
Jm.
k
.
The
vectors
VI,
...
,V
n
lie
on
the
sphere Sd which is
empty
in
the
lattice
Ld
=
Z(Vl,""
v
n
),
and
Pd
=
Conv(SdnLd)
is
the
Delaunay
polytope
associated
to
d.
Let
Vp
denote
the
kernel of (Pij)
with
dimension
k' = n - k
and
let W
denote
its
complement
in
Jm.n
considered in
the
third
proof. Clearly,
bE
Ann(p)
~
l:
biVi
E V(Pd),
l:;i:;n
b E
Vp
~
l:
biVi
=
O.
l:;i:;n
Let
<p
:
Jm.n
f-t
Jm.k
denote
the
linear
mapping
defined by
<p(b)
=
l:
biVi,
for b E
Jm.
n
•
l:;i:;n
Hence,
the
kernel of
<p
is
Vp
and,
thus,
the
spaces
Wand
Jm.k
are in bijection via
<p.
In
particular,
the
ellipsoid 7r(Ep) is in one-to-one correspondence
with
the
sphere
Sd
via
<p.
Also,
<p
maps
the
integral lattice
zn
onto
the
lattice
L
d
. I
An
immediate
consequence of Lovasz's
proof
(presented
above as
the
third
proof)
is
that
the
inequalities (14.2.2) for b E
zn
with
max
Ibil
<
n!
I:;i:;n -
are
sufficient for describing
the
cone
~(HYP
n+I).
Avis
and
Grishukhin
[1993]
show
that
the
inequalities (14.2.2) for b E
zn
with
max
Ibil
:s;
(n - I)!
I:;,:;n
are sufficient for describing
~
(HYP
n+I).
(They
give,
in
fact,
the
bound
2n-:~I_
Ill,
but
their
bound
can
be
improved
to
(n - I)! using
the
upper
bound
on
the
vol-
ume
of a
Delaunay
polytope
from
Proposition
13.2.10.) More precisely,
they
show
that,
if
the
inequality (14.2.2) defines a facet of
the
cone
~(HYPn+l)'
then
maxI:;i:;n
Ibil
:s;
(n - I)!.
Their
proof
uses
the
fact
that
the
facets
of
the
hyper-
metric
cone
correspond
to
a very special class of
Delaunay
polytopes, namely,
the
repartitioning
polytopes
(described in Section 15.2).
The
following
tighter
bound
is
due
to
Lovasz [1994];
its
proof
is
based
on
Lemma
14.2.5.

14.2
Polyhedrality
of
the
Hypermetric
Cone
205
Proposition
14.2.4.
The
cone
e(HYP
n
+
l
)
is defined by the inequalities (14.2.2)
for
b E
;;zn
with
2
n
max
Ibil
<
-2-n!.
l~i~n
-
(;:)
Lemma
14.2.5.
Let
E
be
an
ellipsoid
in
lPl.
n
and
let L
be
an
n-dimensional
lattice
in
lPl.
n
.
Suppose
that
E is
empty
in
L,
i. e.,
that
there are
no
lattice
points
lying
in
the
interior
of
the region
delimited
by
E.
Let
Xo
= 0,
Xl,
...
,X
n
be
affinely
independent
points
of
E n L
and
let ~
denote
the
simplex
they
span.
Then,
2
n
vol(~)
S
e:l
det(L).
Proof.
Consider
the
difference
body
~-~:=
{x-y
I
x,y
E
~}.
It
is a
centrally
symmetric
convex
body
around
the
origin
and
one
can
check
that
the
only
lattice
point
lying
in
the
interior
of
~ - ~ is
the
origin. Hence, by Minkowski's
theorem
(see, e.g., Siegel [1989]),
vol(~
-~)
S 2
n
det(L).
On
the
other
hand,
it
is shown in Rogers
and
Shephard
[1957]
that
vol(~
-
~)
=
C:)
vol(~).
This
yields
the
result.
Proof
of
Proposition
14.2.4.
Let
us now call a vector b
"short"
if
2
n
Ibil
S
e:l
n!
I
holds for all 1
SiS
n. Using
the
bound
on
the
volume
of
a
simplex
from
Lemma
14.2.5,
the
third
proof
of
Theorem
14.2.1
can
be
adapted
so as
to
show
the
existence
of
a
short
vector
in
Ann(p)
for each p lying
on
the
boundary
of
e(HYPn+l).
(One
also uses
the
fact
that
2k
2
n
-k'<-n'
e;l
. -
e:l
.
for
all
1 S k S n.)
I
Remark
14.2.6.
From
Proposition
14.2.4, a (rough)
upper
bound
on
the
num-
ber
of
facets
of
the
cone
e(HYPn+l)
(or
of
the
hypermetric
cone HYPn+l) is
given by
(2Bn + l)n,
where
2nn!
E
n
:=
e:l-·
Therefore,
the
problem
of
testing
whether
a given
distance
d is
hypermetric
is
in
co-NP.
It
is
not
known
whether
testing
hypermetricity
is
NP-hard.
But
the
following
complexity
results
are proved by Avis
and
Grishukhin
[1993];
they
will
be
treated
in
detail
in
Section 28.3.

206
Chapter
14.
Hypermetrics
and
Delaunay
Polytopes
(i) Given
an
integral
distance
d
and
an
integer
m,
does d satisfy all (2m + 1)-
gonal
hypermetric
inequalities?
This
problem
is co-NP-complete.
(ii) Given
an
integral
distance
d.
Is d
hypermetric
?
If
not, give
the
smallest
k
such
that
d violates a
(2k+
1)-gonal inequality.
This
problem
is
NP-hard.
I
14.3
Delaunay
Polytopes
in
Root
Lattices
In
this
section,
we
group several results
on
Delaunay
polytopes
in
root
lattices.
First,
we recall
the
description of
the
irreducible
root
lattices
and
of
their
Delau-
nay
polytopes.
We show
that,
if
P is a
Delaunay
polytope
in
a
root
lattice,
then
its I-skeleton
graph
is completely
determined
by
the
metric
structure
of P (see
Proposition
14.3.3).
Then,
we
see
that
Delaunay
polytopes
in
root
lattices arise
in
a
natural
way from
hypermetric
spaces
that
are connected
and
strongly
even
(see
Proposition
14.3.5). As a consequence,
we
obtain
a
characterization
of
the
connected
strongly
even distance spaces
that
are
hypermetric,
or isometrically
f
1
-embeddable
(see
Theorems
14.3.6
and
14.3.7).
Let
P
be
a
Delaunay
polytope
which is generating in a
root
lattice
L.
If
L is
reducible,
then
L =
LIEBL2
where
Ll
and
L2
are
root
lattices. Hence, P = PI
XP2
where Pi is a
Delaunay
polytope
in
Li,
for i =
1,2.
Therefore,
it
suffices to
describe
the
Delaunay
polytopes
that
are
generating
in
some irreducible
root
lattice.
The
irreducible
root
lattices have
been
classified
by
Witt
(see, for instance,
Brouwer,
Cohen
and
Neumaier
[1989]).
They
are
An (n
~
0), Dn (n
~
4),
and
En (n =
6,7,8).
We recall
their
description below;
we
will consider
in
more
detail
the
lattices
E
6
,
E7
and
Es
in
Section 16.2.
For
each
of
the
lattices An, Dn
and
En,
we
recall some
information
about
its
roots
(i.e.,
its
minimal
vectors)
and
about
its
empty
spheres (i.e., its holes).
For
more
details
we
refer, for instance, to Brouwer,
Cohen
and
Neumaier
[1989]'
Conway
and
Sloane [1988, 1991].
Case
of
An,
n
~
O.
• An =
{x
E
zn+l
I
LO::;i::;n
Xi
=
O}.
•
The
roots
of
An
are
the
n(
n +
1)
vectors
ei
- ej, 0
::;
i
of-
j
::;
n, where
ei
denote
the
i-th
unit
vector in lffi.n+l.
•
There
are
l
~
J
types
of
empty
spheres
in
An.
Their
centers
are
a a
e
a
=
(--,
...
,--;
n+l n+l
n+l-a
n+l
n + 1 -
a)
n+l
'
where
n~1
is
repeated
n + 1 - a
times
and
-
nt!la
is
repeated
a times,
with
corresponding
radius
ra
=
Ja(n::;a),
for 1
::;
a
::;
l
~
J.
The
case a = l
~
J
corresponds
to
a deep hole, i.e., a hole
with
maximum
radius.
