Desurvire E. Classical and Quantum Information Theory: An Introduction for the Telecom Scientist

Подождите немного. Документ загружается.

3.4 R

enyi’s fake coin 47

A B C

A = B select C

A < B select A

A > B select B

Step 1

Step 2

A B C

A = B select C

A < B select A

A > B select B

A = B select C

A < B select A

A > B select B

A B C

Step 3

Split

into

Split

into

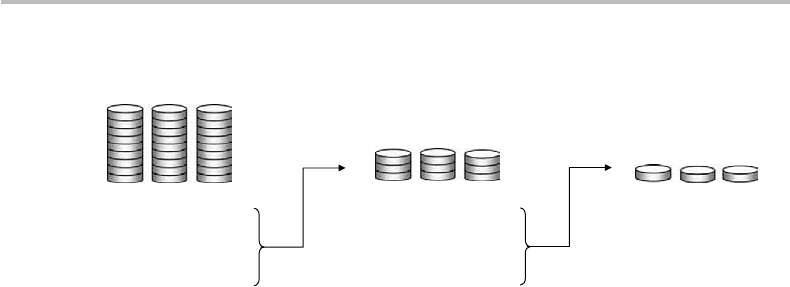
Figure 3.1 Solution of R

enyi’s fake-coin problem: the 27 coins are split into three groups (A, B,

C). The scale ﬁrst compares weights of groups (A, B), which identiﬁes the group X = A, B, or C

containing the fake (lighter) coin. The same process is repeated with the selected group, X being

split into three groups of three coins (step 2), and three groups of one coin (step 3). The ﬁnal

selection is the fake coin.

There exists at least one other way to solve R

enyi’s fake-coin determination problem,

which to the best of my knowledge I believe is original.

The solution consists in making

the three measurements only using groups of nine coins. The idea is to assign to each

coin a position in space, forming a 3 × 3 coin cube, as illustrated in Fig. 3.2.

The coins are thus identiﬁed or labeled with a coefﬁcient c

ijk

, where each of the indices

i, j, k indicates a plane to which the coin belongs (coin c

111

is located at bottom-left

on the front side and coin c

333

is located at top-right on the back side). To describe the

measurement algorithm, one needs to deﬁne nine groups corresponding to all possible

planes. For the planes deﬁned by index i = const., the three groups are:

i=1

= (c

111

, c

112

, c

113

, c

121

, c

122

, c

123

, c

131

, c

132

, c

133

) ≡



1 jk



i=2

= (c

211

, c

212

, c

213

, c

221

, c

222

, c

223

, c

231

, c

232

, c

233

) ≡



2 jk



(3.10)

i=3

= (c

311

, c

312

, c

313

, c

321

, c

322

, c

323

, c

331

, c

332

, c

333

) ≡



3 jk



The other deﬁnitions concerning planes j = const. and k = const. are straightforward.

By convention, we mark with an asterisk any group containing the fake coin. If we put

then P

i=1

and P

i=2

on the scale (step 1), we get three possible measurement outcomes

(the signs meaning group weights being equal, lower, or greater):

i=1

= P

i=2

→ P

∗

i=3

i=1

< P

i=2

→ P

∗

i=1

(3.11)

i=1

> P

i=2

→ P

∗

i=2

We then proceed with step two, taking, for instance, P

j=1

and P

j=2

, which yields either

As proposed in 2004 by J.-P. Blondel of Alcatel (private discussion), which I have reformulated here in

algorithmic form.

48 Measuring information

111

333

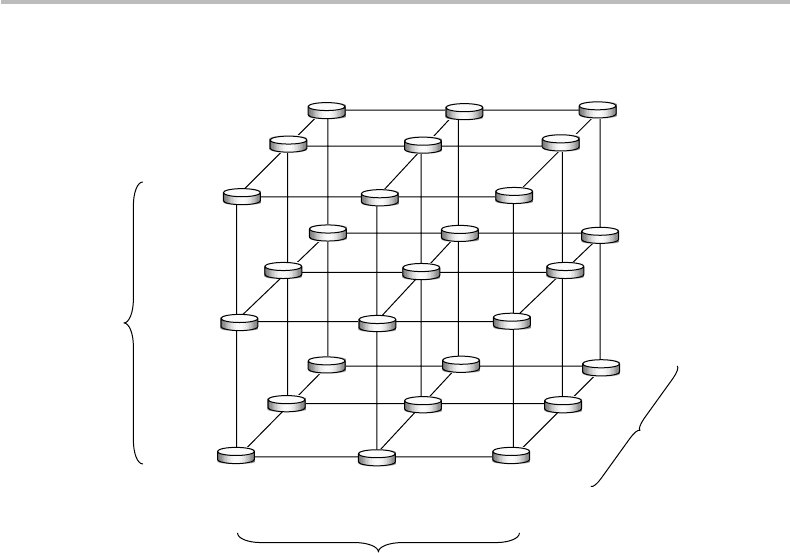
Figure 3.2 Alternative solution of R

enyi’s fake-coin problem: each of the 27 coins is assigned a

coefﬁcient c

ijk

, corresponding to its position within intersecting planes (i, j, k = 1, 2, 3) forming

a3× 3 cube. The coefﬁcients c

111

and c

333

, corresponding to the coins located in

front-bottom-left and back-top-right sides (respectively) are explicitly shown.

of the outcomes:

j=1

= P

j=2

→ P

∗

j=3

j=1

< P

j=2

→ P

∗

j=1

(3.12)

j=1

> P

j=2

→ P

∗

j=2

We then ﬁnally proceed with step three, taking, for instance, P

k=1

and P

k=2

, which yields

either of the outcomes:

k=1

= P

k=2

→ P

∗

k=3

k=1

< P

k=2

→ P

∗

k=1

(3.13)

k=1

> P

k=2

→ P

∗

k=2

We observe that the three operations lead one to identify three different marked groups.

For instance, assume that the three marked groups are P

∗

i=3

, P

∗

j=1

, P

∗

k=2

. This immedi-

ately tells us that the fake-coin coefﬁcient c

∗

ijk

is of the form c

3 jk

and c

i1k

and c

ij2

,or

in mathematical notation, using the Kronecker symbol,

∗

ijk

= c

ijk

≡ c

312

By deﬁnition, δ

= δ

= 1fori = j and δ

= 0 otherwise.

3.5 Exercises 49

In ensemble-theory language, this solution is given by the ensemble intersection

∗

ijk

={P

∗

i=3

∩ P

∗

j=1

∩ P

∗

k=2

}. Note that this solution can be generalized with N = 3

coins ( p ≥ 3), where p is the dimension of a hyper-cube with three coins per side.

The alternative solution to the R

enyi fake-coin problem does not seem too practical

to implement physically, considering the difﬁculty in individually labeling the coins,

and the hassle of regrouping them successively into the proposed arrangements. (Does

it really save time and simplify the experiment?) It is yet interesting to note that the

problem accepts more than one mathematically optimal solution. The interest of the

hyper-cube algorithm is its capacity for handling problems of the type N = m

, where

both m and p can have arbitrary large sizes and the measuring device is m-ary (or gives

m possible outcomes). While computers can routinely solve the issue in the general

case, we can observe that the information measure provides a hunch of the minimum

computing operations, and eventually boils down to greater speed and time savings.

3.5 Exercises

3.1 (B): Picking a single card out a 32-card deck, what is the information on the

outcome?

3.2 (B): Summing up the spots of a two-dice roll, how many message bits are required

to provide the information on any possible outcome?

3.3 (B): A strand of DNA has four possible nucleotides, named A, T, C, and G. Assume

that for a given insect species, the probabilities of having each nucleotide in a

sequence of eight nucleotides are: p(A) = 1/4, p(T ) = 1/16, p(C) = 5/16, and

p(G) = 3/8. What is the information associated with each nucleotide within the

sequence (according to the information-theory deﬁnition)?

3.4 (M): Two cards are simultaneously picked up from a 32-card deck and placed face

down on a table. What is the information related to any of the events:

(a) One of the two cards is the Queen of Hearts?

(b) One of the two cards is the King of Hearts?

(d) Knowing that one of the cards is the Queen of Hearts, the second is the King

of Hearts?

Conclusions?

3.5 (T): You must guess an integer number between 1 and 64, by asking as many

questions as you want, which are answered by YES or NO. What is the minimal

number of questions required to guess the number with 100% certainty? Provide

an example of such a minimal list of questions.

4 Entropy

The concept of entropy is central to information theory (IT). The name, of Greek origin

(entropia, tropos), means turning point or transformation. It was ﬁrst coined in 1864 by

the physicist R. Clausius, who postulated the second law of thermodynamics.

Among

other implications, this law establishes the impossibility of perpetual motion, and also

that the entropy of a thermally isolated system (such as our Universe) can only increase.

Because of its universal implications and its conceptual subtlety, the word entropy has

always been enshrouded in some mystery, even, as today, to large and educated audiences.

The subsequent works of L. Boltzmann, which set the grounds of statistical mechan-

ics, made it possible to provide further clariﬁcations of the deﬁnition of entropy, as

a natural measure of disorder. The precursors and founders of the later information

theory (L. Szil

ard, H. Nyquist, R. Hartley, J. von Neumann, C. Shannon, E. Jaynes, and

L. Brillouin) drew as many parallels between the measure of information (the uncer-

tainty in communication-source messages) and physical entropy (the disorder or chaos

within material systems). Comparing information with disorder is not at all intuitive.

This is because information (as we conceive it) is pretty much the conceptual opposite

of disorder! Even more striking is the fact that the respective formulations for entropy

that have been successively made in physics and IT happen to match exactly. A legend

has it that Shannon chose the word “entropy” from the following advice of his colleague

von Neumann: “Call it entropy. No one knows what entropy is, so if you call it that you

will win any argument.”

This chapter will give us the opportunity to familiarize ourselves with the concept of

entropy and its multiple variants. So as not to miss the nice parallel with physics, we

will start ﬁrst with Boltzmann’s precursor deﬁnition, then move to Shannon’s deﬁnition,

and develop the concept from there.

4.1 From Boltzmann to Shannon

The derivation of physical entropy is based on Boltzmann’s work on statistical mechanics.

Put simply, statistical mechanics is the study of physical systems made of large groups of

This choice could also be attributed to the phonetic similarity with the German Energie (energy, or energia

in Greek), so the word can also be interpreted as “energy turning point” or “point of energy transformation.”

For a basic deﬁnition of the second law of thermodynamics, see, for instance, http://en.wikipedia.org/

wiki/Entropy.

4.1 From Boltzmann to Shannon 51

Energy

Number of particles

. . .

−1

= 2

= 4

= 3

= 8

−1

= 1

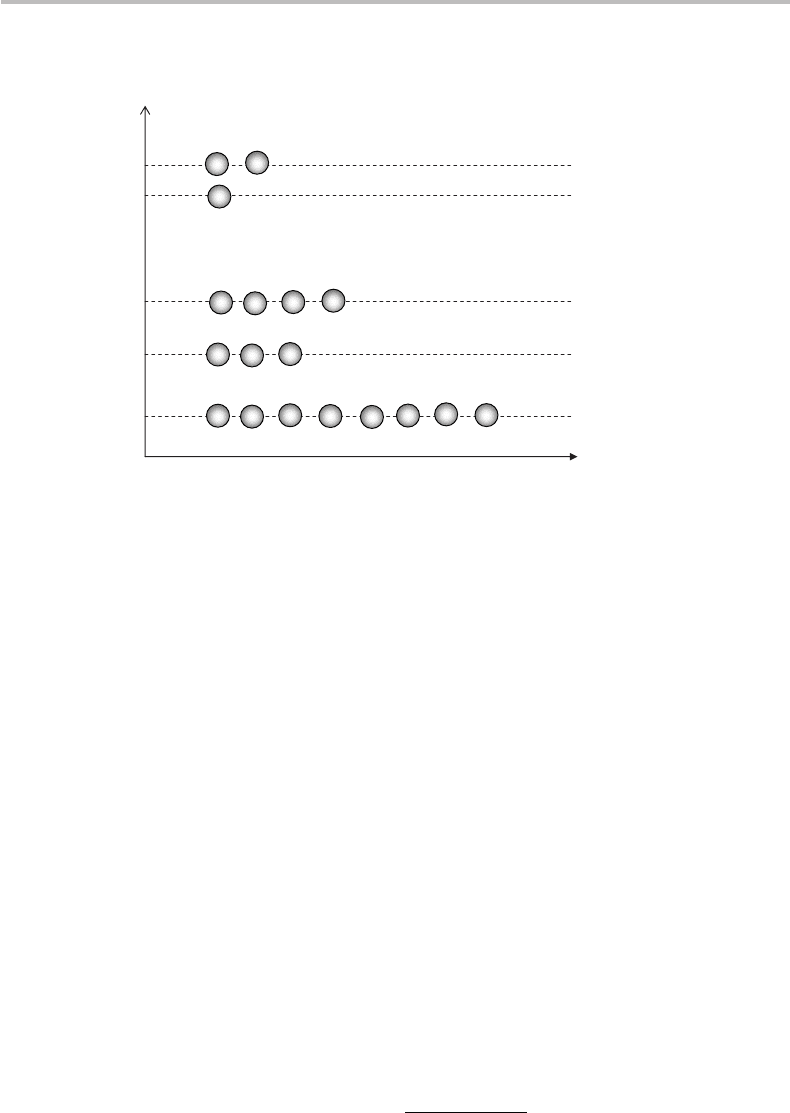
Figure 4.1 Energy-level diagram showing how a set of N identical particles in a physical

macrosystem can be distributed to occupy, by subsets of number N

, different microstates of

energy E

(i = 1 ...m).

particles, for which it is possible to assign both microscopic (individual) and macroscopic

(collective) properties.

Consider a macroscopic physical system, which we refer to for short as a macrosystem.

Assume that it is made of N particles. Each individual particle is allowed to occupy

one out of m possible microscopic states, or microstates,

which are characterized by

an energy E

(i = 1 ...m), as illustrated in Fig. 4.1. Calling N

the number of particles

occupying, or “populating,” the microstate of energy E

, the total number of particles in

the macroscopic system is

N =



i=1

, (4.1)

and the total macrosystem energy is

E =



i=1

. (4.2)

Now let’s perform some combinatorics. We have N particles each with m possible energy

states, with each state having a population N

. The number of ways W to arrange the N

particles into these m boxes of populations N

is given by:

W =

N !

! ...N

(4.3)

A microscopic state, or microstate, is deﬁned by a unique position to be occupied by a particle at atomic

scale, out of several possibilities, namely, constituting a discrete set of energy levels.

52 Entropy

(see Appendix A for a detailed demonstration). When the number of particles N is large,

we obtain the following limit (Appendix A):

H = lim

N →∞

log W

=−



i=1

log p

, (4.4)

where p

= N

/N represents the probability of ﬁnding the particle in the microstate

of energy E

. As formulated, the limit H can thus be interpreted as representing the

average value (or “expectation value” or “statistical mean”) of the quantity −log p

namely, H =−log p. This result became the Boltzmann theorem, whose author called

H “entropy.”

Now let us move to Shannon’s deﬁnition of entropy. In his landmark paper,

Shannon seeks for an improved and comprehensive deﬁnition of information measure,

which he called H . In the following, I summarize the essential steps of the demonstration

leading to Shannon’s deﬁnition.

Assuming a random source with an event space, X, comprising N elements or sym-

bols with probabilities p

(i = 1 ...N ), the unknown function H should meet three

conditions:

(1) H = H ( p

, p

,..., p

) is a continuous function of the probability set p

;

(2) If all probabilities were equal (namely, p

= 1/N ), the function H should be

monotonously increasing with N ;

(3) If any occurrence breaks down into two successive possibilities, the original H

should break down into a weighed sum of the corresponding individual values of

Shannon’s formal demonstration (see Appendix B) shows that the unique function sat-

isfying the three requirements (1)–(3) is the following:

H =−K



i=1

log p

, (4.5)

where K is an arbitrary positive constant, which we can set to K = 1, since the logarithm

deﬁnition applies to any choice of base (K = log

x/ log

x with p = q being positive

real numbers). It is clear that an equivalent notation of Eq. (4.5) is

H(X ) =−



x∈X

p(x)logp(x) ≡



x∈X

p(x)I (x), (4.6)

where x is a symbol from the source X and I (x) is the associated information measure

(as deﬁned in Chapter 3).

C. E. Shannon, A mathematical theory of communication. Bell Syst. Tech. J., 27 (1948), 379–423, 623–56.

This paper can be freely downloaded from http://cm.bell-labs.com/cm/ms/what/shannonday/paper.html.

Based on the fact that equally likely occurrences provide more choice, then higher uncertainty.

Say there initially exist two equiprobable events (a, b) with p(a) = p(b) = 1/2, so H is the function

H(1/2, 1/2); assume next that event (b) corresponds to two possibilities of probabilities 1/3and2/3,

respectively. According to requirement (3), we should have H = H(1/2, 1/2) +(1/2)H(1/3, 2/3) with the

coefﬁcient 1/2 in the second right-hand-side term being justiﬁed by the fact that the event (b) occurs only

half of the time, on average.

4.2 Entropy in dice 53

The function H , which Shannon called entropy, is seen to be formally identical to

the function of entropy deﬁned by Boltzmann. However, we should note that Shannon’s

entropy is not an asymptotic limit. Rather, it is exactly deﬁned for any source having a

ﬁnite number of symbols N .

We observe then from the deﬁnition that Shannon’s entropy is the average value of the

quantity I (x) =−log p(x), namely, H =I =−log p, where I (x)istheinformation

measure associated with a symbol x of probability p(x). The entropy of a source is,

therefore, the average amount of information per source symbol, which we may also call

the source information.

If all symbols are equiprobable (p(x) = 1/N ), the source entropy is given by

H =−



x∈X

p(x)log p(x) =−



i=1

log

≡ log N, (4.7)

which is equal to the information I = log N of all individual symbols. We will have

several occasions in the future to use such a property.

What is the unit of entropy? Were we to choose the natural logarithm, the unit of H

would be nat/symbol. However, as seen in Chapter 3, it is more sensible to use the base-2

logarithm, which gives entropy the unit of bit/symbol. This choice is also consistent with

the fact that N = 2

equiprobable symbols, i.e., with probability 1/N = 1/2

, can be

represented by log

= q bits, meaning that all symbols from this source are made of

exactly q bits. In this case, there is no difference between the source entropy, H = q,the

symbol information, I = q, and the symbol bit length, l = q. In the rest of this book, it

will be implicitly assumed that the logarithm is of base two.

Let us illustrate next the source-entropy concept and its properties through practical

examples based on various dice games and even more interestingly, on our language.

4.2 Entropy in dice

Here we will consider dice games, and see through different examples the relation

between entropy and information. For a single die roll, the six outcomes are equiprob-

able with probability p(x) = 1/6. As a straightforward application of the deﬁnition, or

Eq. (4.7), the source entropy is thus (base-2 logarithm implicit):

H =−



i=1

log

≡ log 6 = 2.584 bit/symbol. (4.8)

We also have for the information: I = log 6 = 2.584 bits. This result means that it takes

3 bits (as the nearest upper integer) to describe any of the die-roll outcomes with the

same symbol length, i.e., in binary representation:

x = 1 → x100 x = 2 → x010 x = 3 → x110

x = 4 → x001, x = 5 → x101, x = 6 → x011,

54 Entropy

Table 4.1 Calculation of entropy associated with the result of rolling two dice. The columns show the

different possibilities of obtaining values from 2 to 12, the corresponding probability p and the product

−p log

p whose summation (bottom) is the source entropy H, which is equal here to 3.274 bit/

symbol.

Sum of dice numbers Probability (p) −p log

(p)

2 = 1 + 1 0.027 777 778 0.143 609 03

3 = 1 + 2 = 2 + 1 0.055 555 556 0.231 662 5

4 = 2 + 2 = 3 + 1 = 1 + 3 0.083 333 333 0.298 746 88

5 = 4 + 1 = 1 + 4 = 3 + 2 = 2 + 3 0.111 111 111 0.352 213 89

6 = 5 + 1 = 1 + 5 = 4 + 2 = 2 + 4 = 3 + 3 0.138 888 889 0.395 555 13

7 = 6 + 1 = 1 + 6 = 5 + 2 = 2 + 5 = 4 + 3 = 3 + 4 0.166 666 667 0.430 827 08

8 = 6 + 2 = 2 + 6 = 5 + 3 = 3 + 5 = 4 + 4 0.138 888 889 0.395 555 13

9 = 6 + 3 = 3 + 6 = 5 + 4 = 4 + 5 0.111 111 111 0.352 213 89

10 = 6 + 4 = 4 + 6 = 5 + 5 0.083 333 333 0.298 746 88

11 = 6 + 5 = 5 + 6 0.055 555 556 0.231 662 5

12 = 6 + 6 0.027 777 778 0.143 609 03



= 1.

Source entropy



= 3.274.

where the ﬁrst bit x is zero for all six outcomes. Nothing obliges us to attribute to each

outcome its corresponding binary value. We might as well adopt any arbitrary 3-bit

mapping such as:

x = 1 → 100 x = 2 → 010 x = 3 → 110

x = 4 → 001, x = 5 → 101, x = 6 → 011.

The above example illustrates a case where entropy and symbol information are equal,

owing to the equiprobability property. The following examples illustrate the more general

case, highlighting the difference between entropy and information.

Two-dice roll

The game consists in adding the spots obtained from rolling two dice. The minimum

result is x = 2(= 1 + 1) and the maximum is x = 12 (= 6 + 6), corresponding

to the event space X =

{

2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12

}

. The probability distribution

p(x) was described in Chapter 1, see Figs. 1.1 and 1.2. Table 4.1 details the 11 differ-

ent event possibilities and their respective probabilities p(x). The table illustrates that

there exist 36 equiprobable dice-arrangement outcomes, giving ﬁrst p(1) = p(12) =

1/36 = 0.027. The probability increases for all other arrangements up to a maximum

corresponding to the event x = 7 with p(7) = 6/36 = 0.166. Summing up the values

of −p(x)log p(x), the source entropy is found to be H = 3.274 bit/symbol. This result

shows that, on average, the event can be described through a number of bits between 3

and 4. This was expected since the source has 11 elements, which requires a maximum

of 2

= 4 bits, while most of the events (namely, x = 2, 3, 4, 5, 6, 7, 8, 9) can be coded

4.2 Entropy in dice 55

in principle with only 2

=3 bits. The issue of ﬁnding the best code to attribute a symbol

of minimal length to each of the events will be addressed later.

The 421

The dice game called 421 for short was popular in last century’s French caf

es. The

game uses three dice and the winning roll is where the numbers 4, 2, and 1 show up,

regardless of order. The interest of this example is to illustrate Shannon’s property (3),

which is described in the previous section and also in Appendix B. The probability

of obtaining x = 4, 2, 1, like any speciﬁc combination where the three numbers are

different, is p(421) = (1/6)(1/6)(1/6) ×3! = 1/36 = 0.0277 (each die face has 1/6

chance and there are 3! possible dice permutations). The probability of winning is, thus,

close to 3%, which (interestingly enough) is strictly equal to that of the double six winner

(p(66) = (1/6)(1/6) = 1/36) in many other games using dice. The odds on missing a

4, 2, 1 roll are p(other) = 1 − p(421) = 35/36 = 0.972. A straightforward calculation

of the source entropy gives:

H(421, other) =−p(421) log

p(421) − [1 − p(421)] log

[1 − p(421)]

(4.9)

log

36 +

log

≡ 0.183 bit/symbol.

The result shows that for certain sources, the average information is not only a real

number involving “fractions” of bits (as we have seen), but also a number that can

be substantially smaller than a single bit! This intriguing feature will be clariﬁed in a

following chapter describing coding and coding optimality.

Next, I shall illustrate Shannon’s property (3) based on this example. What we did

consisted in partitioning all possible events (result of dice rolls) into two subcate-

gories, namely, winning (x = 4, 2, 1) and losing (x = other), which led to the entropy

H = 0.183 bit/symbol. Consider now all dice-roll possibilities, which are equiprobable.

The total number of possibilities (regardless of degeneracy) is N = 6 × 6 ×6 = 216,

each of which is associated with a probability p = 1/216. The corresponding informa-

tion is, by deﬁnition, I (216) = log 216 = 7.7548 bits.

We now make a partition between the winning and the losing events. This gives

n(421) = 3! = 6, and n(other) = 216 −6 = 210. According to Shannon’s rule (3), and

following Eq. (B17) of Appendix B, we have:

I (N) = H

(

, p

)

+ p

I (n

) + p

I (n

)

= H

(

421, other

)

+ p(421)I [n(421)] + p(other)I [n(other)]

= 0.1831 + (1/36)I (6) +(35/36)I (210) = 0.1831 +0.0718 +7.4999

≡ 7.7548 bits, (4.10)

which is the expected result.

One could argue that there was no real point in making the above veriﬁcation, since

property (3) is ingrained in the entropy deﬁnition. This observation is correct: the

exercise was simply meant to illustrate that the property works through a practical

56 Entropy

example. Yet, as we shall see, we can take advantage of property (3) to make the rules

more complex and exciting, when introducing further “winning” subgroups of interest.

For instance, we could keep “4, 2, 1” as the top winner of the 421 game, but attribute 10

bonus points for any different dice-roll result mnp in which m + n + p = 7. Such a rule

modiﬁcation creates a new partition within the subgroup we initially called “other.” Let’s

then decompose “other” into “bonus” and “null,” which gives the source information

decomposition:

I (N) = H

(

421, bonus, null

)

+ p(421)I [n(421)]

(4.11)

+ p(bonus)I [n(bonus)] + p(null)I [n(null)].

The reader can easily establish that there exists only n(bonus) = 9 possibilities for the

“bonus” subgroup (which, to recall, excludes any of the “421” cases), thus p(bonus) =

9/216, and p(null) = 1 − p(421) − p(bonus) = 1 − 1/36 −9/216 =0.9305 (this alter-

native rule of the 421 game gives about 7% chances of winning something, which more

than doubles the earlier 3% and increases the excitement). We obtain the corresponding

source entropy;

(

421, bonus, null

)

=−p(421) log

[p(421)] − p(bonus) log

[p(bonus)] − p(null) log

[p(null)]

≡ 0.4313 bit/symbol. (4.12)

We observe that the entropy H

(

421, bonus, null

)

≡ 0.4313 bit/symbol is more than the

double of H(421, other) = 0.183 bit/symbol, a feature that indicates that the new game

has more diversity in outcomes, which corresponds to a greater number of “exciting”

possibilities, while the information of the game, I (N ), remains unchanged. Thus, entropy

can be viewed as representing a measure of game “excitement,” while in contrast infor-

mation is a global measure of game “surprise,” which is not the same notion. Consider,

indeed, two extreme possibilities for games:

Game A: the probability of winning is very high, e.g., p

(win) = 90%;

Game B: the probability of winning is very low, e.g., p

(win) = 0.000 01%.

One easily computes the game entropies and information:

H(A) = 0.468 bit/symbol I

win

(A) = 0.152 bit,

H(B) = 0.000 002 5 bit/symbol I

win

(B) = 23.2 bit.

We observe that, comparatively, game A has signiﬁcant entropy and low information,

while the reverse applies to game B. Game A is more exciting to play because the player

wins much more often, hence a high entropy (but low information). Game B has more

of a surprise potential because of the low chances of winning, hence a high information

(but low entropy).